Abstract
The discovery of magnetism in carbon structures containing zigzag edges has stimulated new directions in the development and design of spintronic devices. However, many of the proposed structures are designed without incorporating a key phenomenon known as topological frustration, which leads to localized non-bonding states (free radicals), increasing chemical reactivity and instability. By applying graph theory, we demonstrate that topological frustrations can be avoided while simultaneously preserving spin ordering, thus providing alternative spintronic designs. Using tight-binding calculations, we show that all original functionality is not only maintained but also enhanced, resulting in the theoretically highest performing devices in the literature today. Furthermore, it is shown that eliminating armchair regions between zigzag edges significantly improves spintronic properties such as magnetic coupling.
Similar content being viewed by others
Introduction
Carbon-based spintronics is an exciting topic with vast potential, most notably in fast memory devices, logic gates, transistors and capacitors for computers, tablets and hand-held devices1,2,3. This is a very attractive alternative to existing technologies because the synthesis and processing of carbon-based nanostructures can be relatively inexpensive and easy. Furthermore, all-hydrocarbon products can significantly reduce the need for critical materials used by the semi-conductor industry (e.g., indium and gallium). Realizing this potential requires an understanding of the origins of magnetic coupling and improvement of this key property, enabling the design of new and significantly enhanced spintronic devices. In this paper we focus on magnetic coupling and uncover simple structural rules derived from graph theory that lead to enriched structure/property relationships.
Zigzag edges in sp2 carbon have demonstrated spin ordered properties in such structures as graphene nanoribbons (with bases of graphene4,5 and coronene6), open nanotubes7, nanowiggles8, nanorings9,10,11, nanomeshes12, nanodots13 and many more14,15. While each of these individual structures have interesting properties, spin alignment between graphene layers can become coupled, allowing for more complicated device designs16. Simulations have demonstrated that external magnetic fields can change the spin ordering on zigzag edges17 and even static electric fields might have the potential to influence the spin properties of nanostructured carbon18,19. Carbon chain links have been proposed as another method of transferring spin information between flakes20 and theoretical studies using metal contacts and side groups have been published21,22.
However, the current literature on structural design often fails to recognize the existence of topological frustration, a frequent property of such devices that greatly decreases the likelihood of their experimental realization. Topological frustration occurs when all pz orbitals cannot form p bonds in sp2 hybridized carbon due to topological reasons, leading to open electronic shells23. In classical chemistry, these structures cannot possess a complete Kekulé structure, as every sp2 carbon is not double bonded exactly once, leading to free radical formation. These are considered non-Kekuléan (or “concealed”) structures24.
Attempts at synthesis of non-Kekuléan hydrocarbon structures have resulted in unstable structures that decay at ambient conditions, destroying the desired properties at room temperature25 or that oxidize in a few days when exposed to ambient atmosphere26. Stable non-Kekulé structures exist but generally require the introduction of non-carbon atoms27,28. While new methods for producing carbon nanostructures with spintronic properties and exacting edge designs are still being proposed29 or experimentally realized30, much of the current literature is generally unaware of the adverse effects of topological frustration in the final structures.
To the best of our knowledge, Wang et al. were the first to use the specific term “topological frustration” in reference to graphene nanoflakes (GNFs) with spintronic properties14. Our definition is slightly different from that of Wang et al., as they considered particular classes of structures frustrated if there existed a topologically frustrated substructure31. This definition is not easily quantifiable because it requires arbitrarily defined substructures that cannot always be easily identified. Our definition considers the entire structure allowing it to be mathematically quantifiable via graph theory.
Until very recently, topological frustration was thought of as a binary operator: either a molecule is frustrated or it isn't. It has been demonstrated that this phenomenon can be quantified in units of “topological frustrations,” and each frustration yields a free radical, making the system progressively more energetically unfavorable32. In terms of graph theory, the number of topological frustrations is the number of uncovered nodes in the maximal graph G of a structure, provided G is constructed from V nodes correlated to sp2 carbon atoms and E edges being the covalent bonds between said atoms. Additionally, by enumerating over all possible maximal matchings, all possible locations of the free radicals can be discovered, thus revealing critical information on delocalization of the system.
Existing carbon-based designs
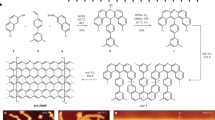
One popular, yet topologically frustrated, family of structures in the field of carbon spintronics is that of the triangular zigzag graphene nanoflake (TZGNF, sometimes referred to as triangulene, see Figure 1 (a)). TZGNFs are all-hydrocarbon ferromagnets, a consequence of having sublattices with unequal spins that produces a net spin, in agreement with Lieb's theorem33. TZGNFs have been investigated for potential use as optoelectronic34 and logic devices31, or as spin filters whose properties scale with increasing flake size35. However, TZGNFs possess the mathematical property of having a number of topological frustrations equal to the number of benzene rings on one side of the triangle minus one, which explains the scaling of the spin filter properties with increasing flake size.
(a) Kekulé structure of a triangular zigzag graphene nanoflake (TZGNF). No matter how the double bonds are arranged, at least two atoms will always be lacking a double bond, leading to the creation of free radicals (or topological frustrations, in this case two). This phenomenon can be quantified with a concept borrowed from graph theory known as maximal matching. (b) Bow-tie graphene nanoflake, or Clar's goblet. Note that the topological frustrations can exist on the interior or the edge atoms (as long as they belong to the given sublattice, for the structures presented here) and there are many more arrangements of the Kekulé structure possible. (c) If we connect the TZGNF from (a) with its mirror image, we arrive at structure (c) which has no topological frustration. The free radicals were able to recombine and form stable double bonds.
Bow-tie graphene nanoflakes, also known as Clar's goblet (Figure 1 (b)), constitute another class of popular structures17. Bow-ties have been predicted to show potential application as spin filters or as switches36,37. Interestingly, most possess topological frustrations, with the quantity depending on geometrical properties such as the length of the sides and width of the neck region.
The destabilizing effects of topological frustrations and the presence of free radicals on the proposed TZGNF and bow-tie based devices are rarely, if ever, mentioned, despite the well-documented experimental difficulties of isolating such structures25,38. However, topological frustration is not a prerequisite for spin ordering and by careful device design their detrimental effects can be avoided. One method is to connect structures together in such a way that topological frustrations can become neighbors and annihilate each other. This process is synonymous with free radicals combining into p bonds. An example of this can be seen in Figure 1 (c). While this seems like a simple method to avoid the presence of free radicals, care must be taken that the connected atoms can be the sites of a topological frustration in at least some maximal resonance structure and that the total number of such connections is sufficient to annihilate all the frustrations. A graph theoretical based discussion of the rules of frustration annihilation can be found in the recent literature32.
Magnetic coupling
For the spintronic systems presented in this paper the most important functional property is magnetic coupling. Generally, magnetic coupling is the smallest difference in energy between spin ordered states used in the logical execution of the device. For the two-terminal NOT gates studied here, magnetic coupling is the difference in energy between the ferromagnetic (FM) and antiferromagnetic (AFM) spin states. The total energy of the non-polarized state should be found as well, but it is not presented here as it is usually so energetically unfavorable as to have no bearing on the determination of the properties of the system. Note that for four-terminal NOT OR (NOR) gates or NOT AND (NAND) gates, other possible stable ordered states besides the FM and AFM spin configurations are possible.
Table 1 shows example calculations for determining the magnetic coupling of four-terminal NOR and NAND gates, using the demonstration structures in Figure 2. For a symmetric gate, the energies of five distinct spin orderings must be found (including the non-magnetic state). While only symmetric gates are presented here, asymmetric gates would require finding the energies of up to eight spin ordered states, which can be obtained by simple combinatorics and consideration of up-down spin symmetry.
 . The magnetic couplings can be deduced from the data presented, for structure (a) it is 93 meV and for (b) it is 113 meV. Also note the redundancy in the energies listed due to the rotational symmetry of the structures
. The magnetic couplings can be deduced from the data presented, for structure (a) it is 93 meV and for (b) it is 113 meV. Also note the redundancy in the energies listed due to the rotational symmetry of the structuresExample spintronic logic gate devices constructed from carbon.
A demonstration calculation for finding the magnetic coupling of each is presented in Table 1. The regions labeled A and B are the inputs, while D is the output and C is a programmable bit. Devices (a) and (b) each can function as NOR or NAND gates, depending on the value of the programmable bit. Both devices also have valid Kekulé structures (no topological frustrations or free radicals) and both have the highest magnetic coupling values of their respective families (demonstrated in Figure 3).
Thermal fluctuations can randomly flip spin orientation, which interferes with the operation of spin-logic devices. However, as long as the device is accurate at least 50% of the time it is possible to deduce the correct state using schemes such as time averaging, or averaging the values of several devices. An estimate of the minimum spin-flip energy necessary for device operation can be obtained from Néel relaxation theory in the absence of a magnetic field via the Néel-Arrhenius equation39,

where τN is the average amount of time for a nanoparticle's magnetization to randomly flip due to thermal fluctuations and τ0 is the switching time. ΔE is the kinetic energy barrier for flipping the spin, kB is the Boltzmann constant and T is the temperature. At room temperature (T = 300 K), the magnetic coupling energy is equal to40, ΔE = −kBTln(0.5) = 18 meV.
In this paper, we propose several design variants of popular devices that have magnetic couplings on-par with or better than those reported in the literature today and yet are more stable and less reactive due to having a Kekuléan type structure. In addition, we demonstrate the strengthening of spintronic properties by the elimination of armchair regions between zigzag edges.
Kekuléan logic gate structures
The first family of carbon logic structures we will improve upon is that of NOT gates, most commonly implemented from bow-tie GNFs. Using the previously mentioned rules of frustration annihilation, we choose TZGNFs as building blocks: by knowing that topological frustrations for TZGNFs can reside on the edge atoms, frustrations can be eliminated by connecting such edge atoms across flakes. This construction leads to a structure like that in Figure 1 (c) or Figure 3 (a). The TZGNFs on each side must be of the same size to prevent frustration. Thus structural index n is the number of benzene rings on one side of one of the TZGNFs.
Structure and magnetic couplings vs. structure index for (a) TZGNF-based NOT gate (b) RGNF-based NOT gate (c) TZGNF-based NOR/NAND gate and (d) armchair-less TZGNF-based NOR/NAND gate.
In the example structure images the structure index n is three. Up spin on-site occupation is in blue, down spin occupation in red and half/half up/down occupation in white. It is apparent that the majority of the spin polarization occurs on the zigzag edges. Note that the axis scaling is different between the NOT and NOR/NAND gates. The best performing device for each structure family have magnetic couplings of: (a) 135 meV (b) 179 meV (c) 93 meV and (d) 113 meV, well above the 18 meV bare minimum threshold imposed by thermal fluctuations at room temperature (denoted as an orange horizontal line).
Additionally, we test a variant of this NOT gate that lacks the connecting armchair regions (Figure 3 (b)). This rhombus GNF (RGNF) is still Kekuléan and the reading and writing of spin information to such RGNFs has been theoretically demonstrated41, including an analysis of the structural properties42. By comparing these two structure families, we will see that not only are non-frustrated NOT gates viable, but we can also improve the magnetic coupling by keeping the connecting edges as zigzaged as possible.
The second family of carbon logic structures to be addressed are four-terminal gates, which can be programmed to function as NOR/NAND gates. We again use the method of TZGNF subunits to construct structures like that found in Figure 3 (c). If we consider a rotationally symmetric gate with side TZGNF terminals that have a length of n benzene rings, using the rules of frustration annihilation we can derive that the central TZGNF must be of a length m = 3(n − 1) + 1 to avoid topological frustration. Thus n is the only independent variable. It should be noted that the total structure does not necessarily need to be rotationally symmetric to function as a logic gate, however, for simplicity we restrict ourselves to this situation.
Once again we test a variant of this proposed logic structure by eliminating the armchair regions, as seen in Figure 3 (d). In this instance, the rules of frustration annihilation dictate that for n benzene rings on the side terminals, the central TZGNF must have a length m = 3 × n + 1.
The magnetic coupling energy as a function of the structural index n for these four different families are presented in Figure 3. Many trends are apparent, but the most important one is that every structure with a non-zero magnetic coupling features a coupling strength above the critical threshold of 18 meV. This confirms that structures without topological frustration can still maintain spintronic properties appropriate for device functionality, while still preserving all the benefits of a stable Kekulé structure. Thus there is no drawback to these alternative designs. In fact, our highest performing NOT logical gates have magnetic couplings similar to, or greater than, that of the current literature and our NOR/NAND gates outperform those in the literature by a factor of two to three31.
A second trend worth noting is the effect of eliminating armchair edges. It is difficult to directly compare any two structures from different families; a fair comparison to judge which design is better for magnetic coupling would require each structure to have the same number of edge and interior atoms. Another consideration is that there are structures in each family with magnetic couplings that lie between the highest and the lowest values of the other families.
As the structure index approaches large values, the magnetic coupling oscillates with decreasing amplitude about a baseline value. This can be seen as a consequence of approaching the limit of coupling between two spin ordered edges as they move further away from each other. Thus the largest magnetic coupling values are found in the relatively small flakes and by comparing the best values between like families with and without connecting armchair regions, it is readily apparent that keeping the functional areas connected by zigzag edges increases performance by at least 20%. An additional method to show that junctions of pure zigzag edges are superior is to compare the apparent large-scale GNF baseline values: the armchair-less families trend higher in the large-scale limit than the armchair ones.
Discussion
We identified that several carbon nanostructures with exciting spintronic properties are unstable due to the presence of topological frustrations. Using the rules of frustration annihilation, we demonstrate alternative designs with no topological frustrations for a number of NOT, NOR and NAND logic gates with spintronic properties that are not only maintained, but also strengthened. This is a significant improvement, since removing the topological frustrations also eliminates the presence of free radicals. This leads to easier fabrication and less reactivity in ambient conditions.
In addition to improving stability, we also augmented the functional property of magnetic coupling by structural design choices alone. This was achieved by minimizing or eliminating the use of armchair corners connecting zigzag edges, which produced a significant increase in magnetic coupling. We were also able to identify new structures whose magnetic and spintronic properties exceeds the best published in the literature today.
Finally, as shown in the Method Section, the use of tight-binding as a method for characterizing the spintronic properties of carbon has been verified by comparing results from density functional theory. Tight-binding enables rapid simulations in a fraction of the computational time associated with density functional theory, thus providing a fast and accurate technique for the guided design of new carbon based spintronic nanostructures for potential use in the digital industry.
Methods
Density functional theory (DFT) calculations have been used successfully to assess the electronic and magnetic properties of carbon-based nanomaterials. However, in order to allow for the fast prototyping of materials for spintronic logical gate systems, a high throughput methodology is needed. Here, we show that a model Hamiltonian approach based on a tight-binding (TB) description of the electronic properties (when augmented with an on-site Hubbard-like repulsion term, U) leads to quantitative results that are orders of magnitude faster than DFT type approaches. This provides a fast and accurate approach for rapid prototyping of carbon based spintronic nanostructures and its associated data for other materials genome type activities.
To demonstrate the reliability of the TB + U model, we systematically compared the magnetic coupling constants (i.e., for carbon NOT gates, the difference between the energy of the AFM and FM spin states) obtained from TB + U against those obtained with the DFT based methods. These simulations were performed on a variety of graphene nanoflakes that are selected from a set of 32 systems, studied originally by Wang et al.31 (Figure 4).
Left: the two classes of graphene nanoflakes considered for benchmarking purposes. The indices n and m correspond to the shape of the points on each line in the energy plots. Right: magnetic couplings computed using TB + U and VASP as a function of index n. In these plots, the different symbols correspond to m = 1 ( ), m = 2 (
), m = 2 ( ), m = 3 (
), m = 3 ( ), m = 4 (
), m = 4 ( ). Colors used for data on the right correspond to the colored structures on the left.
). Colors used for data on the right correspond to the colored structures on the left.
The DFT calculations presented here were performed with the Vienna Ab-Initio Simulation Package (VASP), which employs a plane-wave basis set43,44, while Wang et al. studied the same structures by using a numerical atomic basis set within the SIESTA code45. The coordinates of all structures were relaxed via conjugate gradient minimization until the maximum force on each atom was less than 0.01 eV Å−1 and the total energy convergence was determined when the difference in energy between consecutive self-consistent iterations was ΔE < 10−8 eV. The Perdew-Burke-Ernzerhof generalized gradient approximation DFT functional and the projected augmented wave (PAW) pseudopotentials46,47,48,49 were used. A plane-wave cutoff energy of 450 eV was determined to yield converged energies. As these nanoflakes are non-periodic, only Γ-point sampling of the Brillouin zone was necessary. Standard FM and AFM spin configurations were considered. In the VASP calculations, as well as in Wang's work31, the edges of the nanoflakes were passivated with hydrogen atoms to increase thermodynamic stability50.
The TB + U calculations are based on the following Hamiltonian, expressed in second quantization as,

with


H0 is the usual TB Hamiltonian and  the annihilation (creation) operator for an electron on site i with spin σ. The sum is performed over pairs of first-, second- and third-neighbor sites. Here,
the annihilation (creation) operator for an electron on site i with spin σ. The sum is performed over pairs of first-, second- and third-neighbor sites. Here,  is the hopping integral between sites i and j and we consider hopping interactions up to third-neighbor sites. The hopping integrals for the first-, second- and third-neighbors are given by tij = 3.2, tij = 0 and tij = 0.3 eV, respectively51. In addition, we use a Δtij = 0.2 eV correction on the first-neighbor hopping for the frontier atoms to account for the different chemical environments at the edges51. Electron-electron interactions include an approximate treatment based on the Hubbard term HU. Its mean field expression is
is the hopping integral between sites i and j and we consider hopping interactions up to third-neighbor sites. The hopping integrals for the first-, second- and third-neighbors are given by tij = 3.2, tij = 0 and tij = 0.3 eV, respectively51. In addition, we use a Δtij = 0.2 eV correction on the first-neighbor hopping for the frontier atoms to account for the different chemical environments at the edges51. Electron-electron interactions include an approximate treatment based on the Hubbard term HU. Its mean field expression is

where  is the number operator and U is the on-site repulsion, given by U = 2.944 eV8. Here, the occupations are determined self-consistently. Once convergence is achieved, the TBU band structure energy is calculated using
is the number operator and U is the on-site repulsion, given by U = 2.944 eV8. Here, the occupations are determined self-consistently. Once convergence is achieved, the TBU band structure energy is calculated using

where n(E) = n↑(E) + n↓(E) is the total density of states and EF is the Fermi energy. The second term on the right in Eq. (6) is introduced to correct double-counting of the electron-electron repulsion in the TB + U band-structure energy calculation.
Figure 4 (left) shows the structure of the graphene nanoflakes considered in our benchmark calculations. The parameter m represents the width of the joint of the intersection of two flakes; n is the width of the flakes. The red and blue structures differ by an offset of the joint.
The results of the magnetic coupling calculations using the two different methods are also shown in Figure 4. Inspection of the plots clearly shows an excellent quantitative agreement between TB + U and DFT. We note some discrepancy between the SIESTA results from reference 31 and our VASP results, due to basis set incompleteness from the former. SIESTA uses a pseudo-atomic orbital basis set45, whereas VASP uses a plane-wave basis set which has spectral convergence properties meaning that the result systematically converges by increasing the plane-wave basis set. This is not true when using numerical pseudo-atomic orbital basis set as employed in SIESTA. We observe that the TB + U scheme produces accurate predictions of the magnetic coupling of well-established benchmark systems when compared to first-principles, plane-wave DFT and thus, is capable of making reliable quantitative predictions on the magnetic coupling of carbon nanostructures considered in this paper.
References
Naber, W., Faez, S. & Van der Wiel, W. Organic spintronics. J. Phys. D: Appl. Phys. 40, R205 (2007).
Chen, P. & Zhang, G. Carbon-based spintronics. Sci. China Phys. Mech. Astron. 56, 207–221 (2013).
Kuemmeth, F., Churchill, H. O. H., Herring, P. K. & Marcus, C. M. Carbon nanotubes for coherent spintronics. Mater. Today 13, 18–26 (2010).
Dutta, S. & Pati, S. K. Novel properties of graphene nanoribbons: a review. J. Mater. Chem. 20, 8207–8223 (2010).
Daniels, C., Bullard, Z., Gi[rtilde]ao, E. C. & Meunier, V. Emergent magnetism in irradiated graphene nanostructures. Carbon 78, 196–203 (2014).
de Aguiar, A. L. et al. Electronic and magnetic structures of coronene-based graphitic nanoribbons. Phys. Chem. Chem. Phys. 16, 3603–3609 (2014).
Huang, B. et al. Multiple localized states and magnetic orderings in partially open zigzag carbon nanotube superlattices: An ab initio study. J. Chem. Phys 133, 084702 (2010).
Costa Girão, E., Liang, L., Cruz-Silva, E., Filho, A. G. S. & Meunier, V. Emergence of atypical properties in assembled graphene nanoribbons. Phys. Rev. Lett. 107, 135501 (2011).
Potasz, P., Güçlü, A. & Hawrylak, P. Spin and electronic correlations in gated graphene quantum rings. Phys. Rev. B 82, 1–7 (2010).
Potasz, P., Güçlü, A., Voznyy, O., Folk, J. & Hawrylak, P. Electronic and magnetic properties of triangular graphene quantum rings. Phys. Rev. B 83, 174441 (2011).
Grujić, M., Tadić, M. & Peeters, F. Antiferromagnetism in hexagonal graphene structures: Rings versus dots. Phys. Rev. B 87, 085434 (2013).
Yang, H.-X., Chshiev, M., Boukhvalov, D. W., Waintal, X. & Roche, S. Inducing and optimizing magnetism in graphene nanomeshes. Phys. Rev. B 84, 214404 (2011).
Hod, O., Barone, V. & Scuseria, G. E. Half-metallic graphene nanodots: A comprehensive first-principles theoretical study. Phys. Rev. B 77, 035411 (2008).
Wang, W. L., Meng, S. & Kaxiras, E. Graphene nanoflakes with large spin. Nano Lett. 8, 241–245 (2008).
Yazyev, O. V. Emergence of magnetism in graphene materials and nanostructures. Rep. Prog. Phys. 73, 056501 (2010).
Guinea, F. Spin–orbit coupling in a graphene bilayer and in graphite. New J. Phys. 12, 083063 (2010).
Szałowski, K. Ground-state magnetic phase diagram of bow-tie graphene nanoflakes in external magnetic field. J. Appl. Phys. 114, 243908 (2013).
Son, Y.-W., Cohen, M. L. & Louie, S. G. Half-metallic graphene nanoribbons. Nature 444, 347–349 (2006).
Sheng, W., Luo, K. & Zhou, A. Electric field induced spin polarization in graphene nanodots. Phys. Rev. B 90, 085406 (2014).
Zhou, J., Wang, Q., Sun, Q. & Jena, P. Intrinsic ferromagnetism in twodimensional carbon structures: triangular graphene nanoflakes linked by carbon chains. Phys. Rev. B 84, 081402 (2011).
Deng, X., Tang, G. & Guo, C. Tuning the electronic transport properties for a trigonal graphene flake. Phys. Lett. A 376, 1839–1844 (2012).
Zhang, J. et al. Enhanced half-metallicity in carbon-chain–linked trigonal graphene. Org. Electron. 15, 65–70 (2014).
Longuethiggins, H. Some studies in molecular orbital theory i resonance structures and molecular orbitals in unsaturated hydrocarbons. J. Chem. Phys. 18, 265–274 (1950).
Randic, M. Aromaticity of polycyclic conjugated hydrocarbons. Chem. Rev. 103, 3449–3606 (2003).
Inoue, J. et al. The first detection of a clar's hydrocarbon, 2, 6, 10-tritert-butyltriangulene: A ground-state triplet of non-kekulé polynuclear benzenoid hydrocarbon. J. Am. Chem. Soc. 123, 12702–12703 (2001).
Tukada, H. & Mutai, K. A stable triplet non-kekulé molecule; m-phenylene-2, 2-bis (1, 1: 3, 3-di-2, 2-biphenylenepropenyl). Tetrahedron Lett. 33, 6665–6668 (1992).
Koide, T. et al. A stable non-kekulé singlet biradicaloid from meso-free 5,10,20,25-tetrakis(pentafluorophenyl)-substituted [26]hexaphyrin(1.1.1.1.1.1). J. Am. Chem. Soc. 132, 7246–7247 (2010).
Ueda, A. et al. An extremely redox-active air-stable neutral π radical: Dicyanomethylene-substituted triangulene with a threefold symmetry. Chem. Eur. J. 18, 16272–16276 (2012).
Gao, X. et al. Oxidation unzipping of stable nanographenes into joint spinrich fragments. J. Am. Chem. Soc. 131, 9663–9669 (2009).
Campos, L. C., Manfrinato, V. R., Sanchez-Yamagishi, J. D., Kong, J. & Jarillo-Herrero, P. Anisotropic etching and nanoribbon formation in singlelayer graphene. Nano Lett. 9, 2600–2604 (2009).
Wang, W. L., Yazyev, O. V., Meng, S. & Kaxiras, E. Topological frustration in graphene nanoflakes: Magnetic order and spin logic devices. Phys. Rev. Lett. 102, 157201 (2009).
Bullard, Z., Costa Girão, E., Daniels, C., Sumpter, B. G. & Meunier, V. Quantifying energetics of topological frustration in carbon nanostructures. Phys. Rev. B 89, 245425 (2014).
Lieb, E. H. Two theorems on the hubbard model. Phys. Rev. Lett. 62, 1201–1204 (1989).
Ghaffarian, M. & Ebrahimi, F. The linear and nonlinear optical properties of trigonal zigzag graphene nanoflakes. Phys. Scr. 88, 025703 (2013).
Sheng, W., Ning, Z. Y., Yang, Z. Q. & Guo, H. Magnetism and perfect spin filtering effect in graphene nanoflakes. Nanotechnology 21 (2010).
Kang, J., Wu, F. & Li, J. Spin filter and molecular switch based on bowtieshaped graphene nanoflake. J. Appl. Phys. 112, 104328 (2012).
Li, J., Zhang, Z., Zhang, J. & Deng, X. Rectifying regularity for a combined nanostructure of two trigonal graphenes with different edge modifications. Org. Electron. 13, 2257–2263 (2012).
Clar, E., Kemp, W. & Stewart, D. The significance of kekulé structures for the stability of aromatic systems. Tetrahedron 3, 325–333 (1958).
Néel, L. Théorie du traînage magnétique des ferromagnétiques en grains fins avec applications aux terres cuites. Ann. géophys 5, 99–136 (1949).
Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 5, 183–191 (1961).
Agapito, L. A., Kioussis, N. & Kaxiras, E. Electric-field control of magnetism in graphene quantum dots: Ab initio calculations. Phys. Rev. B 82, 201411 (2010).
Bera, S., Arnold, A., Evers, F., Narayanan, R. & Wölfle, P. Elastic properties of graphene flakes: Boundary effects and lattice vibrations. Phys. Rev. B 82, 195445 (2010).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio totalenergy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Soler, J. M. et al. The siesta method for ab initio order-n materials simulation. J. Phys.: Condens. Matter 14, 2745 (2002).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Errata for generalized gradient approximation made simple [phys. rev. lett. 77, 3865 (1996)]. Phys. Rev. Lett. 78, 1396–1396 (1997).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Barone, V., Hod, O. & Scuseria, G. E. Electronic structure and stability of semiconducting graphene nanoribbons. Nano Lett. 6, 2748–2754 (2006).
Gunlycke, D. & White, C. T. Tight-binding energy dispersions of armchairedge graphene nanostrips. Phys. Rev. B 77, 115116 (2008).
Acknowledgements
This work was supported by the Office of Naval Research. Calculations were performed on the Center for Computational Innovations (CCI) at Rensselaer Polytechnic Institute. Portions of this research were conducted with high performance computational resources provided by Louisiana State University (http://www.hpc.lsu.edu).
E.C.G. acknowledges support from Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) (Process Number 473714/2013-2). E.C.G. and V.M. acknowledge support from Coordenação de Aperfeicoamento de Pessoal de Nível Superior (CAPES) through the Science Without Borders program (Project Number A085/2013).
Author information
Authors and Affiliations
Contributions
Z.B. designed the device structures and ran the tight-binding calculations. Z.B., E.G., J.O. and V.M. wrote the manuscript. E.G. coded the tight-binding implementation. Z.B., E.G. and J.O. made the figures. J.O. and W.S. performed benchmarking tests between tight binding and density functional theory simulations. V.M. managed the execution of the project. All authors critically reviewed the paper for revisions.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Bullard, Z., Girão, E., Owens, J. et al. Improved All-Carbon Spintronic Device Design. Sci Rep 5, 7634 (2015). https://doi.org/10.1038/srep07634
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07634
This article is cited by
-
Spin splitting of dopant edge state in magnetic zigzag graphene nanoribbons
Nature (2021)
-
Existence of multi-radical and closed-shell semiconducting states in post-graphene organic Dirac materials
Nature Communications (2017)
-
Synthesis and characterization of triangulene
Nature Nanotechnology (2017)
-
Structural Asymmetry-Facilitated Tunability of Spin Distribution in the (10, 0) Carbon Nanotube Induced by Charging
Journal of Electronic Materials (2017)
-
Slippage in stacking of graphene nanofragments induced by spin polarization
Scientific Reports (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.