Abstract
When a large set of discrete bodies passes through a bottleneck, the flow may become intermittent due to the development of clogs that obstruct the constriction. Clogging is observed, for instance, in colloidal suspensions, granular materials and crowd swarming, where consequences may be dramatic. Despite its ubiquity, a general framework embracing research in such a wide variety of scenarios is still lacking. We show that in systems of very different nature and scale -including sheep herds, pedestrian crowds, assemblies of grains and colloids- the probability distribution of time lapses between the passages of consecutive bodies exhibits a power-law tail with an exponent that depends on the system condition. Consequently, we identify the transition to clogging in terms of the divergence of the average time lapse. Such a unified description allows us to put forward a qualitative clogging state diagram whose most conspicuous feature is the presence of a length scale qualitatively related to the presence of a finite size orifice. This approach helps to understand paradoxical phenomena, such as the faster-is-slower effect predicted for pedestrians evacuating a room and might become a starting point for researchers working in a wide variety of situations where clogging represents a hindrance.
Similar content being viewed by others
Introduction
Can it be taken for granted that an enclosure filled with particles could be emptied through a small opening in a finite time? It is an everyday experience that a saltcellar has to be shaken to break the clogging arches1 and pour the salt. Arches also cause flow interruptions in industrial conduits and silos. At smaller scales, the intermittent flow of a dense microparticle suspension can occlude microchannel constrictions2,3; this is exploited in medicine to provoke embolization of blood vessels in order to shrink a tumour. Intermittent flows are also observed at the nanoscale when electrons on the liquid helium surface pass through nanoconstrictions4. The most dramatic instance of clogging is a crowd trying to escape through a door in a life-and-death situation5,6,7. Human stampedes –some of them leading to a clog in narrow passages– often result in fatalities, such as those at Hillsborough Stadium (England), The Station nightclub (USA) and Kiss nightclub (Brazil). Here, we show that clogging in several disparate systems is amenable to a unified treatment. A careful analysis of experimental and numerical results in four different scenarios allows us to evidence the generality of the flow of many-particle systems through bottlenecks, revealing that clogging is linked to a particular characteristic of the intermittent flow.
Results
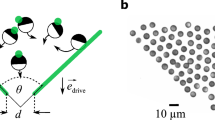
The first observation concerns the rush of sheep herds through a gate, to obtain food. An accurate timing of each animal crossing the door (Fig. 1B) is obtained by means of spatio-temporal diagrams as the one shown in Fig. 1C, built from videos taken on a farm (S1). We observe a characteristic alternation between events of sheep flow, or bursts, separated by periods of arrest, or clogs. The nature of this intermittent flow is also captured in the plot of the number of evacuated sheep versus time (Fig. 1D) where horizontal lines evidence clogs. The complementary cumulative distribution function (CDF) of the time lapses τ between the passage of consecutive sheep is then built, as displayed in Fig. 1E. The distribution has a power-law tail, τ−α, as observed before in other intermittent flows with mice8 and vibrated silos9. This slowly decaying probability indicates the existence of long time lapses in the flow. We use a rigorous method10 to fit the exponent α that also gives the minimum time lapse τmin from which the power law fit is valid. This τmin is used as a threshold to set apart successive bursts. The size of bursts s (measured in number of individuals) always displays an exponential distribution (Fig. 1F), as predicted theoretically11,12 and observed for the avalanches in granular silos13 and fluid-driven particle flow14. The flow of sheep can be altered, without changing the doorway, by placing a column in front of the door (Fig. 1A). In both cases (with and without column) burst sizes follow exponential distributions (so the average <s> is well defined) and the complementary CDF of time lapses displays power-law tails. Interestingly, the complementary CDF captures the sensitivity of the flow intermittencies to the presence of an obstacle. With the obstacle in place, the value of α is higher, which demonstrates its role in precluding long flow interruptions.
Sheep flow through a bottleneck.
(A) Picture taken near the gate in a test performed placing an obstacle in front of it. (B) Picture taken after the gate, with a green line marking the pixels used to build the spatio-temporal diagram. (C) Spatio-temporal diagram (time increases from bottom to top). The two horizontal yellow lines mark a long time lapse and the two horizontal blue lines a short time lapse; the meaning of “long” and “short” in this context is explained in the main text. A burst of size s = 17 spans from the green horizontal line to the lower yellow line. The upper yellow line defines the beginning of the next burst. (D) Number of evacuated sheep (#) versus time for several realizations. Horizontal segments correspond to time lapses during which no sheep crossed the green line shown in b. (E) Complementary CDF of the time lapses obtained with and without an obstacle in front of the gate. The continuous lines represent the power law fits with their exponent α, as given by the Clauset-Shalizi-Newman method10. (F) Histogram of burst sizes (s) rescaled by the average burst size (〈s〉) for the experiments with and without obstacle. The minimum lapse τmin used here to set apart bursts is 1 s. Although this choice affects the particular value of 〈s〉, the exponential tail of the distribution (continuous line in the figure) is unaffected. A straightforward calculation of the mean avalanche size gives 〈s〉 = 17 with an obstacle and 〈s〉 = 11 without an obstacle, an enhancement similar to that found in silos15.
Given the limited control of the variables affecting the flow of sheep, we have developed an alternative approach to explore a wider range of conditions. To this end, we have performed numerical simulations modelling the passage of pedestrians through a small door (Fig. 2). We find again exponential burst size distributions (Fig. 2B) and power law tails in the time lapse distributions (Fig. 2C–E). Changing the parameters that determine pedestrian behaviour, we observe important variations in the exponent α of the power law decay, which in some cases falls below 2. When α ≤ 2 the average time lapse between consecutive pedestrians diverges18 and so does the mean evacuation time. This implies that in this regime the average flow rate is not well defined, as it depends on the measuring time: as the measuring time increases, the average flow rate decreases and eventually vanishes. These observations have prompted us to propose as an order parameter the flowing parameter, Φ = 〈tf〉/(〈tc〉 + 〈tf〉), where 〈tf〉 is the average duration of the bursts and 〈tc〉 the average clog duration. Φ captures the clogging transition in the sense that it defines a state, but it cannot tell whether the orifice is flowing or not at a given time: a system in a clogged state can briefly release some outflow and an unclogged system can be blocked, but the obstruction will not persist. Since bursts have a finite average size and the flow is not interrupted within a burst by definition, it follows that Φ = 0 when 〈tc〉 diverges (α ≤ 2) and Φ > 0 when 〈tc〉 is finite (α > 2). Accordingly, we define that the system is in a clogged state when Φ = 0 and in an unclogged state when Φ > 0. In this latter case, the flow is intermittent if 0 < Φ < 1 and continuous if Φ = 1. Even if the clogging transition is identified when the mean clogging time diverges, as it has been done previously, the choice of the order parameter highlights the universality of the clogging transition, which is preceded by a regime of intermittent flow.
Pedestrian simulation.
Simulation of pedestrians evacuating a room using the Social Force Model3 plus a random force in the y-direction (perpendicular to the door) uniformly distributed in the interval [−θ, θ] inspired by the random force term used by Helbing and coworkers16,17. (A) Sketch of the simulated system where L is the size of the door. (B) Distribution of burst sizes (s) rescaled by the average burst size (〈s〉) for the simulation conditions displayed in (C). The lower limit used to define the bursts is t = 5 s. Although this choice affects the particular value of 〈s〉, the exponential tail of the distribution (dashed line in the figure) is unaffected. (C,D,E) Complementary CDFs of the time lapses obtained using different simulation parameters. The reference conditions are: pedestrian desired velocity vd = 6 m/s, random force in the y-direction θ = 10 kN and door size L = 1.0 m. In (c, d and e), we vary vd, θ and L, respectively. In Fig. (C–E) the continuous lines represent the power-law fits with exponent α, as given by the Clauset-Shalizi-Newman method10. The transition from α ≤ 2 (clogged system) to α > 2 (clog-free system) is observed in all the cases as the desired velocity is reduced and the random force or the door size are increased.
In Fig. 2C–E, a transition from clogged (Φ = 0, i.e. α ≤ 2) to unclogged states (Φ > 0, i.e. α > 2) is obtained by reducing the desired velocity of pedestrians (vd), by increasing the door size (L), or by increasing the random force exerted by the individuals in the direction perpendicular to the door (θ). The behaviour obtained by varying L and θ is somehow expected, while that encountered for vd might be the origin of the well known faster-is-slower phenomenon6.
In order to extend the generality of this behaviour to inert grains, we resorted to a series of experiments using three configurations of vibrated silos (Fig. 3). As observed for sheep and simulated pedestrians, the outcomes reveal exponential burst size distributions (not shown as they have been extensively studied in the literature9,11,12,13,14,15) and power law tails for the time lapse distributions. We observe that the clogging transition can be achieved in different ways. In a two-dimensional flat bottomed vertical silo (Fig. 3A–D) we show that the system becomes unclogged (Φ > 0) as the head of grains above the orifice (h) is reduced, the intensity of vibration (Γ) is increased, or the outlet size (L) is enlarged. In a two-dimensional inclined and vibrated hopper, we also observe the transition to an unclogged regime when we tilt the silo, therefore reducing the effect of gravity (Fig. 3E–F). Note that reducing pressure as a strategy to ease arch destabilization by vibration was already anticipated by Valdes and Santamarina19. Finally, we use a 3D silo which is locally vibrated at the very orifice (Fig. 3G) to examine a Γ–L projection of the clogging phase diagram (Fig. 3H) in terms of Φ.
Time lapse distributions in three different silos.
(A) Photograph of the two-dimensional silo filled with 1 mm particles. (B) Time lapse complementary CDFs obtained using L = 4.50 and Γ = 0.26 for two different heights of the layer of grains (h > 6 cm and h < 6 cm). (C) Time lapse complementary CDFs obtained for h > 6 cm, L = 4.76 and several Γ as indicated in the legend. (D) Time lapse complementary CDFs obtained for h > 6 cm, Γ = 0.26 and several outlet sizes as indicated in the legend. (E) Sketch of the inclined hopper. (F) Time lapse complementary CDFs obtained using two different inclination angles. (G) Sketch of the 3-D hopper vibrated at the orifice7. (H) Phase diagram for the plane Γ–L obtained for the 3-D hopper. The values measured experimentally are marked by crosses (Φ = 0) or circles (Φ > 0). The colour scale from blue to green (as indicated by the colour bar) is a linear interpolation for the values of Φ. The dashed white line is a guide to the eye for the transition from Φ = 0 to Φ > 0.
Clogging is finally analysed on a model colloidal suspension, simulated using the Lattice Boltzmann method20,21, which is forced to pass through a constriction by means of an external pressure gradient that forces the solvent (Fig. 4A). Once again, we find that the time lapse distributions display power-law tails (Fig. 4B) while the burst size distributions remain exponential. The clogging transition can be achieved naturally by changing the temperature, which controls the interplay between colloidal particle fluctuations and the intensity of the driving force. Low temperatures lead to clogged states and high temperatures to unclogged states. Previous studies in colloids have focused on the mechanisms leading to the development of permanent clogs22; a scenario which is of practical relevance and corresponds to the regime where Φ = 0. Our approach is conceptually different as we infer, from the statistical analysis of the flow intermittencies, a situation in which Φ = 0 without the necessity of observing permanent clogs. We observe that the approach to complete obstruction in colloidal suspensions obeys the same universal scenario than in the human models and granular materials, evidencing that the transition to clogging is not very sensitive to the microscopic details of the system. The latter are relevant to identify the specific mechanism that controls the clog growth and the quantitative values of the parameters where clogging takes place (i.e. when Φ = 0).
Time lapse distributions of a colloidal suspension driven by a pressure gradient through a constriction.
(A) Illustration of a clog as obtained in the numerical simulation of the colloidal system passing through a bottleneck. (B) Complementary CDF of the time lapses obtained for an outlet size of radius 1.7 times the particle radius, a driving pressure ΔP = 5 10−5 (in lattice units) and two different temperatures (in units of the colloid characteristic kinetic energy, as indicated in the legend). The time is expressed in Stokes times, τst = R/〈Vy〉, the typical time it takes a particle of radius R to move a distance equal to its own size.
Discussion/conclusion
The foregoing analysis shows that clogging in a wide variety of systems can be understood as a transition between different intermittent regimes. We have identified an order parameter Φ that distinguishes between states with well-defined mean clog duration and states where this magnitude diverges. In the latter, the mean flow rate tends to zero (a situation still compatible with a finite mean burst size). The transition from clogged to unclogged states can be achieved in a variety of ways summarized in Table 1. All the strategies grouped in column A imply controlling the driving force (or pressure) at the orifice, by tilting a silo or reducing the layer of grains above the orifice, by placing an obstacle before the door for a sheep herd, or by reducing the pedestrians' desired velocity. Generally speaking, we can relate these with a compatible load CL, which is responsible for the development of clogging structures as proposed by Cates et al.23.
The variables in column B are related with the intensity of the background noise acting on the particles, for instance, the random force in the case of pedestrians, the external excitation in the case of silos or the temperature in a colloidal suspension. Following the proposal of Cates et al. we ascribe these variables to an incompatible load IL that can eventually destabilize the clogging structures. Finally, the outlet sizes grouped in column C should be related with the physical constrictions that govern the passage through the bottleneck: a characteristic length scale Λ, that manifests the local nature of clogging.
One might be tempted to consider the packing fraction φ of the sample at the orifice as the natural variable to define the state of the system. However, φ near the outlet is a variable that cannot be rigorously measured (since it is strongly dependent on the distance to the outlet) nor controlled (because it is spontaneously set by the system as a result of imposed driving force, gravity, layers of grains, etc.). Only a careful preparation of the initial φ before the very first burst might be controlled (see Ref. 41). Of course, it is expected that a system with extremely low packing fraction will never develop clogging, but in this case the value of CL at the bottleneck will also approach zero. Previous studies in colloidal suspensions have shown that clog formation is controlled by the local mechanisms that determine how an aggregate grows and sticks to a surface, again indicating that the average packing fraction is not relevant to capture the essence of clogging. Nonetheless, the intermittent flow regime that precedes clogging indicates that there exists strong correlation between particles in the neighbourhood of the opening. Such correlations are local and decoupled from the mean system concentration.
Identifying the generic nature of the clogging transition and the relevant parameters that control it allow us to sketch a qualitative state diagram (Fig. 5) which conceptually encompasses the many different situations presented in this letter. The diagram presents qualitative differences with the one proposed for the jamming transition24. The presence of a characteristic length scale highlights the finite-size nature of clogging, where the outlet size competes with the scale of the structures that allow particle motion near a blockade. This parameter accounts for collective processes25 which were identified near the jamming transition for athermal systems26 or close to the glassy transition for thermal ones27,28. It is likely that the nature of such mobile arrangements -developing on scales of several particle sizes- will be strongly affected by the specific boundary conditions at the outlet and their features will be related to the mechanical configurations controlling the arrest dynamics. For each specific situation (thermal/athermal, soft/hard, active/passive particles) the nature of the states landscape near the opening and its dynamical exploration can be extremely different. Nevertheless, the fact that we find strikingly similar signatures plea in favour of a unified scenario as proposed in Fig. 5. The quantitative assessment of the relevant parameters characterizing each of the diagram branches -that may depend on the specific situation- is left open for future investigation. Furthermore, the effect of the outlet geometry29, particle interaction30, or shear stresses31 on the proposed variables remains to be understood. At present, the insight gained in this work enables us -for instance- to explain the increased stability of clogs exhibited by suspensions when are subjected to higher fluid velocities32, or why ant traffic does not display clogging33,34. Ants are characterized by avoiding the exertion of pressure on each other, hence there is no compatible load at the bottleneck. This knowledge will also open new ways to tune and control flow in constrictions and can be used to minimize the harmful effects of clogging.
Proposed clogging phase diagram.
Clogging phase diagram where all the variables explored in different systems are grouped in three generic parameters: Λ (a length scale), which includes the relationship between the outlet size and particle size; IL (incompatible load), a load that leads to the collapse of the clogging structure, i.e. θ for pedestrians, Γ for silos and T for colloidal particles; CL (compatible load), typically related to the pressure or the driving force, i.e. vd for pedestrians, gravity and height of the layer of grains for silos, presence or not of the obstacle for sheep and fluid velocity for colloidal particles.
Methods
The methods were carried out in “accordance” with the approved guidelines. We explore the passage of particles through bottlenecks in four different scenarios: sheep passing through a gate, pedestrian simulations of room evacuation, the discharge of three different vibrated silos or hoppers and the flow of colloids through a constriction. In all cases the final goal is to obtain the complementary CDF of the time lapses (namely, 1-CDF) and use it as a tool to assess the state of the system. Experimental measurements provide the time at which the particles pass through the outlet. From these data, the time lapse τ between the passage of two consecutive particles is obtained. The histograms of τ display a power law tail τ −α. The exponents of these power laws are calculated by means of the method developed by Clauset, Shalizi and Newman10 which provides the exponent of the power-law tail and the minimum value τmin from which the fit is valid (note that the slope of the complementary CDF is α + 1). The power law breaks down at short times due to finite size effects. For instance, in the case of sheep, the typical dimensions of an animal, its velocity and the door width, all combine so that for short periods of time the power law breaks down. This time scale is then used to define bursts (e.g., groups of sheep separated by less than τmin) and clogs (time lapses longer than τmin). Additionally, the procedure gives an estimate of the fit accuracy, based on a number of realizations. In all cases, we find a p-value > 0.1.
Sheep passage through a door
The study presented here consists on recordings on the normal practices undertaken for the purposes of recognised animal husbandry. Hence, according to the Directive 2010/63/EU (European Union) on the protection of animals use for scientific purposes, no project evaluation by ethical committee was necessary. This directive explicitly states that it does not apply to the non-experimental agricultural practices or practices undertaken for the purposes of recognised animal husbandry or practices not likely to cause pain, suffering, distress or lasting harm equivalent to, or higher than, that caused by the introduction of a needle in accordance with good veterinary practice.
Data for the time passage of sheep have been collected at a farm in Cubel (Zaragoza, Spain). The herd comprises about 1500 sheep of Rasa Aragonesa breed and belong to a herd of selection inscribed in the genealogical book of the breed. From among them, a flock of young breeding mothers was picked, so the body mass and size of individuals in this subset is quite uniform. We observed this flock during 30 to 40 days and then the flock is replaced. The flocks comprise 75 ± 10 animals.
The sheep are kept in a barn and they are taken out every morning. Feeders inside the barn are stocked and a door is open. Then the sheep enter the barn in haste. This is the usual procedure carried out by the farmer and it is this entrance that we have been allowed to record every day during several months. The relevant dimensions are the width of the gate (77 cm) and the sheep width as measured at their hips (35 cm in average). In order to test whether an obstacle before the door is beneficial for the flow, a section of concrete drainpipe is set vertically in front of the door, as shown in Fig. 1A. This is a cylinder of 114 cm diameter and higher than the sheep (so the animals cannot see the door from behind) placed at a distance of 80 cm from the gate. For the flocks on which the obstacle was tested, the procedure was to record the entrance during a month, two weeks with an obstacle and two weeks without it, in order to verify that the flock behaved as the others when the obstacle was not there. After checking that there are no significant differences in the results of the different flocks, we aggregated all the data. The recordings of some days were useless due to poor conditions; in total, 3070 sheep were logged passing through the gate without an obstacle and 1432 with an obstacle in front of the gate.
To characterize the flow properties of the sheep, we have installed a standard surveillance video camera above the door (in a zenithal arrangement). A film is registered every day in a hard-disc and at the end of the month the data are collected. The recordings have a resolution of 704 × 576 pixels at 25 frames per second. A procedure akin to the photo finish used in track and field events is carried out to obtain an accurate timing for the passage of each animal. A line of pixels (see Fig. 1B) is sampled from every frame and stacked vertically, therefore forming an image where the vertical dimension is the time and the horizontal dimension the distance along the line of pixels –a spatio-temporal diagram, as shown in Fig. 1C. In order to increase the time resolution, we have sampled a five-pixel-thick line. Passage detection has to be made once the sheep have crossed the door, so this line is located at approximately one body length from the entrance, as depicted in Fig. 1B. We have nevertheless checked that our results are insensitive to the particular choice of this line. The head of every animal is marked manually in the spatio-temporal diagram and a simple image processing program produces a file with the passage time for every animal in the flock. With these files we produce the graphs of Fig. 1D and also obtain the time intervals τ between the passage of two consecutive sheep needed to build the cumulative histograms of Fig. 1E.
In order to define bursts and clogs, it is unavoidable to set a threshold for the minimum time lapse between two consecutive sheep above which the bursts are considered to be separated. A sound choice is the minimum value of τ (τmin) above which the power law holds, which is provided by the method used10. Another clue comes from the flow at maximum density: animals are then separated typically by time intervals that depend on the characteristic speeds and sizes of the system. Both clues point to a time lapse of about one second. We have tested that choosing values for τmin between 0.7 seconds and 2 seconds, made no significant difference in the results. The outcomes for a threshold of τmin = 1 s are displayed in Fig. 1F.
Pedestrian simulation
We have modelled the behaviour of a group of 30 pedestrians evacuating a room with periodic boundary conditions, meaning that pedestrians who leave the enclosure are reinserted in random positions inside the room once they are 3 m away beyond the door. In this way, the state of maximum density near the door is maintained. The simulations were performed using the Social Force Model put forward by Helbing and coworkers6 plus a fluctuating random force16,17 perpendicular to the door line (i.e. in the y-coordinate, see Fig. 2A). This fluctuating force is uniformly distributed in the range [−θ, θ], where θ is the noise amplitude.
The equations of motion were integrated using the velocity-Verlet algorithm with a time step Δt = 0.001 s. Fifty four simulations of 2.000.000 s each one (simulated time) were performed changing the initial configuration of the pedestrians and the parameters vd (desired speed), L (door width) and θ (noise amplitude), as shown in Fig. 2. The desired speeds were chosen with an average value as indicated and a dispersion of ± 0.05 m/s.
The fixed parameters of the model were: number of pedestrians, N = 30; room dimensions, 20 m × 20 m; for the Social Force Model: A = 11 N, B = 0.08 m; contact force parameter: kn = 180 kN/m, kt = 300 kN/m; relaxation time of the driving force: τp = 0.5 s; pedestrian radii r = 0.27 ± 0.03 m; pedestrian mass m = 80 ± 10 kg.
Silo experiments
The automated two-dimensional silo displayed in Fig. 3A has already been described in detail35. Brass spheres of 1 mm diameter confined in a monolayer start to flow until an arch is formed at the orifice and the outpouring is halted (this condition is detected with a video camera). At this point, a vertical 100 Hz sinusoidal vibration at constant acceleration Γ (measured in units of g, the acceleration of gravity) is switched on. We measure the time it takes to break the arch by inspecting the system with a video camera that can detect the moment at which the grains start to move with a resolution of 45 milliseconds. The silo is then turned upside down to collect the grains in the upper side and half turned again to start a new run. Typically, about two thousand arches are registered and broken for each case in order to get enough data to perform the statistical analysis shown. In different experimental runs we have explored the influence of the orifice size L and the vibration amplitude Γ. In general, we only considered the arches formed when the material head in the silo (h) is h > 6 cm (which is the silo width), but in some runs we have also measured the time taken to break the arches when the head is lower than this value. In the latter case, the pressure at the base of the silo is smaller.
The inclined two-dimensional hopper (Fig. 3E) consists in two Plexiglas sheets separated by a narrow frame allowing the confinement of 500 glass beads (4 mm in diameter) in a 5 mm wide gap. The rectangular silo is 6 cm wide and ends in a hopper with walls at 17 degrees with the horizontal that leaves an aperture of 12 mm (three particle diameters). The inner side of the bottom sheet, on which the beads roll, is covered with aluminium foil connected to ground to prevent electrostatic charging. A relay is used to open and close a gate at the opening. A speaker glued outside of the bottom Plexiglas sheet can make the system vibrate at the desired amplitude and frequency. A microphone below the aperture (inside the frame) detects the glass beads as they exit the hopper; this signal is used to analyse the discharge process. The entire system is fixed to an axis driven by a motor so that the beads can roll back and forth on the bottom sheet by changing the inclination angle. A set of photo-diodes sense the angle of inclination and the moment at which the hopper is emptied. An accelerometer attached to the bottom sheet measures the vibration acceleration amplitude.
A PC controls the motor and the gate. If the hopper is empty, the axis is turned so that the glass beads roll to the “upper” side of the silo. When driving the system back to the desired inclination, two deflectors direct the grains towards the hopper. Then, the speaker starts vibrating and the gate is opened. The microphone registers the discharge until the hopper is emptied and a new cycle begins. Typically, 200 discharges are carried out for the two inclination angles reported in this manuscript (20 and 60 degrees with respect to the horizontal). The vibration acceleration amplitude was 0.13 g and the fundamental frequency 150 Hz. Since at the end of the discharge the pressure at the orifice considerably depends on the filling level, we only consider in the analysis the first half of the discharge, where pressure is expected to vary marginally.
The microphone signal is processed to detect the peaks that correspond to the particle impacts. The signal is raised to the fourth power to reduce the signal to noise ratio and then a running average is performed to smooth out high frequency components. The maxima of the resulting signal are used as estimates for the instants when particles knock the microphone. Since many beads may knock the microphone within a short time interval, we most likely detect fewer maxima than beads have flown through the aperture. However, since we are interested in the statistics of long-lasting blockages, this loss of information at short time scales is irrelevant.
The eccentrically discharged hopper shown in Fig. 3F is described in a previous work9. It consists of a cylinder with a partially closed base (forming an angle of 45 degrees with the cylinder axis). The base is vibrated at a fixed frequency and amplitude by means of a piezoelectric element. A plastic sheet with a microphone attached to it is placed beneath the exit orifice. The sound produced by the impact of the falling grains is recorded and the time lapses between particles are measured. A minimum time lapse τmin = 0.1 s is used to sort between flowing and clogged states. We then calculate the average time lapse in the flowing state 〈tf〉 and the average time lapse in the clogged state 〈tc〉. For each orifice size (L) and acceleration of the imposed vibration (Γ), we compute the value of Φ = 〈tf〉/(〈tf〉 + 〈tc〉. To this end, the exponent (α) of the complementary CDF is obtained as explained above. If α ≤ 2, the value of the parameter Φ becomes zero (as 〈tc〉 diverges). In the cases where α > 2, 〈tf〉 and 〈tc〉 are directly calculated from the measurements in order to compute Φ.
Colloid simulation
We have modelled the motion of a colloidal suspension through a constriction using the lattice-Boltzmann method36 incorporating discrete solid spherical particles, of radius R. The colloidal particles interact with the surrounding fluid through the standard ‘bounce-back on the links’ method37. The same rule is applied to enforce stick boundary conditions at the solid walls that define the system geometry. Thermal fluctuations are incorporated using the scheme proposed in Refs. 38, 39, to ensure that in the absence of any forcing the suspension reaches thermal equilibrium.
In all simulations we consider a colloidal suspension confined between two parallel solid walls that have a circular orifice of modifiable radius. In the other two directions the system is periodic. The fluid parameters are chosen to ensure a Reynolds number, Re = UR/ν -based on the particle radius, R, the fluid kinematic viscosity, ν and the characteristic particle velocity, U- smaller than 1/10.
In all simulations presented here, the system sizes are 44 node wide in the transverse direction and 88 in the direction perpendicular to the solid walls. 128 colloidal particles of radius 5 lattice units are initially randomly distributed, corresponding to an average volume fraction φ = 0.4. The fluid is subject to a uniform force perpendicular to the walls, mimicking a pressure driven flow that pushes the colloidal particles through the opening. The forcing induces the accumulation of the colloidal particles in the neighbourhood of the orifice. To avoid overlapping, we include a short-range repulsion between colloidal particles40 and between the colloidal particles and the walls, except in the orifice region. Moreover, wall bounce-back is suppressed in the orifice region (allowing the fluid to flow through it) and the colloidal particles do not experience the short-range wall repulsion. The discrete representation of the colloidal particles on the lattice does not allow LB to recover exactly the diverging lubrication forces when solid surfaces approach to contact. We have included a short-range, pairwise approximation to the lubrication forces between all solid surfaces to prevent any overlap37.
Long time simulations are required to sample appropriate clogging events. To this end, in each simulation the colloidal particles are allowed to cross several times the system size. Eventually they accumulate at the orifice forming clogs. In each simulation we typically run 108 time steps and gather statistics over 105 colloidal particles passing through the orifice.
References
To, K., Lai, P. Y. & Pak, H. K. Jamming of granular flow in a two-dimensional hopper. Phys. Rev. Lett. 86, 71–74 (2001).
Haw, M. D. Jamming, Two-fluid behavior and “self-filtration” in concentrated particulate suspensions. Phys. Rev. Lett. 92, 185506 (2004).
Genovese, D. & Sprakel, J. Crystallization and intermittent dynamics in constricted microfluidic flows of dense suspensions. Soft Matter 7, 3889–3896 (2011).
Rees, D. G., Totsuji, H. & Kono, K. Commensurability-Dependent Transport of a Wigner Crystal in a Nanoconstriction. Phys. Rev. Lett. 108, 176801 (2012).
Helbing, D., Buzna, L., Johansson, A. & Werner, T. Self-Organized Pedestrian Crowd Dynamics: Experiments, Simulations and Design Solutions. Transportation Science 39, 1–24 (2005).
Helbing, D., Farkas, I. & Vicsek, T. Simulating dynamic features of escape panic. Nature 407, 487–490 (2000).
Moussaïd, M., Helbing, D. & Theraulaz, G. How simple rules determine pedestrian behavior and crowd disasters. Proc. Natl. Acad. Sci. USA 108, 6884 (2011).
Saloma, C., Perez, G. J., Tapang, G., Lim, M. & Saloma, C. P. Self-organized queuing and scale-free behavior in real escape panic. Proc. Natl. Acad. Sci. USA 100, 11947–11952 (2003).
Janda, A., Maza, D., Garcimartín, A., Kolb, E., Lanuza, J. & Clément, E. Unjamming a granular hopper by vibration. EPL 87, 24002 (2009).
Clauset, A., Shalizi, C. R. & Newman, M. E. Power-law distributions in empirical data. SIAM review 51, 661–703 (2009).
Helbing, D., Johansson, A., Mathiesen, J., Jensen, M. H. & Hansen, A. Analytical approach to continuous and intermittent bottleneck flows. Phys. Rev. Lett. 97, 168001 (2006).
Masuda, T., Nishinari, K. & Schadschneider, A. Critical Bottleneck Size for Jamless Particle Flows in Two Dimensions. Phys. Rev. Lett. 112, 138701 (2014).
Zuriguel, I., Pugnaloni, L. A., Garcimartin, A. & Maza, D. Jamming during the discharge of grains from a silo described as a percolating transition. Phys. Rev. E 68, 030301 (2003).
Lafond, P. G., Gilmer, M. W. Koh, C. A., Sloan, E. D., Wu, D. T. & Sum, A. K. Orifice jamming of fluid-driven granular flow. Phys. Rev. E 87, 042204 (2013).
Zuriguel, I., Janda, A., Garcimartín, A., Lozano, C., Arévalo, R. & Maza, D. Silo clogging reduction by the presence of an obstacle. Phys. Rev. Lett. 107, 278001 (2011).
Helbing, D. & Molnar, P. Social force model for pedestrian dynamics. Phys. Rev. E 51, 4282–4286 (1995).
Helbing, D., Farkas, I. J. & Vicsek, T. Freezing by heating in a driven mesoscopic system. Phys. Rev. Lett. 84, 1240–1243 (2000).
Sornette, D. Critical Phenomena in Natural Sciences. Springer-Verlag, Berlin (2000).
Valdes, J. R. & Santamarina, J. C. Clogging: bridge formation and vibration-based destabilization. Can. Geotech. J. 45, 177–184 (2008).
Desplat, J.-C., Pagonabarraga, I. & Bladon, P. LUDWIG: A parallel Lattice-Boltzmann code for complex fluids Computer Phys. Comm. 134, 273–290 (2001).
Düenweg, B. & Ladd, A. J. C. Lattice Boltzmann Simulations of Soft Matter Systems. Advanced Computer Simulation Approaches for Soft Matter Sciences III, Adv. Poly. Sci. 221, 89–166 (2009).
Wyss, H. M., Blair, D. L., Morris, J. F., Stone, H. A. & Weitz, D. A. Mechanism for clogging of microchannels. Phys. Rev. E 74, 061402 (2006).
Cates, M. E., Wittmer, J. P., Bouchaud, J. P. & Claudin, P. Jamming, force chains and fragile matter. Phys. Rev. Lett. 81, 1841–1844 (1998).
Liu, A. J. & Nagel, S. R. Jamming is not just cool anymore. Nature 396, 21–22 (1998).
Berthier, L., Biroli, G., Bouchaud, J.-P. h., Cipelletti, L. & van Saarloo, W. Dynamical Heterogeneities in Glasses, Colloids and Granular Media Oxford University Press (2001).
Lerner, E., During, G. & Wyart, M. A unified framework for non-Brownian suspension flows and soft amorphous solids. Proc. Natl. Acad. Sci. USA 109, 4798–4803 (2012).
Donati, C., Glotzer, S. C. & Poole, P. H. Growing Spatial Correlations of Particle Displacements in a Simulated Liquid on Cooling toward the Glass Transition. Phys. Rev. Lett. 82, 5064–5067 (1999).
Weeks, E. R., Crocker, J. C., Levitt, A. C., Schofield, A. & Weitz, D. A. Three-Dimensional Direct Imaging of Structural Relaxation Near the Colloidal Glass Transition. Science 287, 627–631 (2000).
Thomas, C. C. & Durian, D. J. Geometry dependence of the clogging transition in tilted hoppers. Phys. Rev. E 87, 052201 (2013).
Trappe, V., Prasad, V., Cipelletti, L., Segre, P. N. & Weitz, D. A. Jamming phase diagram for attractive particles. Nature 411, 772–775 (2001).
Bi, D., Zhang, J., Chakraborty, B. & Behringer, R. P. Jamming by shear. Nature 480, 355–358 (2011).
Muecke, T. W. Formation fines and factors controlling their movement in porous media. Journal of Petroleum Technology 31, 144–150 (1979).
John, A., Schadschneider, A., Chowdhury, D. & Nishinari, K. Trafficlike collective movement of ants on trails: absence of jammed phase. Phys. Rev. Lett. 102, 108001 (2009).
Boari, S., Josens, R. & Parisi, D. R. Efficient Egress of Escaping Ants Stressed with Temperature. PloS ONE 8 (11), e81082 (2013).
Lozano, C., Lumay, G., Zuriguel, I., Hidalgo, R. C. & Garcimartín, A. Breaking Arches with Vibrations: The Role of Defects. Phys. Rev. Lett. 109, 068001 (2012).
Cates, M. E., Stratford, K., Adhikari, R., Stansell, P., Desplat, J.-C., Pagonabarraga, I., & Wagner, A. J. Simulating colloid hydrodynamics with lattice Boltzmann methods. J. Phys.: Condens. Matter. 16, S3903 (2004).
Nguyen, N.-Q. & Ladd, A. J. C. Lubrication corrections for lattice-Boltzmann simulations of particle suspensions. Phys. Rev. E 66, 046708 (2002).
Adhikari, R., Stratford, K., Cates, M. E. & Wagner, A. J. Fluctuating lattice Boltzmann. Europhys. Lett. 71, 473 (2005).
Thampi, S. P., Pagonabarraga, I. & Adhikari, R. Lattice-Boltzmann-Langevin simulations of binary mixtures. Phys. Rev. E 84, 046709 (2011).
Stratford, K. & Pagonabarraga, I. Parallel simulation of particle suspensions with the lattice Boltzmann method Computers & Mathematics with Applications. 55, 1585–1593 (2008).
Uñac, R. O., Vidales, A. M. & Pugnaloni, L. A. The effect of the packing fraction on the jamming of granular flow through small apertures. J. Stat. Mech: Theo. Exper. P04008 (2012).
Acknowledgements
We thank E. Altshuler for fruitful discussions, L.F. Urrea for his technical support, J.J. Ramos, D. Lacasta and L. Figueras for his advising concerning sheep evacuation and T. Yagüe for allowing the recordings of sheep at his farm. I.Z., R.C.H., C.L., A.J., D.M. and A.G. acknowledge support by MINECO (Spain) Project FIS2011-26675. A.G., D.M. and R.C.H. acknowledge support from a University of Navarra PIUNA project. C.L. acknowledges support from Asociación de Amigos, Universidad de Navarra. D.R.P., L.A.P., P.A.G. and J.P.P. acknowledge support from ANPCyT (Argentina) grant PICT 2011-1238. E.C. is supported by ANR Jamvibe and CNES grants. I.P. acknowledges financial support from MINECO (Spain), Project FIS2011- 22603, DURSI Project 2009SGR-634 and Generalitat de Catalunya under program Icrea Academia.
Author information
Authors and Affiliations
Contributions
I.Z. conceived the idea and coordinated the different groups. I.Z., L.A.P., E.C., D.M., I.P. and A.G. participated on the main discussions. I.Z., I.P. and A.G. wrote the paper. I.Z., L.M.F. and A.G. performed the experiments of sheep. D.R.P. simulated the pedestrian room evacuation. I.Z., C.L. and A.G. carried out the experiments with the vertical vibrated silo. P.G., J.P.P. and L.A.P. performed the experiments with the inclined hopper. A.J., E.C., D.M. and A.G. carried out the experiments with the eccentrically discharged hopper. R.C.H. and I.P. simulated the colloids. A.J. and C.L. did the statistical analysis. C.L. drew the figures.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Video showig the sheep passing through a narrow gate.
Supplementary Information
Video showig the sheep passing through a narrow gate.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Zuriguel, I., Parisi, D., Hidalgo, R. et al. Clogging transition of many-particle systems flowing through bottlenecks. Sci Rep 4, 7324 (2014). https://doi.org/10.1038/srep07324
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07324
This article is cited by
-
CFD-DEM model of plugging in flow with cohesive particles
Scientific Reports (2023)
-
Flow rate resonance of actively deforming particles
Scientific Reports (2023)
-
Fish evacuate smoothly respecting a social bubble
Scientific Reports (2023)
-
On the dual effect of obstacles in preventing silo clogging in 2D
Communications Physics (2022)
-
Role of cohesion in the flow of active particles through bottlenecks
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.