Abstract
As we bring tubulin protein molecules one by one into the vicinity, they self-assemble and entire event we capture live via quantum tunneling. We observe how these molecules form a linear chain and then chains self-assemble into 2D sheet, an essential for microtubule, —fundamental nano-tube in a cellular life form. Even without using GTP, or any chemical reaction, but applying particular ac signal using specially designed antenna around atomic sharp tip we could carry out the self-assembly, however, if there is no electromagnetic pumping, no self-assembly is observed. In order to verify this atomic scale observation, we have built an artificial cell-like environment with nano-scale engineering and repeated spontaneous growth of tubulin protein to its complex with and without electromagnetic signal. We used 64 combinations of plant, animal and fungi tubulins and several doping molecules used as drug and repeatedly observed that the long reported common frequency region where protein folds mechanically and its structures vibrate electromagnetically. Under pumping, the growth process exhibits a unique organized behavior unprecedented otherwise. Thus, “common frequency point” is proposed as a tool to regulate protein complex related diseases in the future.
Similar content being viewed by others
Introduction
High frequency electromagnetic and mechanical oscillations of proteins in the literatures: A common megahertz frequency domain. High frequency electromagnetic oscillations and the effect of temperature in proteins is an exciting field of research1, because of their potential applications in the medical science. Distinct vibrational modes of proteins in the high frequency domain stems from intra-molecular degrees of freedom of proteins, every single drug molecule and biological essentials have a specific vibrational signature2. In proteins, depending on the vibrational mode triggered by an external electromagnetic frequency, the relaxation time could change from fifty nanoseconds (109 Hz ~ GHz) to a few hundred microseconds (106 Hz ~ MHz)3. However, physical protein folding, if it is very fast then takes a few microseconds and if slow then a few seconds (Hz)4. Therefore, electromagnetic oscillations are faster than microseconds, while, mechanical oscillations sustain for microseconds and higher. Obviously, for some proteins there is a time gap between electromagnetic and mechanical oscillations, for some proteins the survival for microseconds is the “common frequency point”. In this case, the common point is the inverse of microseconds that is the megahertz frequency. In summary, if in a particular protein, the electromagnetic and mechanical oscillations have a common time or frequency region where, both electromagnetic and mechanical oscillations merge, then we might manipulate one with another. Since mechanical oscillations are local, can we modulate the protein folding & its complex formation from isolated proteins using megahertz electromagnetic signals, non-locally? Here, we make a journey from atomic scale live imaging of protein complex formation to the verification of the observations made in the cell-like environment and explore the common megahertz frequency region for the tubulin protein, which is 0.8 to 8 microseconds5. It means for tubulin protein if we pump electromagnetic signal, around 2.25 MHz and 0.225 MHz, then the protein complex i.e. microtubule formation would unravel unprecedented features.
The rate of microtubule growth is surprisingly distinct across the species to regulate the vital cell processes; the regulation is disrupted, if there is a modest change in this rate6. Therefore, one can tune the delicate cellular features like the chromosomal instability7, the nuclear transport8 simply by regulating the spontaneous growth and decay of microtubule, i.e. dynamic instability. The tubulins from plant, animal and fungi retains 90–95% genetic similarity9, yet the plant-microtubules rapidly recognize to re-organize with the environmental changes, however, the animal or the fungus cannot, in contrast the animal-microtubules are extremely sensitive to regulate the growth precisely10. The universal growth-rate control mechanism cutting across the species is unresolved—several basic questions of this primary activity of the living cells have remained unanswered. For example, no in vitro synthesis could reproduce the lower (200 nm) and the upper length limits (24 μm), as observed in vivo wherein the limits follow a unique relationship with the cell-shape. How microtubule defines its limits? The unlimited growth and the random speeds of growth are always observed in vitro, even, the dynamic instability is modeled as a stochastic & a random process11. Yet, the major contemporary discoveries on dynamic instability cannot explain why in vitro growth has no limits, i.e. what that limits microtubule's growth12,13,14.
The recent discovery of electromagnetic interaction of tubulin and microtubule
Recently, quantum tunneling image of single tubulin protein molecule15 and microtubule were taken and it has been imaged live how protofilaments get isolated step by step when water channels are taken out of the microtubule core16. It is also established now that using nanoelectronics set up one could trigger electromagnetic frequency and tubulin protein, microtubule responds remarkably at particular kHz, MHz and GHz ac signal15,16. The literatures have argued for the concerted actions of tubulins with the stabilizers and de-stabilizers to regulate the microtubule dynamics14; however, no state-of-the-art study is done to underpin the origin and mechanism of such concerted action. Thus, the studies have also neglected the possibility that all isoforms & homologs of plant, animal and fungal tubulin, drug molecules and ions inside a single cell17 could still follow a single energy exchange protocol to decide collectively the speed and the growth limits. Here we advance recent discovery on tubulin and microtubule15,16 to explain the long known synchronous or concerted action of proteins14.
A description of current study
We carry out atomic scale manipulation of single Porcene brain neuron extracted single tubulin protein and observe self-assembly of protofilaments, which occurs naturally, using similar techniques as described before15,16. Then we trigger ac signal at 37 MHz, which speeds up the self-assembly, we do not use any GTP. Since synchronization of tubulin assembly in solution is a well-studied phenomenon18, we repeated the same experiment in an artificial cell-like environment that works as a cavity so that the pumped ac electromagnetic signal reflects within the geometrical boundary, repeatedly, to induce synchrony such that the spontaneous decay stops and the effect that is only visible to us is the effect of a pure growth. In the conventional non-synchronized in vitro synthesis, we do not observe a rapid mode or a silent mode, though the possibility for a “stop” mode19 and rapid-growth20 were suggested earlier. By introducing and disrupting synchrony, we could activate or deactivate the limiting length control and speed control in vitro in the solution and we provide live imaging how each molecule comes nearby and assemble.
We report remarkable observation that the pristine tubulins form the cylindrical shape without GTP molecule even in solution, just like that we observed in Scanning Tunneling Microscope (Why does microtubule grow and shrink21?), using particular resonance frequency of tubulin22 (Some resonance peaks for tubulins are: [37, 46, 91, 137, 176, 281, 430] MHz; [9, 19, 78, 160, 224] GHz; [28, 88, 127, 340] THz (see Movie 1 online for quantum tunneling images); Some microtubule resonance peaks15,16 are: [120, 240, 320] kHz; [12, 20, 22, 30, 101, 113, 185, 204] MHz; [3, 7, 13, 18] GHz, see Movie 2 online for quantum tunneling images) which is consistent with earlier findings23,24, that challenged the role of GTP25. By collecting tubulin samples from species that radically differs in genetic signature [porcine (brain neuron), human (MCF 7 active breast cancer cell), fungi26 (Agaricus bisporus mashroom) and plant (six days old soybean germ lings)] we have experimentally determined the particular frequency domain that activates the protein molecules for a particular species. Such a sharing of the frequency-space is unprecedented. However, the tubulins extracted from the breast cancer cells are so sensitive to synchrony that on application of any ac frequency from 1 kHz to 50 MHz they grow limit-less, thus, one could detect the presence of cancer tubulin directly using the synchrony-test27. The GTP molecule, like other neuro-drugs, controls the microtubule growth limits. The rule that we observe in our experiment is that the known positive catalyst molecule for synchrony18 acts as stabilizer and grows microtubule to a longer limiting length and at a faster speed, while, the negative catalyst does the reverse i.e. acts as a de-stabilizer molecule.
Experimental section
Different solutions of tubulins
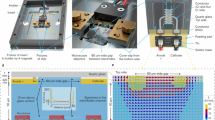
We prepare protein solutions as described in the microtubule growth protocols described in the Cytoskeleton Inc. company manuals (available online). The certain minor changes made in the advised protocol are noted here. Porcine (brain neuron), human (MCF 7 active breast cancer cell), fungi (Agaricus bisporus mushroom) and plant (six days old soybean germ lings), samples were obtained from Cytoskeleton Inc kept at −70°C. Ingredients are lyophilized tubulin, PIPES, General tubulin Buffer, GTP Stock, DMSO, PEG, Taxol, Glycerol, Colchicin etc. Porcine's brain extracted tubulins were received from Cytoskeleton (Denver, CO), preserved at −80°C. To polymerize tubulin into microtubules, Microtubule cushion buffer (60% v/v glycerol, 80 mM PIPES pH 6.8, 1 mM EGTA, 1 mM MgCl2) was added to the general tubulin buffer (80 mM PIPES pH 7, 1 mM EGTA, 2 mM MgCl2) and/or GTP solution. Solution Pr combinations were: Pure tubulin+H2O (pH ~ 7.0), Pure tubulin+H2O+MgCl2, Pure tubulin+H2O ± MgCl2 ± GTP stock. Solution Cl, we kept identical procedure for all four species, exactly as described in the cytoskeleton website for all species; except that for fungi GTP stock had 10% PEG. Stock solutions were rotated at 15000 rpm, 0°C, 30 minutes to de-polymerize prior use. For breast cancer cells, 10% Glycerol, for fungi 10% PEG, for Soybean 5% DMSO was used prior ac pumping. We prepare the protein solution, the drug molecules are added in nano-molar concentration whenever required. For scanning tunneling microscope imaging (Figure 1a,b) and Scanning Electron Micrograph (Figure 1c,d) solutions were dropped on the atomic flat HOPG substrate.
STM images of single tubulin self-assembly into protofilaments:
(a). Tubulin molecule (left most). Series of STM images (2 V tip bias 10 pA current) of three protein molecules, they form a perfect linear assembly and stabilize. Scale bar for first four images 3.8 nm, for the last two images (one above another), scale bar is 5 nm. Protofilaments connected (extreme right), scale bar 8 nm. (b). STM images at 2.1 V tip bias 30 pA current, left to right frequencies are noted in Hz, M means mega 106 Hz, G means Giga 109 Hz, scale bar for all images 4 nm. (c). SEM image of a typical artificial cell environment (scale bar top left 1 mm). A circular region is expanded in its right, one electrode associated region is highlighted below (scale bar 4 μm), small hair like structures are microtubule like cylinders, one cylinder like structure is zoomed in its left (scale bar 150 nm). (d). Experimental (red) and theoretical46,47,48,49,50 (blue, see supporting online text) average length of microtubules (standard deviation ~200 nm) as a function of a.c. signal frequency (top left). AFM images of microtubules (right, top-to-bottom) grown at 500 kHz (scale bar is 7 μm), 5 MHz (scale bar is 5 μm) and 15 MHz (scale bar is 7 μm) on SiO2/Si substrate.
Experiment in Cell-like environment: Multi-electrode clocking to detect synchronous signaling
The Figure S1A online shows chip is created by e-beam lithography and the electrodes are made of gold, the heights of the electrodes were ~500 nm, all geometrical parameters replicate a typical cell environment as described in the literature28. The artificial cell's circuit connection, measurement apparatus and instruments during measurement are shown in Figure S1 A online. The cell shape is square, the geometry of the local boundaries is selected as argued earlier mathematically11 so that the microtubules are mostly found in the homogeneous circular electric field region with a diameter of ~ 100 μm in the central part of the artificial cell-chip. A living cell has nano-gaps in the cell membrane to exchange the molecular & the ionic components; we have kept this provision in the artificial cell designed by us (see PC and MS 200 nm wide nano-gaps in Figure 1b and 2a). It should be noted that if the cell dimensions change, the limiting parameters growth rate and dimension described in this manuscript would change as electromagnetic field induced protein synchrony is activated by typical features of the cell geometry (height, width and length). We did a very interesting study, kept cell dimensions very large>500 μm and tried to see how we reach conventional control-less microtubule re-constitution process, we found that plant microtubule grows ~500 μm, animal and fungal grow ~80–100 μm.
Switching between synchrony and de-synchrony to switch between two kinds of in vitro processes (Also see Figure S1 online):
(a). The replica of a living cell, with PCMS ion gates and heat bath at 37°C, cell dimension of Figure 2A fixed for all species (200 μm), two 200 nm ion-channels. FG is function generator and connected circuit is the ac pumping circuit. L, E, T signals and two cables from PCMS is connected to an oscilloscope. Signals of synchrony are demonstrated on top, phase de-synchrony in the middle and amplitude de-synchrony is at the bottom. An AND gate inside SDC checks whether signals arrive at the same time, or same amplitude if “yes” we see “1” in the oscilloscope and if “no” then “0”. (b). Growth rate is switched off by disrupting synchrony in three ways, de-synchronizing both phase and amplitude, (top), de-synchronizing only phase (middle) and desynchronizing only amplitude (bottom) by sending noise into the solution. Pink arrow shows when noise is applied to de-synchronize. Blue arrow shows when noise is off and synchrony recovers slowly. Once microtubule nucleates from tubulin, a silent mode is not distinctly visible, hence recovery to synchronise is fast. The growth rate ratio measures the ratio of the growth rate of tubulin at a density higher than the natural synchrony to the growth rate at lower tubulin density.
We have used fixed cell-geometry-parameters for all the species and for all the drugs. We grew a micrometer thick film of tubulin solution on the chip, kept it inside a chamber at 37°C, the electrode-array remained dipped inside the water-film similar to a living cell. The electromagnetic signal is pumped through the cell boundary electrodes, ions in the buffer solutions are dragged into the ion channels namely PC and MS (200 nm gap between +ive and -ive electrodes), the event resembles the ion-membrane transport in a living cell. The ion-migration continues until the ions block the PC and MS gates. The chemical composition & the biological activities of a living cell dramatically differ than our artificial analogue; however, since we study the effect of synchrony, a clean artificial cell environment offer better results than a conventional in vitro experiment.
We varied the input pumping power 1 pico-watt (~50 mV, ~200 pA) to 1 femtowatt (~50 mV, ~200 pA), 3.7 MHz ac signal into the micrometer thick tubulin-water film created on a Si/SiO2 chip for 1 μs to 200 ms (T). Note that reducing ionic current is essential in solution using ion migration control protocol described above, if not, current would reach µA, then no signal is visible. The pump-time control enables us to capture the growth profile with a minute time gap. The chip embeds two independent electronics hardwares attached to it (Figure S1 online). First, PCMS electrodes pump an ac signal to the micrometer thick tubulin-water film created in the middle of the chip and second, an electronically independent L, E, T electrode system is connected to the synchrony-detection-circuit. The L, E and T electrodes do not cross talk, they collect signals from various parts of the tubulin-film, feed them to the SDC circuit and whenever SDC get signal at a time (between 0.1 ns) with the same phase and amplitude, it generates the logic output as "one" and if not it is "zero" (Figure 2a).
Direct and indirect measurement of growth rate
We take out the chip after pumping for a very short duration, dry and using Raman spectroscopy, we confirm that the nanowires are truly microtubule15,16. Using AFM we measure the length of the microtubules produced to get the maximum average length <L> and finally, we calculate <L>/T as the growth rate. The microtubule grows at around ~10 μs to the maximum length <L> ~24 μm. For the porcine, breast cancer, soybean & mushroom tubulins, the duration T is 10 μs, hence, the growth rate is 24 μm/10 μs~ 1.44 × 107 μm/min, at tubulin concentration 200 μM — orders faster than the expected rate of ~1–10 μm/min. Switching off the ac signal from outside disrupts even the natural growth of microtubule for several seconds, we dry the film for determining <L>. Though indirect, our growth parameters are as consistent as direct interferometer measurement. We cannot attach that set up with the existing complex cell-like architecture and associated electronics. Therefore, we claim tubulin's incredible rate of growth moderately, until interferrometric set up in cell like environment confirms the rate, which is not possible now technologically.
Results and discussions
Live visualization of GTP less tubulin protein assembly: Why this unique common point between electromagnetic and mechanical is a remarkable opportunity?
We have recently reported atomic resolution quantum tunneling current images of tubulin protein and its complex microtubule nanotube15,16. Tubulin protein's Terahertz and Gigahartz spectroscopy (electromagnetic pump probe experiments) has been documented extensively, we have noted entire em resonance band above in Introduction. The electromagnetic oscillation frequency in a post-pumping scenario depends on the internal structural symmetries. For example, for tubulin protein if we pump at around THz, one relaxation peak would be around 30–40 GHz and one around 0.8–8 MHz, not below that5. On the other hand mechanical oscillations for tubulins that causes its folding, which means various organized structural changes vary from seconds to microseconds, fortunately for tubulin it is around microseconds. If a molecule needs microseconds time to change its conformation, then megahertz mechanical oscillations would possibly, trigger the folding. Since mechanical megahertz signal (say ultrasound) damps in contact, we apply electromagnetic ac signal to set of molecules in a specially built STM machine. Normal STMs cannot work in electromagnetic signals.
We dropped a solution of protein on HOPG as described before15,16, brought tubulin molecules around 8 nm average distance, if no electromagnetic field is applied the molecules move randomly. After applying ac field 3.7 MHz using an antenna around the STM tip, we observe that tubulin molecules start diffusing on the HOPG surface and form protofilament like structure as shown in Figure 1a. The described atomic scale visuals are GTP-less self-assembly. We provide one example where tubulin dimers in a few steps self-assemble into a protofilament like structure in absence of any GTP molecules nearby.
Live demonstration of one to one correspondence between electromagnetic and mechanical oscillations
Triggering ac signal inside the STM and carry out induced self-assembly of tubulin unravels how conformational change takes place. We changed electromagnetic pumping frequency and checked how different frequencies change the local density of states in the tubulin protein structure. The change in local density at particular frequencies also accompanies local structural changes. From STM images, it is clear that there are fundamental structural changes, we could switch from one conformation to another by applying suitable frequency in the GHz range we can switch tubulin protein to another conformation as shown in Figure 1b. See online Movie 1 wherein we have shown STM images of single tubulin as a function of ac resonance frequency, mapping how structural evolution occurs. Similarly, we have shown Movie 2 online wherein single microtubule tunneling current images are produced when different resonance ac frequencies are pumped simultaneously. If one compares the frequencies in two movies (Movie 1 and Movie 2), one can point out that in the MHz frequency domain there are common regions. Thus, GHz switching does not trigger self-assembly but the MHz triggering might do and the same event is observed at the ac induced self-assembly inside the STM chamber. The frequency region selectivity for engaging particular kinds of conformational changes establish that pure mechanical changes could be controlled in an atomically precise manner remotely using electromagnetic ac fields remotely.
Tubulins acquire a cylindrical shape even without GTP
We demonstrate in Figure 1b that the resonant oscillations of tubulins are alone sufficient to generate the microtubular structure. This is verified again in an ultra-thin water film of tubulin, the set up SEM image is in Figure 1c, schematic and circuit is in Figure 2a, (online Figure S1). The AC signal induced synchrony (synchrony = in phase oscillations) form the microtubules even in the absence of GTP, Taxol and the buffer solutions, but it breaks apart beyond a certain length ~4 μm. Thus, the synchronization brings tubulins into a cylindrical shape even without hydrolysis mechanism shown in Figure 1c, the GTP molecule provides the stability to grow longer, the hydrolysis do not define the cylindrical shape. However, we could not grow microtubule at all, in the absence of Mg2+ ions, since it controls the polymerization, not the GTP molecule. It has always been a great mystery in the microtubule growth that one GTP molecule is hydrolyzed but not the other one, then, what that GTP does sitting idle in every single tubulin dimer? This is clear now; one GTP hydrolyzes to strengthen the bonding between the small tubular units of the microtubule and the other one plays a vital role in global synchronization, which helps microtubule to grow much longer than 4 μm (up to ~24 μm in animals, Figure 1c). Since without GTP, the rapid growth rate turns a few thousand times faster, not 2 million times, as we observe in the GTP-case, therefore, the GTP is essential for synchrony that directly controls the growth rate. GTP was used in all experiments below. The growth rate of the microtubule is primarily the folding-time of 2D tubulin sheet into a cylindrical shape.
Measuring growth profile via length variation of microtubule for different kinds of tubulins
Since earlier experiments have already detected a MHz ac signal emission from the living cells and assigned it's source to the microtubule inside29 and we establish with live imaging that such a MHz electromagnetic pumping changes the conformation of a protein molecule, we now try to establish the same in a cell-like device, which is closer to a living cellular environment (Figure 2a). We varied the ac pumping frequency in the protein film in the artificial chip described above and measured average length <L> as described above in the experimental section. One of the most interesting aspects of <L> as a function of frequency plot is that the peak at which the longest microtubules dominate the chip is a frequency around 3.77 MHz as shown in Figure 1d, we show here how the surface appears at three distinct frequencies, the length distribution has low SD (~1–2 µm). This is a Gaussian like distribution, already the spectroscopic studies on tubulin protein folding have shown that around 2–3 MHz a very particular kind of protein folding triggers microtubule growth and we observe this experimentally. We have carried out extensive theoretical simulation to explain the protein-protein interaction in this process (see four level signaling in the supporting online text) and in the Figure 1d, the theoretical fitting curve is plotted. This MHz frequency range is the junction point where mechanical and electromagnetic oscillations of proteins overlap. Using nano-probes we have studied the signal transmission among the tubulin dimers in the solution (Figure S3,a, b, c), we have observed in phase signal exchange through the medium among proteins (Figure S3, d), a comparison between pumping and non-pumping scenario shows that there are fundamental differences in the growth rate (Figure S3 e). We have varied density of tubulin proteins, the average length of the microtubule produced is independent of the density of the tubulin protein in the solution and also independent of the rms voltage or power we apply in the form of ac pumping (Figure S3 f).
Tubulin-microtubule conversion is one example; several protein complex regulates vital cellular life activities. By changing the cell geometry, we tuned the homogeneous electric field region; only the soybean tubulins adjusted its limiting lengths and the growth rate with the changing environments, however, plant, animal and fungi tubulins follow characteristic growth profile as shown in Figure 2a.
Controlled reversible switching between synchrony and de-synchrony during growth
Though protein synchrony is well known in earlier studies, we have introduce clocking set up for studying simultaneous emergence of same phase same amplitude signal in a thin film of protein film30. Since the L, E & T electrodes (see Figure 2a) captures the electromagnetic signal emissions from solution just at the onset of microtubule formation (10 pW) and the input power of the solution is same with that of the output burst—one possible explanation for energy mismatch could be that thermal noise (8–30 THz) is absorbed by tubulins as shown earlier to feed self-assembly. Then the ac pumping only triggers coupling among proteins within ~100 µm, in the solution. When we induce protein de-synchrony artificially by sending a de-phased/random amplitude signal via L, E and T, electrodes, then it decreases the growth speed. If we break the synchrony using inputs of different amplitude ac signals, the limiting lengths change. Thus, by changing the parameters we can mimic conventional in-vitro growth process in our artificial cell system. In the Figure 2b we have shown a sequence of synchrony-de-synchrony-synchrony processes to establish that the process of synchrony is generic and it has one to one correspondence with the growth rate of the microtubule. In the de-synchronized state, we triggered synchrony again and re-start the silent & the rapid modes (Figure 2b). By comparing three cases of synchrony-de-synchrony switching, we find that the phase synchrony is the key to maintain the coupling among tubulins during growth. If growth nucleus (small parts of microtubule) survives during de-synchrony, as shown in Figure 2b middle, then the rapid mode is triggered faster. However, if the phase synchrony is not there but the amplitude synchrony survives as in the Figure 2b bottom, the faster growth falls rapidly and it takes time to recover. If both kinds of synchronies disappear, then we do not observe the polymerization for a certain time. Even if the noise is removed and the ac signal to activate synchrony is triggered, synchronization takes time; the onset of synchrony if disrupted turns to a slow process. Therefore, Figure 2b suggests that very well-known protein synchrony is simply discretized by ac signal so that we observe the rapid modes and the silent modes.
Detection of “silent mode” and a “rapid mode” during microtubule growth under electromagnetic pumping
As soon as the ac pumping starts, initially, the L, E & T signal transmission try to reach coherence repeatedly as we see that the L, E & T outputs jump in the oscilloscope. Within 3–4 seconds, the in-phase coherent output is visible, but the output amplitude is 30% of the input (Figure 2 a,b). If the pumping is stopped during a "silent mode", we found microtubules of only ~200 nm in length for tubulins of all the four species we studied (Figure 3b). We tried to pump smaller and shorter pulses, changed the tubulin-density to grow shorter than 200 nm, but failed, thus, it is the lower length limit. The "silence" is therefore essential to nucleate the microtubule up to the lower limit, (200 mm) from which the "rapid mode" takes over as the L, E & T signals show the logic state “one” and the output signal amplitude is ~100% of the input (Figure 2a bottom, 2b). We have shown the instrument readings during a typical measurement in the Figure S1 B online. Even if we pump the solution for a long time, or increase the density, the limiting length does not change, which is again independent of tubulin density and constant across the four species we studied, we call it a "rapid mode" (Figure 3b). At a high tubulin & Mg2+ concentration (>60 μM), the microtubule grows ~102–103 times faster due to the spontaneous protein-synchrony18, here, an induced synchrony increases the speed even further by ~103 times. This is consistent with the recent single microtubule growth-rate-study, which has established that since tubulins bind laterally and longitudinally together to form microtubule, any protocol that ensures pre-assembly of tubulins into a 2D sheet prior to chemical reaction would speed up the growth rate dramatically23.
Comparison between conventional in vitro and synchronized in vitro processes:
(a). Dynamic instability for an animal, plant and fungi samples; shows growth, catastrophe and recovery, as observed in conventional in vitro process. (b). Length variation for 6.1 seconds of growth for Porcine brain neuron-extracted tubulins, when we pump an ac signal (yellow trace in oscilloscope-captured image), emission from solution is measured as an ac signal output (blue). Growth stopped by rapid drying the micrometer thick film after ac pumping at 2.001 seconds (data of 100 chips each with 10 cells and 20,000 events in 6.1 seconds). We pump with ~1 μs pulse and dry; then ~2 μs pulse and dry; this way up to 20 ms. Then measure length of every single microtubule on the entire chip to get <L>, so we see variation 1 μs to 20 ms, with constant drying time. AFM image of the chip, scale bar from left to right are, 30 nm (first four), 300 nm (next four), 5 μm (next two). For AFM, Average maximum microtubule length <L>, for ~100 samples, synthetic conditions optimized to standard deviation SD~±10 nm for Lmin ~ 200 nm and SD~±200 nm for Lmax ~24 μm. AFM images for the entire 6.1 seconds in conventional in vitro process. (c). AFM images of chip for the conventional in vitro process capture only tubulins, time-lapse kept identical, the scale bar is ~20 nm.
If the cell-like device and the ac pumping are removed, the unlimited growth and the random growth rate are observed again and the two unique rapid and silent modes disappear (Figure 3c). In the conventional version the microtubule growth is perceived continuous, now our measurements find “stop” between two rapid growths, together it is very slow but strictly quantized, such a possibility was noted earlier when the metastable states of microtubule growth was detected19. Even the possibility of an extremely rapid mode was argued earlier20. It has also been argued that the dynamic instability might consists of two distinct phases and a phase transition occurs frequently during the growth itself31.
Switching between synchronized in vitro and conventional in vitro protocol: Difference between plant, animal and fungi tubulin dynamics appears and disappears
The synchrony-induced growth is similar for all the four species and 14 drug molecules, all growth profiles look similar to the one demonstrated in Figure 3b. In the living species, the tubulin is doped with Taxol, GTP, GDP and other drugs especially for the animal and fungal; therefore, in the living cells we observe a compound effect. Some tubulins absorb the drug molecules inside its secondary structures, some molecules affect the microtubule growth from outside, in both cases the synchrony-rule remains intact. The combination of drug molecules has a dramatic effect on determining the limiting lengths and the eventual speed of growth and it most cases the speed decreases even by 3–4 orders of magnitude as we add more number of drug molecules. Here, we add drug molecules to modify the in vitro growth rate32 significantly and to match the observed in vivo activity of the microtubule dynamics33. In Figure 4a we have switched back and forth between "conventional in vitro" process where the growth rate is very slow and the "synchronized in vitro" where the growth rate is very high to find that the initial chaotic fluctuation prior to the synchrony activation makes the process slower. We get similar growth plots for all the species even when we do not add noise but simply add drug molecules. Since, we get a cylindrical form with synchrony and without GTP or any molecular drug, we propose a model below Figure 4a, where we suggest as argued before23, that if a cylindrical shape is constructed before the reaction begins, the polymerization speed would be remarkably faster since the hydrolysis-induced bonding takes place at multiple tubulin-dimer junctions simultaneously.
Tubulins share electromagnetic frequency band in a complementary manner:
(A). We have plotted growth factor (how many times the 1 μm/min) during synchronized in vitro for three species. Sudden fall is the point where several drugs were added, growth returns the specific features observed in conventional in vitro process. Then, the more tubulin is added to supersede the drug effect and remove noise, as soon as synchrony is established, high growth returns, the difference between three species disappears. Below the plot, we schematically present our model, during silent mode, due to synchrony the cylindrical form is produced, then it absorbs energy and afterwards rapid assembly starts which releases energy, this is the rapid mode. (B). We plot ratio of the maximum average length <L> to the maximum length <Lmax>measured from the AFM chip as a function of frequency for all drugs and for all species put together. For three samples, MCF7 breast cancer cells, Fungi and Soyabean tubulins, we show AFM images when the chips were pumped with 500 kHz, 3.7 MHz and 20 MHz ac signals respectively. The scale bar is 10 μm.
The common minimum tubulin doping protocol valid across the four species
We have studied how frequency variation affects the coupling among tubulins and determined the maximum length of the microtubules obtained from the chip as described before for 64 cases (4 species and 16 drugs makes 64 test samples). The normalized frequency vs. maximum length plot in Figure 4b shows that in the lower frequency domain (~100 kHz) the plant tubulins (Soyabean tubulin and its mixture with drugs) synchronize, as a result they fail to absorb the drug molecules as efficiently as the animals or fungus—drug molecules require a higher frequency for inducing co-synchrony. This is consistent with the argument that animal and fungi share a similar protistan origin34,35. The plant microtubules tend to form unique patterns in the artificial cell under synchrony, as seen here in the AFM images —tuned by ac noise. Around ~1 MHz, the animal tubulins (Porcene neuron) synchronize but the fungal tubulins synchronize at a much higher frequency domain (~20 MHz). Thus, the plant animal and fungal tubulins synchronize at specific frequency domains. In plant, animal and fungal tubulins, the basic synchrony protocol is conserved, the addition of specialization via drug molecules is consistent. Why synchrony-activation-frequency regions are separated would remain an open question. However, the active breast cancer cell extracted tubulins reach synchrony at any frequency between 1 kHz–50 MHz, we see a straight line in the Figure 4b for cancer, which means the AFM images of the microtubules produced for any triggering ac frequency were identical statistically and no significant changes were observed. Thus, the synchrony-activation rule that is valid uniquely for plant animal and fungal tubulin is not valid for the cancer tubulin. Hence a simple synchrony test could reveal if a tubulin has structurally mutated to activate cancer in a cell27.
A database of growth rate and limiting length controls for all four species
Any parameter, positively or negatively interfering with the synchrony increase or decrease the limiting lengths and the growth speed respectively. In vivo, the soybean tubulin grows faster than the porcine or human tubulins16,36, which are even faster than the mushroom tubulins. However, all the limiting speeds and the lengths appear identical under ac pumping in Figure 4a—thus, tubulin acts as the basic synchronizer. The administered drugs to the tubulin solution prior pumping modulates the synchronization and changes the growth rate and the limiting lengths (Figure 5). For example, the Colchicin stops the rapid growth unlike a non-synchrony case37—taking us closer to in vivo microtubule growth; the Taxol keeps it unchanged. Changing the density does not alter the limiting lengths, this is a significant conceptual shift observed here from the previous studies38,39,40,41,42,43,44,45. When synchrony is active, instead of density, the coupling factor dominates as the control parameter, phase transition from one conformation to another is difficult to fit in rate equation42. Thus, a change in the tubulin density in the cells cannot affect dynamic instability. Theoretically, if the tubulin proteins act as a fundamental oscillator unit, the microtubule would act as an elastic tuning fork generating MHz oscillations44,45, as we observe here; such a MHz emission is already detected outside a living cell38 and we have experimentally demonstrated MHz oscillation in a single microtubule15,16. By applying the oscillator's synchronous communication models, one could theoretically generate the limiting lengths exactly as observed experimentally, following protocols described elsewhere46,47,48,49,50. Thus, the drug molecules determine the domain in which the synchronous MHz communication of tubulin protein-oscillators is active (40000 tubulins for 24 μm), the upper limit of this domain sets the maximum length and the minimum oscillators required to activate a synchrony-network of tubulins determine the minimum length.
Two tables showing universal limiting lengths and growth rate control in the entire living kingdom (we study 4 species, 16 drugs; thus, 64 samples):
The Limiting length (above) and growth rate (below) tables for synchronized in vitro starts with a case where GTP + Taxol + Mg2+ is added with tubulin as common apart from drugs. Notably, GTP and Epothilone A (Sorangium Cellulosum) have the same effect on limiting length and speed. Taxol decreases the difference between upper and lower limits, Vinblastin (Catharanthus roseus) CN2 & LOC does not help in the polymerization of microtubule in animal cells and in contrast to its presence in plant cell speeds up dynamic instability. For several drugs, the effect is independent of the species.
All drug-tubulin composition data produced in Figure 5 are in the presence of GTP, therein, it is evident that the fastest growth of the plant tubulins has matched the limiting growth parameters of the animal and fungi; this is in sharp contrast to the conventional belief39,40. Chaos & self-order impact tubulins structural transformation40. The observation suggests that when all the positive catalyst to synchrony acts as a stabilizer and the negative catalyst to synchrony acts as a de-stabilizer, then, the molecular mechanisms of local GTP hydrolysis are locally driven, still relevant.
Conclusion
The common MHz frequency region, wherein electromagnetic and mechanical oscillations of tubulins occur together was used to regulate the protein complex, microtubule formation both inside an STM and inside an artificial-cell. The length variation study remarkably supports “common frequency point”. The maximum length of microtubule grows as 3.77 MHz while theoretical study done previously suggest a common frequency point at around 2.25 MHz. This protocol could be used for several other proteins and their complexes. The apparent slow growth rate of microtubule self-assembly in normal condition could be made of a sudden rapid growth followed by a long pause and then a rapid growth once again. It is an extraordinary observation that there are quantized jump in the growth process. Two particular observations (i) rolling of 2D tubulin sheet into a cylindrical shape without GTP both inside STM and in solution and (ii) remarkable growth of cancer cell extracted tubulins, firmly establish that the protein synchrony regulates extreme conditions.
Recently it is argued that non-equilibrium phase transitions cause microtubule growth and decay in vivo43. It would remain an open question, how 40000 tubulins assemble in less than a microsecond (see supporting online materials). One possible answer that we have tried to provide here using STM and artificial cell study that electromagnetic energy exchange speeds up mechanical folding44. Thus, synchrony of tubulins and microtubules is well known45, limiting lengths could be fitted using the oscillator models46,47,48,49,50. However, there are 30000 and above proteins working relentlessly in our body, the “common frequency point” if it exists for all proteins, would open up a possibility to remotely cure diseases. The reason is that the majority of diseases affect the protein complex pathways and until now, it was believed that protein undergoes pure mechanical vibrations at low frequencies and electromagnetic at very high frequencies, this strategy of pinning the common point would open up the path for wireless treatment, which is not possibly mechanically.
References
Doster, W., Diehl, M., Leyser, H., Petry, W. & Schober, H. [Terahertz spectroscopy of proteins: Viscoelastic damping of boson peak oscillations.]. Spectroscopy of Biological Molecules: New Directions [Greve, J., Puppels, G. J., Otto, C. (Eds.)] [655–658] (Springer publications, Netherlands, 1999).
Upadhya, P. C. et al. Characterization of Crystalline Phase Transformations in Theophylline by Time-Domain Terahertz Spectroscopy. Spect. Lett. 39, 215–224 (2006).
Gilmanshin, R., Williams, S., Callender, R. H., Woodruff, W. H. & Dyer, R. B. Fast events in protein folding: Relaxation dynamics of secondary and tertiary structure in native apomyoglobin. Proc. Natl. Acad. Sci. USA 94, 3709–3713 (1997).
Aronsson, G., Brorsson, A. C., Sahlman, L. & Jonsson, B. H. Remarkably slow folding of a small protein. FEBS Lett. 411, 359–364 (1997).
Mithieux, G., Chauvin, F., Roux, B. & Rousset, B. Association states of tubulin in the presence and absence of microtubule-associated proteins. Analysis by electric birefringence. Biophys. Chem. 22, 307–316 (1985).
Desai, A. & Mitchison, T. J. Microtubule polymerization dynamics. Annu. Rev. Cell Dev. Biol. 13, 83–117 (1997).
van der Vaart, B., Akhmanova, A. & Straube, A. Regulation of microtubule dynamic instability. Biochem. Soc. Trans. 37, 1007–1013 (2009).
Bakhoum, S. F., Thompson, S. L., Manning, A. & Compton, D. A. Suppressing chromosomal instability in cancer cells by targeting microtubule dynamics. J. Invest. Med. 57, 533–534 (2009).
Tuszynsky, J. A. et al. The evolution of the structure of tubulin and its potential consequences for the role and function of microtubules in cells and embryos. Int. J. Dev. Biol. 50, 341–358 (2006).
Unger, E., Bohm, K. J. & Vater, W. Structural diversity and dynamics of microtubules and polymerphic tubulin assemblies Electron Microscopy Rev. 3, 355–395 (1990).
Margolin, G., Gregoretti, I. V., Goodson, H. V. & Alber, M. S. Analysis of a mesoscopic stochastic model of microtubule dynamic instability. Phys. Rev. E 74, 041920 (2006).
Masuda, H. & Cande, W. Z. The role of tubulin polymerization during spindle elongation invitro. Cell 49, 193–202 (1987).
Panda, D., Rathinasamy, K., Santra, M. K. & Wilson, L. Kinetic suppression of microtubule dynamic instability by griseofulvin: Implications for its possible use in the treatment of cancer. Proc. Natl. Acad. Sci. USA 102, 9878–9883 (2005).
Vasquez, R. J., Howell, B., Yvon, A. M. C., Wadsworth, P. & Cassimeris, L. Nanomolar concentrations of nocodazole alter microtubule dynamic instability in vivo and in vitro. Mol. Biol. Cell 8, 973–985 (1997).
Sahu, S., Ghosh, S., Hirata, K., Fujita, D. & Bandyopadhyay, A. Multi-level memory-switching properties of a single brain microtubule. Appl. Phys. Lett. 102, 12370 (2013).
Sahu, S., Ghosh, S., Hirata, K., Fujita, D. & Bandyopadhyay, A. Atomic water channel controlling remarkable properties of a single brain microtubule: Correlating single protein to its supramolecular assembly, Biosensors and. Bioelect. 47, 141–148 (2013).
Bardini, M. D. et al. Tubulin-based polymorphism (TBP): a new tool, based on functionally relevant sequences, to assess genetic diversity in plant species. Genome 47, 281–291 (2004).
Carlier, M. F., Melki, R., Pantaloni, D., Hill, T. L. & Chen, Y. Synchronous oscillations in microtubule polymerization. Proc. Natl. Acad. Sci. USA 84, 5257–5261 (1987).
Tran, P. T., Walker, R. A. & Salmon, E. D. A metastable intermediate state of microtubule dynamic instability that differs significantly between plus and minus ends. J. Cell Biol. 138,105–117 (1997).
Howell, B. & Cassimeris. L. Rapid regulation of microtubule dynamic instability in living cells. Mol. Biol. Cell 6, 1504–1504 (1995).
Bayley, P. Why microtubules grow and shrink. Nature 363, 309–309 (1993).
Ghosh, S. et al. Design and Construction of a Brain-Like Computer: A New Class of Frequency-Fractal Computing Using Wireless Communication in a Supramolecular Organic, Inorganic System. Information 5, 28–100 (2014).
Gardner, M. K. et al. Rapid Microtubule Self-Assembly Kinetics. Cell 146, 582–592 (2011).
Kueh, H. Y. & Mitchison, T. J. Structural Plasticity in Actin and Tubulin Polymer Dynamics. Science 325, 960–963 (2009).
Caplow, M. & Shanks, J. Evidence that a single monolayer tubulin-GTP cap is both necessary and sufficient to stabilize microtubules. Mol. Biol. Cell 7, 663–675 (1996).
Woolston, B. M. et al. Long-Distance Translocation of Protein during Morphogenesis of the Fruiting Body in the Filamentous Fungus, Agaricus bisporus. PLoS One 6, 0028412 (2011).
Jordan, M. A. & Wilson, L. Microtubules as a target for anticancer drugs. Nat. Rev. Cancer 4, 253–265 (2004).
Janulevicius, A., van Pelt, J. & van Ooyen, A. Compartment volume influences microtubule dynamic instability: A model study. Biophys. J. 90, 788–798 (2006).
Jelinek, F. et al. Microelectronic sensors for measurement of electromagnetic fields of living cells and experimental results. Bioelectrochem. Bioenerg. 48, 261–266 (1999).
Kiss, I. Z., Zhai, Y. & Hudson, J. L. Collective dynamics of chaotic chemical oscillators and the law of large numbers. Phys. Rev. Lett. 88, 238301 (2002).
Vandecandelaere, A., Martin, S. R. & Bayley, P. M. Regulation of microtubule dynamic instability by tubulin - GDP. Biochemistry 34, 1332–1343 (1995).
Walker, R. A. et al. Dynamic instability of individual microtubules analyzed by video light-microscopy-rate constants and transition frequencies. J. Cell Biol. 107, 1437–1448 (1988).
Fojo, T. & Menefee, M. Mechanisms of multidrug resistance: the potential role of microtubule-stabilizing agents. Ann. Oncol. 18, 3–8 (2007).
Baldauf, S. L. & Palmer, J. D. Animals and fungi are each others closest relatives - congruent evidence from multiple proteins. Proc. Natl. Acad. Sci. USA 90, 11558–11562 (1993).
Steenkamp, E. T., Wright, J. & Baldauf, S. L. The protistan origins of animals and fungi. Mol. Biol. Evol. 23, 93–106 (2006).
Vassileva, V. N., Fujii, Y. & Ridge, R. W. Microtubule dynamics in plants. Plant Biotechno. 22, 8. 171–178 (2005).
Vandecandelaere, A., Martin, S. R., Schilstra, M. J. & Bayley, P. M. Effects of the tubulin-Colchicine complex on microtubule dynamic instability. Biochemistry 33, 2792–2801 (1994).
Jelinek, F. & Pokorny, J. Microtubules in biological cells as circular waveguides and resonators. Electro Magnetobiol. 20, 75–80 (2001).
Goddard, R. H., Wick, S. M., Silflow & Snustad, D. P. Microtubule components of the plant-cell cytoskeleton. Plant Physiol. 104, 1–6 (1994).
Wasteneys, G. O. Microtubule organization in the green kingdom: chaos or self-order? J. Cell Sci. 115, 1345–1354 (2002).
Ogawa, T., Nitta, R., Okada, Y. & Hirokawa, N. A common mechanism for microtubule destabilizers-M type kinesins stabilize curling of the protofilament using the class-specific neck and loops. Cell 116, 591–602 (2004).
House, J. E. [Principles of Chemical Kinetics]. In Principles of Chemical Kinetics. [House, J. E. (Ed.)] [336] (Academic Press, Netherlands, 2007).
Katrukha, E. A. & Guria, G. T. Dynamic instabilities in microtubule cytoskeleton. Phase diagram. Biofizika 51, 885–893 (2006).
Marx, A. & Mandelkow, E. A model of microtubule oscillations. Eur. Biophys. J. Biophys. Lett. 22, 405–421 (1994).
Sanchez, T., Welch, D., Nicastro, D. & Dogic, Z. Cilia-Like Beating of Active Microtubule Bundles. Science 333, 456–459 (2011).
Lichtenberg, A. J., Mirnov, V. V. & Day. C. Dynamics of oscillator chains from high frequency initial conditions: Comparison of phi(4) and FPU-beta models. Chaos 15, 15109 (2005).
Pecora, L. M. & Carroll, T. L. Master stability functions for synchronized coupled systems. Phys. Rev. Lett. 80, 2109–2112 (1998).
Rössler, O. E. An Equation for Continuous Chaos. Phy. Lett. 57A, 2. 397–398 (1976).
Senthilkumar, D. V., Muruganandam, P., Lakshmanan, M. & Kurths, J. Scaling and synchronization in a ring of diffusively coupled nonlinear oscillators. Phys. Rev. E 81, 066219 (2010).
Lorenz, E. N. Deterministic nonperiodic flow. J. Atmos. Sci. 20, 130–141 (1963).
Acknowledgements
Authors acknowledge Eiichiro Watanabe and Daiju Tsuya of Nanotechnology Innovation Station, NIMS Sengen-site Nano-foundry sponsored by Ministry of Science, Education, Culture and Sports (MEXT), Govt. of Japan. The current research work is funded by Asian office of Aerospace R&D, Govt. of USA FA2386-11-1-0001AOARD104173 and FA2386 -10-1-4059 AOARD-10-4059.
Author information
Authors and Affiliations
Contributions
A.B. designed the work, S.S. and S.G. did the lab work, analysed data wrote paper and DF reviewed the work.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary text
Supplementary Information
Movie 2 microtubule resonance
Supplementary Information
Movie 1 Tubulin resonance
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Sahu, S., Ghosh, S., Fujita, D. et al. Live visualizations of single isolated tubulin protein self-assembly via tunneling current: effect of electromagnetic pumping during spontaneous growth of microtubule. Sci Rep 4, 7303 (2014). https://doi.org/10.1038/srep07303
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07303
This article is cited by
-
Probing the existence of non-thermal Terahertz radiation induced changes of the protein solution structure
Scientific Reports (2021)
-
Consciousness and Quantum State Reduction—Which Comes First?
Activitas Nervosa Superior (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.