Introduction

X-ray and neutron imaging1 as well as small angle scattering (SAS)2 are invaluable tools for structural characterization in material sciences and applied studies. Their applications span a range from fundamental hard matter sciences via engineering and soft matter materials research to applications in medical diagnostics. While imaging provides direct real space access to individual structures typically in the micrometer range and above, small angle scattering enables statistical structural characterizations in the sub-micrometer range. Due to its statistical nature the application of SAS is limited to samples that are homogeneous within the probed region. The investigation of complex heterogeneous samples apart from model systems therefore requires spatially resolved approaches as provided by imaging. Imaging, however, is in general limited to the study of larger structures and it is hence the intermediate range of largely hierarchical structures, which poses a major challenge in nowadays material science and corresponding method development. The efficiency of conventional SAS instruments in this regime is poor, as the required angular resolution implies high collimation and coherence demands at significant cost of intensity3. Spatial resolved studies are therefore very limited, although significant efforts have been made on such instrumentation.

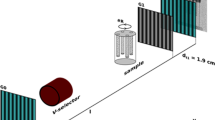
The introduction of grating interferometers for dark-field contrast imaging (Fig. 1) provided a 2 order of magnitude efficiency gain4 for approaching structures in a SAS regime, where direct space imaging methods begin overlapping the resolution range of scattering methods. Only grating interferometry4,5 paved the way for the broad application of dark-field (DF) scatter contrast imaging1,6,7 exploiting angular information in this regime. DF scatter images held the promise to reveal SAS information in imaging6 even with 3-dimensional resolution7.

Figure 1
figure 1

Schematic sketch of Talbot Lau grating interferometer set-up including three gratings and the corresponding distances and sample area referred to in this work; the cosine modulation function at the analyzer grating right in front of the detector is sketched as well.

Full size image

Over the past decade dark-field imaging with X-rays6 as well as with neutrons7 has turned out as a remarkable success8,9,10,11,12,13,14,15,16,17,18,19. Applications of dark-field contrast with neutrons up to now concentrate mainly on engineering materials15 but especially also magnetic materials16,17,18,19, where neutrons provide remarkable contrast due to their magnetic moment. For X-ray dark-field contrast imaging the ability of this technique to access soft tissue early on moved the focus to medical applications in particular with regard to cancer diagnostics and research9,10,11.

However, corresponding results up to now are qualitative, providing mainly image contrast between more or less scattering into a vaguely defined angular range. While the successful application as such underlines the wide spread need of corresponding structural information8,9,10,11,12,13,14,15,16,17,18,19, DF contrast imaging has yet to be explored fully in order to create the experimental approaches and analyses tools to fulfill its promises to serve as a scientific technique providing quantitative structural information in the SAS range. The success of the yet qualitative method triggered a remarkable effort in fully understanding and describing the measured signals theoretically in order to finally extract quantitative information13,20,21,22,23,24,25,26,27,28,29.

The solution introduced in this paper overcomes such limitations and can serve (i) to utilize the 2 order of magnitude gain4 of grating based dark-field contrast for conventional SAS studies in the ultra-SAS (USAS) regime2 and (ii) to finally provide access to such structural information beyond direct spatial resolution in imaging experiments6. Consequently (iii) it also enables informed and correct interpretations of up to now achieved qualitative DF scatter images. Hence the approach (iv) introduces the potential for quantitative structural SAS investigations with 3-dimensional tomographic resolution with (v) an efficiency allowing broad application through the use of lab x-ray sources as well as neutron sources. The possibility of measuring SAS functions for several voxels of a volume without the need of any rastering protocol, like nowadays required in a corresponding SAS experiment with a pencil-beam30, will open new ways and extend the potential of non-destructive characterization of materials.

In imaging with a Talbot-Lau grating interferometer a cosine modulation function is measured in every pixel of an image by scanning one of the gratings to achieve sub-pixel resolution of the interference pattern induced by a phase grating (Fig. 1). Thus not only the conventional attenuation image, which corresponds to the mean intensity of this pattern in a pixel, but also a differential phase contrast image and a dark-field image can be generated from the data. The phase contrast is measured by the relative phase shift of the modulation pattern and allows for mapping the refractive index distribution providing complementary image contrast in many cases in addition to the attenuation contrast image. Phase imaging4,5 is a well-established quantitative tool e.g. enabling x-ray imaging of low contrast materials like biological tissue samples, polymers or fibre composites. The dark-field signal is based on the relative visibility, i.e. modulation amplitude and is related to small angle scattering induced by the sample by sub-image-resolution structure sizes. The dark-field signal hence provides access to structural information beyond direct spatial resolution of the imaging instrument.

However, up to date most efforts to achieve quantitative information have either been limited to establishing relations between the signal measured and the thickness7,12,13,20,22,23,26,29, which in turn allows utilizing conventional tomographic reconstruction, i.e. retrieving the corresponding signal in 3D, or to solutions for very specific scattering structures with the potential to describe the signal when the sample parameters are known in detail beforehand27,28. The former attempts in general re-establish the approximation already published a decade ago31,32 and used for first tomographic reconstructions of the dark-field signal from a grating interferometer7. There the signal is described as a convolution of a Gaussian scattering function with the width

and the cosine response function of the grating interferometer7,26,29. Here σ, N and R are denoting the position dependent scattering cross section, particle density and correlation length of scattering structures in the sample, respectively. The integration is over the path of the radiation denoted with t. Note that the parameter fB corresponds to what was later called “linear diffusion coefficient” and assigned “ε” and “Ω” for x-rays26 and neutrons29, respectively, without further specifying dependencies, while B was later denoted “σ” for both. However, such simple Gaussian approximation is not suited to extract quantitative small-angle-scattering (SAS) information2 conveying a number of parameters like the scattering power, involving thickness, concentration and scattering cross section, as well as structural correlations; this implies that corresponding quantitative information is not accessible from a single measured parameter like the modulation amplitude. Hence, all descriptions also in the latter attempts named above27,28 are currently only suited to describe a priori well-known systems and systematic behavior related to thickness and eventually concentration etc.

However, for the case of plane wave illumination (without source grating) and a sample placed upstream of the phase grating W. Yashiro et al.21 achieve a more general result and thorough description of the measured signal via rigorous wave calculations. This way the authors manage to relate the modulation contrast measured at different Talbot orders21,24 to structural information. Correspondingly the authors find a limited means to probe such dependence via a scan of the distance L2 (Fig. 1) for the geometry of the plane wave case they are referring to. In this works it is already pointed out and shown experimentally that in such manner probed functions relate via Fourier transformation to small angle scattering functions. However, some important implications for thorough measurements and interpretations stay unrevealed this way, as we will discuss in the light of our more general approach.

A completely different recent approach attempts to extract the scattering function by de-convolving the measured signal with the instrument function and thereby deriving the scattering function25. However, such an approach is also limited concerning achieving a meaningful SAS function ready for quantitative analyses of structural parameters as evident when dealing with a cosine resolution function. Correspondingly, in Ref. 25 no claim is made to establish any quantitative relationship to structural sample parameters.

In contrast to earlier attempts the problem is to be solved in a more general approach here, without employing detailed wave calculations and specifics of the grating interferometer. This will allow to arrive at a high level general solution for the SAS information contained in modulated beam measurements of which grating interferometry is the most prominent and promising example. We will simply employ general and well known high level SAS theory and boundary conditions to provide not only a clear relationship between the data measured and quantitative structural SAS information that can hence be extracted, but also the means of the measurement strategy suited to do so and to achieve such fully SAS-equivalent information.

Results

As the principles of measurements with neutrons and x-rays are equivalent related to this technique, no distinction shall be made between those here.

Due to the modulation geometry a grating set-up is sensitive to SAS in one dimension only. That makes it equivalent to other techniques in this angular regime such as slit collimated SAS instruments2, Bonse Hart cameras33 but also spin-echo small angle neutron scattering (SESANS)34 measuring what is referred to as slit-smeared SAS2,34. Hence, the well-known limitations of modeling and data analyses apply2. This is characteristic of the technique itself and implies, that scattering systems, which display ordering of anisotropic structures, i.e. which produce asymmetric scattering patterns in 2D, require special attention concerning sample orientation and might limit the ability of structural analyses especially without rotating the sample2,24,34. Note that this by no means implies that the method(s) are limited to isotropic particle or structure shapes2. However, it also implies that the scattering geometry that has to be taken into account here can be restricted to one dimension and corresponding scattering and correlation functions represent projections of the 2D functions onto a single axis (perpendicular to the beam and in modulation direction) as is described in detail in2,34.

In order to derive a general solution, a relation between conventional scattering theory and dark-field contrast imaging parameters can be found when describing the scattering angle θ, for which in the SAS approximation sinθ~θ~tanθ, as

respectively. Consequently one can express the scattering vector q not only in terms of the scattering angle θ but also in terms of the position-shift x of the interference pattern at a specific sample to detector distance Ls in a grating measurement as

The position shift x corresponds to a phase shift Δω of the modulation function of

where first x is substituted by Lsθ, then 2πθ by qλ and finally by .

Consequently we find what has earlier been referred to as the autocorrelation length of a grating set-up27

as simply defined by geometric considerations. Note that that is hence a general case and not limited to spatial beam modulation by a grating interferometer set-up. Note that L's given by the relation L's = (L1 + L2-Ls)L2/L1 is required for calculating ξGI in case the sample is positioned between source (grating) and phase grating, with the distances between those given by L1 and between phase grating and analyser grating (detector) by L2. This corresponds to the findings by Donath et al.35 for the sensitivity of the grating interferometer in different geometries. When the sample is placed upstream the phase grating in the plane wave case, where no source grating is used, L's is simply replaced by the distance L2 between phase and analyser grating because for and with the definition L2 = mp2/λ follows that with m being the Talbot order21 just like applied in Ref. 21,24. This way, however, only discrete values of Ls can be probed and an intrinsic connection with the Talbot effect rather than a dependence on geometric conditions only is implied.

Having established a correlation between the induced phase shift Δω of scattering to a specific angle θ, the auto-correlation length and the modulus of the scattering vector q, it is important to understand how scattering and a specific scattering function impact the visibility measured with a grating interferometer set-up. The visibility V is defined as V = (Imax-Imin)/(Imax + Imin) of the measured intensity I, which is spatially modulated corresponding to the interference pattern introduced by the phase grating at a specific Talbot distance at which it is detected5. While radiation which is not scattered (θ0 = 0) and therefore arrives with Δω = 0 contributes at a maximum to the visibility V, as its particular visibility V = V0, radiation which is scattered to a specific angle θ, i.e. with a specific q and hence a specific phase shift obviously contributes less. Consequently a degradation of the visibility is introduced, by scattered radiation producing a visibility V<V0. Given that the scattering function is symmetric around its center at q0 = 0 = θ0, which is a general assumption of SAS, i.e. scattering to θ means equal scattering to -θ or S(q) = S(-q) and with the basic relation

that is valid for all points of the modulation function (Fig. 2) as

the visibility can be expressed as

Taking into account the whole scattering function S(q) and that the final visibility is a result of the convolution of the scattering function with the modulation function7,26,29 of the grating interferometer this transforms into

Given the fact that the scattering function S(q) is a kind of Fourier transform of the real space correlation function,

and hence

the normalized visibility can be put as

being directly proportional to the real space correlation function.

Figure 2
figure 2

Illustration of the modulation term and the basic cosine relations by an undisturbed modulation term of the instrument response function like in an ideal empty beam measurement (blue line), a modulation term according to equ. (7) like assuming scattering causing a phase shift Δω of +/- π/5 (orange line) coinciding with the sum (dots) of half “intensity” modulations shifted in phase to π/5 and -π/5 like illustrated by gray dashed lines.

Full size image

This result means, that grating based and in general cosine modulation based (dark-field) SAS measurements36, perform a back-transformation of the scattering function into real space and hence allow direct measuring of the real space correlation function of a system.

However, the measured signal might also contain un-scattered radiation. In order to account for that the macroscopic scattering cross section and the sample thickness t have to be taken into account and with defining the fraction of scattered radiation

This situation and solution can be found equivalent to that of the well-known and well described spin-echo small-angle neutron scattering (SESANS)37, where the response function can be written as a cosine dependence of the beam polarization, rather than a spatial function, on with being the auto-correlation length of such set-ups referred to as spin-echo length37. It can be shown, as has been shown for SESANS, that taking into account multiple scattering leads to38

Evidently the simple multiplication with the sample thickness is only valid for a homogeneous sample, which one might assume in a SAS experiment but not so much for samples investigated in imaging, where such multiplication hence has to be replaced by the common integral along a specific path of the beam through the sample as

with and G being position dependent functions.

This establishes a complete description of the dark-field signal and its constitution, by replacing previously used so-called material dependent constants referred to as linear diffusion coefficient26,29 and random Gaussian distributions describing scattering phenomenological by well defined and established material parameters like the macroscopic scattering cross section and the real space correlation function. The latter finally provides the direct correlation of the signal with the structural parameters of the scattering structures, which is fundamental for every scattering method, but could not be established before for grating based dark-field contrast. The equivalence of the solution with the one found for SESANS allows for directly applying modeling and analyses tools developed and described for this technique. In particular, the considerations and calculations provided in Ref. 34 can be directly applied to the case addressed here. In this reference Andersen et al. translate many of the so-called form factors for conventional SAS, describing spheres, cylinders, spheroids etc. for the given case and some theoretical and model distributions are shown in order to highlight the applicability for the study of anisotropic density distributions. This further implies that such approach allows for applying grating interferometers not only for imaging applications but also as a powerful tool for conventional SAS studies especially in the ultra small angle regime utilizing the orders of magnitude of efficiency gain previously restricted to imaging applications only. This in turn enables multiscale measurements bridging Fourier space and real space methods with low brilliance lab based x-ray and with neutron sources.

In addition, this solution for grating based dark-field measurements implies that can even be reconstructed for a tomography for every correlation length probed and hence the function can be retrieved for any position (x,y,z) in the sample corresponding to the spatial resolution of the set-up (voxel). This corresponds to a 3D resolved quantitative SAS measurement in case the tomography is performed for a sufficient number of correlation length values.

Discussion

In order to demonstrate the potential of this approach an example shall be given. Assuming a specimen of diluted hard spheres with radius r, for which the real space correlation function, like many others, is well known from SESANS39 being

and which has been stressed earlier27,28,29, allows comparing the theory presented here with calculations and measurements presented in Ref. 27. For that purpose the data presented in Fig. 3a (from Fig. 4 in Ref. 27) is extracted and sorted by sample, i.e. different radii r of spherical SiO2 particles measured in a dispersion of H2O and by autocorrelation lengths used for the specific measurements like given in Ref. 27. This data27 μd′(r,ξGI) is multiplied by the autocorrelation length ξGI in order to get a correspondence with the function 2r(G(ξGI)-1) in the description derived here. Fig. 3a also demonstrates, that the calculation and data presented in Ref. 27 corresponds to 2r|G(ξGI)-1|/ξGI. In the presented theory the factor r is an integral part of the macroscopic scattering cross section Σ for spherical particles which is defined as

Other parts of Σ like the scattering length density contrast Δρ, wavelength λ and volume fraction φV on the other hand are not taken into account as they have been normalized with in Ref. 27 according to equ. d71 ibid. With these values a normalized visibility corresponding between the theory here and the data extracted from Ref. 27 is achieved with

and the results of both are plotted in Fig. 2b as a function of ξGI. A very good agreement is found, which proves that the theory very well describes the measurements. Furthermore, it is clearly visualized that important sample characteristics can not only be quantified, but easily be read from the data in particular for such kind of structure. The autocorrelation value at the saturation point, i.e. where the visibility does not decrease anymore with increasing autocorrelation length, directly provides the diameter of the hard spheres responsible for the scattering signal. This can already be seen from the transformation performed in Fig. 3a as compared to the representation in Ref. 27. At 2r/ξGI ≤ 1, |G(ξGI ≥ 2r)-1| = 1. On the other hand it is obvious, that the visibility value of the saturation is directly related to the macroscopic scattering cross section Σ of the system, i.e. to the volume fraction of the particles and the scattering length density contrast. That means at ξGI = 2r the visibility value stabilizes at. The information content of such measurement is equivalent to that of a conventional SAS measurement, however, spatial resolution is achieved without the requirement of scanning a pencil beam, like in conventional SAS experiments aiming for macroscopic 2D spatial resolution.

Figure 3
figure 3

Data versus theory (a) Representation of measured data μd’ and calculation as provided in Ref. 27 (blue line and symbols); Data and theory transformed according to ξGI μd’/2r (red crosses and green line with circles, respectively) and |(G-1)| as calculated for the samples from the theory presented here (red line) displaying full agreement proving that the calculation presented and data reduction in Ref. 27 corresponds to 2r|(G-1)|/ξGI; (b) Visibility data (markers) from (a) Ref. 27 and calculation (lines) presented according to equ. (18) as a function of autocorrelation length ξGI and sorted by sample (particle size), demonstrating good agreement between theory and data as well as the direct relation to particle size and scattering cross section (note: here represented by 2r only), both of which can be extracted straightforwardly. (Note: no error bars are given as original data in Ref. 27 is provided without error bars and any additional introduced error is considered less than the given symbol sizes).

Full size image

Figure 3b also illustrates, how the contrast achieved depends on the specific autocorrelation length at which a single measurement is performed and hence that the dark-field contrast between different sized scattering particles can potentially be even inverse when measured at a different autocorrelation length e.g. at different set-ups. That implies that the contrast of dark-field images can significantly be influenced by the choice of the parameters defining the autocorrelation length, like the wavelength, the sample to detector distance and the used period of the interference pattern. Therefore even in qualitative measurements significant care has to be taken of the use of the corresponding parameters, because otherwise severe misinterpretations and discrepancies between measurements might be caused. The specific shape of scattering structures defines the contrast behavior in dependence on the set autocorrelation length34 and the concentration and scattering length densities define the saturation of the dark-field signal at the autocorrelation length corresponding to the longest correlation length in the sample, i.e. the maximum dimension of the structure. Nearest neighbor correlations when resolved for example in systems with high concentrations and giving rise to what is referred to as structure factor in SAS will cause further modulation of the signal at corresponding longer autocorrelation lengths34,39.

Not only in this respect it is certainly worth considering the work by W. Yashiro et al. in Ref. 24, where a strongly anisotropic structure is investigated with grating interferometry. In particular the measured points for a sample orientation of φ = 15° and the point at = 4 μm (note is expressed as “pd”) are most noteworthy (Fig. 5a in Ref. 24). Taking into account next neighbor correlations (a structure factor in terms of SAS) like described in Ref. 34, 39, i.e. pair correlations apart from the real space correlation of an isolated shape of a scattering structure (a form factor in SAS), but also the tomographic representation of bigger structures in the same sample (fig. 9 in Ref. 24), it must seem obvious that such next neighbor correlation has been measured here and the particular deviations from the presented fit are not just an artifact. In the approach presented in Ref. 24 and Ref. 21, the autocorrelation length is described as the product of what is referred to as the Talbot order and the modulation period. While this is equivalent to the purely geometric description provided here for the particular set-up used in these works, it seems to limit probing this parameter to a few distinct values. Though the approach has lead via extensive wave calculations to the conclusion that the visibility as a function of “should be related to the Fourier transform”21 of the angular scattering function and a corresponding description and interpretation of such function in terms of real space correlation functions of structures, no reliable specific shapes and dimensions of scattering structures could be provided. Such can only be achieved, in the light of the here presented general and extensive approach, by probing a sufficient number of values and applying model fits equivalent to procedures applied in SAS. For the cases presented in Ref. 21 and 24 that would imply to place the sample between the phase and analyzer grating, which themselves are set to a high Talbot order and scanning the distance of the sample to the analyzer grating. Subsequently the models that are described in Ref. 34 and 39 can be fitted according to the presented analogy of methods and will provide values for diameters, shapes and orientations as well as next neighbor distances just like in corresponding SAS or SESANS studies. Like described in Ref. 34 only in cases where no a priori knowledge about the sample structures can be applied and is obvious from the measurements, a sum of Gaussians like proposed in Ref. 21 might be the most viable option for data fitting. Even in such cases the average structure size can be directly extracted from the measured visibility function34, though also the principle of Guinier analyses and Porod's law2,34 is readily available for corresponding data analyses.

In conclusion a quantitative and general relation between the measured visibility in grating interferometer based dark-field contrast imaging and the specific sample parameters of scattering cross section and in particular the real space correlation function of the structures in the sample that contribute to small-angle scattering and hence the dark-field signal has been derived. It has been demonstrated how a scan of the autocorrelation length of the set-up in a dark-field contrast measurement yields the corresponding parameters and hence 2D SAS measurements become possible in such imaging mode providing the potential of full quantification of scattering parameters and consequently full structural characterization. The equivalence with a well known neutron scattering method, namely SESANS has been demonstrated, which in turn allows to build on the well know scattering functions, i.e. real space correlation functions, derived for this method in literature. Additionally, the presented theory underlines the potential of tomographic measurements, which allow obtaining corresponding information with 3D spatial resolution. This theoretical assessment of the dark-field signal bears the potential to revolutionize the application of dark-field imaging, which already now as a qualitative tool is highly successful with x-rays as well as with neutrons. The knowledge of its quantitative character will without any doubt open numerous new fields in many areas of material science exploiting the outstanding efficiency for spatial resolved SAS investigations. And finally the generality of the approach and solution implies that it applies to and allows for other techniques of sinusoidal beam modulation to be developed and exploited for SAS and eventually for spatially resolved fully quantitative SAS studies.