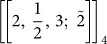Introduction

Quantum error correction is of great importance to quantum computational technologies because it provides the primary tool known as quantum error-correcting code (QECC)4,5,6,7,8,9,10,11,12, for combating the inevitable and ubiquitous quantum noise. Entanglement is an essential resource for many quantum computational and communication processes13,14,15,16. The entanglement-assisted quantum error-correcting code (EAQECC)1,17,18 is a remarkable breakthrough that combines these two concepts by introducing pre-shared maximally entangled pairs, called ebits, between the encoder (Alice) and the decoder (Bob) in the communication scenario. All qudits possessed by Bob suffer no errors because they do not undergo any communication from the beginning to the end (quantum memories are assumed to be noiseless). The advantages of EAQECC lie in its simplified construction, involving primarily classical linear codes without the self-dual requirement, and, more surprisingly, in its improvement of the encoding rate over that of the standard QECC2.

By the notation [[n, k, d; m]]p, where p is the dimension of the physical qudits, we mean the following EAQECC protocol: Alice possesses n qudits and Bob possesses m qudits. Initially, each qudit of Bob's is maximally entangled with one of Alice's qudits. Alice encodes k logical qudits into n physical qudits so that an arbitrary error on up to qudits can be corrected and then sends all her qudits through noisy quantum channels (in this paper, quantum channels are used for quantum communication only; hence, a noisy or noiseless channel only means the communication will be noisy or noiseless) to Bob. After receiving these n qudits, Bob performs error correction on all qudits he has, including those m qudits that suffer no errors. As one can observe, a crucial assumption in the EAQECC protocol in the communication scenario is that the ebits shared by Alice and Bob pre-exist non-locally. In other words, either the ebits can be prepared non-locally or there exist some noiseless quantum channels through which locally prepared ebits can be communicated. However, noiseless quantum communication does not exist in practice. To prepare ebits non-locally, entanglement distillation3,4 or similar processing is needed, which requires the consumption of additional resources and hence, significantly reduces the code's efficiency19,20. Therefore, considering the preparation of ebits, the disadvantages of the protocol may outweigh its advantages, becoming a serious drawback of the EAQECCs.

By a more feasible EAQECC protocol, we mean a protocol in which (I) no additional resources are consumed other than those required by the encoding and decoding, (II) all ebits are prepared locally and (III) all quantum channels are generally noisy. Does such a protocol even exist? The answer is in the affirmative provided that two-way noisy communication (2WNC) is allowed, i.e., Bob and Alice can exchange qudits via noisy channels. Before introducing this protocol, first of all we shall make two common assumptions: (I) quantum noise affects each qudit independently and (II) only noise in quantum communication (communication errors) is considered, while quantum memories and the encoding-decoding process are noiseless. In other words, we assume that neither storage errors nor encoding-decoding errors occur.

As we all know, the original EAQECC protocol is equivalent to allowing a one-way noiseless communication from Bob to Alice, the pre-sharing of the ebits, encoding and a one-way noisy communication from Alice to Bob. By comparison, in our 2WNC-assisted protocol, the noiseless communication from Bob to Alice is replaced by a generally noisy communication. That is to say, errors may occur before encoding, which renders the ebits not perfectly entangled any more. It is well-known that a pre-encoding error will spread throughout the encoding circuit; however, what it finally evolves into after encoding is uncertain because the same code can be implemented using different encoding circuits. Therefore, the key problem of applying the 2WNC is to correct the pre-encoding errors without consuming additional resources, which will be successfully solved in this paper.

Results

Implementing the EAQECC [[4, 1, 3; 1]] with two-way noisy communication

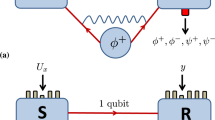
The most famous example of EAQECC is the binary [[4, 1, 3; 1]]2 code proposed by T. A. Brun et al.1. In fact, EAQECC [[4, 1, 3; 1]]p exists for all p ≥ 2 and the corresponding protocol is depicted schematically in FIG. 1a. Because it requires the ideal nonlocal sharing of ebits or the assumption of noiseless channels, this protocol is technically hard to implement. As the first example, we implement the code [[4, 1, 3; 1]]p with p = 4 in a more feasible manner, i.e., without consuming additional resources for the non-local sharing of ebits.

Figure 1
figure 1

A comparison of (a). the EAQECC protocol [[4, 1, 3; 1]] and (b). our 2WNC-assisted QECC protocol .

Bob's part and Alice's part are horizontally separated by a grey line and the flow of time is from left to right. The dotted lines represent noisy quantum channels. A pair of grey circles represents two qudits in a maximally entangled states that are pre-shared non-locally by Alice and Bob and a grey ellipse represents a qudit composed of two subsystems in a maximally entangled state.

Full size image

We consider the following protocol: (I) Alice and Bob possess four and one 4-level qudits, respectively. Because a p2-level qudit can always be regarded as the composite of two p-level subsystems, Bob uses two qubits to represent his 4-level qudit. (II) After locally preparing his two qubits into a maximally entangled state, Bob sends one qubit, the flying qubit, to Alice through a noisy quantum channel and keeps the other qubit, the idle qubit, which suffers no errors, for himself. (III) After receiving the flying qubit, Alice performs the encoding on all qudits that she possesses (one qubit and four 4-level qudits). (IV) Then, Alice sends all of her qudits to Bob through noisy quantum channels. (V) Together with the idle qubit, Bob performs the error correction on all five 4-level qudits. A comparison between our 2WNC-assisted QECC protocol and the EAQECC protocol is presented in FIG. 1. It is evident that in our protocol, the 4-level qudit that was initially possessed by Bob is “partially noisy”: the idle qubit suffers no errors, whereas the flying qubit may suffer two different types of errors, i.e., pre-encoding and post-encoding errors.

Suppose the error rate for a noisy channel is r. Because the quantum noise affects each qudit independently, the probability of the simultaneous occurrence of both a pre-encoding and a post-encoding error on the flying qubit, as well as that of the simultaneous occurrence of a pre-encoding error and an arbitrary error on one of the other four 4-level qudits, is obviously of order , which approximates the probability of a two-qudit error. Hence, the pre-encoding and post-encoding errors can be regarded as independent single-qudit errors. As long as all single-qudit errors can be corrected, the aforementioned protocol yields a code, where represents the “partially noisy” qudits that initially belong to Bob. As mentioned before, a pre-encoding error will spread throughout the encoding circuit and evolve into a multi-qudit error after encoding; hence, the code we construct should be capable of correcting those multi-qudit errors that correspond to the pre-encoding errors of the flying qubit. The stabilizer detailed in Table 1 defines such a code that can correct all the aforementioned errors. Here, each 4-level qudit is regarded as a composite of two qubits. The bit-flip and phase-flip operators of a qubit are denoted by X = |1〉〈0| + |0〉〈1| and Z = |0〉〈0| − |1〉〈1|, respectively and Y = iZX. Then, a 16-element group {〈X, Z〉 ⊗ 〈X′, Z′〉} — with X ⊗ I′, Z ⊗ I′, I ⊗ X′ and I ⊗ Z′ being the generators and the overall factor being dropped — forms an error basis of the 4-level qudit, where subgroups 〈X, Z〉 and 〈X′, Z′〉 refer to the error basis of the two subsystems, respectively.

Table 1 The stabilizer of the 2WNC-assisted QECC . Qudits 1, 2, 3, and 4 belong to Alice, and qudit 0 belongs to Bob. Because there are eight generators of the stabilizers, any error exhibits an 8-bit syndrome, a binary vector with entries 0 and 1 denoting whether the error is commuting or anticommuting with the corresponding generators. For each 4-level qudit, the left-hand column, the right-hand column and the sum of the two columns represent the syndromes of the errors on the first qubit, second quibit and both qubits, respectively, all of which collectively form the error syndromes of the coresponding 4-level qudit. For example, the syndrome of a single-qudit error on qudit 2 is View full size image
Full size table

From the stabilizer, one can observe that for each of qudits 1, 2, 3 and 4, the 15 possible single-qudit errors have different syndromes. For qudit 0, the second qubit is the flying qubit; thus, the right-hand column represents the syndromes of the post-encoding errors on this qubit, which also differ. For the encoding circuit illustrated in FIG. 2a, the pre-encoding bit-flip error and phase-flip error evolve into multi-qudit errors as and , respectively, after encoding; thus, . According to the stabilizer, the syndromes of these multi-qudit errors are also different. Therefore, the stabilizer truly defines a 2WNC-assisted QECC . See the Supplemental Material for complete details. As one can observe, in our protocol, the forwards noisy communication (from Bob's point of view) leaves the maximally entangled pair of idle and flying qubits prepared by Bob noisy. However, after the backwards communication, because the correction of the pre-encoding errors actually purifies the noisy entangled pairs, our protocol successfully combines the entanglement distillation into the process of error correction. Meanwhile, no additional resources are consumed; more importantly, neither non-local operations nor noiseless quantum channels are required. Hence our protocol truly implements the EAQECC [[4, 1, 3; 1]]4 in a more easily realisable way.

Figure 2
figure 2

The encoding circuits of the 2WNC-assisted QECCs (a). and (b). .

A boxed H represents a Hadamard gate, a pair of connected black dots represents the controlled-phase gate UCP, a pair of connected black (source) and white (target) dots represents a controlled-NOT gate UCN and . The dotted lines represent noisy quantum channels.

Full size image

The 2WNC-assisted QECC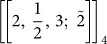

We propose a novel QECC protocol to implement the well-known EAQECC [[4, 1, 3; 1]] in a more feasible manner with the assistance of two-way noisy communication. In our protocol, the qudit possessed by Bob partially suffers errors before and after encoding, whereas in the original protocol, it is completely error-free. In other words, codes based on our protocol handle more errors and hence can not be more efficient than the corresponding original EAQECCs, which appears to be the price that must be paid for “easier implementation”. It is clear that is an appropriate measure of the encoding rate for our 2WNC-assisted code , which means that our protocol is as efficient as the standard QECC protocol [[5, 1, 3]]4. Hence, a second question arises: can our 2WNC protocols improve the codes' efficiency over standard QECC protocols in some sense? Our second challenge is to construct a 2WNC-assisted QECC that offers a higher encoding rate than the standard QECC using the same amount of resources, e.g., the same number of physical qudits.

In standard quantum error correction, it is well-known that four qudits are insufficient for the construction of any valid 1-error-correcting codes, becasuse they can only encode, at maximum, a one-dimensional subspace of distance 3. In other words, no quantum information can be encoded in code [[4, 0, 3]]p, for an arbitrary value of p. However, the following QECC protocol assisted by 2WNC allows four qudits to encode information: (I) Both Alice and Bob possess two 4-level qudits. (II) After representing each of his two 4-level qudits by a pair of maximally entangled qubits, Bob chooses one qubit from each pair and sends them to Alice through noisy quantum channels. (III) Alice receives these two flying qubits and performs the encoding together with the two 4-level qudits she possesses. (IV) Alice sends all of her qudits (two qubits and two 4-level qudits) to Bob through noisy quantum channels. (V) Together with the other two idle qubits he holds, Bob undergoes the process of error correction and decoding. Via this protocol, Alice can send Bob one-qubit of information, i.e., two logical states. Therefore, a valid 1-error-correcting code with parameters of , where the dimension of the logical subspace is represented by , is possible using the stabilizer detailed in Table 2.

Table 2 The stabilizer of the 2WNC-assisted QECC . Qudits 2 and 3 belong to Alice, and qudits 0 and 1 belong to Bob. For each of the qudits 0 and 1, the second qubit is the flying qubit. The existence of seven generators for the stabilizer means that one logical qubit is encoded
Full size table

The syndromes of all single-qudit errors are listed in the Supplemental Material, indicating that for qudits 2 and 3, each single-qudit error has a different syndrome except the two errors and . Fortunately, forms a stabilizer such that these two errors could also be corrected. The encoding circuit for the code is illustrated in FIG. 2b, indicating that the 6 pre-encoding errors evolve into multi-qudit errors after encoding as follows: , , , , and . According to the stabilizer, when these errors are considered along with the 6 post-encoding errors, all 12 errors lead to different syndromes. Therefore, our stabilizer truly defines a 2WNC-assisted QECC . More details are provided in the Supplemental Material.

Discussion

This paper proposes a QECC protocol assisted by two-way noisy communication to overcome the serious drawback on the implementation of EAQECC protocols, namely, the requirement for pre-shared maximally entangled pairs. Because of their capability of correcting pre-encoding errors, our encodings can achieve entanglement distillation and error correction simultaneously. Ref. 20 also provided a protocol that could combine the distillation into the process of error correction, the idea of which is that implementing a standard code [[n + m, k, d]] is, in other words, realising distillation and error correction simultaneously for the EAQECC [[n, k, d; m]]. Therefore, their protocol can not be more efficient than the standard QECC protocol. Whereas, in our 2WNC-assisted protocol, the encoding rate can be improved over that of the standard QECC protocol.

Usually, three types of errors exist in practice, i.e., communication errors, storage errors and encoding-decoding errors. Here, we have considered communication errors only. The case in which storage errors arise on the idle qudits has been discussed in Refs. 20, 21. However, as yet, there have been no efforts directed towards overcoming encoding errors, which is quite a complicated and difficult topic that is worth further exploration.

Methods

In our 2WNC-assisted QECC protocol, we must combat pre-encoding errors. As mentioned before, a stabilizer code can be implemented using different encoding circuits; and, the evolution of a pre-encoding error is circuit-dependent even if the stabilizer is fixed, rendering the correction of pre-encoding errors the most difficult task in the construction of 2WNC-assisted codes. Thus, a certain challenge appears to be unavoidable: does a systematic method exist for the construction of 2WNC-assisted QECCs? The answer is that, indeed, one does.

Construction

Consider a p2-level “partially noisy” qudit composed of two p-level qudits, a flying qudit and an idle qudit. Let |l〉 be the computational basis of the p-level qudit and take and . If both the flying and idle qudits are prepared in the state , we obtain a maximally entangled state after a controlled-phase gate . The error basis of this qudit can be written as {〈X, Z〉 ⊗ 〈X′, Z′〉}, where , and the primed operators refer to those of the flying qudit.

Denote the initial state of the entire system by , where |t〉 is the initial state of the remaining qudits and denote the encoding operator by U. After encoding, the pre-encoding errors 〈X′, Z′〉 will evolve into multi-qudit errors 〈ξX′ = UX′U†, ξZ′ = UZ′U†〉for the given encoding circuit. If there were no pre-encoding errors, the codeword would read |c〉 = U|Ψ〉. When a pre-encoding error X′ arises, we obtain U[X′|Ψ〉] = ξX′|c〉. On the other hand, because of the identity X′UCP = Z†UCPX′, we have , where the second equality arises from [〈X, Z〉, U] = 0 and . Finally, we obtain ξX′|c〉 = Z†|c〉, indicating that the error ξX′ behaves exactly like a Z† error on the idle qudit. Similarly, we also have ξZ′|c〉 = X†|c〉, rendering the syndrome set 〈S(ξX′), S(ξZ′)〉 for the pre-encoding errors on the flying qudit being identical to the syndrome set 〈S(X), S(Z)〉 for the errors on the idle qudit.

Therefore, with the assistance of entanglement between the flying and idle qudits, the problem of correcting the pre-encoding errors on the flying qudits is reduced to that of correcting the errors on the corresponding idle qudits. In other words, entanglement renders the pre-encoding error syndromes independent of the encoding circuit and allows for systematic code construction. That is, constructing a 2WNC-assisted QECC is equivalent to constructing a stabilizer QECC over mixed alphabets22 with parameters of and then transforming its encoding circuit into a standard form, in which the encoding operator acts trivially on the idle qudits (see the Supplemental Material for the technical details). Systematic methods based on graph states23,24,25 and coding clique26,27 exist for the construction of mixed-alphabet QECCs. This work considers only a special 2-alphabet case, whose details of the construction are provided in the Supplemental Material.

Discussion

At this point, one may ask the following question: if an equivalent mixed-alphabet construction exists, why do we need the 2WNC? First, in the sense of quantum communication, our 2WNC-assisted protocol truly brings benefits over the corresponding mixed-alphabet protocol : (I) in our scenario, only n + m qudits (np2-level qudits and mp-level qudits) are involved in the process of communication, whereas in the mixed-alphabet scenario, n + 2m qudits (np2-level qudits and 2mp-level qudits) are involved; (II) although the flying qudits are communicated twice in our scenario, no information is carried in the forwards communication (from Bob to Alice), whereas in the mixed-alphabet scenario, information is encoded in all n + 2m qudits. Based on these two points, our 2WNC-assisted protocol explicitly economizes m-qudit of resources for communication. Second, when we use two p-level qudits to represent a p2-level particle, the single-qudit errors for this particle then include errors on the flying qudit, errors on the idle qudit and errors on both qudits. If we initially place both the flying and idle qudits on Alice's side, only when we know the physical details of how the flying and idle qudits compose the p2-level particle and how the quantum channels affect them such that we know in advance that among these three types of errors, the errors on both the flying and idle qudits are much smaller, can we have the equivalence. However, in general, that information is lacking; hence, only a standard code is available.

As one can observe, in our two examples and , each 4-level qudit is treated as a composite of two qubits, which is actually an unnecessary requirement for Alice's qudits (qudits 1, 2, 3, 4 in the first example and qudits 2, 3 in the second example) because our two codes are equivalent to the mix-alphabet codes and , respectively. However, we are lacking of the technologies of drawing encoding circuits for mixed-alphabet systems; hence, in order to obtain the encoding circuits, each of Alice's 4-level qudits has to be represented by the composite of two qubits as well. As long as all 15 possible errors of a 4-level qudit can be corrected, the basis transformation is reasonable.