Introduction

Most abundant among heavy non-volatile elements in the Universe, iron has been extensively studied in its solid and liquid forms. Where experiments are not feasible, computer modeling is used to understand properties of liquid iron at high temperature and pressure (see, e.g., Ref. 1) at which iron exists in the core of planets such as Earth as well as giants such as Jupiter. It is worth to note that even the location of melting line of iron is not well established from experiment, but computer simulation helps to clarify the experimental results2. Little is known about iron properties in the supercritical region because iron's critical point is located at severe (P,T) conditions. Yet here, in the supercritical state, many interesting surprises await, including the contemplated percolation-driven metal-insulator transition (for review, see, e. g., Ref. 4, 5) and recently proposed dynamic, thermodynamic and structural transitions6,7,8,9,10,11,12,13.

Until recently, it has been held that no difference between a gas and a liquid exists above the critical point. Instead, the supercritical state has been viewed as qualitatively the same everywhere on the phase diagram, with no distinct changes of properties with varying pressure and temperature17. Yet the idea that the boiling line can be meaningfully extended above the critical point has been long intriguing. For example, the Widom line, the line of maxima of correlation length6, continues in the supercritical region and vanishes not far above the critical point. In this approach, a short bunch of lines, each corresponding to lines of maxima of different physical properties such as heat capacity, compressibility, thermal expansion and so on, starts from the critical point and ends quite close to it18,19. The alternative demarcation of the supercritical state, the Frenkel line, is not related to the existence of the critical point9 and separates two physically distinct states at arbitrarily high pressure and temperature above the critical point8,9,10,11,12,13.

The main idea behind the Frenkel line (FL) is that regardless of how far one is above the critical point, the crucial difference in atomic dynamics can still be ascertained. Accordingly, the FL demarcates the transition between the liquid-like regime where particle dynamics consists of both oscillations and ballistic jumps between quasi-equilibrium positions and the gas-like regime where the oscillatory component is lost and the motion is purely ballistic as in the gas. This change in dynamics leads to a dramatic change of all major system properties, including diffusion, viscosity, thermal conductivity, speed of sound, specific heat, structure as well as the ability to maintain solid-like shear modes at any frequency8,9,10,11,12. Since the existence of shear modes is associated with rigidity, the transition at the FL is the transition between the “rigid” liquid and “non-rigid” gas-like fluid.

One can estimate the location of the Frenkel line by observing a change in microscopic dynamics of the particles of a fluid. As was firstly pointed out by Frenkel21, in low temperature fluid the particles make few oscillations in a cage of other particles and then jump into another cage. In high temperature fluid the oscillatory motion does not present. The particles move by jumps until collision with other particles. The presence or absence of oscillatory component in the particle movement can be qualified from the velocity autocorrelation function (VAF). If the particles oscillate then VAF also oscillates. It gives a convenient method to evaluate the location of the FL microscopically: the change of dynamics at the FL can be unambiguously quantified by the disappearance of the minima in the velocity autocorrelation function, signalling the loss of oscillatory component of motion9.

The FL has been calculated for model systems such as Lennard-Jones (LJ) and soft-sphere liquids9,10,11,12,13. An important question is whether one can propose a general and simple recipe for drawing the FL on the phase diagram for any liquid, without detailed system-specific calculations. In this paper, we answer this question positively and use iron, with its non-trivial many-body interactions, as an important case study. We subsequently discuss the relationship between the FL and percolation transition in supercritical fluids as well as transitions between conducting and insulating states. We finally point the relevance of our results to the evolution of iron conductivity and emergence of magnetic fields in planets and exoplanets at various stages of their evolution.

A representative example of the velocity-autocorrelation function (VAF) is shown in Fig. 1a. We observe the transition between two regimes with and without minima of the VAF, corresponding to the loss of the oscillatory component of atomic motion9. This transition defines a point at the FL in (P,T) or (ρ,T) coordinates, where P is pressure and ρ is density.

Figure 1
figure 1

(a) Velocity autocorrelation functions for iron at ρ = 10 g/cm3 and different temperatures. The inset enlarges the oscillating part of the plot. (b) Heat capacity of iron at the same density (Color online).

Full size image

It is important to note that FL corresponds to the loss of transverse excitations of fluid while longitudinal excitation are preserved. One can see the loss of transverse excitations by means of positive sound dispersion (PSD). PSD was observed in experiment and simulations of liquid argon at relatively low temperatures while at high temperatures it disappears14,15. In our previous publications it was shown that the temperature of PSD disappearance corresponds to the temperature where the oscillatory component of VAF is lost11.

In addition to the dynamic VAF criterion, the FL can be located using the thermodynamic criterion: cv = 2 (kB = 1). Indeed, liquids support solid-like shear modes at frequency , where τ is liquid relaxation time, the average time between atomic jumps at one point in space21. As discussed above, the FL corresponds to the loss of oscillatory component of motion and τ ≈ τD (τD is the shortest vibration period), implying that the system loses its ability to support shear modes at all available frequencies. The loss of oscillatory component of the particle motion implies the loss of oscillations of VAF. The heat capacity of crystal is 3 (DulongPetit law). Heat capacity of a liquid close to the melting line is also close to this value. The system energy in the absence of transverse excitations is 2NT ( kinetic energy and potential energy of the remaining longitudinal mode) and therefore cv = 222. It is important to note that here we neglect the anharmonic effects. Although it is not very precise, it does not alter the qualitative behavior of the system. In Fig. 1b, we show a representative cv, calculated as temperature derivative of the energy along an isochore.

Although some approximations are involved, phonon theory of heat capacity of liquids gives excellent agreement with experiment23,24

In Fig. 2, we show the FL calculated using both dynamic and thermodynamic criteria and find a very good agreement between the two calculations. This serves as an important self-consistency check. The agreement is similar to that we observed earlier for the simple LJ system9.

Figure 2
figure 2

The Frenkel line of iron from two criteria (see the text) in (a) ρ−T and (b) P−T coordinates.

(Color online).

Full size image

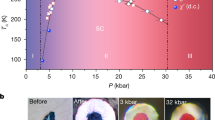
In Fig. 3, we show the FL on the phase diagram together with the melting line and the critical point. The melting line is plotted using the data from previous calculations20 and the critical point is taken as Tc = 9250 K (with uncertainty of 1000 K) and ρc = 2.0 g/cm325,26. The boiling line has been calculated from the law of corresponding states and previous data for the LJ system30. We observe that the FL crosses the boiling line at approximately ρ ≈ 4.5 g/cm3 and T ≈ 6500 K, or 0.7Tc and 2ρc, which in units relative to the critical point is very similar to what was previously found in the LJ system9.

Figure 3
figure 3

Placing Frenkel line on the phase diagram of iron.

Errors in determination of critical point and metal to insulator transition point are of the order of the symbol size. (Color online).

Full size image

Locating the FL for iron is our first result. It immediately enables one to predict the state of the supercritical liquid in several cases of interest. For example, pressure and temperature of iron in the Jupiter core is P = 90 Mbar and T = 3.0 · 104 K34. Using our MD simulations, we have calculated the corresponding density ρ = 15.6 g/cm3. We observe that the location of this point on the phase diagram is below the FL (see Fig. 3), implying that liquid iron in the center of Jupiter core is in the rigid liquid state rather than in the gas-like non-rigid fluid state, with all physical implications for the major properties discussed above. The same is the case for iron in the Earth core which lies even further down from the FL as compared to Jupiter in Fig. 3. This is an important assertion for constructing models of planet interiors and understanding essential effects such as, for example, diffusion, viscosity, convection and thermal conductivity34. Notably, this includes conductivity and generation of magnetic field.

An interesting observation is that the rigid-liquid state of iron in planets corresponds to current conditions only. At the early stages of planet evolution, core temperatures were significantly higher, implying that supercritical iron existed in the gas-like non-rigid fluid state (see Fig. 3) where all major properties are qualitatively different as discussed above. The same applies to younger and hotter exoplanets. We therefore propose that as planets and exoplanets cool off, supercritical iron in the core may undergo the transition at the FL. One important consequence of this transition is related to conductivity and magnetic fields.

We now explore whether the FL can be drawn for any liquid without detailed system-specific simulations such as VAF or cv. There is a theoretical argument that after a certain pressure threshold, the FL should be parallel to the melting line in the double-logarithmic plot. Indeed, at high pressure the intermolecular interaction is reduced to its repulsive part only whereas the cohesive attracting part no longer affects interactions. For the repulsive potential (so called soft spheres system) scaling of pressure and temperature is well-known: system properties depend only on the combination of T Pγ, where γ is uniquely related to n. Consequently, T Pγ = const on all (P,T) lines where the dynamics of particles changes qualitatively. The qualitative change of dynamics takes place on both FL and melting lines. Therefore, the FL and melting lines are parallel to each other in the double-logarithmic plot. This has been ascertained in direct simulations for the simple LJ liquid9,10.

The important question is whether the parallelism of the FL and melting lines exists for systems where interactions are not reduced to pair power-law interactions. Iron is an important system in this respect: the embedded-atom potential we use20 includes many-body terms so that the energy of interaction between an atomic pair depends on the location of many other atoms. Importantly, we observe in Figure 2 that the FL and the melting lines are parallel in the double-logarithmic plot. This implies that as far as scaling is concerned, interactions can be well approximated by power-law dependence in a fairly large pressure and temperature range despite the apparent complexity of interactions as in iron29.

Combined with the earlier results for the LJ and other simple systems9, this result enables us to propose a simple and general way to locate the FL: it starts slightly below the critical point (slightly below as mentioned above) and runs parallel to the melting line at high pressure limit. We note at this point that by its nature, the FL is not related to the critical point and its overall existence. Indeed, we have recently shown that the transition at the Frenkel line takes place in the soft-sphere system where no boiling line and critical point exist altogether9.

We now focus on the relationship between the FL and atomic arrangements in iron. Since early proposals31, the structure of liquid metals is considered to be well described by a collection of hard spheres of some effective diameter deff at a given density. Several methods to determine deff were proposed that employ the position of the first peak of structure factor S(k). We find the location of the S(k) first peak along both the FL and the melting line and show the corresponding deff in Fig. 4. We observe that deff decreases with temperature. Interestingly, the packing fraction of spheres, , is constant along both lines (see Fig. 5). We observe that at the melting line, η ≈ 0.5. This is close to the earlier result that melting in the system of hard spheres corresponds to η = 0.4932. This suggests a novel melting criterion: melting corresponds to the packing fraction of hard spheres at the hard-spheres melting line, an insights that warrants further consideration.

Figure 4
figure 4

Diameter of effective hard spheres along the melting line and the Frenkel lines of iron.

(Color online).

Full size image
Figure 5
figure 5

Packing fraction of effective hard spheres along the melting and Frenkel lines of iron, along Frenkel line of LJ fluid and along Frenkel line of soft spheres with n = 12.

(Color online).

Full size image

Importantly, we observe that η ≈ 0.3 at the FL (see Fig. 5). We have used our earlier data for the LJ liquid and soft spheres with n = 129 and have repeated the same procedure for calculating η along the Frenkel line for these systems. In Fig. 5 we observe that similar to iron, η ≈ 0.3 for the LJ liquid at the FL.

In case of soft spheres phase diagram becomes effectively one dimensional. Both melting and Frenkel lines are defined via equations γ = const with . Melting of soft spheres with n = 12 corresponds to γm = 1.1516, while Frenkel line is characterized by γF = 0.577. Barker diameter of soft spheres can be expressed as

From this formula one can see that packing fraction of effective hard spheres is simply proportional to γ and constant along the Frenkel line. The magnitude of η at the Frenkel line is ηF,n = 12 = 0.327 which is also very close to the results for LJ and iron.

The importance of η ≈ 0.3 is that it corresponds to the appearance of the percolating cluster in the system of overlapping spheres4. This coincidence is meaningful in the following sense. Below the FL, the presence of oscillatory component means that atomic clusters can be well-defined and typically exist during liquid relaxation time τ. For example, the recent work identified the abundance of different stable clusters in a high-temperature liquid and further established that the concentration of the tetrahedral clusters at the FL is 15–17%, close to the percolation threshold in the system composed from tetrahedra33. In contrast, above the FL where the oscillatory component of motion is lost and atoms move ballistically as in a gas, the concentration of effective spheres does not reach the percolation limit.

The latter circumstance is important for understanding metal-insulator transitions in liquids. Transition between metallic and insulating liquids can be described in frames of percolating spheres model3,4,5. If the density of spheres is high enough and percolating cluster appears then electrons can move through the whole system. Otherwise, at low densities, gaps appear. One can show that presence of percolating cluster in the fluid guaranties that Mott criterium of metal to insulator transition is satisfied3. So, metallic and insulating states in the liquid emerge at packing fractions above and below the percolating threshold, respectively. It is therefore important that the experimental metal-insulator transition in liquid iron (ρ = 2.8 ± 0.5 g/cm3, T = 6500 ± 1500 K27,28) is located not far from the FL (see Fig. 3). We note that the metal-insulator transition has also been observed in liquid mercury4. Once the FL line in mercury is drawn similarly to that in Fig. 3 and following our general recipe for locating the FL discussed above, the proximity of the FL to the experimental metal-insulator transition becomes apparent4. One should note, however, that due to high degree of ionization nonmetallic state of liquid iron still has quite high conductivity27,28.

We can now assert the state of conductivity of supercritical iron at different pressure and temperature conditions. Using the above density of iron in the core of Jupiter, we calculate η = 0.4 and find that η is above the percolating threshold of 0.3. We therefore predict that iron in the Jupiter core is conducting.

We similarly find that η = 0.5 in the Earth core corresponds to the highly conducting core, the result consistent with current understanding. However, we noted above that in the early hotter Earth, iron in the core could be above the FL and therefore existed in the low conducting state. This has important consequence for understanding of the evolution of the Earth's magnetic field: the magnetic field emerged at early stages of Earth evolution when cooling.

In summary, we proposed a general recipe to locate the Frenkel line in the supercritical region of the phase diagram using iron as an important case study. We discussed the relationship between the FL and the metal-insulator transition in supercritical liquid metals. This enables predicting the conducting state of iron in Jupiter and smaller planets such as Earth. We further discussed the evolution of core conductivity and associated evolution of magnetic fields: as planets and exoplanets cool off, supercritical core undergoes the transition to the rigid-liquid conducting state at the Frenkel line.

Methods

We have used classical molecular dynamics (MD) simulations with 3456 atoms interacting via many-body embedded atom potential20 optimized for the liquid iron. Liquids were first equilibrated for 1 ns in the constant volume and temperature ensemble and subsequently used for production runs in the constant energy ensemble with a smaller-than-usual timestep (0.2 fs) in order to properly resolve the velocity autocorrelation function at high temperature. We have simulated several density and temperature points in significant excess of the critical point.