Abstract
Simultaneous existence of correlation in complementary bases is a fundamental feature of quantum correlation and we show that this characteristic is present in any non-product bipartite state. We propose a measure via mutually unbiased bases to study this feature of quantum correlation and compare it with other measures of quantum correlation for several families of bipartite states.
Similar content being viewed by others
Introduction
Quantum systems can be correlated in ways inaccessible to classical objects. This quantum feature of correlations not only is the key to our understanding of quantum world, but also is essential for the powerful applications of quantum information and quantum computation1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19. In order to characterize the correlation in quantum state, many approaches have been proposed to reveal different aspects of quantum correlation, such as the various measures of entanglement6,7,8,9,10 and the various measures of discord and related measures17,18,19,20,21, etc. It is believed that some aspects of quantum correlation could still exist without the presence of entanglement and these aspects could be revealed via local measurements with respect to some basis of a local system.
The simultaneous existence of complementary correlations in different bases is revealed very early by the Bell's inequalities22. Bell's inequalities quantify quantum correlation via expectation values of local complementary observables. In Ref. 23, the feature of genuine quantum correlation is revealed by defining measures based on invariance under a basis change: for a bipartite quantum state, the classical correlation is the maximal correlation present in a certain optimum basis, while the quantum correlation is characterized as a series of residual correlations in the bases mutually unbiased (MU) to the optimum basis. In this paper, we use the fact that the essential feature of the quantum correlation is that it can be present in any two mutually unbiased bases (MUBs) simultaneously. Thus, one of the two bases is not necessarily the optimum basis to reveal the maximal classical correlation in this paper. With respect to the measure proposed here, we shall show that only the product states do not contain quantum correlation. A product state contains neither any quantum correlation nor any classical correlation; while any non-product bipartite state contains correlation that is fundamentally quantum! We shall also reveal interesting properties of this measure by comparing this measure to other measures of quantum correlation for several families of bipartite states.
The MUBs constitute now a basic ingredient in many applications of quantum information processing: quantum state tomography24, quantum cryptography25, discrete Wigner function26, quantum teleportation27, quantum error correction codes28 and the mean king's problem29. Two orthonormal bases {|ψi〉} and {|ϕj〉} of a d-dimensional Hilbert space H are said to be mutually unbiased if and only if

In a d-dimensional Hilbert space, there exist at least 3 MUBs (when d is a power of a prime number, a full set of d + 1 MUBs exists, more details can be found in Ref. 30).
We recall the quantity defined in Ref. 23. Let Hab = Ha Hb with dim Ha = da and dim Hb = db be the state space of the bipartite system A+B shared by Alice and Bob. Let {|i〉} and |j′〉 be the orthonormal bases of Ha and Hb respectively. Alice selects a basis {|i〉} of Ha and performs a measurement projecting her system onto the basis states. The Holevo quantity χ{ρab|{|i〉}} of ρab with respect to Alice's local projective measurement onto the basis {|i〉〈i|}, is defined as
Hb with dim Ha = da and dim Hb = db be the state space of the bipartite system A+B shared by Alice and Bob. Let {|i〉} and |j′〉 be the orthonormal bases of Ha and Hb respectively. Alice selects a basis {|i〉} of Ha and performs a measurement projecting her system onto the basis states. The Holevo quantity χ{ρab|{|i〉}} of ρab with respect to Alice's local projective measurement onto the basis {|i〉〈i|}, is defined as  . A basis {|i〉} that achieves the maximum (denoted as C1(ρab)) of the Holevo quantity is called a C1-basis of ρab. There could exist many C1-bases for a state ρab and the set of these bases is denoted as
. A basis {|i〉} that achieves the maximum (denoted as C1(ρab)) of the Holevo quantity is called a C1-basis of ρab. There could exist many C1-bases for a state ρab and the set of these bases is denoted as  . Let
. Let  be the set of all bases that are mutually unbiased to Πa,
be the set of all bases that are mutually unbiased to Πa,  . The quantity of quantum correlation in Ref. 23, denoted by Q2(ρab), is defined as
. The quantity of quantum correlation in Ref. 23, denoted by Q2(ρab), is defined as

In other words, Q2 is defined as the Holevo quantity of Bob's accessible information about Alice's results, maximized over Alice's projective measurements in the bases that are mutually unbiased to a C1-basis  and further maximized over all possible C1-bases (if not unique). Thus, Q2 is actually the maximum correlation present simultaneously in any set of two MUBs of which one is a C1-basis.
and further maximized over all possible C1-bases (if not unique). Thus, Q2 is actually the maximum correlation present simultaneously in any set of two MUBs of which one is a C1-basis.
Results
Our approach - Correlation measure based on MUBs
We now present our approach in a more general way.
Definition
Let Δ denote the set of all two-MUB sets, i.e.,

We define

The quantity  represents the maximal amount of correlation that is present simultaneously in any two MUBs. Similar to the other usual measures of quantum correlation,
represents the maximal amount of correlation that is present simultaneously in any two MUBs. Similar to the other usual measures of quantum correlation,  is local unitary invariant, that is,
is local unitary invariant, that is,  for any unitary operators Ua and Ub acting on Ha and Hb respectively.
for any unitary operators Ua and Ub acting on Ha and Hb respectively.
 versus
versus 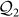
Although both  and Q2 represent quantum correlation (here the symbol
and Q2 represent quantum correlation (here the symbol  is associated with Correlation in two MUBs) instead of classical correlation (represented by C1), they are actually quite different. As
is associated with Correlation in two MUBs) instead of classical correlation (represented by C1), they are actually quite different. As  is defined as the maximum correlation present simultaneously in any two MUBs while Q2 is the maximum correlation present simultaneously in two MUBs of which one is a C1-basis, it is obvious that
is defined as the maximum correlation present simultaneously in any two MUBs while Q2 is the maximum correlation present simultaneously in two MUBs of which one is a C1-basis, it is obvious that

for any ρab. In a sense,  is more essential than Q2 since the maximum in the former one is taken over arbitrarily two MUBs. Thus,
is more essential than Q2 since the maximum in the former one is taken over arbitrarily two MUBs. Thus,  may reveal more quantum correlation than Q2.
may reveal more quantum correlation than Q2.
From the following Theorem and Examples, one knows that there do exist states such that  (Example 4) and
(Example 4) and  (Examples 1,2,3). A clear illustration of the difference between
(Examples 1,2,3). A clear illustration of the difference between  and Q2 is also given in Fig. 3. We know that Q2 does not exceed quantum discord D for all the known examples23. However, one can easily find states such that
and Q2 is also given in Fig. 3. We know that Q2 does not exceed quantum discord D for all the known examples23. However, one can easily find states such that  exceeds quantum discord D (See Fig. 3).
exceeds quantum discord D (See Fig. 3).
Different measures of quantum correlation for two special classes of states:  (left) and
(left) and  (right).
(right).
In each figure, the red curve represents our measure  , the green curve represents the quantum discord D, the blue curve represents the measure Q2 and the dashed orange curve represents the entanglement of formation Ef.
, the green curve represents the quantum discord D, the blue curve represents the measure Q2 and the dashed orange curve represents the entanglement of formation Ef.
The nullity of 
Now we show that any bipartite quantum state contains nonzero correlation simultaneously in two mutually unbiased bases unless it is a product state, this result is stated as the following theorem, while the proof is left to the Method.
Theorem
 if and only if ρab is a product state.
if and only if ρab is a product state.
In a sense, this theorem implies that, any non-product bipartite state contains genuine quantum correlation and  reveals the amount of quantum correlation in the state. In addition, we know that
reveals the amount of quantum correlation in the state. In addition, we know that  is different from the quantity Q2 in Ref. 23 since Q2(ρcq) = 0 for any classical-quantum state ρcq while
is different from the quantity Q2 in Ref. 23 since Q2(ρcq) = 0 for any classical-quantum state ρcq while  only for product states. The difference between the measure
only for product states. The difference between the measure  and other measures of quantum correlation shall be discussed below for several families of bipartite states in more details.
and other measures of quantum correlation shall be discussed below for several families of bipartite states in more details.
Now, we shall calculate the quantity for several families of bipartite states and see how our measure in terms of MUBs is well justified as a measure of quantum correlation.
Example 1 - Pure states
For a bipartite pure state with the Schmidt decomposition  ,
,  . It can be easily checked that
. It can be easily checked that  coincides with the entropy of either reduced state for any pure state, which is also the usual measure of entanglement in a pure state.
coincides with the entropy of either reduced state for any pure state, which is also the usual measure of entanglement in a pure state.
Example 2 - Werner states
Next, we consider the Werner states of a d d dimensional system5,
d dimensional system5,

where −1 ≤ α ≤ 1, I is the identity operator in the d2-dimensional Hilbert space and  is the operator that exchanges A and B. For a local measurement with respect to basis states {|ei〉} of Ha, with probability
is the operator that exchanges A and B. For a local measurement with respect to basis states {|ei〉} of Ha, with probability  , Alice will obtain the k-th basis state |ek〉 and Bob will be left with the state
, Alice will obtain the k-th basis state |ek〉 and Bob will be left with the state  , where
, where  with αkj = 〈ek|j〉. It is straightforward to show that
with αkj = 〈ek|j〉. It is straightforward to show that

The entanglement of formation Ef for the Werner states is given as  , with h(x) ≡ −x log2x − (1 − x) log2(1 − x)31. The three different measures of quantum correlation, i.e.,
, with h(x) ≡ −x log2x − (1 − x) log2(1 − x)31. The three different measures of quantum correlation, i.e.,  , the quantum discord D and the entanglement of formation Ef, are illustrated in Fig. 1 for comparison. From this figure, we see that the curve for entanglement of formation intersects the other two curves; thus, Ef can be larger or smaller than
, the quantum discord D and the entanglement of formation Ef, are illustrated in Fig. 1 for comparison. From this figure, we see that the curve for entanglement of formation intersects the other two curves; thus, Ef can be larger or smaller than  .
.
Example 3 - Isotropic states
For the d d isotropic states
d isotropic states

where P+ = |Φ+〉 〈Φ+|,  is the maximally entangled pure state in
is the maximally entangled pure state in  . Let {|ek〉 〈ek|} be an arbitrarily given projective measurement on Alice's part. Bob's state after after Alice gets the k-th measurement result is
. Let {|ek〉 〈ek|} be an arbitrarily given projective measurement on Alice's part. Bob's state after after Alice gets the k-th measurement result is

where  with αkj = 〈ek|j〉. As the eigenvalues of
with αkj = 〈ek|j〉. As the eigenvalues of  does not depend on the basis for Alice's measurement, one can easily show that
does not depend on the basis for Alice's measurement, one can easily show that

The entanglement of formation Ef for the isotropic states is given as32,33

where  . The quantum discord of the isotropic state is34
. The quantum discord of the isotropic state is34

The three different measures of quantum correlation, i.e.,  , the quantum discord D and the entanglement of formation Ef, are illustrated in Fig. 2 for comparison. From this figure, we see that the curve for entanglement of formation intersects the other two curves; thus, Ef can be larger or smaller than
, the quantum discord D and the entanglement of formation Ef, are illustrated in Fig. 2 for comparison. From this figure, we see that the curve for entanglement of formation intersects the other two curves; thus, Ef can be larger or smaller than  .
.
Example 4 - A family of two-qubit states
As the last example, we consider a family of two-qubit states that are Bell-diagonal states. This family of states admit the form

We rearrange the three numbers {r1, r2, r3} according to their absolute values and denote the rearranged set as { ,
,  ,
,  } such that
} such that  . Next we show that
. Next we show that

Without loss of generality, we prove (14) only for the case  . A projective measurement performed on qubit A can be written as
. A projective measurement performed on qubit A can be written as  , parameterized by the unit vector
, parameterized by the unit vector  . When Alice obtains p±, Bob will be in the corresponding states
. When Alice obtains p±, Bob will be in the corresponding states  , each occurring with probability
, each occurring with probability  . The entropy
. The entropy  reaches its minimum value
reaches its minimum value  when
when  . Let
. Let  and
and  with ax + by = 0, then
with ax + by = 0, then  is mutually unbiased to
is mutually unbiased to  , where
, where  ,
,  . It is immediate that
. It is immediate that  and
and  . Thus
. Thus  as desired since h(c) is a monotonic decreasing function when
as desired since h(c) is a monotonic decreasing function when  . Our quantity
. Our quantity  is compared with the quantum discord D and the entanglement of formation Ef for ρ1 and ρ2 in Fig. 3.
is compared with the quantum discord D and the entanglement of formation Ef for ρ1 and ρ2 in Fig. 3.
From the left figure of Fig. 3, it is clear that  is quite different from both D and Q2. Unlike Q2 that does not exceed D for all known examples,
is quite different from both D and Q2. Unlike Q2 that does not exceed D for all known examples,  can exceed D. We have
can exceed D. We have  when p is closed to
when p is closed to  , while
, while  when p is closed to 0 or 1; we also have
when p is closed to 0 or 1; we also have  when
when  and
and  increases monotonously while Q2(ρ1) decreases monotonously when p deviates from
increases monotonously while Q2(ρ1) decreases monotonously when p deviates from  . In Fig. 3, the difference between our measure
. In Fig. 3, the difference between our measure  and the other measures is well illustrated by the extreme cases when p = 0 or 1 in the left figure and when p = 0 in the right figure. For example, for
and the other measures is well illustrated by the extreme cases when p = 0 or 1 in the left figure and when p = 0 in the right figure. For example, for  , our measure has a finite value while the other measures vanish.
, our measure has a finite value while the other measures vanish.
Correlation revealed via more MUBs
In addition, we can define a quantity based on m MUBs (3 ≤ m ≤ dim Ha + 1), namely,

where

It is clear that  . The following are obvious from the arguments in the previous examples: i)
. The following are obvious from the arguments in the previous examples: i)  if and only if ρ is a product state, ii)
if and only if ρ is a product state, ii)  for both the Werner states and the isotropic states and iii)
for both the Werner states and the isotropic states and iii)  for the family of two-qubit states in Eq. (13).
for the family of two-qubit states in Eq. (13).
Discussion
We have provided a very different approach to quantify quantum correlation in a bipartite quantum state. Our approach captures the essential feature of quantum correlation: the simultaneous existence of correlations in complementary bases. We have proved that the only states that don't have this feature are the product states, which contains no correlation (classical or quantum) at all. Thus, any non-product state contains correlation that is fundamentally quantum. This feature of quantum correlation characterized here could be the key feature that enables quantum key distribution (QKD) with entangled states, since the quantum correlation that exists simultaneously in MUBs, which can be quantified by  , is the resource for entanglement-based QKD via MUBs.
, is the resource for entanglement-based QKD via MUBs.
Method
Proof of the Theorem in the Main Text
The ‘if’ part is obvious and we only need to show the ‘only if’ part. In other words, we only need to prove that ρab = ρa ρb if either
ρb if either  or
or  for any MUB pair
for any MUB pair  . It is equivalent to show that both
. It is equivalent to show that both  and
and  for a certain MUB pair
for a certain MUB pair  if ρab is not a product state.
if ρab is not a product state.
We assume that ρab is not a product state, then the maximal classical correlation is nonzero, i.e., C1(ρab) ≠ 0. Let  , we have χ(ρab|{|ei〉}) ≠ 0. Therefore, we only need to find a second basis (MU to {|ei〉}) such that the corresponding Holevo quantity is nonzero. We denote the projective measurement corresponding to {|ei〉} by
, we have χ(ρab|{|ei〉}) ≠ 0. Therefore, we only need to find a second basis (MU to {|ei〉}) such that the corresponding Holevo quantity is nonzero. We denote the projective measurement corresponding to {|ei〉} by  . Then
. Then  . As C1(ρab) ≠ 0, we know that
. As C1(ρab) ≠ 0, we know that  and
and  at least for some k0 and l0. We arbitrarily choose a basis {|fi〉} that is MU to {|ei〉}. If χ{ρab|{|fi〉}} ≠ 0, then we already obtain the second basis and the theorem is true.
at least for some k0 and l0. We arbitrarily choose a basis {|fi〉} that is MU to {|ei〉}. If χ{ρab|{|fi〉}} ≠ 0, then we already obtain the second basis and the theorem is true.
If χ{ρab|{|fi〉}} = 0, we can construct the MUB pair as follows. As in this case, the measurement corresponding to {|fi〉} yields the following output state

Thus, ρab can be represented as

with respect to the local basis {|fi〉} and at least one of the off-diagonal blocks is not zero (otherwise, ρab is a product state). Without loss of generality we assume that the (1,2)-block-entry of the above matrix is nonzero. It follows that there exists a 2 by 2 unitary matrix U2, such that, under the local basis {U2 ⊕ Id−2|fi〉}, the state admits the form

with  and σb ≠ ρb. That is χ{ρab|{U2 ⊕ Id−2|fi〉}} ≠ 0. This unitary matrix U2 can be chosen as
and σb ≠ ρb. That is χ{ρab|{U2 ⊕ Id−2|fi〉}} ≠ 0. This unitary matrix U2 can be chosen as

with  a very small positive number. Even though χ{ρab|{U2 ⊕ Id−2|fi〉}} could be very small, it is nonzero. As
a very small positive number. Even though χ{ρab|{U2 ⊕ Id−2|fi〉}} could be very small, it is nonzero. As  is a very small and χ{ρab|{|ei〉}} ≠ 0, we also have χ{ρab|{U2 ⊕ Id−2|ei〉}} ≠ 0. Thus, the Holevo quantity is nonzero at least for a certain MUB pair (i.e., {U2 ⊕ Id−2|ei〉} and {U2 ⊕ Id−2|fi〉}) and therefore
is a very small and χ{ρab|{|ei〉}} ≠ 0, we also have χ{ρab|{U2 ⊕ Id−2|ei〉}} ≠ 0. Thus, the Holevo quantity is nonzero at least for a certain MUB pair (i.e., {U2 ⊕ Id−2|ei〉} and {U2 ⊕ Id−2|fi〉}) and therefore  .
.
Thus,  for any ρab that is not a product state. The proof is completed.
for any ρab that is not a product state. The proof is completed.
References
Einstein, A., Podolsky, B. & Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780 (1935).
Schrödinger, E. Die gegenwärtige Situation in der Quantenmechanik. Naturwissenschaften 23, 807–812 (1935).
Einstein, A., Born, M. & Born, H. The Born-Einstein Letters: correspondence between Albert Einstein and Max and Hedwig Born from 1916 to 1955 (Walker, New York, 1971).
Bennett, C. H., Bernstein, H. J., Popescu, S. & Schumacher, B. Concentrating partial entanglement by local operations. Phys. Rev. A 53, 2046–2052 (1996).
Werner, R. F. Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model. Phys. Rev. A 40, 4277–4281 (1989).
Horodecki, R., Horodecki, P., Horodecki, M. & Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 81, 65–942 (2009).
Gühne, O. & Tóth, G. Entanglement detection. Phys. Rep. 474, 1 (2009).
Usha Devi, A. R. & Rajagopal, A. K. Generalized Information Theoretic Measure to Discern the Quantumness of Correlations. Phys. Rev. Lett. 100, 140502 (2008).
Eltschka, C. & Siewert, J. Negativity as an Estimator of Entanglement Dimension. Phys. Rev. Lett. 111, 100503 (2013).
Oppenheim, J., Horodecki, M., Horodecki, P. & Horodecki, R. Thermodynamical Approach to Quantifying Quantum Correlations. Phys. Rev. Lett. 89, 180402 (2002).
Skrzypczyk, P., Navascués, M. & Cavalcanti, D. Quantifying Einstein-Podolsky-Rosen Steering. Phys. Rev. Lett. 112, 180404 (2014).
Vedral, V. Quantum entanglement. Nature Phys. 10, 256 (2014).
Georgescu, I. Quantum entanglement: Now you see it. Nature Phys. 9, 394 (2013).
Strobel, H. et al. Fisher information and entanglement of non-Gaussian spin states. Science 345, 424 (2014).
Yu, T. & Eberly, J. H. Sudden Death of Entanglement. Science 323, 598 (2009).
Dakić, B. et al. (2012) Quantum discord as resource for remote state preparation.Nature Phys. 8, 666.
Wu, S., Poulsen, U. V. & Mølmer, K. Correlations in local measurements on a quantum state and complementarity as an explanation of nonclassicality. Phys. Rev. A 80, 032319 (2009).
Luo, S. Using measurement-induced disturbance to characterize correlations as classical or quantum. Phys. Rev. A 77, 022301 (2008).
Modi, K., Brodutch, A., Cable, H., Paterek, T. & Vedral, V. The classical-quantum boundary for correlations: Discord and related measures. Rev. Mod. Phys. 84, 1655 (2012).
Ollivier, H. & Zurek, W. H. Quantum Discord: A Measure of the Quantumness of Correlations. Phys. Rev. Lett. 88, 017901 (2001).
Luo, S. & Fu, S. Measurment-induced nonlocality. Phys. Rev. Lett. 106, 120401 (2011).
Bell, J. S. On the Einstein Podolsky Rosen paradox. Physics 1, 195–200 (1964).
Wu, S., Ma, Z., Chen, Z. & Yu, S. Reveal quantum correlation in complementary bases. Sci. Rep. 4, 4036 (2014).
Wootters, W. K. & Fields, B. D. Optimal state-determination by mutually unbiased measurements. Ann. Phys. (N.Y.) 191, 363 (1989).
Bechmann-Pasquinucci, H. & Peres, A. Quantum cryptography with 3-state systems. Phys. Rev. Lett. 85, 3313 (2000).
Wootters, W. K. A Wigner-function formulation of finite-state quantum mechanics. Ann. Phys. (N.Y.) 176, 1 (1987).
Koniorczyk, M., Buzek, V. & Janszky, J. Wigner-function description of quantum teleportation in arbitrary dimensions and a continuous limit. Phys. Rev. A 64, 034301 (2001).
Paz, J. P., Roncaglia, A. J. & Saraceno, M. Qubits in phase space: Wigner-function approach to quantum-error correction and the mean-king problem. Phys. Rev. A 72, 012309 (2005).
Englert, B. G. & Aharonov, Y. The mean king's problem: prime degrees of freedom. Phys. Lett. A 284, 1 (2001).
Durt, T., Englert, B. G., Bengtsson, I. & Zyczkowski, K. On mutually unbiased bases. Int. J. Quant. Inf. 8, 535 (2010).
Wootters, W. K. Entanglement of formation and concurrence. Quant. Inf. & Comp. 1, 27–34 (2001).
Terhal, B. M. & Vollbrecht, K. G. H. Entanglement of Formation for Isotropic States. Phys. Rev. Lett. 85, 2625 (2000).
Fei, S. M. & Li-Jost, X. R function related to entanglement of formation. Phys. Rev. A 73, 024302 (2006).
Chitambar, E. Quantum correlation in high-dimensional states of high symmetry. Phys. Rev. A 86, 032110 (2012).
Acknowledgements
Y. Guo acknowledges support from the Natural Science Foundation of China (No. 11301312, No. 11171249), the Natural Science Foundation of Shanxi (No. 2013021001-1, No. 2012011001-2) and the Research start-up fund for Doctors of Shanxi Datong University (No. 2011-B-01). S. Wu acknowledges support from the Natural Science Foundation of China (No. 11275181) and the Fundamental Research Funds for the Central Universities (No. 20620140007).
Author information
Authors and Affiliations
Contributions
Y.G. and S.W. contributed equally to the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Guo, Y., Wu, S. Quantum correlation exists in any non-product state. Sci Rep 4, 7179 (2014). https://doi.org/10.1038/srep07179
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07179
This article is cited by
-
One-way deficit and Holevo quantity of generalized n-qubit Werner state
Quantum Information Processing (2023)
-
A Note on Holevo Quantity of SU(2)-invariant States
International Journal of Theoretical Physics (2022)
-
Any entanglement of assistance is polygamous
Quantum Information Processing (2018)
-
Measurement-based quantum correlation in mixed-state quantum metrology
Quantum Information Processing (2018)
-
Non-commutativity measure of quantum discord
Scientific Reports (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.




 versus
versus 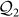

 , the green curve represents the quantum discord D and the blue curve represents the entanglement of formation Ef.
, the green curve represents the quantum discord D and the blue curve represents the entanglement of formation Ef.
 , the blue curve represents the quantum discord D and the green curve represents the entanglement of formation Ef.
, the blue curve represents the quantum discord D and the green curve represents the entanglement of formation Ef.
