Abstract
Light carrying an orbital angular momentum (OAM) displays an optical phase front rotating in space and time and a vanishing intensity, a so-called vortex, in the center. Beyond continuous-wave vortex beams, optical pulses with a finite OAM are important for many areas of science and technology, ranging from the selective manipulation and excitation of matter to telecommunications. Generation of vortex pulses with a duration of few optical cycles requires new methods for characterising their coherence properties in space and time. Here we report a novel approach for flexibly shaping and characterising few-cycle vortex pulses of tunable topological charge with two sequentially arranged spatial light modulators. The reconfigurable optical arrangement combines interferometry, wavefront sensing, time-of-flight and nonlinear correlation techniques in a very compact setup, providing complete spatio-temporal coherence maps at minimum pulse distortions. Sub-7 fs pulses carrying different optical angular momenta are generated in single and multichannel geometries and characterised in comparison to zero-order Laguerre-Gaussian beams. To the best of our knowledge, this represents the shortest pulse durations reported for direct vortex shaping and detection with spatial light modulators. This access to space-time coupling effects with sub-femtosecond time resolution opens new prospects for tailored twisted light transients of extremely short duration.
Similar content being viewed by others
Introduction
The generation of light with well-defined spatial and temporal coherence properties represents one of the central topics of modern optics with high relevance for basic studies of light-matter interaction and a broad range of applications in optical technologies. While steady-state, i.e., continuous-wave optical beams have been generated with a substantial variety of spatially constant phase fronts, work on light with a phase front rotating in space and time has remained limited. Such beams carry an external orbital angular momentum (OAM) in addition to the internal momentum or spin of the photons. Recently, ultrashort optical pulses which consist of few cycles of the optical carrier wave and display a well-defined OAM, have received strong interest as a tool for exploring nonlinear light-matter interactions in a new transient regime1,2,3.
In a classical picture, the OAM is explained by a twist of the wavefront as the result of multiple coupled rotations (inset of Fig. 1). The number of intertwined rotations is usually described by a parameter referred to as topological charge4. It has been shown that the shape stability of vortex Bessel beams during the propagation in turbulent atmosphere enhances with higher order topological charges5. Moreover, the transfer of OAM to matter was applied to mechanically rotate particles in optical tweezers6 and to induce mass transport phenomena on surfaces7 or with molecules8. For next generation optical communication, the topological charge promises, in combination with entanglement, to yield a degree of freedom for high-capacity information encoding9,10 in addition to the classical channels for data transfer such as spectrum, polarisation, intensity and time. Here, the parallel generation and processing of many vortex beams represents a particular challenge. The potential of vortex beams for superresolution microscopy is currently investigated as well11.
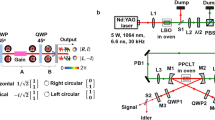
Experimental setup for temporal coherence mapping of few-cycle vortex pulses with two subsequently arranged spatial light modulators.
Ultrashort pulses from a Ti:sapphire laser (6.5 fs, 800 nm, 80 MHz) are reflected from a first spatial light modulator (SLM1, generation part) to shape a pulsed vortex beam (Inset: schematic of a twisted pulse). This beam is coupled into a Michelson interferometer containing a beam splitter (BS) and producing phase-locked pulse pairs with variable delay (mirrors M1, M2). Wavefront and local temporal coherence are analysed by a nonlinear Shack-Hartmann sensor consisting of axicons programmed in a second spatial light modulator (SLM2, characterisation part), a 10-μm thick nonlinear crystal (BBO) for second harmonic generation, a filter to suppress the fundamental light and a matrix camera detector (EMCCD). By modifying this modular setup, two geometrical configurations with (a) single vortex beams and (b) multiple vortex beams were studied. Dispersion is compensated by 4 double chirped mirrors (DCMs) and a pair of thin CaF2 wedges. For reasons of simplicity, only one DCM mirror is shown in the figure.
A quantitative characterisation of spatial and temporal coherence is mandatory for a reliable application of light fields carrying an OAM. Recently, a combination of Shack-Hartmann (S-H) wavefront sensor and Michelson interferometer was applied for reconstructing the coherence properties of partially coherent vortex beams12. While this work addresses the spatial aspects of coherence, ultrashort vortex pulses require a detailed temporal characterisation as well. At pulse durations corresponding to a few optical cycles, the interplay of travel time, angular profile, spectrum and nonlinearities leads to specific space-time coupling13 and spatio-temporal localisation effects. For an analysis of spatial and temporal coherence, S-H-sensors have been combined with nonlinear autocorrelation14 or frequency resolved optical gating (FROG) methods15,16,17. Another promising approach is the interferometric field reconstruction in combination with a time-slicing technique18. This method has been applied to characterise intense single-beam vortex pulses of >50 μJ pulse energy generated by optical parametric amplification19. Spectrally-resolved interferograms and intensity profiles have been used to evaluate the dispersion and to determine the pulse duration.
In this article, we report the generation and analysis of sub-3-cycle vortex pulses with a novel compact and versatile double-stage optical arrangement which integrates two spatial light modulators (SLMs). In this new scheme, the SLMs are operated in a generation part and a characterisation part. The wavefront structure and the spatially resolved temporal coherence of sub-7-fs vortex pulses of different topological charges are analysed simultaneously. The specific advantages of the technique are demonstrated by flexible and adaptive shaping and recognition of multichannel vortex pulses of variable topological charge.
Results and Discussion
The experimental setup is shown in Fig. 1. The ultrashort wavepackets to be characterised were generated by a Ti:sapphire laser oscillator emitting 6.5-fs broadband pulses with pulse energies in the few-nanojoule range at a central wavelength of about 800 nm. Our novel, highly compact setup includes two independent, phase-only, low-dispersion spatial light modulators working in reflection. In contrast to previous experiments on direct vortex generation and characterization of significantly longer pulses (200-fs range) with a single phase-only SLM20, the requirements to the transfer characteristics and the design of the complete optical setup are much more challenging here. The first SLM (SLM1) in the setup acts as a vortex beam shaper by mimicking a variable spiral phase plate and imprints a well-defined OAM on the optical pulses (generation part of the setup). A second SLM (SLM2) is operated as a programmable axicon array which represents the central part of a reconfigurable nondiffracting S-H wavefront sensor21 (characterisation part of the setup). The needle-shaped sub-beams, i.e., the central lobes of Bessel beams22,23,24 propagate with low diffraction and low dispersion over relatively long distances so that different parts of the wavefront stay separated and the temporal coherence information remains essentially propagation invariant within these nondiffracting zones23. The aberrations (in particular the beam ellipticity at large incident angles) are corrected by a transformation of the phase axicons21.
The combination of the S-H sensor with a balanced Michelson interferometer, second harmonic generation (SHG) in a thin BBO crystal and the EMCCD camera provides a multichannel nonlinear autocorrelation of the pulses in addition to the wavefront analysis. Both wavefront and temporal coherence maps of the wavepackets of interest are extracted from the combined measurement and yield a spatially discretised picture of the angular-temporal pulse characteristics. The SLMs were carefully selected after characterising their suitability with respect to temporal transfer, linear phase response on the programmed grey levels and pixel geometry. Both the wavefront division in the characterisation part and the complex beam structuring in the shaping part require a high pixel resolution and a large fill factor. The dispersion of the complete optical arrangement was compensated by 4 double chirped mirrors (DCMs) and a pair of thin CaF2 wedges.
The building blocks of the setup can easily be rearranged to either work in autocorrelation or in wavefront mode only, i.e., to either perform reference measurements or to apply the well-defined wavepackets to further applications. To demonstrate the specific flexibility of the arrangement, two different types of geometrical configurations with shaping (a) a single vortex beam (single-channel geometry) and (b) a 2 × 2 array of vortex beams (multichannel geometry) with stepwise-varying topological charges are demonstrated in the following.
In a first set of experiments, single-beam vortex pulses were studied. Fig. 2 shows the spatial structures of Gaussian and Laguerre-Gaussian vortex beams of different topological charges after frequency conversion to the second harmonic and time-integrated detection with the EMCCD camera. To obtain the SHG images without wavefront division, SLM2 had to be switched out. The frequency conversion leads to a quadratic enhancement of the intensity contrast compared to the beam at the fundamental frequency. In Fig. 3(a) and 3(b), the angular distributions of the fundamental and SHG of a vortex beam with a topological charge m = 1 at the fundamental wavelength are compared with each other by the Shack-Hartmann wavefront sensing method. The wavefront twist is indicated by the rotation of the displacement vectors (arrows). The spatio-temporal characteristics clearly reveal the vortex nature of the wavepackets with an OAM corresponding to topological charges of m = 1 in Fig. 3(a) and mSHG = 2 in Fig. 3(b), the latter resulting from the frequency-doubling25,26.
Time integrated SHG signal of few-cycle Gaussian and Laguerre-Gaussian beams.
The examples show the adaptive shaping of vortex beams of different topological charges (m = 0 to 3) in the fundamental with low-dispersion LCoS-SMSs. The frequency conversion doubles the topological charge (mSHG = 0 to 6). Scratch-like substructures in the profiles are caused by inhomogeneities in the SHG crystal.
Wavefront twist of few-cycle vortex pulses measured in the Shack-Hartmann configuration.
The sub-beams are generated by programming axicons in SLM2 (setup in Fig. 1). Orbital angular momenta are indicated by maps of transversal Poynting vector components for (a) fundamental and (b) SHG wavelengths (normalised, after analysing the intensity spot displacements of a reconfigurable nondiffracting S-H wavefront sensor). The respective topological charges are m = 1 and mSHG = 2. The different lengths of the vectors in (a) and (b) are directly proportional to these numbers.
The vectorial structure of the vortices and topological charge are directly indicated by Shack-Hartmann wavefront sensing26,27. The angular resolution Δθ is mainly determined by the distance between SLM and BBO crystal and the camera pixel dimensions. For an axial distance of 70 mm, a value of Δθ < 0.2 mrad is estimated.
Fig. 4 shows the spatially resolved temporal autocorrelation traces of two different ultrashort-pulsed beams, one with a Gaussian profile (m = 0) and a second one with a Laguerre-Gauss profile (mSHG = 2). While the complete coherence data set is three-dimensional (two spatial and one temporal coordinate), we plot the second harmonic signal derived from central cuts through the spot arrays as a function of the spatial coordinate x and the time delay between the two pulse replica generated in the interferometer. The temporal coherence information is given by the contrast of the second order autocorrelation function. The autocorrelation plots in Fig. 4 reveal the curvature of the field oscillations in the space-time frame. The relative delay between the arrival times at different spatial coordinates yields information on the wavefront curvature or - by comparing with a reference wave - any low-dispersion phase object in the optical path. It is important to note that the arrival time analysis on a few-femtosecond time scale corresponds to a spatial length range which is some 3 orders of magnitude smaller than the length range covered by the transversal deflection of sub-beams on a few-millimeter scale as analysed in a S-H sensor. Thus, a combined time-wavefront sensor detects wavefront features on both scales simultaneously but with different resolution.
Spatially resolved temporal coherence of few-cycle pulses without and with orbital angular monentum.
Spatially resolved temporal coherence maps obtained by second-order autocorrelation of a Gaussian and a Laguerre-Gauss beam with topological charges of (a) mSHG = 0 and (b) mSHG = 2. The distributions were derived from central cuts through the spot arrays (data corresponding to Fig. 3b). The data sets allow for a reconstruction of complete 3D temporal coherence profiles. The conservation of temporal coherence information along the selected cut direction is indicated by homogeneous spatio-temporal distributions of the pulse duration in both cases. The detailed analysis shows some slight inhomogeneities over the beam cross section (cf. Figs. 6a, b). The curvature in time indicates the wavefront curvature of the field cycles in space. The theoretical time resolution is about 0.12 fs. Insets: cut profiles along the red bows and corresponding envelope (green solid curve). The centre-to-centre distance between neighbouring sub-beams of the orthogonal beam array was about 478 μm in this experiment.
The temporal pulse properties were studied with spatial resolution (Fig. 5). To visualise the temporal wavefront (pulse front), the (averaged) three-dimensional shape of a single selected field cycle (maximum) is filtered out of the extended data set and plotted in Fig. 5(a). The temporal wavefront tilt over a beam area of approximately 6 × 6 mm2 is less than 300 as, corresponding to a length scale of the order of 100 nm or λ/8 where λ ≈ 800 nm is the center wavelength of the ultrashort pulses. The wavefront of this subcycle has an average radius of curvature of about 9.17 m. The measurements show that, in contrast to conventional autocorrelators or other single-channel pulse characterisation systems, the multichannel architecture of the Shack-Hartmann setup with nondiffracting sub-beams enables not only to work nearly independent of specific errors in time domain caused by the wavefront curvature but also to reconstruct angular profiles from time-of-flight information.
Temporal wavefront and coherence maps.
(a) Wavefront curvature of a selected field cycle. The curved surface was interpolated from the centers of gravity of the measured local second order temporal autocorrelation functions within the line of highest field strength (from the 3D autocorrelation data set used in Fig. 3). It represents the spatial pulse front of a particular subcycle. (b), (c) Temporal coherence maps of few-cycle Gaussian (bottom, left) and Laguerre-Gaussian beams (bottom, right) were determined by autocorrelation measurements. The columns show distribution of the FWHM of the second order autocorrelation functions for temporal cuts along the propagation axes of all sub-beams (needle beams). The uncertainty of the FWHM of the local autocorrelation functions is less than ±400 attoseconds. Opposite angles of view were chosen for the two plots to better visualise the relevant features.
Figures 5(b) and (c) show the complex coherence map of the electrical field oscillations for a Gaussian and a Laguerre-Gaussian wavepacket, respectively. To suppress high frequency distortions, the temporal coherence data were retrieved from the power spectrum of the Fourier transform of all local autocorrelation traces after low pass filtering28. The minimum, maximum and averaged pulse duration as derived from the width of the autocorrelation functions in Fig. 5(b) was 6.6 fs, 7.5 fs and 7.1 fs, respectively. The standard deviation for the N = 80 analysed spatial channels was below ±0.4 fs.
From the spatial profile of the second order temporal autocorrelation in Fig. 5(c) which approximately resembles a vortex structure, the maximum difference of the corresponding quadratic dispersion is estimated to be about 3.8 fs2. This value is accounted for by the pulse transfer through the liquid layer of the shaping LCoS-SLM and potential contributions by spatio-spectral interference.
The space-time structure of a selected sub-3-cycle sub-beam (needle beam) of the S-H sensor without and with dispersion compensation is shown in Fig. 6. The average difference in the derived pulse duration is 7%, corresponding to a path difference of 135 nm (average phase difference of about 0.34 π). The measured pulse lengthening without correction is in the range of 0.45 fs (for an initial FWHM pulse duration of about 6.4 fs). The spatial resolution of our setup is limited by the pitch and size of the camera pixels and by the quality of the imaging system. The temporal resolution results from the accuracy of the interferometer steps, vibrations and air turbulences. The minimum applied step width of the piezo-actuator of 20 nm corresponds to a phase step of 40 nm (double pass in the interferometer) and a time resolution of about 0.133 fs in air under undistorted conditions. It should be noted that a spectrally resolved detection of the second harmonic signal allows for determining the optical phase of the pulses via frequency-resolved optical gating (FROG).
Correction for spatio-temporal aberrations.
(a) The spatially resolved second order autocorrelation function of one of the nondiffracting sub-beams (“needle beams”) of the Shack-Hartmann sensor under strong off-axis conditions (angle of incidence about 43°) reveals significant spatio-temporal coupling effects corrupting the pulse quality. The resulting pulse duration was by about 450 attoseconds longer compared to the corrected case (10 fs FWHM of the autocorrelation function, with dispersion compensation) shown in (b). Here, the programmed axicon shape was adapted to the off-axis geometry. For noise reduction and compensation of slight intensity fluctuations at certain time intervals, the experimental data was low-pass filtered.
The programmable ultraflat axicons used for the S-H wavefront analysis provide a high angular resolution as required for resolving even higher order topological charges. In contrast to previous studies with single static shapers29, the use of a second SLM for topological charge encoding opens the possibility to switch as well as to realize multichannel transfer. Because of the well-known self-reconstruction properties of the nondiffracting beams30,31, a high robustness against tilt, displacement and spatio-temporal distortions is a further important advantage of the configuration.
The specific advantages of the concept presented here arise from the combination of the adaptivity of spatial light modulation with the unique properties of nondiffracting needle beams used as the sub-beams of the S-H sensor. This enables to read out even extremely small variations of encoded temporal coherence information (including relative phase delays) with the time resolution of a phase shifting interferometer, i.e., down to the sub-femtosecond time scale.
To demonstrate the potential and flexibility of the tandem approach, we now present a multichannel approach with independently generated and processed vortex beams. The use of an SLM allows for generating transient vortex patterns that change with the SLM modulation rate, a feature highly interesting for information processing. In the experiments, 2 × 2 spiral phase elements were programmed into the phase map of SLM1 (Fig. 7). In the characterisation part, SLM2 was operated as an array of 40 × 40 phase axicons with a maximum phase of π. For analysing the spot displacement maps of all 4 vortices in Shack-Hartmann wavefront sensor mode (Fig. 8a), about 300 needle beams were found to be a sufficient number.
Multichannel vortex generation.
The grey value map was transferred into a phase map of SLM1 for the generation of a 2 × 2 array of thin spiral phase plates (circular areas) with a period of 260 pixels (2.1 mm). To reduce the background signal in the plane of interest, a checkered pattern (2 × 2 pixels per square) was applied to the passive areas between the phase plates (inset). The dark and bright part corresponds to a higher and lower effective refractive index, respectively.
Multichannel vortex detection.
(a) Shack-Hartmann plot. To characterise the vortex beams, SLM2 was operated as Shack-Hartmann wavefront sensor dividing the wavefront by an array of 40 × 40 phase axicons with a maximum phase of π. The magnitudes of the vectors indicate topological charges (1–4, from minimum to maximum length). (b) Data points and from the results shown in (a) in comparison to the theory (red and green curves) for topological charges of m = 1 (blue circles) and 2 (blue squares), respectively. Vectors of the same radii were averaged and the resulting standard deviations were plotted as error bars.
The orientation of the vectors indicates the direction of twist which is identical for all vortices. The magnitudes of the vectors yield the information on the topological charges between 1 and 4 (from minimum to maximum length). In Fig. 8(b), the skew angle β derived from the data (blue symbols) is plotted as a function of the beam radius and compared to theoretical curves (red and green curves) following the formula β = m/kr, where k and r are defined as the wave vector and radius, respectively. The agreement with the experimental and the theoretical results is good with statistical fluctuations of the wavefront of less than 0.4 mrad. Such fluctuations originate from phase distortions in the illuminating beam and in the cover glasses of the SLMs. The reliability to read out the corresponding order of orbital angular momentum was further improved by averaging correlated data (belonging to the same radii). For topological charges from 1 to 4, the identification worked faultlessly.
Conclusions
In conclusion, the combination of nonlinear autocorrelation and reconfigurable nondiffracting Shack-Hartmann techniques represents a powerful approach for analysing the spatial maps of temporal coherence of complex few-cycle vortex beams. Implementing a tandem arrangement of low-dispersion spatial light modulators for shaping and detection, a highly compact and versatile setup is demonstrated which significantly extends the variability of the previous approaches. The flexible generation of “needle beams” with spatially and temporally undistorted propagation along extended focal zones paves the way towards a complete characterisation of ultrashort wavepackets carrying an orbital angular momentum. An adaptive tailoring of single and multiple intense few-cycle vortex pulses offers favourable prospects for many practical applications.
The strongly confined compensation of the temporal dispersion allows for generating nearly perfect ultra-broadband and Fourier-limited pulses in the zone of interest. In contrast to vortex generators based on a reflective continuous-surface MEMS the pixellated SLM structure are much more flexible with respect to the controlled change of beam shape, size and configuration at the SLM frame rates. By blocking or exchanging the functionality of the shaping and characterization parts, a modular operation is enabled. With the very high time resolution demonstrated here, changes of the time-space structure of wavepackets are revealed even down to the sub-femtosecond scale as we demonstrated for few-cycle pulsed Gaussian as well as Laguerre-Gaussian vortex beams. Thanks to the adaptive correction of aberrations, the travel time profile of such pulses was recorded and, for the first time, the fine structure of the spatio-temporal coherence was visualised by the spiral-like profile of the pulse duration in space. The capability for manipulating and detecting vortex pulses in multiple channels was successfully demonstrated with up to 4 independent few-cycle beams of different topological charges.
The available flexibility, precision and sensitivity of the advanced setup are the key to a deeper understanding of ultrashort-pulsed vortex beams, e.g. for the study of the spatio-temporal propagation of aberration-induced perturbations or an analysis of spectral anomalies close to the singularity. We expect that our novel approach will also stimulate new quantum information experiments on high-dimensional state vectors and ultrafast quantum interference, spectral phase retrieval or carrier-envelope phase control.
Methods
Adaptive shaping and diagnostic of few-cycle vortex pulses with an extended Shack-Hartmann sensor
Wavefront forming as well as spatio-temporal coherence mapping are performed in a very compact setup consisting of a tandem arrangement of two phase-only reflective liquid-crystal-on-silicon spatial light modulators (LCoS-SLMs, HoloEye). Broadband 800 nm pulses of about 6.5 fs duration corresponding to approximately 3 cycles of the optical field are generated in a mode-locked Ti:sapphire oscillator (Venteon). The pulses are shaped into a vortex beam of variable topological charge by the first SLM (SLM1, shaping part). Phase-locked pairs of vortex pulses of variable time delay are generated in a Michelson interferometer. The second SLM (SLM2, characterization part) is operated as a programmable axicon array and part of a nondiffracting S-H wavefront sensor21. Compared to low-dispersion MEMS approaches32 which are still less flexible with respect to a free pragramming of functionality, the SLMs require a more careful management of the spectral phase (chirp). The dispersion of the complete optical arrangement was compensated by 4 double chirped mirrors (DCMs) and a pair of thin CaF2 wedges. The double-SLM structure can be modified by either switching the parts on and off or reverse their arrangement. The angle of incidence on SLM1 was chosen to be smaller than 10°. In this near-paraxial case, the spiral phase structure is not essentially affected by the double-pass of the beam through the thin (μm-range) liquid layers and cover glass. Aberrations induced by larger angles, e.g. by beam ellipticity, can be compensated for both SLMs individually. The interferometer part can be easily bypassed by additional mirrors and thus allows specific experiments exploiting the advantages of ultrashort pulsed needle beams with or without OAM properties.
A 10 μm thick BBO crystal serves for second harmonic generation in order to measure the multichannel, i.e., discretely spatially resolved temporal autocorrelation of the pulses in parallel to the spatial wavefront analysis. The resulting interference signals are detected by a highly sensitive electron multiplying charge-coupled device (EMCCD, Andor) with near single photon capability and high dynamic range. This enables to detect the relatively weak second order autocorrelation signals from few-nanojoule pulses even after transforming the fundamental into an array and frequency conversion of the resulting low intensity sub-beams. In general, integration times between a few milliseconds and a second were chosen for SHG detection. Even at the highest intensities in our experiments, the power density in the 3–4 mm2 focal areas was still far below the damage threshold of BBO which is expected in the range of 1–10 GW/cm2.
The two-dimensionally resolved nonlinear autocorrelation yields the distribution of the temporal coherence in space, the direction of rotation (sign) and the order of topological charge of the orbital angular momentum. The nanometer range step width of the interferometer corresponds to a temporal resolution on sub-femtosecond scale. Additionally, the wavefront can either be reconstructed by analysing the deviation compared to a reference wave or by analysing the relative time of arrival of the centers of gravity of the partial wavepackets. It has to be mentioned that the use of nondiffracting sub-beams results in an enhanced angular sensitivity in comparison to the conventional Shack-Hartmann techniques29. Another advantage is the high robustness against distortions because of the well-known self-reconstruction properties of Bessel-like nondiffracting beams30. In the case of nondiffracting beams, the overlap of parts of the wavefront is much reduced compared to arrays of Gaussian sub-beams. Furthermore, pulsed polychromatic Gaussian beams undergo a temporal and spectral dispersion in axial and transversal direction whereas the propagation of ultrashort-pulsed “needle beams”, i.e., the central lobes of pulsed Bessel beams22,23,24 is nondiffracting even in the time domain22,23,24. The flexible shaping of needle beams by pixellated spatial light modulators enables for a correction of aberrations induced by off-axis illumination. The beam ellipticity is corrected by a transformation of the phase axicons from circular to elliptical shape21. In the experiments reported here, the adaptive correction procedure was applied to an array of needle beams for temporal autocorrelation of few-cycle vortex pulses.
It should be noticed that the operation of two identical displays at the same electronic controller (which is designed for up to three RGB channels projector applications) enable a highly synchronous operation and thus to minimize parasitic temporal beating effects.
References
Allen, L., Barnett, S. M. & Padgett, M. Optical angular momentum, (Institute of Physics Publishing. Taylor & Francis, Bristol 2003).
Yao, A. M. & Padgett, M. J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photonics 3, 161–204 (2011).
Malik, M. et al., Direct measurement of a 27-dimensional orbital-angular-momentum state vector. Nature Communications 5, 3115 (2014).
Soskin, M. S., Gorshkov, V. N., Vasnetsov, M. V., Malos, J. T. & Heckenberg, N. R. Topological charge and angular momentum of light beams carrying optical vortices. Phys. Rev. A 56, 4064–4075 (1997).
Lukin, I. Mean intensity of vortex Bessel beams propagating in turbulent atmosphere. Appl. Opt. 53, 3287–3293 (2014).
Padgett, M. & Bowman, R. Tweezers with a twist. Nature Photonics 5, 343–348 (2011).
Ambrosio, A., Marrucci1, L., Borbone, F., Roviello, A. & Maddalena, P. Light-induced spiral mass transport in azo-polymer films under vortex-beam illumination. Nature Communications 3, 989 (2012).
Babiker, M., Bennett, C. R., Andrews, D. L. & Dávila Romero, L. C. Orbital Angular Momentum Exchange in the Interaction of Twisted Light with Molecules. Phys. Rev. Lett. 89, 143601 (2002).
Mair, A., Vaziri, A., Weihs, G. & Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 412, 313–316 (2001).
Wang, J. et al., Terabit free-space data transmission employing orbital angular momentum multiplexing. Nature Photonics 6, 488–496 (2012).
Augustyniak, I., Popiołek-Masajada, A., Masajada, J. & Drobczyński, S. New scanning technique for the optical vortex microscope. Appl. Opt. 51, C117–C124 (2012).
Stoklasa, B., Motka, L., Rehacek, J., Hradil, Z. & Sánchez-Soto, L. L. Wavefront sensing reveals optical coherence. Nature Communications 5, 1–7 (2014).
Akturk, S., Gu, X., Bowlan, P. & Trebino, R. Spatio-temporal couplings in ultrashort laser pulses. J. Opt. 12, 093001 (2010).
Grunwald, R. et al., V. Ultrashort-pulse wavefront autocorrelation. Opt. Lett. 28, 2399–2401 (2003).
Rubino, E. et al., Spatio-temporal amplitude and phase retrieval of space-time coupled ultrashort pulses using the Shackled-FROG technique. Opt. Lett. 34, 3854–3856 (2009).
Bonaretti, F., Faccio, D., Clerici, M., Biegert, J. & Di Trapani, P. Spatiotemporal Amplitude and Phase Retrieval of Bessel-X pulses using a Hartmann-Shack sensor. Opt. Express 17, 9804–9809 (2009).
Valtna-Lukner, H. et al., Direct spatiotemporal measurements of accelerating ultrashort Bessel-type light bullets. Opt. Express 17, 14948–14955 (2009).
Yamane, K., Yang, Z., Toda, Y. & Morita, R. Frequency-resolved measurement of the orbital angular momentum spectrum of femtosecond ultra-broadband optical-vortex pulses based on field reconstruction. New J. Phys. 16, 053020 (2014).
Yamane, K., Toda, Y. & Morita, R. Ultrashort optical-vortex pulse generation in few-cycle regime. Opt. Express 20, 18986 (2012).
Liao, J. et al., Analysis of femtosecond optical vortex beam generated by direct wave-front modulation. Opt. Eng. 52, 106102 (2013).
Bock, M. et al., Reconfigurable wavefront sensor for ultrashort pulses. Opt. Lett. 37, 1154–1156 (2012).
Bock, M., Das, S. K. & Grunwald, R. Ultrashort highly localized wavepackets. Opt. Express 20, 12563–12578 (2012).
Grunwald, R. et al., Ultrashort-pulsed truncated polychromatic Bessel-Gauss beams. Opt. Express 16, 1077–1089 (2008).
Bock, M., Das, S. K. & Grunwald, R. Programmable ultrashort-pulsed flying images. Opt. Express 17, 7465–7478 (2009).
Dholakia, K., Simpson, N. B., Padgett, M. J. & Allen, L. Second-harmonic generation and the orbital angular momentum of light. Phys. Rev. A 54, R3742–R3745 (1996).
Leach, J., Keen, S., Padgett, M. J., Saunter, C. & Love, G. D. Direct measurement of the skew angle of the Poynting vector in a helically phased beam. Opt. Express 14, 11919–11924 (2006).
Allen, L. & Padgett, M. The Orbital Angular Momentum of Light: An Introduction,. in: Twisted Photons: Applications of Light with Orbital Angular Momentum, Eds. Torres, J. P. & Toner, L., (Wiley-VCH, Weinheim, 2011).
Chung, J.–H. & Weiner, A. M. Ambiguity of ultrashort pulse shapes retrieved from the intensity autocorrelation and the power spectrum. IEEE J. Sel. Top. Quant. Electron. 7, 656–666 (2001).
Bock, M., Jahns, J. & Grunwald, R. Few-cycle high-contrast vortex pulses. Opt. Lett. 37, 3804–3806 (2012).
Bouchal, J., Wagner, J. & Chlup, M. Self-reconstruction of a distorted nondiffracting beam. Opt. Comm. 151, 207–211 (1998).
McGloin, D. & Dholakia, K. Bessel beams: diffraction in a new light. Contemp. Physics 46, 15–28 (2005).
Bock, M. et al., Sub-3-cycle vortex pulses of tunable topological charge. Opt. Lett. 38, 3642–3645 (2013).
Acknowledgements
The authors thank G. Steinmeyer (MBI Berlin), P. Saari and H. Valtna-Lukner (University Tartu, Estonia), A. Friberg (Aalto University, Finland and University of Eastern Finland), J. Jahns and M. Musigmann (FernUniversität Hagen), U. Wallrabe and J. Brunne (University Freiburg) and the colleagues from HoloEye Photonics (Berlin), Venteon (Hannover), Andor Technology (Berlin), APE (Berlin) and metrolux (Göttingen) for a fruitful collaboration and the DFG for financial support (Grants GR 1782/13-1, GR 1782/14-1).
Author information
Authors and Affiliations
Contributions
R.G. initiated the activities on adaptive microoptics for ultrashort pulses and was the principal investigator in related projects. M.B. performed a major part of the theoretical and experimental work in frame of his PhD thesis which was supervised by T.E. All three authors contributed essentially to the basic concepts and were directly involved in the preparation of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Grunwald, R., Elsaesser, T. & Bock, M. Spatio-temporal coherence mapping of few-cycle vortex pulses. Sci Rep 4, 7148 (2014). https://doi.org/10.1038/srep07148
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07148
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.