Abstract
The complexity of the frictional dynamics at the microscopic scale makes difficult to identify all of its controlling parameters. Indeed, experiments on sheared elastic bodies have shown that the static friction coefficient depends on loading conditions, the real area of contact along the interfaces and the confining pressure. Here we show, by means of numerical simulations of a 2D Burridge-Knopoff model with a simple local friction law, that the macroscopic friction coefficient depends non-monotonically on the bulk elasticity of the system. This occurs because elastic constants control the geometrical features of the rupture fronts during the stick-slip dynamics, leading to four different ordering regimes characterized by different orientations of the rupture fronts with respect to the external shear direction. We rationalize these results by means of an energetic balance argument.
Similar content being viewed by others
Introduction
Frictional forces between sliding objects convert kinetic energy into heat and act in systems whose size ranges from the nanometer scale, as in some micro and nanomachines, up to the kilometer scale, typical of geophysical processes. The microscopic origin of frictional forces is therefore deeply investigated and strategies to tune their effects are actively sought1,2,3,4,5. In the classical description of frictional processes6, the transition from the static to the sliding regime occurs as the applied shear stress overcomes the product of the normal applied force and the friction coefficient μ (Amontons–Coulomb law). However, experiments conducted in the last decade7,8 have shown that this transition is driven by a local dynamics of frictional interfaces, which occurs well before macroscopic sliding. In addition, studies on the systematic violation of Amontons–Coulomb law and the dependence on the loading conditions have clarified that the static friction coefficient is not a material constant9,10. This is consistent with numerical studies based of 1D11,12,13 spring-block models that have clarified the influence of the loading conditions on the nucleation fronts. In particular they have shown that the friction coefficient decreases with the confining pressure and the system size. While the effect of the elasticity of the slider in the direction perpendicular to the driving one has been recently addressed via the study of 2D spring-block models14, the role of the elasticity of the contact surface has not yet been clarified.
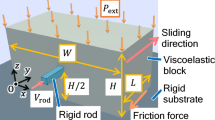
In this study we show that the elasticity of the contact surface influences the features of the fracture fronts leading to a non-monotonic behaviour of the friction coefficient. These results are obtained via numerical simulations of a 2D (xy) spring-block model (Fig. 1a) and are supported by analytical arguments. Our model, fully described in the method section, is a simple variation of the Burridge–Knopoff15,16 (BK) model that is commonly used in seismology to describe a seismic fault under tectonic drive and that reproduces many statistical features of earthquake occurrence17,18,19,20. The model is represented by a series of blocks, interconnected by springs of elastic constant kb and interacting with the substrate with a frictional force characterized by a uniform friction coefficient μs, initially arranged on a two dimensional square lattice of size Lx × Ly.
The 2D Burridge-Knopoff model.
(a) Schematic representation of the model: An elastic layer of red particles connected by yellow springs is in contact with a bottom-flat substrate (gray). The system is driven by an external spring mechanism along the x-direction at constant velocity Vd and each particle is confined by a constant pressure σn. (b) Time dependence of the shear stress σx(t) during the stick-slip dynamics for two systems with different values of ϕ. Filled black squares and open red circles indicate the values of the shear stress that, divided by σn, are used to estimate the macroscopic friction coefficient  . The horizontal dash-dotted (blue) line indicates the value of the stress corresponding to the Amontons-Coulomb threshold.
. The horizontal dash-dotted (blue) line indicates the value of the stress corresponding to the Amontons-Coulomb threshold.
We study its properties as a function of the parameter ϕ = kb/Δkd, where Δkd is the variance of the distribution of the elastic constant kd with which each block is coupled to the drive (see Fig. 1a). Accordingly, ϕ measures the relevance of the elastic heterogeneity, the ϕ → 0 limit corresponding to a system elastically homogeneous. We show that, even if the Amontons–Coulomb law is locally satisfied for each contact, violations at the macroscopic scale are observed, due to the interplay between the elasticity of the material and the local frictional forces. This interplay influences the macroscopic friction coefficient as it determines how the ordering properties of the system change under shear: Stiff systems keep their ordered structure, while soft systems disorder more easily. We report four different shear–induced ordering regimes, each one characterized by rupture fronts with specific geometric features. The macroscopic friction coefficient  does not vary monotonically with the degree of order of the system or with the degree of elastic heterogeneity: Indeed
does not vary monotonically with the degree of order of the system or with the degree of elastic heterogeneity: Indeed  exhibits a minimum when the periodic order of the system is broken in the direction perpendicular to the shear, which occurs at intermediate heterogeneities. This leads to a
exhibits a minimum when the periodic order of the system is broken in the direction perpendicular to the shear, which occurs at intermediate heterogeneities. This leads to a  that is larger both for highly ordered (homogeneous) and highly disordered (heterogeneous) systems. We therefore find a non-monotonic relationship between
that is larger both for highly ordered (homogeneous) and highly disordered (heterogeneous) systems. We therefore find a non-monotonic relationship between  and the ordering of the material which, in our study, is controlled by elastic heterogeneity. More generally, the ordering degree can be affected by different physical mechanisms, such as for instance the jamming or cristalization transitions21,22.
and the ordering of the material which, in our study, is controlled by elastic heterogeneity. More generally, the ordering degree can be affected by different physical mechanisms, such as for instance the jamming or cristalization transitions21,22.
The dynamics exhibits the typical stick-slip behaviour with phases of slow stress accumulation interrupted by an abrupt energy release. Fig. 1b shows for different values of ϕ the time evolution of the shear stress  , where xi(t)−Vdt is the elongation of the i-th particle. The stress drop amplitude exhibits a power law distribution19,20 that can be related to the Gutenberg-Richter law of experimental seismicity. We define the macroscopic friction coefficient as the average over many slips of the steady state shear stress right before failure (symbols in Fig. 1b), divided by the confining pressure
, where xi(t)−Vdt is the elongation of the i-th particle. The stress drop amplitude exhibits a power law distribution19,20 that can be related to the Gutenberg-Richter law of experimental seismicity. We define the macroscopic friction coefficient as the average over many slips of the steady state shear stress right before failure (symbols in Fig. 1b), divided by the confining pressure  . The dependence of
. The dependence of  on ϕ in Fig. 2 is clearly non–monotonic, with a minimum corresponding to a ~ 40/% reduction of the friction coefficient with respect to the microscopic value μs = 0.2. This minimum is observed for all values of N and becomes more pronounced for larger N.
on ϕ in Fig. 2 is clearly non–monotonic, with a minimum corresponding to a ~ 40/% reduction of the friction coefficient with respect to the microscopic value μs = 0.2. This minimum is observed for all values of N and becomes more pronounced for larger N.
The friction coefficion depends non-monotonically on the degree of elastic heterogeneity.
(a) the macroscopic friction coefficient as a function of the parameter ϕ. The value of  is defined as 〈σfail〉/σn, where σfail is the maximum shear stress right before large stress drops (symbols in Fig. 1b) and σn is the confining pressure. Different symbols refer to different system sizes. The dashed vertical lines indicate four regimes: crystalline C, laminar crystalline LC, disorder-parallel DP and disorder-transverse DT. Bottom panel: the asymmetry factor of the clusters of slipping particles as a function of the parameter ϕ.
is defined as 〈σfail〉/σn, where σfail is the maximum shear stress right before large stress drops (symbols in Fig. 1b) and σn is the confining pressure. Different symbols refer to different system sizes. The dashed vertical lines indicate four regimes: crystalline C, laminar crystalline LC, disorder-parallel DP and disorder-transverse DT. Bottom panel: the asymmetry factor of the clusters of slipping particles as a function of the parameter ϕ.
Next, we show that the minimum of  is related to changes of the ordering properties of the elastic surface, and, to this end, we consider the ϕ dependence of the bond–orientation ordering parameter23. This is defined as
is related to changes of the ordering properties of the elastic surface, and, to this end, we consider the ϕ dependence of the bond–orientation ordering parameter23. This is defined as

where the second sum runs over all nj nearest neighbors of particle i and θij measures the orientation of each bond at time t with respect to the shear direction. When the configuration preserves its original ordered square lattice configuration Ψ = 1, whereas in the opposite limit of a fully disordered configuration  . Fig. 3 (inset) shows that as the systems is sheared Ψ(t) decreases from Ψ(0) = 1 to a limiting value Ψ(∞). The main panel shows that this asymptotic value is a continuously decreasing function of ϕ, that approaches its ordered and disordered limits for large and small ϕ, respectively. This behavior is consistently observed for different system sizes N.
. Fig. 3 (inset) shows that as the systems is sheared Ψ(t) decreases from Ψ(0) = 1 to a limiting value Ψ(∞). The main panel shows that this asymptotic value is a continuously decreasing function of ϕ, that approaches its ordered and disordered limits for large and small ϕ, respectively. This behavior is consistently observed for different system sizes N.
The degree of elastic heterogeneities controls the ordering properties of the system.
Main panel: the asymptotic value of Ψ(t) as a function of the parameter ϕ. Systems are initially prepared in the same ordered state. Depending on ϕ, structural changes can occur as revealed by the order parameter, which drops from 1 (rigid bond) to ~0.5 (very elastic bond). Error bars are comparable to symbol sizes. Inset: Time evolution of Ψ(t) for systems with N = 400 and ϕ = 103 (black filled squares), ϕ = 102 (open red circles), ϕ = 10 (green diamonds) and ϕ = 1 (blue triangles).
Concerning the dependence of Ψ on the system size N, we observe that for ϕ ≥ 102 the parameter Ψ(∞) is N independent. Conversely, at smaller ϕ we notice Ψ(∞) is a weakly decreasing function of N, indicating that the larger is N the more disordered is the configuration. This behaviour can be attributed to heterogeneities of the local stress. Indeed, for larger systems the probability to find local instabilities is higher, which favors the occurrence of local rearrangements leading to more disordered configurations. The same argument can be also used to explain the weak decrease of the macroscopic friction with N (Fig. 2a), but does not account for the presence of the minimum in  . Indeed,
. Indeed,  is not a monotonic function of Ψ.
is not a monotonic function of Ψ.
Here we show that  variations can be related to the geometrical properties of clusters of slipping particles. We define as “slipping particle” the one with a displacement in the shear direction larger than a given threshold Sx = 0.01 l, where l is the lattice constant. We observe compact clusters of slipping particles (rupture fronts) whose geometrical features are characterized by their sizes along the direction parallel, lx and perpendicular, ly, to the shear,
variations can be related to the geometrical properties of clusters of slipping particles. We define as “slipping particle” the one with a displacement in the shear direction larger than a given threshold Sx = 0.01 l, where l is the lattice constant. We observe compact clusters of slipping particles (rupture fronts) whose geometrical features are characterized by their sizes along the direction parallel, lx and perpendicular, ly, to the shear,  and
and  . Here, Δxij (Δyij) is the distance between particles i and j along the x (y) direction and the sum is extended to all Nc(Nc − 1) particle couples belonging to a cluster. The normalization factor B = Nc(Nc − 1)/4 insures that for a cluster involving the whole system lx = Lx and ly = Ly.
. Here, Δxij (Δyij) is the distance between particles i and j along the x (y) direction and the sum is extended to all Nc(Nc − 1) particle couples belonging to a cluster. The normalization factor B = Nc(Nc − 1)/4 insures that for a cluster involving the whole system lx = Lx and ly = Ly.
In Fig. 4a we present a parametric plot of ly/Ly vs lx/Lx for four different values of ϕ. Cluster configurations can be distinguished into four classes, determined by ϕ, whose typical shape is reported in Fig. 4b. For  we have the crystalline regime (C), represented by black circles in the region with
we have the crystalline regime (C), represented by black circles in the region with  . In this case, the system behaves as a rigid body and slips involve all particles, keeping the original crystalline order. For smaller value of ϕ we have the laminar crystalline regime (LC, red squares) where
. In this case, the system behaves as a rigid body and slips involve all particles, keeping the original crystalline order. For smaller value of ϕ we have the laminar crystalline regime (LC, red squares) where  and ly with values in the range [1, Ly]. In this regime, a typical slip involves the motion of one or few parallel lines. This is consistent with the ordering features observed in this regime (LC lower panel), characterized by order along the direction of the shear and disorder along the transverse direction. A further reduction of ϕ first breaks order in the shearing direction, giving rise to the disorder–parallel regime (DP, green diamonds) and then fully disorders the system, giving rise to the disorder–transverse regime (DT, blue triangles). The shape of the clusters in both these regions are asymmetric with lx/Lx > ly/Ly in the DP whereas lx/Lx < ly/Ly in the DT. This information can be directly extracted from Fig. 4a where we observe that the DP and the DT regimes respectively populate regions above and below the diagonal. We characterize the asymmetry of the cluster shape comparing their average longitudinal and transverse sizes, lx/ly. As shown in Fig. 2b, this ratio varies non–monotonically with ϕ and has a maximum corresponding to the minimum of
and ly with values in the range [1, Ly]. In this regime, a typical slip involves the motion of one or few parallel lines. This is consistent with the ordering features observed in this regime (LC lower panel), characterized by order along the direction of the shear and disorder along the transverse direction. A further reduction of ϕ first breaks order in the shearing direction, giving rise to the disorder–parallel regime (DP, green diamonds) and then fully disorders the system, giving rise to the disorder–transverse regime (DT, blue triangles). The shape of the clusters in both these regions are asymmetric with lx/Lx > ly/Ly in the DP whereas lx/Lx < ly/Ly in the DT. This information can be directly extracted from Fig. 4a where we observe that the DP and the DT regimes respectively populate regions above and below the diagonal. We characterize the asymmetry of the cluster shape comparing their average longitudinal and transverse sizes, lx/ly. As shown in Fig. 2b, this ratio varies non–monotonically with ϕ and has a maximum corresponding to the minimum of  . This suggests that the lowest value of
. This suggests that the lowest value of  is obtained when slips involve the horizontal displacement of the smallest number of lines.
is obtained when slips involve the horizontal displacement of the smallest number of lines.
The morphology of the clusters of slipping particles depends on the elastic heterogeneitiy.
(a) Scatter plot of the clusters dimensions, along the directions parallel and transverse to the shear, for system having different values of ϕ. By reducing the stiffness of the system we observe regions with different cluster shapes, indicated by the letters C, LC, DP, DT. (b) Schematic representations of the geometry of the clusters corresponding to the regions reported in the scatter plot. Here we show a system of dimension Lx = 20 and Ly = 5, the same behaviour is also observed for larger systems.
An explanation of this result and the presence of different regimes is given by a simple energetic argument. Let us suppose that at given time an amount of energy ER provided by the external drive is relaxed via a slip of length δ such that the relaxed energy is ER ~ kdδ2. This energy can be released through the motion of a rectangular cluster of particles of size nxl × nyl. Assuming that all the particles of the cluster slip rigidly by the same distance, the amount of energy released in the slip comes only from the perimeter particles and is given by

where the Heaviside theta function takes into account that, because of periodic boundaries, if a side of the cluster becomes as large as the system size, the interface contribution vanishes. Eq. 2, in the limit of small slips  , becomes
, becomes

As a consequence, for a rigid system ( ) in order to have ΔE ~ ER the first term in Eq.(3) must be zero (nxl = Lx) and also the condition
) in order to have ΔE ~ ER the first term in Eq.(3) must be zero (nxl = Lx) and also the condition  must be satisfied so that
must be satisfied so that  . This corresponds to the slip of entire rows (C regime in Fig. 4a). However, these slips are possible only if the configuration is ordered. When kb becomes smaller, as indicated by the behavior of Φ (Fig. 3), fluctuations appear in the lattice organization preventing slips in the form of entire rows. In this case, since δ < l, configurations with ny < nx are still energetically favored. This situation corresponds to the LC regime in Fig. 4a. On the other hand, as soon as kb (and ϕ) becomes sufficiently small so that nyl = Ly, the second term in Eq. 3 vanishes and the configurations corresponding to the DT regime in Fig. 4a are energetically favored. Summarizing, slipping clusters show different geometries for decreasing kb, with preferential order along the direction parallel (perpendicular) to the drive at high (low) values of kb. Obviously, the transition from ordered to disordered configurations also depends on the degree of heterogeneity of the local shear stress: for larger values of Δkd the transition is expected at larger values of kb. Moreover, if one changes the shape of the system with Lx ≤ Ly, the DT regime is never observed. The last statement has been verified for systems with different values of the ratio Lx/Ly.
. This corresponds to the slip of entire rows (C regime in Fig. 4a). However, these slips are possible only if the configuration is ordered. When kb becomes smaller, as indicated by the behavior of Φ (Fig. 3), fluctuations appear in the lattice organization preventing slips in the form of entire rows. In this case, since δ < l, configurations with ny < nx are still energetically favored. This situation corresponds to the LC regime in Fig. 4a. On the other hand, as soon as kb (and ϕ) becomes sufficiently small so that nyl = Ly, the second term in Eq. 3 vanishes and the configurations corresponding to the DT regime in Fig. 4a are energetically favored. Summarizing, slipping clusters show different geometries for decreasing kb, with preferential order along the direction parallel (perpendicular) to the drive at high (low) values of kb. Obviously, the transition from ordered to disordered configurations also depends on the degree of heterogeneity of the local shear stress: for larger values of Δkd the transition is expected at larger values of kb. Moreover, if one changes the shape of the system with Lx ≤ Ly, the DT regime is never observed. The last statement has been verified for systems with different values of the ratio Lx/Ly.
In conclusion, we have found that frictional properties depend on the geometry of the rupture fronts, which are determined by the ordering of the contact interface. These features result from interface deformation occurring during the shearing process and thus depend on the elasticity of the material. Future developments will investigate the stability of this scenario by tuning interface ordering through different physical mechanisms.
Methods
We consider a two dimensional BK model, where a layer of particles of mass m is placed on a square lattice with lattice constant l and nearest neighbor particles are connected by harmonic elastic springs with constant kb (Fig. 1a). Each particle i is connected to a plate moving with constant velocity along the x axis by a spring whose stiffness  is uniformly distributed in the range (kd − Δkd, kd + Δkd). Δkd is a parameter allowing to control the heterogeneity of the local shear stress. A granular–like approach24 is used to model the interaction of a particle with the bottom plate. At time t the frictional force acting on a particle is given by
is uniformly distributed in the range (kd − Δkd, kd + Δkd). Δkd is a parameter allowing to control the heterogeneity of the local shear stress. A granular–like approach24 is used to model the interaction of a particle with the bottom plate. At time t the frictional force acting on a particle is given by  , where
, where  is the shear displacement of the particle due to creep motion and t0 the last time of contact formation. Indeed, each contact breaks and reforms as soon as the Amontons–Coulomb threshold criterion
is the shear displacement of the particle due to creep motion and t0 the last time of contact formation. Indeed, each contact breaks and reforms as soon as the Amontons–Coulomb threshold criterion  is violated. Here σn is the confining normal force acting on each grain, A = l2 the lattice cell area and μs the local coefficient of static friction. The grain motion is also damped by a viscous term
is violated. Here σn is the confining normal force acting on each grain, A = l2 the lattice cell area and μs the local coefficient of static friction. The grain motion is also damped by a viscous term  . Mass, spring constants and lengths are expressed in units of m, kd and l, respectively. We fix FN = 5 kdl, μs = 0.2, ke = 10 kd, Δkd = kd, σn = 5 kd/l, Vd = 2 · 10−2 (m/kd)1/2 and γ = 0.2 (kd/m)1/2. These values insure that simulations are in the quasi-static regime. Periodic boundary conditions are considered in both directions. The number of particles N equals the system size Lx × Ly, with Ly = Lx/4 and assumes the following values, N = 100, 400, 900. We have investigated the frictional properties of the system as a function of the parameter ϕ = kb/Δkd that we vary by changing kb. This parameter measures the relevance of the stiffness of the system with respect to the heterogeneity of the shearing forces.
. Mass, spring constants and lengths are expressed in units of m, kd and l, respectively. We fix FN = 5 kdl, μs = 0.2, ke = 10 kd, Δkd = kd, σn = 5 kd/l, Vd = 2 · 10−2 (m/kd)1/2 and γ = 0.2 (kd/m)1/2. These values insure that simulations are in the quasi-static regime. Periodic boundary conditions are considered in both directions. The number of particles N equals the system size Lx × Ly, with Ly = Lx/4 and assumes the following values, N = 100, 400, 900. We have investigated the frictional properties of the system as a function of the parameter ϕ = kb/Δkd that we vary by changing kb. This parameter measures the relevance of the stiffness of the system with respect to the heterogeneity of the shearing forces.
References
Dowson, D. History of Tribology (Longman, New York, 1979).
Baumberger, T. & Caroli, C. Solid friction from stick slip down to pinning and aging. Adv. in Phys. 55, 279 (2006).
Capozza, R., Vanossi, A., Vezzani, A. & Zapperi, S. Suppression of friction by mechanical vibrations. Phys. Rev. Lett. 103, 085502 (2009).
Vanossi, A., Manini, N., Urbakh, M., Zapperi, S. & Tosatti, E. Modeling friction: from nanoscale to mesoscale. Rev. of Mod. Phys. 85, 529 (2013).
Capozza, R., Barel, I. & Urbakh, M. Probing and tuning frictional aging at the nanoscale. Sci. Rep. 3, 1896 (2013).
Bowden, F. P. & Tabor, D. The Friction and Lubrication of Solids (Oxford University Press, New York., 1950).
Rubinstein, S. M., Cohen, G. & Fineberg, J. Dynamics of precursors to frictional sliding. Phys. Rev. Lett. 98, 226103 (2007).
Ben-David, O., Rubinstein, S. M. & Fineberg, J. Slip-stick: The evolution of frictional strength. Nature 76, 463 (2010).
Otsuki, M. & Matsukawa, H. Systematic breakdown of amontons' law of friction for an elastic object locally obeying amontons' law. Sci. Rep. 3, 1586 (2013).
Ben-David, O. & Fineberg, J. Static friction coefficient is not a material constant. Phys. Rev. Lett. 106, 254301 (2011).
Maegawa, S., Suzuki, A. & Nakano, K. Precursors of global slip in a longitudinal line contact under non-uniform normal loading. Tribol. Lett. 38, 313 (2010).
Braun, O. M., Barel, I. & Urbakh, M. Dynamics of transition from static to kinetic friction. Phys. Rev. Lett. 103, 194301 (2009).
Amundsen, D. S., Scheibert, J., Thogersen, K., Tromborg, J. & Malthe-Sorenssen, A. 1d model of precursors to frictional stick-slip motion allowing for robust comparison with experiments. Tribol. Lett. 45, 357 (2012).
Tromborg, J., Scheibert, J., Amundsen, D. S., Thogersen, K. & Malthe-Sorenssen, A. Transition from static to kinetic friction: insights from a 2d model. Phys. Rev. Lett. 107, 07431 (2011).
Burridge, R. & Knopoff, L. Model and theoretical seismicity. Bull. Seismol. Soc. Am. 57, 341 (1967).
Carlson, J. & Langer, J. Properties of earthquakes generated by fault dynamics. Phys. Rev. Lett. 62, 2632 (1989).
Mori, T. & Kawamura, H. Simulation study of the two-dimensional burridge-knopoff model of earthquakes. J. Geophys. Res. 113, B06301 (2008).
Mori, T. & Kawamura, H. Simulation study of earthquakes based on the two-dimensional burridge-knopoff model with long-range interactions. Phys. Rev. E 77, 051123 (2008).
Ciamarra, M. P., Lippiello, E., Godano, C. & de Arcangelis, L. Unjamming dynamics: the micromechanics of a seismic fault model. Phys. Rev. Lett. 104, 238001 (2010).
Ciamarra, M. P., Lippiello, E., de Arcangelis, L. & Godano, C. Statistics of slipping event sizes in granular seismic fault models. Europhys. Lett. 95, 54002 (2011).
Jin, Y., Puckett, J. G. & Makse, H. A. Statistical theory of correlations in random packings of hard particles. Phys. Rev. E 89, 052207 (2014).
Bhushan, B., Israelachvili, J. N. & Landman, U. Nanotribology: friction, wear and lubrication at the atomic scale. Nature 374, 607 (1994).
Nelson, D. R. & Halperin, B. I. Dislocation-mediated melting in two dimensions. Phys. Rev. B 19, 2457 (1979).
Silbert, L. E. et al. Granular flow down an inclined plane: Bagnold scaling and rheology. Phys. Rev. E 64, 051302 (2001).
Acknowledgements
We acknowledge the financial support of MIUR FIRB RBFR081IUK (2008) and MIUR PRIN 20098ZPTW7 (2009). L.S. is financed by the MASTRI EXCELLENCE NETWORK of the Campania region.
Author information
Authors and Affiliations
Contributions
F.G. and L.S. produced numerical simulations and prepared all the figures. L.dA., M.P.C. and E.L. wrote the main manuscript text. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Giacco, F., Ciamarra, M., Saggese, L. et al. Non-monotonic dependence of the friction coefficient on heterogeneous stiffness. Sci Rep 4, 6772 (2014). https://doi.org/10.1038/srep06772
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep06772
This article is cited by
-
Exploiting surface textures dynamics for dry friction control
Nonlinear Dynamics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.