Abstract
Chemical reactions can be described by an energy diagram along a reaction coordinate in which an activation barrier limits the rate at which reactants can be transformed into products. This reaction impedance can be overcome by reducing the magnitude of the barrier through the use of catalysis, increasing the thermal energy of the system, or through macroscopic mechanical processes. Here, we demonstrate direct molecular-scale control of a reaction through the precise application of opto-mechanical work. The method uses optical gradient forces generated in the evanescent field surrounding hybrid photonic-plasmonic structures to drive an otherwise unlikely adsorption reaction between proteins and carbon nanotubes. The adsorption of immunoglobulins on carbon nanotubes is used as a model reaction and investigated with an extended DLVO theory. The technique is also used to force a Förster resonance energy transfer between fluorophores on mismatched immunoglobulin proteins and is expected to lead to novel forms of chemical synthesis.
Similar content being viewed by others
Introduction
The behavior of molecules in solution is governed by energy barriers, potential wells and stochastic events. The progression of a chemical reaction is often described in terms of a reaction energy diagram that reflects changes in free energy along an abstractly defined reaction coordinate. In this framework, a reaction will occur if the reactants can acquire the necessary energy to overcome the activation energy barrier and proceed along the reaction coordinate towards the product state. This process can be accelerated by applying bulk kinetic energy in the form of heat, which raises the energy of the reactants relative to this barrier1,2. This can have a number of adverse effects, such as the acceleration of other undesired reactions decreasing the chemical efficiency and the denaturation of temperature-sensitive molecules, so alternative techniques are often necessary3.
To counter the negative effects of heating, methods such as catalysis are used which reduce the activation energy by altering the intermediate states instead of adding energy to the reactants. In a catalytic process, a catalyst is introduced as an alternate reaction intermediate that changes the reaction pathway to one with a lower activation energy barrier4. While catalysis can greatly improve the rate of a reaction, it is ill-suited for studying the dynamics of a reaction because the reaction diagram itself is altered with a catalyst present5. Moreover, a particular catalyst will only accelerate certain reactions and will be dependent on the molecules involved5. More recently, there has also been significant research into mechanical chemistry, in which mechanical forces are used to manipulate or induce chemical reactions2,6,7,8. This is typically achieved with bulk mechanical processes such as grinding8 and milling2. By grinding particles together with high force, mechanical stresses can cause deformations in the surface structure which increase reactivity7. Reactions can also be similarly driven in bulk solution with vibrations, e.g. from ultrasonication7. On a more local level, individual nanoscale molecules such as DNA9 and proteins10 can be mechanically stretched and unfolded using forces generated by an AFM cantilever or by tethering them to larger nanoparticles, such as glass beads, which can then be pulled using optical or magnetic tweezers9.
An alternative paradigm that uses mechanical work generated by near-field optical forces to overcome the activation barrier of a reaction without catalysis is demonstrated here. Light and electro-magnetism in general, have been used previously to provide energy to certain reactions11 or even to dope catalysts12 without requiring a physical presence in the solution. Energy from absorbed photons has also been used to excite electrons to higher energy levels where they can react more readily or favor a specific conformation. Unlike thermal processes, however, these photochemical techniques require specific functional groups and electronic configurations and do not generalize to other reactions. The opto-mechanical force demonstrated here is generated by polarizing dielectric particles and does not require any specific chemical properties. Moreover, the force is strong enough to drive nanoscale particles without the need for an external tether which might change the conformation of the molecules of interest.
Results
In this work, light-mediated mechanical forces are used to locally modify the energy diagram of a protein adsorption reaction along the reaction coordinate without the use of a catalyst. The technique relies on optical gradient forces acting on biomolecules in solution and on the adsorption of these molecules to hydrophobic surfaces. The exploitation of light to affect the motion of micrometer to nanometer scale particles was first pioneered by Ashkin when he invented optical tweezers in 198613. Since then, the optical gradient force has found numerous applications in optics, physics14,15 and biology16. Efforts to trap smaller molecules in solution have led to the recent development of molecular tweezers17,18 which allow proteins and other small elements to be trapped by nano-optics and nano-photonic structures. Non-mechanical aspects of the interaction of nano-optics with molecules have also been investigated. For example, researchers have demonstrated the possibility to optically resolve molecular bonds with sub-nanometer resolution19. Other researchers have recently demonstrated the possibility to observe chemical reactions as they happen with nano-optical elements20. The present work builds on these efforts and is the first demonstration of the use of the electromagnetic gradient force, the mechanical force arising from the confinement of an electromagnetic field, to provide molecules with the necessary mechanical work to overcome the activation energy barrier standing between reactants and products in a reaction diagram.
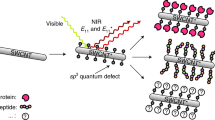
In our first illustration of the use of these opto-mechanical forces to induce chemical reactions, we demonstrate the ability to control the adsorption of different forms of immunoglobulin proteins (Ig) onto carbon nanotubes (CNTs). Multi-wall CNTs offer proteins a surface onto which they can adsorb (when forced into sufficient proximity) and also exhibit metallic properties which can expand and enhance electromagnetic fields21,22. When incident optical power couples onto the carbon nanotubes, an amplified evanescent field extends into the region surrounding the nanotube. This decaying field presents a strong electromagnetic intensity gradient which induces an optical gradient force on proteins in the vicinity of the CNT, as illustrated in Fig. 1. Except at very short distances, the reaction coordinate for the adsorption reaction is considered to be the separation between the two molecules, the same axis along which the optical gradient force acts. In the absence of these forces, the adsorption of the protein is prevented by double layer repulsion and by the presence of surfactant and blocking molecules at the surface of the CNTs. The adsorption experiments are performed at various incident optical powers and the optical power at which the gradient force is just strong enough to pull the molecule through the activation energy barrier is recorded in each case.
Schematic representation of the experiment.
(a) Reaction diagram for the adsorption reaction. When the work done on the molecule by the optical force is large enough, the potential barrier corresponding to the DLVO repulsion is overcome. At very short distances between the nanotube and the protein, the reaction coordinate is no longer well approximated by the intermolecular distance and optical forces become negligible compared to binding forces. (b) Multi-walled carbon nanotube (MWCNT) on a waveguide. Few to no proteins (green Y) adsorb on the MWCNT in the absence of the electromagnetic potential. (c) With light shining, the metallic structure of the nanotube enhances the light intensity (red). Proteins now adsorb onto the nanotube. (d) SEM image of a MWCNT on a silicon waveguide.
Analytical Theory
The reaction diagram was analytically modeled with an extended Derjaguin-Landau-Verwey-Overbeek (DLVO) theory for simplicity, despite some of its known shortcomings23. The DLVO potential energy, derived assuming a constant surface potential and extended to include hydrophobic interactions between a small sphere and a cylinder, is given by24,25

In this equation, UDLVO is the potential energy of the colloidal interaction, R is the gas constant, kB is the Boltzmann constant, T is the temperature, c0 is the bulk ionic concentration, λD is the Debye length calculated as λ2 = RTε/F2c0 where ε is the buffer permittivity and F is the Faraday constant, z is the distance between the molecules, A is the Hamaker constant, Rp is the radius of the protein, Ch and D0 are parameters in the hydrophobic extension of the theory and γ0,p and γ0,CNT are the surface charge densities of protein and CNTs, respectively. The DLVO theory was further extended in equation (2) to include the effects of the surfactant molecule and the mechanical action of light. Along the reaction coordinate, the energy diagram is now given by

Where U is the total potential energy of the reaction including optical forces, α is the polarizability of the protein, Lev is the evanescent field length, E0 is the electromagnetic field strength, ST is the Soret coefficient of the protein, N is the number of surfactant molecules that the protein needs to remove in order to dock on the nanotube, EA is the activation energy required to remove the surfactant molecule and χ is a Heaviside step function supported where the surfactant molecule resides. The second term of the equation is the electromagnetic potential well arising from the gradient force and the third term corresponds to the thermophoretic effect26. The last term is introduced here and intended to model the presence of surfactant and blocking buffer molecules at the nanotube surface which are used in both dispersing the nanotubes in solution and preventing non-specific adsorption.
Controlled antibody adsorption
Experimentally, a silicon waveguide is used to transport the 1550 nm laser light to the nanotube immobilized on the waveguide surface and the proteins are delivered through a microfluidic channel mounted on top of the chip, as drawn in Fig. S1 of the Supplementary Information. The light from the waveguide evanescently couples to the carbon nanotubes where it is amplified, forming a strong optical nanotweezer device which attracts nearby dielectric particles, as demonstrated in previous work22. In the present work, the optical gradient force arising from this light confinement is used to perform work along the reaction coordinate of an energy diagram to overcome the potential barrier which ordinarily prevents the reaction from occurring, as shown in Fig. 1(a). (For a schematic of the optical intensity near a CNT, see Supplemental Fig. S2.) Schematic views of the nanotube before and after the optical forces are used to drive the adsorption reaction are presented in Fig. 1(b),(c). The threshold power at which the adsorption starts is measured experimentally by observing the adsorption of the fluorescently tagged molecules and is taken to represent the height of the energy barrier in the DLVO theory. Since changes in experimental conditions could have a substantial influence on the height of the potential barrier, the solution temperature and flow rate were held constant all across experiments at 294 K and 105 μL/hr, respectively. A control experiment was also performed where the solution was heated externally via hotplate to rule out the possibility of a thermal mechanism for the adsorption. In this experiment, the temperature was varied from 294 K to 333 K without any observable adsorption onto the nanotube.
The opto-mechanical adsorption of fluorescently tagged IgM proteins onto CNTs is presented in Fig. 2. Prior to each experiment, multi-wall carbon nanotubes (outer radius 110–170 nm) were first immobilized on the silicon waveguides and exposed to blocking buffer (Starting Block TBS or SEA Block) for two hours. A dilution of 0.5 μg/ml of Alexa 488 conjugated IgM proteins in a dilution of Phosphate Buffered Saline (PBS, dH2O, 0.5% Tween 20) was prepared prior to each experiment. Time-lapse fluorescent images of the nanotubes in the IgM solution were captured using a CCD camera with a one second exposure for one minute intervals every few minutes. In between these collection periods, the camera shutter was closed to prevent photobleaching from prolonged continuous exposure to the mercury lamp excitation. At the beginning of the experiment, no background fluorescence is visible, indicating that few to no IgM molecules are adsorbed on the nanotube's surface, as seen in Fig. 2(a). The input laser power is increased at approximately 10 minute intervals and no adsorption is observed until it reaches the threshold power, as shown in Fig. 2(a–d). The readout power of the 1550 nm light is recorded by an optical power meter at the output of the chip and the total fluorescent intensity on the CNT is determined from the captured images using ImageJ. (For a schematic of the microchip within the imaging setup, see Supplementary Fig. S3.) The traces of the readout power and of the fluorescent signal are plotted in Fig. 2(e) as a function of time for two experiments in PBS 1× (red) and two in PBS 0.1× (blue). The colored dots represent the measured fluorescent intensity and the dashed lines are the power trace throughout the experiments. The steady state intensity, measured at the end of each power step, is also plotted in Fig. 2(f) as a function of the input power demonstrating that the adsorption only begins after the power reached a certain power threshold. The measured threshold power depends on the coupling from the fiber to the waveguide and from the waveguide to the CNT which can vary from experiment to experiment. The measured powers are normalized by the power necessary to bring the temperature up from the bulk temperature to boiling, which always occurs at a given power density coupled in the carbon nanotube. Linearity of the heat and electromagnetic equations allow for such a normalization which therefore allows for direct comparison of experiments irrespective of the coupling conditions.
Aggregation of Alexa Fluor 488-conjugated IgM on a nanotube observed under fluorescence microscopy.
(a–d) Fluorescent images before (a) and after (b–d) reaching the power threshold for adsorption. The bright spot is the aggregate. Each image is taken reaching steady state at the input power. (e) Plot of the measured fluorescent intensity in PBS 0.1× (blue dots) and in PBS 1× (red dots). Dashed lines at the bottom represent the normalized power output. Vertical bars mark the time step when fluorescence begins to increase. (f) Plot of the steady state intensity as a function of coupled power for the same data sets as in (e).
The effect of the Debye length on the activation energy of the adsorption reaction was measured by manipulating the concentration of the PBS buffer. The power threshold at which the adsorption begins was recorded and is plotted in Fig. 3(a) as a function of the Debye length for experiments with two polarizations (green and red) along with the fitted activation energy as calculated from DLVO theory for different ionic strengths (solid curve). According to Equation (1), towards higher ionic strengths, or lower Debye lengths, the activation energy of the adsorption reaction should decrease due to dispersion forces. The applied electromagnetic potential necessary to overcome the activation energy and drive the reaction in Equation (2) should therefore decrease as well. Ignoring the effects of thermophoresis, the input optical power threshold is expected to map to the activation energy from Equation (1). The activation energy is in qualitative agreement with the DLVO model used here at low Debye lengths (solid lines). Differences between the measured barrier height and the DLVO fit, particularly at higher Debye lengths (dashed lines), are attributed to the failure of the model's assumptions and to changes in surface potential resulting from changes in pH27. The energy barrier was also measured for different immunoglobulin proteins as presented in Fig 3(b) for two polarizations (green and red). Equation (2) indicates that the potential well depth is proportional to the polarizability, α, of the molecule which in turn scales with the mass, assuming a similar chemical composition. It is to be expected, therefore, that more optical power is necessary to overcome the same potential barrier for proteins with lower molecular weights. Figure 3(b) presents the measured power threshold in PBS 10× for IgG, secretory IgA and IgM with molecular weights 160 kDa, 385 kDa and 970 kDa respectively. As expected, the necessary input power increases as the mass of the molecule decreases. The dashed curve presents the expected power threshold in the case where the potential barrier is the same across species.
Power threshold at various salinities and protein masses for two polarizations of the incident light (green and red).
(a) Measured power threshold for accumulation as a function of the Debye length of the buffer (colored markers) and estimate of the energy barrier height from the DLVO model (solid line) below 0.75 nm. Dashed lines: extension of the fit to the regions where the model's assumptions fail. (b) Measured power threshold for accumulation as a function of the molecular weight of the immunoglobulin species used (colored dots). Dashed line: expected power threshold when the potential barrier is the same across species. Error bars: one standard deviation plus 5% lower bar to account for the discrete power steps.
Optically Driven FRET
The opto-mechanical chemistry technique was also used to drive a reaction between two mismatched immunoglobulin proteins. By forcing the molecules close together, a Förster Resonance Energy Transfer (FRET) signal was obtained between a donor (Alexa Fluor 488) and an acceptor (TRITC) conjugated to a goat anti-mouse IgM and a normal goat IgG, respectively. In the absence of optical forces, electrostatic repulsion would prevent the donor and acceptor from being close enough for a FRET reaction to occur. The observed FRET signal indicates that the opto-mechanical forces can bring the molecules into closer proximity than could otherwise be achieved. By creating a high local concentration of molecules in close proximity, the corresponding increase in collisions can force reactions or other exchanges between molecules which are otherwise unlikely to occur28, as illustrated in Fig. 4(a). The acceptor molecule was first immobilized on the CNT, as seen in Fig. 4(c) and a blocking buffer (Starting Block TBS) was used overnight. Little to no background was found for the donor and FRET filters as seen in Fig. 4 (e),(g) (some background is due to the blocking buffer and Tween 20). When the optical trap is activated, the donor-conjugated IgM starts aggregating (Fig. 4(f)) and a FRET signal arises from the forced proximity between the donor and the acceptor, which can be seen in Fig. 4(h). The intensity of the acceptor channel decreases steadily over the course of the FRET experiment due to photobleaching, as seen in Fig. 4(d).
Forced proximity of mismatched IgM proteins.
(a) Schematic. Black circle: useful collisions in solutions are rare. Red circle: in the potential well of the MWCNT, trapped molecules are confined to a smaller region making rare processes more common and more observable. (b) Trace of the intensity of the acceptor (red triangles), donor (green circles) and FRET (blue squares) fluorescent channels. Initially, the acceptor bleaches while donor and FRET channels remain unchanged. When accumulation starts, the donor and FRET signals sharply increase. (c-h) Pseudo-color contrast adjusted fluorescent images before (left column) and after (right column) accumulation. (c–d) acceptor channel. (e–f) donor channel. (g–h) FRET channel.
Discussion
In this work, we have presented experimental evidence that near-field optical forces can be used to drive unlikely chemical reactions. Using fluorescently labeled antibodies, we find negligible protein adsorption to the carbon nanotube substrate without optical forces. When sufficient optical power is supplied from the laser, however, adsorption occurs rapidly and there is a sharp increase in the fluorescence signal. To account for this effect, we developed a novel extended form of the well-known DLVO theory of colloidal interactions which also accounts for opto-mechanical forces. As the model suggests, the repulsive potential due to the double layer charge will prevent the adsorption reaction from occurring under ordinary circumstances. When enough optical power is added, however, the attractive potential counterbalances the repulsive electric potential and the proteins are pulled into very close range where hydrophobic forces dominate.
To confirm this effect, a series of experiments were performed to test the potential energy landscape under various conditions. By varying the salt concentration of the solution, we find that the power required to drive adsorption does vary as predicted by the extended DLVO model up to a Debye length of around 0.6 nm, but then decreases again for lower salts. The breakdown in the predicted trend is due at least in part to the limitations of the standard DLVO model in this regime. The DLVO theory treats the repulsive electrostatic forces and attractive Van der Waals forces as separable, an assumption which is not valid in biological salt concentrations29. Moreover, it neglects specific ion effects which can be particularly important in a salt mixture (like PBS)23. For this reason, the predictions of the theory are not expected to capture all of the system dynamics over the range of concentrations used; nevertheless, it is valuable to compare the driven adsorption with a standard model of colloidal interactions to see where the predictions hold and where they do not. Despite the limited success of the model, the trend does match well with known qualitative properties of protein suspensions. As the salt concentration initially increases, the additional ions screen the charges on the proteins and reduce the attractive forces, a phenomenon known as “salting in” the proteins30. Because the strength of the optical force is well-understood, opto-mechanically driven reactions can be used to probe the barrier height of a reaction even in cases where there is not a good analytic prediction. Because the polarizability of the molecule is linear with the mass, the required optical power is expected to increase as the mass of the antibody decreases if the adsorption is driven by the optical gradient force. Despite the breakdown in the salinity prediction, the mass trend agrees with this prediction well, suggesting that the dominant factor is the optical force. (For a discussion of additional thermal forces, see the Supplementary Information.) An additional FRET experiment is performed which further supports that the antibodies are being forced over the repulsive barrier, as a FRET signal should only be visible if the donor and receptor are in very close proximity and does not occur in bulk solution without optical power.
From these results, we conclude that we have demonstrated for the first time the controlled driving of a reaction on a molecular scale using optically-mediated mechanical forces. Although the present work investigates protein adsorption to carbon nanostructures, this effect would generalize well to many other reactions, as the optical gradient force will act on any polarizable particle in solution and does not require a specific electronic structure. Along with other emerging methods19,31, this work is part of the changing paradigm challenging established means of interaction with molecules. It offers a new approach to study molecular reactions, develop methods in surface sciences and optofluidics32,33,34 and study reaction engineering and may also provide opportunities in studying the structure-function relationship in large proteins or molecular clusters and in molecular mechanics.
Methods
The chip is composed of a silicon waveguide on a 3 μm SiO2 on 500 μm Si wafer. The silicon photonic waveguides were fabricated using electron beam lithography techniques at the Cornell Nanoscale Facility. A microfluidic channel consisting of a glass coverslip, parafilm walls and PDMS inlets/outlets was mounted on the chips prior to each experiment. To make the microfluidics, a rectangular channel was cut out from a single piece of parafilm using a CO2 laser cutter. A glass coverslip with holes drilled at both ends was placed on top of the parafilm and PDMS inlet and outlet blocks were attached at both ends using oxygen plasma bonding. The silicon chips were cleaned overnight in Nanostrip (Cyantek) between experiments to remove debris and parafilm residue. The 1550 nm light from a tunable laser (ANDO AQ4321) was amplified with an erbium doped fiber amplifier, delivered to the chip by a lensed fiber and brought into physical contact with the chip through end-fire coupling to minimize power fluctuations. The chip was mounted on a microscope stage equipped for bright field and epi-fluorescence (CCD camera: Hamamatsu C4742-80-12AG). The CNT solutions were prepared by adding 5 mg of uncoated 0.01% MWCNT powder (outer radius 110–170 nm, Sigma-Aldrich product # 659258) and 0.5% Tween 20 to 10 mL heavy water and sonicating before each experiment for 20 minutes to inhibit aggregation. Fresh dilutions of PBS were also sonicated with 0.5% Tween 20 for 10 minutes prior to each experiment and the pH of the buffer was kept between 6.8 and 7.3 to optimize Ig integrity. Alexa Fluor 488-conjugated IgM (Life Technologies), TRITC-conjugated IgG (Millipore) and FITC-conjugated sIgA (Sigma-Aldrich), were diluted to 1 μg/ml in PBS before each experiment. After adsorbing the CNT to the waveguide to form the trap, the protein solutions were flowed into the channel at a constant rate of 105 μL/hr to replenish proteins and prevent the reaction rate from being limited by diffusion. The masses of the molecules were taken from the data sheets supplied by the vendors. After each experiment, the boiling power was measured using dark field microscopy and used to normalize each power curve. In the FRET experiment, a FRET cube was assembled to block the emission of the donor and the excitation of the acceptor.
References
Konôpka, M. et al. Mechanochemistry and Thermochemistry are Different: Stress-Induced Strengthening of Chemical Bonds. Phys. Rev. Lett. 100, 115503 (2008).
Takacs, L. Mechanochemistry and the Other Branches of Chemistry: Similarities and Differences. Acta Phys. Pol. A 121 (2012).
Drexler, K. E. Nanosystems: Molecular machinery, manufacturing and computation. (John Wiley & Sons, New York, 1992).
Chorkendorff, I. & Niemantsverdriet, J. W. Concepts of modern catalysis and kinetics. (Wiley-Vch, 2006).
Masel, R. I. Chemical kinetics and catalysis. (Wiley-Interscience, New York, 2001).
Hickenboth, C. R. et al. Biasing reaction pathways with mechanical force. Nature 446, 423–427 (2007).
Ausman, K. D., Rohrs, H. W., Yu, M. & Ruoff, R. S. Nanostressing and mechanochemistry. Nanotechnology 10, 258 (1999).
Venkataraman, K. S. & Narayanan, K. S. Energetics of collision between grinding media in ball mills and mechanochemical effects. Powder Technol. 96, 190–201, 10.1016/S0032-5910(97)03368-8 (1998).
Williams, M. C. & Rouzina, I. Force spectroscopy of single DNA and RNA molecules. Curr. Opin. Struc. Biol. 12, 330–336 (2002).
Rounsevell, R., Forman, J. R. & Clarke, J. Atomic force microscopy: mechanical unfolding of proteins. Methods 34, 100–111, 10.1016/j.ymeth.2004.03.007 (2004).
Fox, M. A. & Dulay, M. T. Heterogenous Photocatalysis. Chem. Rev. 93, 341–357, 10.1021/cr00017a016 (1993).
Christopher, P., Xin, H. L. & Linic, S. Visible-light-enhanced catalytic oxidation reactions on plasmonic silver nanostructures. Nat. Chem. 3, 467–472, 10.1038/Nchem.1032 (2011).
Ashkin, A., Dziedzic, J. M., Bjorkholm, J. E. & Chu, S. Observation of a Single-Beam Gradient Force Optical Trap for Dielectric Particles. Opt. Lett. 11, 288–290 (1986).
Deotare, P. B. et al. All optical reconfiguration of optomechanical filters. Nat. Commun. 3, 846 (2012).
Kippenberg, T. J. & Vahala, K. J. Cavity opto-mechanics. Opt. Express 15, 17172–17205, 10.1364/Oe.15.017172 (2007).
Block, S. M., Goldstein, L. S. B. & Schnapp, B. J. Bead movement by single kinesin molecules studied with optical tweezers. Nature 348, 348–352 (1990).
Pang, Y. & Gordon, R. Optical trapping of a single protein. Nano Lett. 12, 402–406 (2011).
Chen, Y.-F., Serey, X., Sarkar, R., Chen, P. & Erickson, D. Controlled photonic manipulation of proteins and other nanomaterials. Nano Lett. 12, 1633–1637 (2012).
Zhang, R. et al. Chemical mapping of a single molecule by plasmon-enhanced Raman scattering. Nature 498, 82–86, 10.1038/Nature12151 (2013).
Al Balushi, A. A., Zehtabi-Oskuie, A. & Gordon, R. Observing single protein binding by optical transmission through a double nanohole aperture in a metal film. Biomed. Opt. Express 4, 1504–1511 (2013).
Novotny, L. & Hecht, B. Principles of nano-optics. (Cambridge University Press, 2006).
O'Dell, D., Serey, X. & Erickson, D. Self-assembled photonic-plasmonic nanotweezers for directed self-assembly of hybrid nanostructures. Appl. Phys. Lett. 104, 043112–043115 (2014).
Boström, M., Williams, D. R. M. & Ninham, B. W. Specific Ion Effects: Why DLVO Theory Fails for Biology and Colloid Systems. Phys. Rev. Lett. 87, 168103 (2001).
Israelachvili, J. & Pashley, R. The hydrophobic interaction is long range, decaying exponentially with distance. Nature 300, 341–342 (1982)
Li, K. & Chen, Y. Evaluation of DLVO interaction between a sphere and a cylinder. Colloid Surface A 415, 218–229 (2012).
Serey, X., Mandal, S., Chen, Y.-F. & Erickson, D. DNA transport and delivery in thermal gradients near optofluidic resonators. Phys. Rev. Lett. 108, 048102 (2012).
Stafiej, A. & Pyrzynska, K. Adsorption of heavy metal ions with carbon nanotubes. Sep. Purif. Technol. 58, 49–52, 10.1016/j.seppur.2007.07.008 (2007).
Shannon, R. J., Blitz, M. A., Goddard, A. & Heard, D. E. Accelerated chemistry in the reaction between the hydroxyl radical and methanol at interstellar temperatures facilitated by tunnelling. Nat. Chem. 5, 745–749 (2013).
Ninham, B. W. On progress in forces since the DLVO theory. Adv. Colloid Interfac. 83, 1–17, 10.1016/S0001-8686(99)00008-1 (1999).
Kalra, A., Tugcu, N., Cramer, S. M. & Garde, S. Salting-in and salting-out of hydrophobic solutes in aqueous salt solutions. J. Phys. Chem. B 105, 6380–6386 (2001).
Takase, M. et al. Selection-rule breakdown in plasmon-induced electronic excitation of an isolated single-walled carbon nanotube. Nat. Photonics 7, 550–554, 10.1038/nphoton.2013.129 (2013).
Psaltis, D., Quake, S. R. & Yang, C. H. Developing optofluidic technology through the fusion of microfluidics and optics. Nature 442, 381–386 (2006).
Schmidt, H. & Hawkins, A. R. The photonic integration of non-solid media using optofluidics. Nat. Photonics 5, 598–604, 10.1038/nphoton.2011.163 (2011).
Fan, X. D. & White, I. M. Optofluidic microsystems for chemical and biological analysis. Nat. Photonics 5, 591–597, 10.1038/nphoton.2011.206 (2011).
Acknowledgements
The authors would like to thank Roald Hoffmann, Peng Chen, Perry Schein and Alex Barbati for discussion on the modeling, Mo Chen for discussion on adsorption chemistry and Matthew Mancuso for help in the FITC-conjugation of sIgA. The experiments and theory related to the carbon nanotube trapping and absorption reaction were supported by the U.S. Department of Energy Office of Basic Science under Grant DE-SC0003935. The FRET experiments were supported by the National Institutes of Health under grant 1R01GM106420. This work was performed in part at the Cornell NanoScale Facility, a member of the National Nanotechnology Infrastructure Network, which is supported by the National Science Foundation (Grant ECS-0335765). The authors appreciate access and the use of the facilities of the Nanobiotechnology Center (NBTC), an STC Program of the National Science Foundation under Agreement No. ECS-9876771.
Author information
Authors and Affiliations
Contributions
X.S. designed the research and fabricated the silicon chips. X.S., D.O. and P.K. performed the experiments and X.S. and D.O. analyzed the data. X.S., D.O. and D.E. wrote the manuscript. All authors discussed the results and commented on the manuscript. D.E. supervised the research.
Ethics declarations
Competing interests
Yes there is potential Competing Interest. D.E. has an equity interest in a company that is commercializing optofluidics technology similar to that used in this work.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
O'Dell, D., Serey, X., Kang, P. et al. Localized Opto-Mechanical Control of Protein Adsorption onto Carbon Nanotubes. Sci Rep 4, 6707 (2014). https://doi.org/10.1038/srep06707
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep06707
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.