Abstract
Reversible computing has been studied since Rolf Landauer advanced the argument that has come to be known as Landauer's principle. This principle states that there is no minimum energy dissipation for logic operations in reversible computing, because it is not accompanied by reductions in information entropy. However, until now, no practical reversible logic gates have been demonstrated. One of the problems is that reversible logic gates must be built by using extremely energy-efficient logic devices. Another difficulty is that reversible logic gates must be both logically and physically reversible. Here we propose the first practical reversible logic gate using adiabatic superconducting devices and experimentally demonstrate the logical and physical reversibility of the gate. Additionally, we estimate the energy dissipation of the gate and discuss the minimum energy dissipation required for reversible logic operations. It is expected that the results of this study will enable reversible computing to move from the theoretical stage into practical usage.
Similar content being viewed by others
Introduction
Energy efficiency has become the most important metric of advancement in modern computer design1,2. One of the most well-known theories regarding the fundamental energy limits in computation is Landauer's principle3, where Rolf Landauer predicted that the erasure of 1-bit information generates heat of more than kBTln2, so that the entropy of the system does not decrease, where kB is the Boltzmann constant and T is temperature. This principle imposed the Landauer bound of kBTln2 as the minimum energy dissipation on irreversible logic operations, such as AND and OR, because they erase 1-bit information at every logic operation. After long discussions and numerical analyses of this energy bound4,5,6, some very recent experimental demonstrations that confirmed its validity have been reported7,8. These results indicate that the Landauer bound limits the minimum energy dissipation in modern CMOS-based computers9,10,11,12, which perform irreversible logic operations. In order to go beyond this bound, Edward Fredkin established a theory of reversible computing13, where the entropy of information is conserved during computation to prevent the heat generation resulting from the entropy reduction. He introduced the Fredkin gate13 as a 3-in/3-out reversible logic gate, which is logically reversible14 because its inputs are uniquely determined from its outputs, thereby conserving the entropy during computation. As part of the effort to achieve practical reversible logic gates, several physical models and devices have been proposed15,16,17,18. However, no reversible logic operations have been experimentally demonstrated to date. Thus, discussions on reversible computing remain theoretical and the question as to whether reversible computing is achievable using practical logic devices has yet to be resolved.
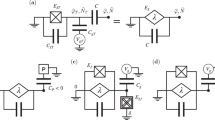
In order to achieve reversible logic gates, an extremely energy-efficient logic device is first necessary because the energy dissipated by the erasure of information is of the order of kBT. The bit energy of conventional logic devices, including CMOS and energy-efficient superconductor logics19,20,21, is at least larger than ~1,000kBT, which is too large to permit their use as reversible logic gates. In contrast, the adiabatic quantum-flux-parametron (AQFP) logic22,23,24,25, which is an adiabatic superconducting logic device, is a good candidate for use as a building block of reversible logic gates because its bit energy can go below kBT due to adiabatic switching operations25. Figure 1a shows the equivalent circuit of an AQFP buffer/NOT gate, which is based on the quantum-flux-parametron (QFP) gate invented by Eiichi Goto26,27. The gate is composed of inductances, L1, L2 and Lq along with the Josephson junctions, J1 and J2. By applying magnetic fluxes to the gate using an ac excitation current, Ix, either J1 or J2 will switch depending on the direction of the input current, Iin. As a result, one single-flux-quantum (SFQ) is stored in the loop composed of either L1, Lq and J1 or L2, Lq and J2, generating an output current, Iout through a mutual inductance, M = kio(LqLout)0.5. During this switching event, the potential energy of the gate changes adiabatically or reversibly from a single-well to a double-well, without a sudden state transition22,23. This means that the switching energy can be much smaller than the energy barrier height, IcΦ0, which corresponds to energy dissipation during a non-adiabatic 2π-transition in a current-biased Josephson junction, where Ic is a critical current of Josephson junctions and Φ0 is an SFQ.
Circuit schematics of AQFP and RQFP gates.
(a) AQFP buffer/NOT gate. The direction of Iout defines the logic state of the output port, x; the state is “1” for Iout > 0 and “0” for Iout < 0. For kio > 0, the directions of Iin and Iout are the same. Therefore this gate operates as a buffer gate. For kio < 0, Iin and Iout are in the opposite directions and the gate operates as a NOT gate. The circuit parameters were optimized in the previous work23 as φx/2π = 0.5, βL = 0.2 and βq = 1.6, where φx = 2πMIx/Φ0, βL = 2πLIc/Φ0, βq = 2πLqIc/Φ0, L = L1 = L2, Lx = Lx1 = Lx2, k = k1 = k2 and M = k(LLx)0.5. The critical current, Ic is 50 μA. (b) AQFP 3-in MAJ gate. White blocks correspond to AQFP buffer gates. The state of a MAJ gate is determined by the sum of the three input currents, Iina, Iinb and Iinc. Therefore, the state of the output (x) is determined to be x = MAJ(a, b, c). (c) AQFP 3-out SPL gate, whose circuit topology is the same as that of a 3-in MAJ gate. The input current, Iina, is shared by the three buffer gates in a SPL gate and the states of the outputs (x, y and z) are determined to be x = y = z = a. (d) RQFP gate, which is logically and physically reversible. The circuit topology of the RQFP gate is symmetrical, because those of a 3-in MAJ gate and a 3-out SPL gate are the same.
Results and Discussion
A logic gate is considered to be physically reversible28 if its potential energy changes adiabatically and reversibly. Konstantin K. Likharev argued that physical reversibility is necessary to prevent non-adiabatic energy dissipation during a switching event28, as well as logical reversibility. Bit information in a physically reversible gate can propagate bi-directionally, therefore the circuit topology of a reversible logic gate must be symmetrical in the data flow direction. In this study, we utilize 3-in majority (MAJ) gates and 3-out splitter (SPL) gates as building blocks. Figure 1b shows a block diagram of a 3-in MAJ gate with three input buffers, where a white block corresponds to an AQFP buffer gate. The logic state of the output port, x, is defined as x = MAJ(a, b, c) = a·b + b·c + c·a, where a, b, c are the logic states of the three input ports. Figure 1c is the block diagram of a 3-out SPL gate with an input buffer. The logic states of each output port are determined to be x = y = z = a. While the 3-in MAJ gate and the 3-out SPL gate have the same circuit topologies, the data flow direction, or the order of the excitation of each gate, is opposite. Figure 1d shows a block diagram of our proposed 3-in and 3-out reversible logic gate, which we have designated as the reversible quantum-flux-parametron (RQFP) gate. The RQFP gate is composed of three 3-in MAJ gates and three 3-out SPL gates, whose function is represented by the following equation:

Table I is the truth table of the RQFP gate. This table clearly shows that the gate is injective and logically reversible by operating the function two times: F(F(a, b, c)) = (a, b, c). Additionally, the RQFP gate is considered to be a primitive gate in reversible computing, because MAJ, NOT gates and constant inputs constitute a logical primitive. Because a 3-in MAJ gate and a 3-out SPL gate have the same circuit topologies, the topology of the RQFP gate is symmetrical. Data in the RQFP gate can propagate bi-directionally due to this symmetrical circuit topology, depending on the order of excitation. Specifically, if the SPL gates are excited earlier (excitation current, Ix1 is provided earlier than Ix2), the data propagates from the ports, a, b and c to x, y and z. If the MAJ gates are excited earlier, the data propagates in the opposite direction. Therefore, the RQFP gate is physically reversible.
To demonstrate logical and physical reversibility of an RQFP gate, we conducted three kinds of experiments, α, β and γ. The block diagrams of these three experiments are shown in Fig. 2a, where a, b and c are input ports and x, y and z are output ports. In the experiment α, we demonstrate logic operations of an RQFP gate. In β, two RQFP gates are serially connected to demonstrate logical reversibility. Specifically, if a = a’, b = b’ and c = c’, the RQFP gate is injective and proven to be logically reversible. In γ, two RQFP gates are connected but one is physically mirrored to demonstrate physical reversibility. Specifically, if a = a”, b = b” and c = c”, data can propagate bi-directionally in an RQFP gate and the gate is proven to be physically reversible. The RQFP gates were designed and fabricated using the Nb Josephson process, the AIST standard process (STP2)29. Figure 2b is a microphotograph of the circuits used in experiment γ, where Ix1, Ix2 and Ix3 are three-phase excitation currents. Here, it can be seen that two RQFP gates are serially connected but their physical layouts are horizontally mirrored. Figure 2c shows the measurement results of the experiments α, β and γ, using trapezoidal excitation currents of 100 kHz at 4.2K. In the experiment α, the correct logic operations were confirmed for the RQFP gate. In β, the obtained outputs (a’, b’ and c’) corresponded to the inputs (a, b and c), which proves the logical reversibility of the RQFP gate. Similarly, the outputs corresponded to the inputs in γ, which proves its physical reversibility. These results confirm that the RQFP gate is logically and physically reversible and that the RQFP gate is a practical reversible logic gate.
Demonstration of logical and physical reversibility of the RQFP gate.
(a) Block diagrams for experiments α, β and γ. In α, three inputs (a, b and c) are externally applied and three outputs (x, y and z) are observed to confirm its logic operations. In β, two RQFP gates are serially connected to determine if the gate is injective. In γ, two RQFP gates are serially connected but one is mirrored to determine if data can propagate bi-directionally. (b) Micrograph of circuits for the experiment γ. Dc superconducting quantum interference devices (dc-SQUIDs) were used for readout of output ports (a”, b” and c”), which detect output currents of buffer gates. One of the two RQFP gates is physically mirrored. (c) Measurement results, which were conducted at 4.2 K in liquid He. We used three-phase trapezoidal excitation currents of 100 kHz (Ix1, Ix2 and Ix3). Input currents (a, b and c) were given by using a data-pattern generator. Output voltages were amplified by differential amplifiers.
Next, we calculated energy dissipation of the RQFP gate by integrating the product of excitation currents and voltages over time using the Josephson circuit simulator, JSIM30. Figure 3a shows a block diagram for the simulation, where input and output buffers are inserted to avoid the interaction with input and output ports. Figure 3b provides the simulation results and shows the total energy dissipation per clock cycle, including an RQFP gate, input and output buffers, as a function of a rise/fall time of excitation currents. As can be seen in the figure, energy dissipation decreases almost linearly with an increase in the rise/fall time for all input patterns, which indicates that all gates operate adiabatically and reversibly during logic operations25,28. For a rise/fall time of 10,000 ps, the total energy dissipation of the RQFP gate and buffers composed of 69 AQFP gates reaches ~ 1 × 10−21 J/cycle. The bit energy per AQFP gate is ~ 2 × 10−23 J/cycle, which is much smaller than the barrier height, IcΦ0 ~ 1.0 × 10−19 J for Ic = 50 μA and around the same order of magnitude as the Landauer bound at 4.2 K, kBTln2 ~ 4.0 × 10−23 J. These calculation results show that there is no minimum energy dissipation for reversible logic operations using the RQFP gates.
Energy dissipation of the RQFP gate.
(a) Block diagram for simulation. Input and output buffers were inserted to avoid interaction with input and output ports. (b) Simulated energy dissipation, including an RQFP gate, input and output buffers. It was assumed that Lout = Lq and kio = 0.1 for AQFP buffer gates and that each wiring inductance is 10 pH for 3-in MAJ gates and 3-out SPL gates. For all input patterns, energy dissipation decreases almost linearly with an increase of a rise/fall time of excitation currents, which indicates that there is no minimum energy dissipation for reversible logic operations using RQFP gates (see Supplementary Information for energy dissipation of irreversible logic gates). The inset shows the definition of an excitation current.
Conclusions
Based on the above results, we can conclude that the RQFP gate is the first practical reversible logic gate. It is clear that through the use of RQFP gates, detailed discussion and investigations on the energy efficiency of reversible computing will become possible. Although the energy dissipation of the RQFP gate was too small to measure in the low-speed demonstration at 100 kHz, we expect that we will be able to measure it at a higher operation frequency (~1 GHz) in future work by using high-speed interface circuits31 and the superconducting resonator-based method24. Also, in previous work24, we have confirmed that calculation results of energy dissipation well agree with experimental results using superconducting resonators.
References
Ball, P. Computer engineering: Feeling the heat. Nature 492, 174–6 (2012).
Service, R. F. Computer science. What it'll take to go exascale. Science 335, 394–6 (2012).
Landauer, R. Irreversibility and Heat Generation in the Computing Process. IBM J. Res. Develop. 5, 183–191 (1961).
Shizume, K. Heat generation required by information erasure. Phys. Rev. E 52, 3495–3499 (1995).
Dillenschneider, R. & Lutz, E. Memory Erasure in Small Systems. Phys. Rev. Lett. 102, 1–4 (2009).
Sagawa, T. & Ueda, M. Minimal Energy Cost for Thermodynamic Information Processing: Measurement and Information Erasure. Phys. Rev. Lett. 102, 250602 (2009).
Bérut, A. et al. Experimental verification of Landauer's principle linking information and thermodynamics. Nature 483, 187–9 (2012).
Orlov, A. O., Lent, C. S., Thorpe, C. C., Boechler, G. P. & Snider, G. L. Experimental Test of Landauer's Principle at the Sub-kBT Level. Jpn. J. Appl. Phys. 51, 06FE10 (2012).
Keyes, R. W. Fundamental limits in digital information processing. Proc. IEEE 69, 267–278 (1981).
Lloyd, S. Ultimate physical limits to computation. Nature 406, 1047–54 (2000).
Meindl, J. D. & Davis, J. A. The fundamental limit on binary switching energy for terascale integration (TSI). IEEE J. Solid-St. Circ. 35, 1515–1516 (2000).
Zhirnov, V. V., Cavin, R. K., Hutchby, J. A. & Bourianoff, G. I. Limits to binary logic switch scaling-a gedanken model. Proc. IEEE 9, 1934–1939 (2003).
Fredkin, E. & Toffoli, T. Conservative logic. Int. J. Theor. Phys. 21, 219–253 (1982).
Bennett, C. H. Logical Reversibility of Computation. IBM J. Res. Develop. 17, 525–532 (1973).
Keyes, R. W. & Landauer, R. Minimal Energy Dissipation in Logic. IBM J. Res. Develop. 14, 152–157 (1970).
Likharev, K. Dynamics of some single flux quantum devices: I. Parametric quantron. IEEE Trans. Magn. 13, 242–244 (1977).
Semenov, V. K., Danilov, G. V. & Averin, D. V. Negative-inductance SQUID as the basic element of reversible Josephson-junction circuits. IEEE Trans. Appl. Supercond. 13, 938–943 (2003).
Ren, J. & Semenov, V. K. Progress With Physically and Logically Reversible Superconducting Digital Circuits. IEEE Trans. Appl. Supercond. 21, 780–786 (2011).
Herr, Q. P., Herr, A. Y., Oberg, O. T. & Ioannidis, A. G. Ultra-low-power superconductor logic. J. Appl. Phys. 109, 103903 (2011).
Mukhanov, O. A. Energy-Efficient Single Flux Quantum Technology. IEEE Trans. Appl. Supercond. 21, 760–769 (2011).
Tanaka, M., Ito, M., Kitayama, A., Kouketsu, T. & Fujimaki, A. 18-GHz, 4.0-aJ/bit Operation of Ultra-Low-Energy Rapid Single-Flux-Quantum Shift Registers. Jpn. J. Appl. Phys. 51, 053102 (2012).
Takeuchi, N., Ozawa, D., Yamanashi, Y. & Yoshikawa, N. An adiabatic quantum flux parametron as an ultra-low-power logic device. Supercond. Sci. Tech. 26, 035010 (2013).
Takeuchi, N., Ehara, K., Inoue, K., Yamanashi, Y. & Yoshikawa, N. Margin and Energy Dissipation of Adiabatic Quantum-Flux-Parametron Logic at Finite Temperature. IEEE Trans. Appl. Supercond. 23, 1700304 (2013).
Takeuchi, N., Yamanashi, Y. & Yoshikawa, N. Measurement of 10 zJ energy dissipation of adiabatic quantum-flux-parametron logic using a superconducting resonator. Appl. Phys. Lett. 102, 052602 (2013).
Takeuchi, N., Yamanashi, Y. & Yoshikawa, N. Simulation of sub-kBT bit-energy operation of adiabatic quantum-flux-parametron logic with low bit-error-rate. Appl. Phys. Lett. 103, 062602 (2013).
Harada, Y. et al. Basic operations of the quantum flux parametron. IEEE Trans. Magn. 23, 3801–3807 (1987).
Hosoya, M. et al. Quantum flux parametron: a single quantum flux device for Josephson supercomputer. IEEE Trans. Appl. Supercond. 1, 77–89 (1991).
Likharev, K. K. Classical and quantum limitations on energy consumption in computation. Int. J. Theor. Phys. 21, 311–326 (1982).
Nagasawa, S., Hashimoto, Y., Numata, H. & Tahara, S. A 380 ps, 9.5 mW Josephson 4-Kbit RAM operated at a high bit yield. IEEE Trans. Appl. Supercond. 5, 2447–2452 (1995).
Whiteley, S. R. Josephson junctions in SPICE3. IEEE Trans. Magn. 27, 2902–2905 (1991).
Takeuchi, N., Ortlepp, T., Yamanashi, Y. & Yoshikawa, N. High-Speed Experimental Demonstration of Adiabatic Quantum-Flux-Parametron Gates Using Quantum-Flux-Latches. IEEE Trans. Appl. Supercond. 24, 1300204 (2014).
Acknowledgements
This work was supported by a Grant-in-Aid for Scientific Research (S) (No. 22226009) from the Japan Society for the Promotion of Science (JSPS). The circuits were fabricated in the clean room for analog-digital superconductivity (CRAVITY) of National Institute of Advanced Industrial Science and Technology (AIST) with the standard process 2 (STP2). The AIST-STP2 is based on the Nb circuit fabrication process developed in International Superconductivity Technology Center (ISTEC). We would like to thank C. J. Fourie for improving the 3D inductance extractor, InductEx that we used during the layout design of the circuits.
Author information
Authors and Affiliations
Contributions
N.T. designed circuits, carried out simulations and experiments and wrote the paper. Y.Y. and N.Y. supported theoretical aspects and supervised simulations and experiments. All authors discussed the results and commented on the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Energy dissipation of irreversible logic gates
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Takeuchi, N., Yamanashi, Y. & Yoshikawa, N. Reversible logic gate using adiabatic superconducting devices. Sci Rep 4, 6354 (2014). https://doi.org/10.1038/srep06354
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep06354
This article is cited by
-
Reversibility and energy dissipation in adiabatic superconductor logic
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.