Introduction

Driven diffusive system is a rewarding research topic in recent decades, which exhibits non-vanishing current even in the steady state and has served as fruitful testing grounds for fundamental research in non-equilibrium physics1,2,3,4,5. The driven diffusive systems exhibit many surprising or counterintuitive features, given our experiences with equilibrium systems, e.g., spontaneous symmetry breaking, phase separation, etc.6,7,8,9,10.

The boundary induced phase transition is another non-equilibrium phenomenon11,12,13,14. For the case of vanishing right boundary density, Krug postulated a rather general maximal-current principle that the system tries to maximize its stationary current11. The maximal-current principle has later been generalized to the extremal current principle12,13

Here ρ−(ρ+) is the constant effective density of the left (right) reservoir from which particles are flowing into (out of) the system and ρ is system density, which is defined as the occupancy probability of sites. The microscopic details of the system only determine the functional form of the current q(ρ) and the effective boundary densities.

Motivated by facts such as the unidirectional motion of many motor proteins along cytoskeletal filaments, in which motors advance along the filament while attachment and detachment of motors between the cytoplasm and the filament occur, the constraint of the conserved dynamics in the bulk in the driven diffusive system has been relaxed to consider random particle attachments and detachments in the bulk15. The resulting dynamics leads to a phase coexistence of low and high density regions separated by a shock.

The driven diffusive systems have also been extended to include the possibility of transport on multiple parallel lanes to describe phenomena such as the extraction of membrane tubes by molecular motors, macroscopic clustering phenomena, car traffic and so on (see e.g. Refs. [16,17,18,19,20,21,22,23,24,25,26,27,28,29] and references therein), in which the boundary induced phase transitions still could be observed.

This paper studies a weakly and asymmetrically coupled three-lane totally asymmetric simple exclusion process (TASEP) and reports a bulk induced phase transition. Our model is defined in a three-lane lattice of N×3 sites, where N is the length of a lane (see Fig. 1). For each time step, a site is chosen at random. A particle at site i and lane j can jump with rate 1 to site i + 1 if it is unoccupied. Otherwise, if site i + 1 is occupied, the particle jumps to site i on lane j + 1 with rate ωA and to site i on lane j−1 with rate ωB (ωB≠ωA), provided the target site is unoccupied. Obviously, ωB = 0 for lane 1 and ωA = 0 for lane 3. We use this rule to mimic the feature of cars, since cars usually will not change lane when unhindered. The model was also stimulated by fast and strong motor proteins, like kinesins, which do not change lines frequently. However, these details do not change the physics of the observed phenomena. Without this rule (i.e., a particle can change lanes provided the target site is empty) the system dynamics do not qualitatively change.

Figure 1
figure 1

Sketch of the three-lane TASEP.

The arrow shows allowed hopping and the cross shows prohibited hopping.

Full size image

The asymmetric coupling makes the middle lane different from two other lanes and bulk induced phase transition occurs on this lane. At the boundaries, a particle enters from the left boundary with rate α and is removed from the right boundary with rate β. As in previous studies, a weakly coupling is considered in which ωAN = ΩA and ωBN = ΩB are kept constant. We have studied the model using both mean-field calculation (see section Method) and Monte Carlo simulations.

Results

Figure 2 shows a typical phase diagram of a three-lane system, in which an asymmetrical set of parameters ΩA = 10 and ΩB = 0.1 is adopted. In the phase diagram, XYZ stands for the state of the three lanes. L(H) means that the corresponding lane j is in low (high) density phase ρj<0.5 (ρj>0.5), S means that there is a shock on the lane (shocks S1 and S2 denote bulk induced shocks as discussed below), D means that there are two shocks on the lane, C means that the density profile is a continuously and smoothly decreasing one and crosses the density ρ = 0.5. The transitions among LLL, LLS, LSS, LLH, LSH, LHH, SSH, SHH, HHH can be easily understood as boundary induced phase transitions, see e.g., Refs. [19,20]. For instance, when ρ3(1), the density at the right end on lane 3, increases to min (β, 1/2) in the LLL phase, a shock is induced from the right boundary on this lane and thus the LLL phase transits into LLS phase. Fig. 3 shows the typical density profiles of these states.

Figure 2
figure 2

Phase diagram of the three-lane TASEP obtained from mean-field calculation.

The parameters ΩA = 10and ΩB = 0.1. Details about the dotted lines and the dashed lines 1–5 are in the text.

Full size image
Figure 3
figure 3

Typical density profiles.

(a) LLL, (b) LLS, (c) LSS, (d) LLH, (e) LSH, (f) LHH, (g) SSH, (h) SHH, (i) HHH. The scatter data are simulation results and the dashed lines are mean field results. (α, β) = (0.1, 0.25), (0.1, 0.15), (0.074, 0.087), (0.268, 0.286), (0.2, 0.18), (0.278, 0.166), (0.15, 0.098), (0.45, 0.11), (0.45, 0.09) in (a) – (i), respectively. In the simulation, the system size N = 20000.

Full size image

We focus on the density profiles in the LLS state. Fig. 4(a) shows several typical density profiles with the fixed value β = 0.276. Note that in the LLS state, due to existence of a shock on the third lane, the density profile is not smooth in the middle lane at the shock location, which separates the density profile into two parts. When α is left to the dotted line in the phase diagram, the density profile in the downstream part is increasing with x. With the increase of α, the shock moves left, so that the downstream part expands. Across the dotted line, the density profile in the downstream part becomes non-monotonically changing. This is because (J1→2 + J3→2)−(J2→1 + J2→3) begins to change sign with x in the downstream part. Here Jk→j means flow from lane k to lane j. In the LLH state, the shock has been expelled out from the left end and the density profile is always monotonically changing. On the boundary between LLH and LS1H, the extreme value of the density profile on lane 2 reached ρ = 0.5. As a result, a bulk induced phase transition occurs, which exhibits a shock (S1) as well as a continuous and smooth density profile that crosses ρ = 0.5 downstream of the shock. Note that when ρ2 = 0.5, the coefficient (1–2ρ2) in eq.(11) equals zero. Consequently, the mean field equations (10)– (12) cannot be used to solve the density profile in the vicinity of ρ2 = 0.5, because the numerical solution diverges. We have used equations (7)– (9) instead.

Figure 4
figure 4

The density profiles of the middle lane (mean-field results).

(a) System transits from LLS to LS1H. Parameters are β = 0.276, α = 0.14, 0.15, 0.163, 0.17, 0.229, 0.29, 0.308 for curves from bottom to top. (b) System transits from SHH to LS2H. Parameters are α = 0.31, β = 0.088, 0.098, 0.108, 0.128, 0.152, 0.189, 0.206 for curves from top to bottom.

Full size image

Similarly, in the SHH state, the density profile located in the upstream part of the middle lane gradually becomes non-monotonically changing when (α, β) approaches the corresponding dotted line. Across the boundary between LHH and LS2H, a bulk induced shock (S2) as well as a continuous and smooth density profile that crosses ρ = 0.5 upstream of the shock appears, see Fig. 4(b).

Here we call “bulk induced” phase transition because the shock emerges in the bulk. Note that there is another viewpoint, in which lanes 1 and 3 are regarded as heterogeneous reservoirs for lane 2. Since the heterogeneity on lanes 1 and 3 comes from boundaries and thus the phase transitions are regarded as intrinsically induced by boundaries.

We study the density profiles in the LS1H state. Fig. 5(a) shows several density profiles with β = 0.296 is fixed. With the increase of α, the shock gradually moves left. Across the boundary between LS1H and LCH, the shock is expelled out from the left end and only the continuous and smooth density profile is left in the middle lane. Similarly, the shock is expelled out from the right end in the LS2H phase when across the boundary between LS2H and LCH, see Fig. 5(b).

Figure 5
figure 5

The density profiles of the middle lane (mean-field results).

(a) System transits from LS1H to LCH. The parameter β = 0.296. (b) System transits from LS2H to LCH. The parameter α = 0.358.

Full size image

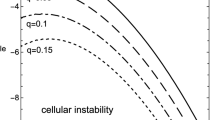
Figs. 6 (a) and (b) show the density profiles in the LSH phase, in which (α, β) changes along dashed lines 1 and 2 in the phase diagram, respectively. When (α, β) is left of the dotted line, the density profile is increasing both upstream and downstream of the shock. However, when across the dotted line, the density profile becomes non-monotonic upstream (downstream) of the shock. On the boundary between LSH and LDH, the maximum (minimum) of density profile reaches ρ = 0.5. When across the boundary, the bulk induced shock appears upstream (downstream) of the first shock and thus two shocks exist simultaneously in the middle lane.

Figure 6
figure 6

The density profiles of the middle lane (mean-field results).

(a) shows the transition from LSH to LDH along dashed line 1. Parameters are (α, β) = (0.154, 0.173), (0.178, 0.180), (0.190, 0.184), (0.211, 0.190), (0.241, 0.198) and (0.268, 0.206) for curves from bottom to top at x = 0. (b) shows the transition along dashed line 2. Parameters are (α, β) = (0.182, 0.128), (0.200, 0.145), (0.218, 0.161), (0.234, 0.175) and (0.268, 0.206) for curves from top to bottom at x = 1. (c) shows the transition from LS1H to LDH along dashed line 3. The parameter α = 0.305. (d) shows the transition from LS2H to LDH along dashed line 4. The parameter α = 0.318.

Full size image

Figs. 6(c) and (d) show the density profiles in the LS1H and LS2H phase, in which (α, β) changes along dashed lines 3 and 4, respectively. On approaching the boundary between LS1H (LS2H) and LDH, ρ2(1) (ρ2(0)) gradually approaches β ((1−α)). Across the boundary, a shock is induced from the right (left) boundary, thus, double shocks emerge.

Finally, in the LDH phase, when (α, β) changes along dashed line 5, the left shock moves toward left and the right shock moves right. On the boundary between the LDH phase and the LCH phase, the two shocks are expelled from the system, simultaneously, see Fig. 7.

Figure 7
figure 7

The density profiles of the middle lane (mean-field results).

System transits from LDH state to LCH state along dashed line 5.

Full size image

Discussion

Now we interpret why only one bulk induced shock is triggered. Suppose there are two bulk induced shocks. As a result, the density profile crosses ρ = 0.5 twice, i.e., there are two locations x1 and x2 (x1<x2) at which ρ2 = 0.5. Note that for the double shocks in the LDH state, the density profile crosses ρ = 0.5 only once. Thus, the double shocks can exist.

Now, we have the following equation at the two locations according to the current conservation principle

where 0 ≤ c ≤ 0.5 stands for a constant. Substituting ρ2 = 0.5 into eq.(11), we have

at locations x1 and x2. Suppose ΩA>ΩB, then one has ρ1<0.5 and ρ3>0.5 at the two locations. Thus, from eq.(2), ρ3 can be solved

Substituting eq.(4) into (3), one has

Taking derivative to ρ1, we obtain

where . Since ρ1<0.5, is always satisfied. This means that eq.(5) has at most one solution. Therefore, ρ1(x1) = ρ1(x2) and ρ3(x1) = ρ3(x2). When one lane-changing parameter equals 0, both ρ1(x) and ρ3(x) are monotonically changing with x. Therefore, ρ1(x1) = ρ1(x2) and ρ3(x1) = ρ3(x2) cannot be satisfied.

In the general situation that neither ΩA nor ΩB equals to 0, the section x ≤ x1 and the section x ≥ x2 can match each other and constitute a shortened system with length 1−(x2−x1), in which only one bulk induced shock exists. The mean-field analysis has shown that given the same values of α and β, the flow rate in a shortened system is larger than that in the original system, provided there exists one bulk induced shock in both systems. Thus, we argue that the current minimization principle excludes the occurrence of two or more bulk induced shocks.

Hinsch and Frey have studied a periodic one-dimensional exclusion process composed of a driven and a diffusive part and identified bulk-driven phase transitions in a mesoscopic limit where both dynamics compete30. Nevertheless, the system can be regarded as two sub-systems connecting together. Therefore, the bulk-driven phase transitions are essentially boundary induced ones.

In our system, we can also treat the location where the density profile crosses ρ = 0.5 as a virtual boundary, which separates the system into two sub-systems. For the left sub-system, the effective exit rate for the middle lane is β2,eff = 0.5. For the right one, the effective entrance rate for the middle lane is α2,eff = 0.5. Nevertheless, instead of a static boundary, the location of the virtual boundary in our system is self-tuned and determined by the values of the kinetic rates.

We also would like to point out that the existence of double shocks has been demonstrated when considering detachment and attachment of particles in the Katz-Lebowitz-Spohn process31. However, different from the double shocks in LDH state in our model, both shocks are boundary induced ones in Ref. [31].

Also note that, as pointed out in Ref. [16], when the minima of the current can be realized by several different densities simultaneously, multiple shocks can be observed, which separate the density profile into several flat segments with different densities corresponding to the minima. Nevertheless, the multiple shocks always emerge and disappear simultaneously. This is different from the double shocks in the present paper.

This paper only focuses on the three-lane TASEP. When the number of lanes further increases, the phase diagram will become much more complicated. The questions such as whether two or more bulk induced shocks could be observed simultaneously in a lane, whether bulk induced shocks can be observed simultaneously in different lanes, need to be investigated in the future work.

Methods

The hydrodynamic mean field equations of the system could be written as

In the steady state, one has

Here ρj denotes the density on lane j. Via rescaling the total length to unity (i.e., x = i/L), the boundary conditions ρj(0) = min (α, 1/2) and ρj(1) = max (1−β, 1/2) should be imposed properly, depending on the specific state of the system. Via numerical solving equations (10) – (12) and/or equations (7) – (9), we can obtain the density profiles of the three lanes. Specifically,

In the LLL phase, one has ρj(0) = min(α,1/2) (j = 1,2,3). Thus the density profiles of the three lanes can be obtained by numerical solving equations (10) – (12) from x = 0 to x = 1.

In the HHH phase, one has ρj(1) = max (1−β, 1/2) (j = 1,2,3). Thus the density profiles of the three lanes can be obtained by numerical solving equations (10) – (12) from x = 1 to x = 0.

In the LLS phase, one still has ρj(0) = min (α, 1/2). In this case, one needs to assume the location of the shock on lane 3, denoted as xs. Then one numerically solves equations (10) – (12) from x = 0 to x = xs. Denote the density on lane 3 at x = xs as ρ3(xs). One needs to change the density on lane 3 from ρ3(xs) to 1−ρ3(xs) and then continues to numerically solve equations (10) – (12) from x = xs to x = 1. If the choice of xs is correct, then one would have ρ3(1) = max (1−β, 1/2).

Similarly, in the LSS phase, one still has ρj(0) = min (α, 1/2) and needs to assume the locations of the shocks on both lanes 2 and 3 to match ρ2(1) = ρ3 (1) = max (1−β, 1/2).

In the LLH phase, one has ρ1(0) = ρ2(0) = min (α, 1/2) and needs to assume the value of ρ3(0) to match ρ3(1) = max (1−β, 1/2).

In the LSH phase, one has ρ1(0) = ρ2(0) = min (α, 1/2) and needs to assume the location of the shock on lane 2 and the value of ρ3(0) to match ρ2(1) = ρ3(1) = max (1−β, 1/2).

In the SHH phase, one has ρj(1) = max(1−β, 1/2) and needs to assume the location of the shock on lane 1 to match ρ1(0) = min(α, 1/2).

In the SSH phase, one still has ρj(1) = max(1−β, 1/2) and needs to assume the locations of the shocks on both lanes 1 and 2 to match ρ1(0) = ρ2(0) = min (α, 1/2).

In the LHH phase, one has ρ2(1) = ρ3(1) = max (1−β, 1/2) and needs to assume the value of ρ1(1) to match ρ1(0) = min (α, 1/2).

In the LCH phase, one has ρ1(0) = min (α, 1/2) and needs to assume the values of ρ2(0) and ρ3(0) to match ρ3(1) = max (1−β, 1/2). Note that the solution is not unique. Due to current minimization principle, the solution corresponding to the minimum current is the correct one.

In the LDH phase, one has ρ1(0) = ρ2(0) = min (α, 1/2) and needs to assume the two locations of the double shocks on lane 2 and the value of ρ3(0) to match ρ2(1) = ρ3(1) = max (1−β, 1/2). Still the solution is not unique and the current minimization principle determines the correct one.