Introduction

The bilayer honeycomb lattice (BHL) has attracted enormous interest in both experimental and theoretical research. Lots of novel phenomena have been found in BHL, for instance, the quantum Hall effect, quantum spin Hall effect and chiral superconductivity1,2,3,4,5,6,7,8,9,10,11. However, the real charge and magnetic order induced by Coulomb interaction are still challenges in the strongly correlated BHL12,13,14,15,16. A quadratic dispersion relation, signed by two touching bands in the corners of Brillouin zone, can be found in BHL, which is driven by the inter-layer hopping. In addition, the spontaneous symmetry can be broken by the dimers when the inter-layer hopping changes. Some amazing phases may emerge, such as layer anti-ferromagnetic phase and paramagnetic insulator phase. Previous work mainly focus on the electronic properties of BHL17,18,19,20,21,22,23,24 and the phase diagram for the magnetic phase transition induced by the interaction and dimers are still absent. Moreover, the progress of optical lattice provides us a useful tool to set a controllable and clearness experimental platform to simulate the strongly correlated BHL, in which the interaction between trapped fermionic cold atoms can be tuned by the Feshbach resonance25,26,27,28,29,30,31.

The dynamical mean-field theory (DMFT) has been proved to be a very useful and effective tool32,33,34,35, which has made significantly progress as in the study of metal-insulator phase transition. The DMFT is exact when investigating the strongly correlated system in the infinite-dimension, in which the self-energy is independent of momentum. However, in low-dimensional systems, the quantum fluctuation and short range correlations play important roles, which are ignored in DMFT. The cellular DMFT (CDMFT), as a cluster extension of DMFT, effectually incorporates the spatial correlations by mapping the many-body problem into finite clusters embedding in a self-consistent media36,37,38,39. In two-dimensional systems CDMFT is more precise than DMFT and is more effective to investigate the phase transition in low and multi-component systems31,40,41.

In this report, we investigate the finite temperature metal-insulator and magnetic phase transition in strongly correlated bilayer honeycomb lattice (BHL) by combining the cellular dynamical mean-field theory (CDMFT) with continue-time quantum Monte Carlo (CTQMC) method42. A phase transition from paramagnetic phase to anti-ferromagnetic phase occurs by investigating the magnetization. In a proper value of inter-layer hopping, a novel layer anti-ferromagnetic phase emerges. The layer anti-ferromagnetic phase can be broken by the increasing inter-layer hopping and a paramagnetic phase can be found. Moreover, the nonlocal inter-layer hopping plays an important role on localizing the free election and modifying the spatial distribution of the electron in lattice sites, especially in dimer sites. For instance, the dimer sites of our system are double occupied and the non-dimer sites are single occupied. We have also presented the DOS, double occupancy and fermi surface below, which can be directly detected in future experiments.

Results

The strongly correlated bilayer honeycomb lattice

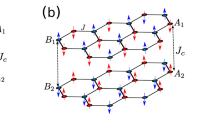
Fig. 1(a) shows the lattice structure of BHL. A1 and B1 denotes the sites on top-layer, while A2, B2 signs the bottom-layer sites. The inter-layer band connects A1 (top) and A2 (bottom) sites. The first Brillouin zone can be found in Fig. 1(c), in which the Γ, K, M and K′ shows the points with different asymmetry in the k-space. The non-interaction density of states (DOS) for different sites when t1 = t is shown in Fig. 1(d), which is different from the mono-layer honeycomb lattice43. The low-energy dispersion is quadratic, which is linear in the mono-layer case. There is no band gap between the conduction and valence bands in BHL. In this report, we investigate the phase transition on the half-filling BHL. We consider the standard Hubbard model:

where t is the intra-layer nearest-neighbor hopping energy, U is the Coulomb interaction, t1 denotes the inter-layer hopping energy, µ is the chemical potential, which is adjusted to keep the system at half-filling, and ciσα denote the creation and annihilation operators of fermionic atoms on site i with spin σ respectively and α shows the layer parameter (α = 0 means the top-layer and α = 1 denotes the bottom-layer), corresponds to the density operator. Here we set t = 1, which is also used as the energy unit in this report.

Figure 1
figure 1

The structure of bilayer honeycomb lattice and its qualities in the non-interacting limit.

(a): Bernal stacking of the bilayer honeycomb in real-space with intra- and inter-layer hopping t and t1 between the sublattice A1, B1 on top-layer and A2, B2 on bottom-layer. The black arrows a1 and a2 are the lattice vectors. (b): The cellular of our bilayer system in cellular dynamical mean-field theory (CDMFT). The red solid line containing sites 0, 1, 2, 3, 4, 5 belongs to top-layer and blue dotted line with sites 6, 7, 8, 9, 10, 11 belongs to bottom-layer. (c): Reciprocal lattice of bilayer honeycomb lattice. The thick red line shows the first Brillouin zone. The Γ, K, M and K′ points denote high symmetry points in first Brillouin zone. (d): Density of states of our system for A1/A2 and B1/B2 sites when U = 0.

Full size image

The metal-insulator phase transition

The t1 − U phase diagram is shown in Fig. 2. The phase boundary of the metal and insulator is shown by the red solid line with square plots. When t1 = 0 the critical point of metal-insulator phase transition is Uc = 4.7, meaning that BHL degenerates into a mono-layer one. This result is the same as Ref. 16. In order to study the magnetic phase transition, we define the staggered magnetization as M = Σisgn(i)(< ni↑ > − < ni↓ >), where i denotes the lattice index, sgn(i) = 1 for A1 and A2 sites and sgn(i) = −1 for B1 and B2 sites. The phase boundary of non-magnetic state and magnetic state is shown by blue solid lines with circle points. As shown in Fig. 2, when 2 < t1 < 4.8, anti-ferromagnet can be found. When U is increased, a phase transition from gapless anti-ferromagnetic metal (AFM), where ΔE = 0, M ≠ 0 and ΔE here is single particle gap, to gapped anti-ferromagnetic insulator (AFI), where ΔE ≠ 0, M ≠ 0, occurs. When t1 < 2, a paramagnetic metal (PM), where ΔE = 0, M = 0, is formed and a PM-AFM-AFI transition happens when U is increased. In the value of 0 < t1 < 0.2, when U > 4.7, a small region, which is named as paramagnetic insulator (PI) is found with ΔE ≠ 0 and M = 0.

Figure 2
figure 2

Metal-insulator phase diagram in fixed T or t1.

Phase diagram as a function of inter-layer hopping t1 and interaction U at T = 0.1. The red solid line shows the boundary of metal-insulator phase transition and the blue solid line denotes the magnetic phase transition, which divides the phase into paramagnetic metal (PM: M = 0 and ΔE = 0), paramagnetic insulator (PI: M = 0 and ΔE ≠ 0), anti-ferromagnetic metal (AFM: M ≠ 0 and ΔE = 0) and anti-ferromagnetic insulator (AFI: M ≠ 0 and ΔE ≠ 0). Inset: Phase diagram as a function of temperature T and interaction U at fixed t1.

Full size image

Double occupancy is always used to measure the localization of the electrons directly, which is an important parameter to observe the metal-insulator phase transition44. In this report, we investigate the double occupancy as a function of inter-layer hopping t1 for various interaction U [see in Fig. 3], where F is the free energy. We use DAA to describe the Docc for A1 and A2 sites (hollow circles in Fig. 3) and DBB the Docc for B1 and B2 sites (solid circles in Fig. 3). When t1 = 0, Docc decrease when U is increased showing the localization is enforced by the interaction. When t1 ≠ t, DAA is different with DBB. It is found that when t1 is increased, DAA increases while DBB decreases. This suggests the itinerancy of electrons in dimer sites is enhanced due to the increasing inter-layer hopping. However, be different with DAA, DBB decreases while t1 is increased. These results suggest the intra-hopping between dimer and non-dimer sites is weaken due to the forming of spin-polarized electrons in dimer sites.

Figure 3
figure 3

The evolution of double occupancy Docc.

The double occupancy as a function of inter-layer hopping t1 for different interaction U at temperature T = 0.1. The dimer sites tend to be double occupied however non-dimer sites tend to be single occupied, with increasing t1.

Full size image

We derive DOS from the imaginary time Green's function G(τ) to observe the single particle spectral for different interaction U and t1 by the maximum entropy method45,46. Fig. 4(a) and Fig. 4(e) shows the DOS for different inter-layer hopping when U = 2.5, T = 0.1 for A sites and B sites. It is found that, in weak interaction, the inter-layer hopping t1 does not affect the metallic properties of BHL. In Fig. 4(b) and Fig. 4(f), we can find that the system keeps at a metallic state when t1 = 1.8 and an obvious pseudo-gap is found when t1 = 2.2. A metal-insulator transition happens when t1 = 3.2 for U = 3.5 and T = 0.1 for both A and B sites. When interaction being large, such as U = 6.0 [see Fig. 4(c) and Fig. 4(g)], the system stays at an insulating state, which is insensitive of t1. Fig. 4(d) and Fig. 4(h) show the DOS for different U when t1 = 1.0 and T = 0.1. An opened gap is found when the interaction is increased, which indicates a phase transition from metal to insulator. These results mean that the inter-layer hopping and Coulomb interaction play same roles for the metal-insulator phase transition.

Figure 4
figure 4

The density of states.

(a) – (c), (e) – (g): The density of states as a function of frequency ω for different inter-layer hopping t1 at temperature T = 0.1. (a), (e): The metallic phase at U = 2.5 for A sites and B sites. (b): For A sites, as we increase t1, system undergoes a phase transition from metal (at U = 3.5 and t1 = 1.8) to insulator (at t1 = 3.2). Single particle excitation gap opens at about t1 = 3.2. (f): For B sites, same tendency occurs and the critical point is also at about t1 = 3.2. (c), (g): The insulating phase at U = 6.0. There is a visible single particle excitation gap around the Fermi energy. (d), (h): The density of states as a function of ω for different U with fixed t1.

Full size image

In this report, the Fig. 5 shows the spectral function A(k, ω = 0) near the Fermi surface for various U and t1. A(k, ω) is defined as:

where iω is the Fermionic Matsubara frequency, denotes the dispersion relation, Σk(iω) corresponds to the k-dependent self-energy, k is the wave vector in the first Brillouin zone. Figs. 5(a)–(c) show the A(k, ω = 0) for different t1 when U = 3.5. When t1 < 3.2, we can find that the peaks of A(k, ω = 0) distribute in the K and K′ points [see Fig. 1(c)] in k-space, displaying a metallic behavior [see Figs. 5(a), (b)]. When t1 = 4.0, the A(k, ω = 0) ≈ 0 [see Fig. 5(c)], meaning that a gap can be found near the Fermi energy. This gapped behavior shows the system is an insulator. Similar behavior is found when t1 = 1.2 and U is increased [see Figs. 5(d) – (f)]. It means both spin-polarization and strongly correlated interaction can induce the localization of electrons, driving the system from metal to insulator.

Figure 5
figure 5

The evolution of spectral function near Fermi surface.

The spectral function A(k, ω = 0) near the Fermi surface for different inter-layer hopping t1 at T = 0.1 and U = 3.5: (a) t1 = 1.0, (b) t1 = 1.8, (c) t1 = 4.0. The A(k, ω = 0) when T = 0.1 and t1 = 1.2 for different interaction U: (d) U = 2.0, (e) U = 2.8, (f) U = 4.5.

Full size image

The magnetic phase transition and a novel layer anti-ferromagnetic phase

In strongly correlated BHL, charge imbalance between the two sublattices sites causes different kinds of magnetic spontaneous symmetry breaking, dividing the sites into dimer sites and non-dimer sites. In order to study the magnetic order, we use a magnetic order parameter defined as , where α denotes the sublattice A1, A2, B1 and B2, iα is the lattice index for sublattice α and Nα means the site number for sublattice α [see in Fig. 1(a) and Fig. 1(b)]. Parameter < niσ > indicates the electron density in lattice site i with spin index σ (we set magnetization of A1 as positive sign). Fig. 6 shows the evolution of mα as a function of t1 for U = 3.8. It is found that when U = 3.8, m is zero for t1 < 1.0, denoting that no magnetic order is formed for weak t1. A magnetic state with anti-ferromagnetic order is found when t1 > 1.0. When t1 > 4.4, the and decrease to zero, while , are still finite, meaning a phase with non-magnetic order and magnetic order coexisting. This novel phase is called layer anti-ferromagnetic state, in which the dimer sites are non-magnetic and non-dimer sites are magnetic. The sketches of the possible magnetic order existing in BHL is shown in Figs. 7(a) – (c).

Figure 6
figure 6

The evolution of the magnetic order parameter m.

The evolution of magnetic order parameter m at T = 0.1 and U = 3.8. A paramagnetic phase is found in weak t1. For t1 > 1.0, the magnetic parameter m is nonzero and has opposite sign between A1/A2 sites and B1/B2 sites. The system goes into anti-ferromagnetic phase. At large t1 the magnetization of A1/A2 sites are more easily decreasing to zero while B1/B2 sites are still nonzero. The system is layer anti-ferromagnetic phase. Single particle excitation gap ΔE denoted by the dark green solid line and orange solid line, divide the phase into paramagnetic metal (PM), anti-ferromagnetic metal (AFM), anti-ferromagnetic insulator (AFI) and layer anti-ferromagnetic insulator (LAFI).

Full size image
Figure 7
figure 7

The phase diagram of magnetic phase transition.

In weak interaction U and weak inter-layer hopping t1, the system is paramagnet. When we increase U, the system undergoes a magnetic phase transition to anti-ferromagnet. When we increase t1, the magnetization of A1/A2 sites decrease to zero while B1/B2 sites stay finite. The system becomes layer anti-ferromagnet. In the region where t1 > 5.0, the system returns to paramagnetic phase.

Full size image

Finally, the phase diagram of magnetization about t1 and U for T = 0.1 is shown in Fig. 7. A phase transition from paramagnet to anti-ferromagnet is found when U is increased. A layer anti-ferromagnetic phase is found for large t1, in which the magnetic of dimer sites keeps zero while non-dimer sites is nonzero. When U > 3.7, a phase transition from layer anti-ferromagnetic state to paramagnetic state is found.

Experimental protocol

We propose an experiment setup to investigate the phase transition in strongly correlated bilayer honeycomb lattice (BHL). The 40K atoms can be produced as a pure fermion condensate by evaporative cooling47, which provides two hyperfine states |F,mF〉 = |9/2, −9/2〉 ≡ | ↑〉 and |F,mF〉 = |9/2, −7/2〉 ≡ | ↑〉48. Three standing-wave laser beams are used to form the honeycomb lattice and two extra laser beams along the z direction suppress the tunneling between layers28. The potential of optical lattice is given by Vh(x, y) = V0Σj= 1,2,3sin2[k(x cos θj+y sin θj)+π/2], where θ1 = π/3, θ2 = 2π/3, θ3 = 0. Then, we use another three standing-wave laser beams with a 2π/3 angle between each other to form triangular lattice. The potential is given by . kx and ky are the two components of the wave vector k = 2π/λ in these two types of lattices, where λ = 738 nm is wavelength of the laser and V0 is given in recoil energy . Inserting the triangular lattice between two layers of honeycomb lattice, the Bernal stacking BHL with trapped 40K atoms can be formed49,50. In BHL the intra-layer hopping is adjusted by the periodic potential of laser beam and t1 can be tuned by changing the wavelength of laser beam in z direction. The on-site interaction is determined by the s-wave scattering length as, which can be tuned by Feshbach resonance. The temperature can be extracted from the time-of-flight images51.

It should be mentioned that, we can detect the numbers of double occupied sites to confirm whether the metal-Mott insulator transition happens. Firstly, we have to increase the depth of the optical lattice to prevent further tunneling of atoms. Next, the energy of the atoms on doubly occupied sites is shifted by approaching a Feshbach resonance. Then the one spin component of atoms on double occupied sites is transferred to a new magnetic sublevel by radio-frequency pulse method. Finally, the double occupancy can be deduced by the absorption images52,53.

To get Fermi surface in experimental, we ramp down the optical lattice slowly enough first and the atoms stay adiabatically in the lowest band while quasi-momentum is approximately conserved. Then the lattice potential is lowered to zero rapidly, by switching off the confining potential and the atoms can expand ballistically for several milliseconds. The Fermi surface can be obtained by a absorption image54,55.

Discussion

In this work, we have investigated the metal-insulator transition and magnetic phase transition in strongly correlated bilayer honeycomb lattice using cellular dynamical mean-field theory (CDMFT) combining with continue-time quantum Monte Carlo (CTQMC) method. In lower temperature case we map the phase diagram as a function of interaction U, inter-layer hopping t1 and magnetization m. It shows that the inter-layer hopping affects the electrons to form spin-polarized electrons and an insulating state is induced. A layer anti-ferromagnetic phase is found at large t1, in which the magnetization of dimer sites is zero while non-dimer keeps finite value. Therefore, the inter-layer hopping t1 plays an important role to form a singular magnetic spontaneous symmetry breaking phase. Our study may provide a helpful step for understanding the interaction and inter-layer hopping driven metal-insulator transition, the exotic magnetic order with asymmetry breaking and the possible magnetic-nonmagnetic order coexisting state.

Methods

The cellular dynamical mean-field theory

We combine the cellular dynamical mean-field theory (CDMFT) with continuous time quantum Monte Carlo (CTQMC) method to determine the metal-insulator transition and magnetic phase transition in the strongly correlated bilayer honeycomb lattice. In low-dimensional systems, quantum fluctuations are much stronger than the higher dimensions. The nonlocal effect is much important in this case. Dynamical mean-field theory ignoring the nonlocal correlations leads lots of errors in calculation. Therefore, we use CDMFT, as the advanced method in our work. We map the original lattice onto a 12-site effective cluster embedded in a self-consistent bath field [see Fig. 1(b)]. Starting with a guessing self-energy Σ(iω) (which is independent of momentum56), we can get the Weiss field G0(iω) obtained by the coarse-grained Dyson equation:

where iω is Fermionic Matsubara frequency, µ is the chemical potential, k is in the reduced Brillouin zone of the super-lattice and t(k) is hopping matrix for the super-lattice. The form of t(k) is:

where , , and a1, a2 are real lattice vectors as shown in Fig. 1(a). The cluster Green's function G(iω) can be gotten by the impurity solver. In our work, we use the numerically exact CTQMC simulation as impurity solver and take 5 × 106 QMC sweeps for each CDMFT loop42. The new self-energy Σ(iω) is recalculated by the Dyson equation:

This iterative loop repeated until self-energy is converged.

The CTQMC method as impurity solver can be taken as follows. We start the procedure at partition function, which can be written as:

where Tτ is time-ordering operator, is H1 in the interaction picture and is a partition function for the unperturbed term. Putting H1 = U Σini↓ni↑ in Eq. 4, the partition function is

Here 〈〉0 indicates a theromdynamic average with respect to . Using Wick's theorem, for each order in k, can be written as determinant detD(k):

where G0 is non-interacting Green's function. There is no spin index in D(k) for the determinants of spin-un and -down being equivalent. Like classical Monte Carlo, by integrand of Eq. 5, we can get the weight of order k

where δτ = β/L is slice of imaginary time. We can get the standard Metropolis acceptance ratio R of adding vertex by the detailed balance condition:

Here Pk→k+1 is the probability to increase the order from k to k + 1 (Pk+1→k the probability to decrease the order from k + 1 to k), is probability to choose a position in time and space for vertex you intend to add while is the probability to choose one vertex you intend to remove of from the existing k + 1 noes. To calculate the ratio R, we have to deal with the function detD(k + 1)/detD(k).

, we can easily get the value of λ in matrix form:

Then it is easy to obtain the update M for the order k + 1 by numerical method:

where the factor of the matrix is , Ri,j = G0(i, l)M(k)l,j and Li,j = M(k)i,lG0(l, j). For the step k − 1, we can also get the radio R and update formulas of M(k − 1):

Using the update formula for M, the Green's function can be obtained both in imaginary time and at Matsubara frequencies:

Here G0(iω) is a bare Green's function.