Abstract
If two elastic bodies with rough surfaces are first pressed against each other and then loaded tangentially, sliding will occur at the boundary of the contact area while the inner parts may still stick. With increasing tangential force, the sliding parts will expand while the sticking parts shrink and finally vanish. In this paper, we study the fractions of the contact area, tangential force and tangential stiffness, associated with the sticking portion of the contact area, as a function of the total applied tangential force up to the onset of full sliding. For the numerical analysis randomly rough, fractal surfaces are used, with the Hurst exponent H ranging from 0.1 to 0.9. Numerical simulations by boundary element method are compared with an analytical analysis in the framework of the Greenwood and Williamson (GW) model. In both cases, a universal linear dependency between the real contact area fraction in stick condition and the applied tangential force is found, regardless of the Hurst exponent of the rough surfaces. Regarding the dependence of the differential tangential stiffness on the tangential force, a linear relation is found in the GW case. For randomly rough surfaces, a nonlinear relation depending on H is derived.
Similar content being viewed by others
Introduction
Surface roughness plays a widespread role in many physical phenomena including friction, wear, sealing, adhesion, electrical and thermal conductivity as well as in the acoustic properties of contact interfaces. The main basic contributions to the understanding of the role of surface roughness in tribological contacts are due to Bowden and Tabor1, Archard2 and Greenwood and Williamson (GW)3. In the last decade, the contact of rough surfaces became once again a hot topic and the focus moved to the analysis of fractal, self-affine surfaces showing roughness in a wide range of wave vectors. In particular, the real contact area A between rough surfaces was shown to be almost exactly proportional to the normal load Fz4,5 in a wider range of normal forces than predicted by the GW theory

where ∇z is the rms slope of the surface and κ is a dimensionless factor. The reduced modulus of elasticity for two bodies in contact made of the same material is E* = E/(1 − v2) = 2G/(1 − v), with G being the modulus of shear and v the Poisson ratio. The normal contact stiffness kz of rough surfaces has been shown to be proportional to the normal load in the case of “nominally flat” surfaces (surfaces whose roughness power spectrum has a long wavelength cut-off or roll-off)6. For surfaces without a long wavelength cut-off, the contact stiffness kz was found to be a power function of normal load7,8:  , where z is the coordinate axis perpendicular to the surface and H is the Hurst exponent. Tangential contact of rough surfaces was studied in9,10 and11. In particular, in9 it was shown that the ratio of normal and tangential stiffnesses in a complete stick-contact remains the same as in the case of single rotationally symmetric contacts (Cattaneo and Mindlin ratio12,13). In11, this result was confirmed with surfaces of GW type and the tangential stiffness was found to rise linearly with the normal load in that case.
, where z is the coordinate axis perpendicular to the surface and H is the Hurst exponent. Tangential contact of rough surfaces was studied in9,10 and11. In particular, in9 it was shown that the ratio of normal and tangential stiffnesses in a complete stick-contact remains the same as in the case of single rotationally symmetric contacts (Cattaneo and Mindlin ratio12,13). In11, this result was confirmed with surfaces of GW type and the tangential stiffness was found to rise linearly with the normal load in that case.
In10, it was shown that in the case of partial slip, also the maximum tangential “pre-slip” distance is related to the indentation depth in the same way as in a single rotationally symmetric contact.
So far, important properties of rough contacts that are connected with the stick and slip regions of a tangential contact have not been investigated in detail. Yet the separate investigation of the stick and slip parts of the real contact area is relevant for many physical applications. For example, the differential tangential stiffness is only dependent on the current configuration of the stick region of contact. If bodies are subjected to tangential oscillation with a small amplitude (smaller than the maximum slip amplitude up to complete sliding), then wear will occur only in the slip-region (fretting). As shown by Ciavarella and Hills14 for arbitrary two-dimensional contacts and in15 for three-dimensional axis-symmetrical contacts, during fretting, the initial stick region always stays in the stick state (both at a constant normal force and a constant indentation), while in the initial sliding region the surfaces finally loose contact completely. This leads to changes in stiffness as well as electrical and thermal conductivity, which in the final state will only depend on the initial configuration of the stick region. The area of the stick region is also of interest, for example for impurity-film resistance of contacts. The decomposition of the contact area into stick und slip parts plays an important role in further practical problems such as frictional energy dissipation16,17, geotechnical engineering18, damping and stiffness of joints19 and control engineering20.
In the present paper, we investigate the dependence of the sticking part of the contact area on the normal and tangential force, as well as its contribution to the total tangential force and to the total tangential stiffness. The investigation is based on the classical solutions for tangential contacts going back to the works by Cattaneo11 and Mindlin13, which later have been generalized to arbitrary rough contacts by Ciavarella21,22 and independently by Jäger23. They have proven that the solution of the tangential contact problem can be gained from the linear superposition of two normal solutions, one corresponding to the limiting frictional traction distribution and a negative correction due to a distribution equal to the coefficient of friction multiplied by the normal contact pressure distribution corresponding to some lower value of the normal load. Numerical implementation of this technique was discussed in24 and its extension to a more general loading case consisting in an oscillatory tangential force is available in25. To date, although the mathematical theory and the numerical methods for the solution of this problem are established, the properties of the tangential contact solution for rough surfaces have been only marginally analysed. For smooth surfaces like spheres or cylinders, it has been shown in26 that the tangential force component acting in the stick region Fx,stick and the real stick area Astick are both nonlinear functions of the total tangential force Fx. We will show theoretically and numerically how these trends are modified in the case of rough surfaces. In particular, we will show that for the stick area a very universal linear dependence is valid, which practically does not depend on the character of roughness. When considering a tangential load that is monotonically rising, then the load has a biunique relation to the tangential displacement. In the numerical and analytical treatment of the problem, we will always impose the displacement and deduce the relevant quantities and then express everything with respect to the tangential force at that point, in order to give an intuitive physical interpretation of the contact problem.
Results
Partial slip in multi-asperity modelling
For simplicity, consider a contact of an elastic half space having a flat surface with a rigid rough counterpart and assume that in each point of real contact the Coulomb's law of friction with a constant coefficient of friction μ is valid. We start our consideration with the basic version of the Greenwood and Williamson (GW) model3 and show later that its result is robust and does not depend on most of the assumptions on which the GW model is based.
A nominally flat rough surface, consisting of a large number of independent “asperities”, each having the same radius of curvature R, is brought into contact with an elastic half space. The final result does depend only very weakly on the exact form of the probability density function Φ(z) of the height distribution. For simplicity, the probability distribution function is assumed to have an exponential form:

where λ is a characteristic length parameter of the height distribution (“roughness”).
First consider one single parabolic asperity subjected to a normal force Fz,0 kept constant during the application of the tangential load, see fig. 1. Quantities named with ‘0’ in the subscript refer to the case of a single asperity.
The contact radius a0, the indentation depth d0, the radius of the stick region c0 and the tangential displacement ux are connected by the relation27

where, G* = 4G/(2 − v) is the reduced shear modulus and  applies. The maximum tangential displacement
applies. The maximum tangential displacement  up to the start of the full sliding can be found by setting c0 = 0 in (3) and is equal to
up to the start of the full sliding can be found by setting c0 = 0 in (3) and is equal to

At given  , full sliding takes place for all asperities for which 0 < d0 < dmin,0 with
, full sliding takes place for all asperities for which 0 < d0 < dmin,0 with

In contrast, if the indentation depth d0 of an asperity is larger than dmin,0, the asperity will be in the state of a partial slip. The normal force is given by the Hertzian equation28

The tangential force and the stick area for partial sliding are given by29

and

For full sliding we find

and

Now we assume that the elastic half space is indented to the height z = h. The total stick area for a given tangential displacement ux is given by the integration of Eq. (8) over all the asperities that are high enough to have the indentation depth dmin necessary for achieving the partial sliding regime

where A0 is the true contact area obtained from the normal contact. This corresponds also to the initial stick area for a vanishing tangential displacement ux.
The total tangential force is calculated by integration of (7) over all asperities in the state of partial sliding and of (9) over all asperities in complete sliding:

By substitution z − h → z and introduction of the notation

we can rewrite (12) in the form

From Eq. (11) and Eq. (14) we finally get

Thus, for the classical GW model3 with an exponential distribution of asperity heights, we find linearity between the tangential force and the stick contact area. It can be shown easily that this result does not depend on the assumed parabolic shape of the asperities. Assumption of any other asperity form or the consideration of an ensemble of fractal rough asperities leads to the exact same result. Note that this result does not depend on the length parameter λ either. This fact implies a weak sensitivity of the solution with respect to the form of the probability distribution function. The only property needed for the derivation of Eq. (15) is a rapid (exponential) decay of the probability function.
Furthermore, Eq. (15) can also be obtained for many more cases using the analogy of the tangential and normal contact problem. Indeed, it follows from22 that in a tangential problem with partial slip, one can express the tangential stress τx in the stick region as the sum of a full-sliding term and a correction term 

where p is the pressure distribution. It shall be noted that  is a solution for pressure to the normal contact problem. This corrective solution has the initial sticking area as its contact area and
is a solution for pressure to the normal contact problem. This corrective solution has the initial sticking area as its contact area and

is the corresponding normal force. Integrating (16) over the whole contact area we find

When we are interested in quantities closely related to the stick region, it is sufficient to use the alternate normal contact solution at normal force Fz = Q*. This theorem holds whether the stick region is a compact area or split into multiple fractions. It can be shown that the indentation depth in this corrective normal contact problem reads

The major quantities related to the region of stick are the area and the tangential stiffness of this region. Solving for the area of stick and assuming the validity of Archard's law (1) we can write

thus finding a very general formulation of eq. (15) for all systems, where Archard's law holds. These can be like those statistically described by GW, but also other nominally flat surfaces or fractal rough surfaces.
For the normal contact stiffness as a function of the applied load, let us assume a general power-law dependency with exponent α, which is also expected from dimensional analysis considerations based on incomplete self-similarity30:

For any (mostly isotropic) contact region, the tangential stiffness is

and we find for the tangential stiffness of the stick region

For fractal rough surfaces with Hurst exponent H and no cut-off or roll-off in the PSD7,8:

so we find in dimensionless variables

In the case of nominally flat surfaces, the PSD must be limited in the long-wavelength-part, e.g. by either a cut-off, or a roll-off (constant PSD). The latter case formally corresponds to H = −1, so α ≈ 1 (see reference 8). The GW model also describes a particular type of nominally flat surface and for both cases we expect a linear dependency

It shall be noted that even though we can state general properties about the corrective stresses inside the stick zone, no general conclusion can be drawn regarding the stick force, because the pressure distribution inside the stick region is unknown.
Nevertheless, we can do this kind of analysis for the GW model in case of an exponential distribution of asperity heights, where all quantities can be determined in closed form. Indeed, the integrals from Eq. (12) can also be separated in order to distinguish between the tangential stick force and the slip force. The slip force includes a component from asperities in partial slip and another from full-slipping asperities. After some lengthy manipulation that we omit here for the sake of brevity, we find


where b = dmin/λ.
Numerical (BEM) results for fractal surfaces
Using the boundary element method (BEM) applied to numerically generated fractal rough surfaces, we find the stick area to follow (15) very closely, see Fig. 2. This result holds for all values of H that we investigated in the range from 0.1 to 0.9. For each value of H, 20 surfaces are generated and the bars of dispersion are plotted over the average response, to provide information about the scatter in the numerical results. It is very interesting to see linearity especially for H ≈ 1 with a very small deviation from it. This result underlines once again that the distribution of surface height is irrelevant to the problem, because in the case of fractal surfaces it is far from being exponential (see reference 31 for a statistical analysis of the height field of surfaces generated using the random midpoint displacement method). Second, the elastic interactions neglected in the original GW theory used here and accounted for using BEM certainly play an important role on the traction distributions for fractal surfaces with large H, as also demonstrated for the normal load scenario in32. Thus, numerical results validate the relation (15).
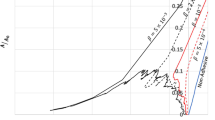
The dependence of the normalized differential tangential stiffness on the normalized force is shown in Fig. 3. While for small Hurst exponents in the vicinity of H = 0, the dependence is close to the linear relation (26), for higher Hurst exponents, the GW Equation is not supported by numerical results, but approaches eq. (25).
Numerical dependency of the normalized differential tangential stiffness as a function of the normalized tangential load.
Bars denote a confidence interval of 95% with respect to the average result. Numerical data support the dependency (25) shown in dotted lines. For H = 0.1, the greatest discrepancy is found. This is likely to be related to the fact that for small H, eq. (24) depends on the grid resolution, see [8].
The fraction of the stick component in the generated tangential force is shown in Fig. 4. For small tangential forces, almost the whole contact domain is in the stick-state, so the stick force is almost identical to the overall tangential force. With increasing tangential load, more and more contact spots slip, causing the relative stick force to decrease. When the tangential force reaches its maximum value given by the normal force times the coefficient of friction, the stick areas vanish and so does the stick tangential force. Surprisingly, the numerical results for the surfaces with H = 0.9, which by definition have strong asperity interactions, provide the closest trend to the GW prediction (27) plotted with solid line in the same figure.
Dependency of the normalized tangential load carried only by sticking regions as a function of the normalized overall tangential load.
Numerical results are given for three values of the Hurst exponent H, with confidence interval of 95%. The solid green line shows the analytical dependency resulting from GW model, Eq. (27) together with Eq. (14).
An example of evolution of the stick and slip contact domains is shown in Fig. 5.
Evolution of the stick/slip contact domains obtained using BEM for an increasing tangential force.
Black areas denote stick regions, grey is for sliding regions, white means no contact. With increasing tangential force (left to right), slip regions grow from regions supporting lower normal forces up to the whole contact area.
Discussion
To conclude, we found a linear relation between the stick area Astick and tangential force Fx for nominally flat rough surfaces in the framework of the GW contact theory and for general tangential contacts where Archard's law holds. The results are quite universal and are completely supported by direct numerical simulations of contacts with self-affine rough surfaces with Hurst exponents in the interval from 0.1 to 0.9. We further investigated the differential tangential stiffness both theoretically and by means of direct BEM simulations. The theory predicts a linear dependency for nominally flat surfaces and H ≈ 0. Indeed, numerical results show this linear dependency in the limit of small Hurst exponents and transition to a power-law behaviour  that is closely related to the normal contact response. This result is obtained assuming the validity of the Ciavarella/Jäger-principle and applying eq. (21),(24).
that is closely related to the normal contact response. This result is obtained assuming the validity of the Ciavarella/Jäger-principle and applying eq. (21),(24).
Finally, we investigated the stick component of the tangential force and we found characteristic bell-shape curves for both the numerical samples and for the GW theory. The maximum value of these curves for fractal surfaces depends on the Hurst exponent H.
Methods
BEM calculations
The 3D Boundary element method was used to solve the problem of tangential contact with partial slip. As a first step, the normal contact must be solved using an iterative scheme. As a result, the apparent area of contact is partitioned into two sections. Discrete grid points that are considered to be in contact are all deflected to the same height and have positive pressure. All other points are not in contact, so they have zero pressure and a positive gap width. We used the CG-approach proposed by Polonsky and Keer33.
In the next step, a tangential displacement ux is applied. This time, the true contact area from the first step is again divided into two parts. On the one hand there can be points that are in stick state, which means their local tangential displacement is equal to ux and their tangential stress must be smaller that the local normal pressure times the coefficient of friction. On the other hand, points can be in sliding state, so their tangential stress is equal to the coefficient of friction times the normal pressure. A correct partitioning is found iteratively. In order to do so, we start from an arbitrary partitioning and we apply the tangential stress τ = μp in the slip zone. After that, the tangential stresses in the stick zone are solved demanding that the tangential displacement here shall be constant ux. In case any grid point from the slip zone was deflected more than ux or any point from the stick zone results with stresses greater than μp, then these points are transferred to the other state.
All discrete grid points influence each other via the elastic coupling, according to a discrete formulation of the Cerruti formula for a single force acting upon the elastic half-space. We used the Cattaneo-Mindlin analogy, assuming that the elastic coupling parallel to the surface can be expressed in the same way as normal deflections (Boussinesq), only modified by a coefficient of proportionality. We also performed BEM calculations considering the full anisotropic Cerruti solution and we get indistinguishable results. A comprehensive formulation of a partial-slip-algorithm can be found in34.
We generated self-affine surfaces with Hurst exponents from 0.1 to 0.9 using the random midpoint algorithm. For these surfaces we solved the partial-slip problem for a range of tangential displacements ux and recorded the resulting tangential force and size of the stick area. The simulations have been carried out for square contacts with free boundary conditions outside the contact region.
References
Bowden, F. P. & Tabor, D. The Friction And Lubrication Of Solids (Clarendon Press, Oxford, 1986).
Archard, J. F. Elastic deformation and the laws of friction. Proc. R. Soc. A 243, 190 (1957).
Greenwood, J. A. & Williamson, J. B. P. Contact of nominally flat surfaces. Proc. R. Soc. A 295, 300 (1966).
Hyun, S. & Robbins, M. O. Elastic contact between rough surfaces: effect of roughness at large and small wavelengths. Tribol. Intern. 40, 1413 (2007).
Campana, C. & Müser, M. H. Practical Green's function approach to the simulation of elastic semi-infinite solids. Phys. Rev. B 74, 075420 (2006).
Akarapu, S., Sharp, T. & Robbins, M. O. Stiffness of contacts between rough surfaces. Phys. Rev. Lett. 106, 204301 (2011).
Pohrt, R. & Popov, V. L. Normal contact stiffness of elastic solids with fractal rough surfaces. Phys. Rev. Lett. 108, 104301 (2012).
Pohrt, R. & Popov, V. L. Contact stiffness of randomly rough surfaces. Sci. Rep. 3, 3293 (2013).
Campana, C., Persson, B. N. J. & Müser, M. H. J. Phys., Transverse and normal interfacial stiffness of solids with randomly rough surfaces. J. Phys.: Condensed Matter 23, 085001 (2011).
Grzemba, B., Pohrt, R., Teidelt, E. & Popov, V. L. Maximum Micro-Slip in Tangential Contact of Randomly Rough Self-Affine Surfaces. Wear 309, N. 1–2, p. 256–258 (2014).
Medina, S., Nowell, D. & Dini, D. Analytical and Numerical Models for Tangential Stiffness of Rough Elastic Contacts. Tribol. Lett. 49, 103–114 (2013).
Cattaneo, C. Sul contatto di due corpi elastici: distribuzione locale degli sforzi. Rendiconti dell'Accademia Nazionale dei Lincei, Series 6, 27, 342–348, 434–436, 474–478 (1938).
Mindlin, R. D. Compliance of elastic bodies in contact. ASME J. App. Mech. 16, 259–268 (1949).
Ciavarella, M. & Hills, D. A. Brief Note: Some observations on the Oscillating Tangential Forces and Wear in General Plane Contacts. Eur. J. Mech. - A/Solids 18, 491–497 (1999).
Popov, V. L. Analytic solution for the limiting shape of profiles due to fretting wear. Sci. Rep. 4, 3749 (2014).
Dini, D. & Hills, D. A. Frictional energy dissipation in a rough Hertzian contact. ASME J. Trib. 131, 021401 (2009).
Barber, J. R., Davies, M. & Hills, D. A. Frictional elastic contact with periodic loading. Int. J. Solids Struct. 48, 2041–2047 (2011).
Desai, C. S., Drumm, E. C. & Zaman, M. M. Cyclic interface and joint shear device including pore pressure effects. ASCE J. Geotechnical Eng. 111, 793–815 (1985).
Kirsanova, V. N. The shear compliance of flat joints. Machine and Tooling 38, 30–34 (1967).
Harnoy, A., Friedland, B. & Rachoor, H. Modeling and simulation of elastic and friction forces in lubricated bearings for precise motion control. Wear 172, 155–165 (1994).
Ciavarella, M. The generalized Cattaneo partial slip plane contact problem. I-Theory, II-Examples. Int. J. Solids Struct. 35, 2349–2378 (1998).
Ciavarella, M. Tangential loading of general three-dimensional contacts. ASME J. Appl. Mech. 64, 998–1003 (1998).
Jäger, J. A new principle in contact mechanics. ASME J. Trib. 120, 677–684 (1998).
Borri Brunetto, M., Chiaia, B. & Ciavarella, M. Incipient sliding of rough surfaces in contact: a multiscale numerical analysis. Comput. Methods in Appl. Mech. Eng. 190, 6053–6073 (2001).
Borri Brunetto, M., Carpinteri, A., Invernizzi, S. & Paggi, M. Micro-slip of rough surfaces under cyclic tangential loading. In: Analysis and Simulation of Contact Problems. LN. App. M. Springer, 27, 333–340 (2006).
Carpinteri, A., Paggi, M. & Zavarise, G. Cusp-catastrophe interpretation of the stick-slip behaviour of rough surfaces. Comput. Model. Eng. Sci. 53, 1–23, 1526-1492 (2009).
Johnson, K. L. Ch.7 Contact Mechanics (Cambridge University Press, Cambridge, 1985).
Hertz, H. Über die Berührung fester elastischer Körper. J. für die Reine und Angewandte Mathematik 92, 156–15 (1881).
Popov, V. L. Contact Mechanics And Friction. Physical Principles And Applications (Springer-Verlag, Berlin, 2010).
Paggi, M. & Barber, J. R. Contact conductance of rough surfaces composed of modified RMD patches. Intern. J. Heat Mass Transf. 54, 4664–4672 (2011).
Zavarise, G., Borri-Brunetto, M. & Paggi, M. On the reliability of microscopical contact models. Wear 257, 229–245 (2004).
Ciavarella, M., Greenwood, J. A. & Paggi, M. Inclusion of “interaction” in the Greenwood and Williamson contact theory. Wear 265, 729–734.
Polonsky, I. A. & Keer, L. M. A numerical method for solving rough contact problems based on the multi-level multi-summation and conjugate gradient techniques. Wear 231, 206–210 (1999).
Pohrt, R. & Li, Q. Complete Boundary Element Formulation for Normal and Tangential Contact Problems. Phys. Mesomech. accepted, 1–12. (2014).
Acknowledgements
The research leading to these results has received funding from the European Research Council under the European Union's Seventh Framework Programme (FP/2007–2013)/ERC Grant Agreement n. 306622 (ERC Starting Grant “Multi-field and multi-scale Computational Approach to Design and Durability of PhotoVoltaic Modules” - CA2PVM, Principal Investigator: M. Paggi). The support of the Italian Ministry of Education, University and Research to the project FIRB 2010 Future in Research “Structural mechanics models for renewable energy applications” (RBFR107AKG, Principal Investigator: M. Paggi) is also gratefully acknowledged. The German authors acknowledge the financial support by the Deutsche Forschungsgemeinschaft (DFG) and by COST Action MP1303.
Author information
Authors and Affiliations
Contributions
M.P. and R.P. performed the BEM calculations. R.P. prepared the figures. V.L.P., M.P. and R.P. carried out the analytical analysis and contributed to the writing of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. The images in this article are included in the article's Creative Commons license, unless indicated otherwise in the image credit; if the image is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the image. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Paggi, M., Pohrt, R. & Popov, V. Partial-slip frictional response of rough surfaces. Sci Rep 4, 5178 (2014). https://doi.org/10.1038/srep05178
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep05178
This article is cited by
-
Plastic deformation effect on contact behaviour in granular materials
Granular Matter (2024)
-
Approximate contact solutions for non-axisymmetric homogeneous and power-law graded elastic bodies: A practical tool for design engineers and tribologists
Friction (2024)
-
A Fully Coupled Normal and Tangential Contact Model to Investigate the Effect of Surface Roughness on the Partial Slip of Dissimilar Elastic Materials
Tribology Letters (2022)
-
Indentation of a surface-stiffened elastic substrate
Scientific Reports (2018)
-
Numerical Modeling Describing the Effects of Heterogeneous Distributions of Asperities on the Quasi-static Evolution of Frictional Slip
Rock Mechanics and Rock Engineering (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.