Introduction

Recent discoveries of skyrmionic configurations in magnetic and multiferroic systems1,2,3, the writing and deletion of single magnetic skyrmions4 and ultrafast current-driven gyrotropic switching5,6 and oscillations7 of magnetic vortices have fueled interest in the properties of topologically nontrivial magnetization textures such as vortices and skyrmionic configurations. For the vortex spin texture, analytical studies and numerical micromagnetic simulations8,9 had predicted the formation of stable vortex configuration with core radius of the order of the magnetic exchange length for ultra-thin disks with sufficiently large lateral dimensions. Actual experimental observation of magnetic vortices was first achieved by Shinjo et al.10 in permalloy. Subsequent theoretical and experimental research investigated the possibility of vortex-based memories5,11,12,13. For the skyrmion spin texture, Bogdanov et al. theoretically predict the formation of skyrmions in magnetic systems which is stabilized by the Dzyaloshinskii-Moriya (DM) interaction14,15,16. Numerical micromagnetic studies17,18,19 showed that the size of the skyrmions scales as (D/Jex), where D is the DM interaction strength and Jex is the exchange coupling strength. For typical magnetic parameters, the skyrmionic structure is stable for DM strength of between 5 < D < 15 (mJ/m2)19. Experimental confirmation of the existence of skyrmionic configurations was recently attained via neutron scattering and Lorentz transmission electron microscopy1,2. Subsequent research on the electron transport and current-driven dynamics of skyrmionic systems has indicated their potential use in spintronic applications specifically in memory18,20,21. More recent experimental demonstrations of the generation and visualization of molecular bound skyrmions22 and thermally driven ratchet motion of a skyrmion microcrystals23 allude to the rich underlying physics of magnetic skyrmions.

Both the vortex and skyrmion configurations are associated with topological properties, such as the Berry or geometric phase, which are quantized and invariant to any smooth deformations24. For instance, it has been shown that relativistic electron vortex beams have an associated geometric phase that governs their dynamics25. The first example of such topological transport in condensed matter physics is discovered in the context of the quantum Hall effect, as described by Thouless et al. and Kohmoto26,27. Subsequently, the anomalous Hall effect in a medium with spin-orbit coupling was also shown to have a topological basis28. More recently, the gauge formalism was used to describe topological transport in various spin-orbital and magnetic systems29,30,31. The insensitivity of these topological invariants to deformations and fluctuations which invariably attend to any physical system, makes them attractive candidates for device applications. As devices shrink in size, the influence of external noise and disturbances becomes ever more significant, thus increasing the appeal of stable topologically-linked device output. By linking these invariants to some measurable property of the magnetic system or device, one may obtain an output which is naturally quantized (digital) and robust to noise and fluctuations. The topological Hall conductivity (THC), first described in chiral pyrochlore material, is one such property28. Under adiabatic conditions, the THC has been shown to be related to the quantized magnetic flux of the topological magnetic (B) field. However, the quantized flux value strictly holds only for ideal skyrmion or vortex configurations, which are spatially infinite in extent and are unaffected by any edge effects.

Thus, in this paper, we analyze the THC under the non-ideal situation of (i) finite size and (ii) in the presence of edge interactions. These two factors will become increasingly important in ultra-small magnetic skyrmion and vortex elements, which may be potentially used in memory application. In particular, there are proposals to utilize the topological properties of vortex elements (such as its polarity and chirality) to store binary bits of information6,32. In such an application, the THC may provide a high-fidelity read-back scheme, which is less susceptible to, e.g., incomplete switching or geometrical non-uniformities of the elements. Under adiabatic condition, we analyze the THC for both skyrmion and vortex patterns. In the presence of edge effects, we mapped the configuration onto the unit Bloch sphere, which provides us with an intuitive picture of the influence of edge effect on the THE. From this mapping, we derived the analytical expression for the THC, which was verified by direct numerical integration. The THE was found to be dependent only on the magnetization at the edges (which demarcates the boundary on the Bloch sphere). This suggests that “edge engineering” of elements may be utilized to achieve the desired THE output. By analyzing the Berry phase associated with the vortex and skyrmion configurations, it was shown that edge interactions in vortex elements can improve the THC output by bringing it closer to the ideal quantized value, but tend to have the opposite effect for skyrmion elements. However, for vortices with higher winding numbers, the improvement of the THC output is reduced.

Results

Hamiltonian and Topological Hall Conductivity

Conduction electrons moving in a two-dimensional medium with a spatially varying spin texture can be modelled by the Hamiltonian:

where

is the direction of the local magnetization, which varies smoothly with position r in the medium and (θ, ϕ) are the angles in spin space. Applying a gauge transformation to align the reference spin axis to the local magnetization direction (see Methods), the Hamiltonian is then transformed to

where the gauge potential is A = −iΦ0U†∇U, with being the flux quantum. In the adiabatic limit, where the electron spin relaxes to the local magnetization orientation, the off-diagonal components of the gauge potential go to zero. The gauge potential then corresponds to that of a magnetic monopole, i.e., in Bloch (spin) space. By transforming the gauge to the spatial (e.g., Cartesian) coordinates and taking the curvature we can derive the effective B-field associated with the local magnetization distribution (spin texture) – see Methods. We also discuss the applicability of the adiabatic limit in the systems under consideration (see Methods).

If the spin texture varies over the x-y plane and has no z-dependence, then only the vertical (z) component of the topological field will be non-zero. This may be expressed in terms of the spin texture as (see Methods):

This topological field induces a transverse Lorentz force on the electron. It is this transverse force acting on the conduction electrons which gives rise to the topological Hall conductivity (THC). From the semiclassical Drude theory, the THC is related to the topological magnetic flux29, i.e.,

where (see Methods for the derivation of the above). Here, τ is the scattering time, m is the electron mass, is the longitudinal conductivity, S is the sample area and is the averaged vertical field over S.

The more experimentally relevant parameter is the Hall resistivity, which is given by 33, where the approximation holds in the low field limit. Thus, in this limit both the Hall resistivity and conductivity are proportional to the topological flux. The above proportionality of σxy and ρsy to the topological flux is obtained by considering the semiclassical Drude model. This proportionality still holds in the quantum regime, as can be shown by applying the approach of Tatara et al.34 (see Methods).

Topological Hall Conductivity of Vortex and Skyrmion Textures

Next, we consider the specific case of spin textures exhibiting axial symmetry, such as the vortex and skyrmion configurations, for which the topological flux expression assumes an especially simple form. For these configurations, the polar and the azimuthal angles of the spin orientation (θ, ϕ) can be expressed as

In the above, a is the core radius of the vortex or skyrmion and denotes the characteristic size of the vortex/skyrmion texture, (r, φ) are the cylindrical coordinates in real space, while W, P = ±1 and C = ±1 denote the winding number, polarity and chirality, respectively. The topological invariants such as polarity P and winding number W are linked to electronic transport properties in skyrmion/vortex textures in the adiabatic limit. Since these quantities are quantized and invariant to small deformations, they render the electronic transport to be robust to noise and other fluctuations as mentioned earlier. The gradient operator, in cylindrical coordinates, is given by and thus it follows from Eq. (21) that the topological B-field for the vortex and skyrmionic configurations in polar coordinates are, respectively, given by

Note that the topological field is independent of the chirality C. This is because, as can be seen in the above equations, the change in chirality involves just a constant phase difference of Δϕ = π in the azimuth of the spin orientation. From the topological field in Eq. (7), the corresponding flux emanating over a circular vortex/skyrmion element of radius R, is given by

where nv,s = 1 (2), for the vortex (skyrmion) configurations. In the limit of infinite vortex/skyrmion element, the flux corresponds to a topological invariant with quantized values, i.e.,

Since the above flux can be related to the Hall conductivity, as can be seen from Eq. (5), thus the Hall conductivity arising from ideal vortex and skyrmion textures of infinite extent will be quantized and topological in nature.

For further analysis (e.g., into the edge effects), it is instructive to see how the flux in real space (or any arbitrary space for that matter) translates into the flux in spin space. Discounting the factor of , the topological flux in real space is given by

where S′ is the enclosed region in spin space. In Eq. (10), we have made use of Eq. (23) in the second line and the fact that is the Jacobian for the transformation between the Cartesian (x, y) to the spin (θ, ϕ) spaces. Since and that represents the differential area element on the unit sphere (equivalent to the solid angle dΩ, as shown in Fig. 1), Eq. (10) immediately leads to

Thus, the THC can be mapped to the solid angle ΩS′ subtended by the spin texture in spin space. ΩS′ corresponds to the Berry or geometric phase of the adiabatic electronic transport through the spin texture. It thus follows, that for axially symmetric spin configurations of winding number W (i.e., θ = θ(r) and ϕ = Wφ + ϕ0, where ϕ0 is some constant offset), that the spin texture will be mapped onto a spherical cap in spin space. The THC would then assume a simple analytical form:

where R is the radius of the spin texture element in real space. By considering Eq. (6), we recover the flux expression of Eq. (8). Finally, for vortex (skyrmion) textures of infinite extent (i.e., as R → ∞), cosθ(R) → 0 (−P) and thus we obtain the quantized flux quantity of Eq. (9).

Figure 1
figure 1

The above depicts the area element dA on the unit Bloch sphere in spin space, which is given by , whose magnitude represents the solid angle subtended by dA.

Full size image

Edge Effects on the Topological Hall Conductivity

Besides recovering the flux expression obtained earlier by algebraic means, the above transformation of the spatial spin texture to the Bloch sphere in spin space also provides a pictorial representation of the THC. We find that the flux of axially symmetric spin textures contributing to the THC can be mapped to the solid angle or spherical cap on the unit Bloch sphere. With this theoretical insight we can now analyze the THC of an “edged” vortex or skyrmion texture, where there exists an edge anisotropy which tends to align the magnetization along the element boundary, i.e., in the azimuthal direction . In general, the edge effect can be modelled by modifying the original magnetization direction to

where

The parameter s0 denotes the strength of the edge anisotropy, while λ is the length-scale over which it acts. Edge anisotropy causes the magnetization to be aligned along the edge of a magnetic element so as to lower the magnetic pole density at the boundary and minimize the free energy of the system35,36. The strength of the edge anisotropy s0 is proportional to the discontinuity in the saturation magnetization ΔMs across the boundary, while its characteristic decay length is given by , where A is the exchange constant and µ0 is the permeability of vacuum. Note that the second term in the first line of Eq. (14) arises from the edge interaction from the diametrically opposite segment of the boundary, assuming that the edge interaction decays exponentially as we move away from the boundary towards the vortex/skyrmion core. For the case of vortex/skyrmion texture of unit winding number (W = 1), the azimuthal spin orientation is already parallel to the direction of the edge interaction as can be seen from Eq. (6). Thus, in this special case, the edge interaction would only modify the polar angle, which is now given by

where s = |s| and cos θ is given by Eq. (6), with the winding number W = 1.

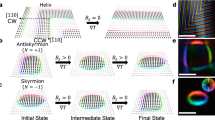
For the vortex configuration, the presence of the edge interaction causes the spin orientation to align away from the polar direction. This has the effect of “stretching” downwards the boundary of the spherical cap on the Bloch sphere closer to the equatorial plane, thus increasing the subtended solid angle or Berry phase Ω [see Fig. 2(a)]. Since Ω is directly related to ΦB [see Eq. (11)] and hence to the THC and that the ideal topological THC value corresponds to Ω = π for a vortex of unit winding number [see Eq. (9)], the presence of the edge interaction would tend to “improve” the THC towards the ideal value. In other words, a vortex element of finite radius R which originally yields a flux of , would now yield a flux of [P − cos θ′(R, s)]πΦ0 in the presence of edge anisotropy. This flux value is closer to the quantized value of PπΦ0 which emanates from an ideal vortex of infinite size. In other words, as far as the THC is concerned, a finite vortex element with edge anisotropy is effectively equivalent to an ideal vortex (without edge effect) of a larger radius.

Figure 2
figure 2

(a) and (b) show the Bloch spheres corresponding to a vortex and skyrmion elements, respectively. For both configurations, the dark blue spherical cap refers to the solid angle Ω of the Bloch sphere or the Berry phase contributing to the topological flux and hence the THC, in the absence of edge interactions. In the presence of edge interactions, the boundaries of the spherical caps are stretched downwards (upwards) for the vortex (skyrmion) configurations, towards the equatorial plane. This brings the solid angle or the Berry phase closer to the ideal value of Ω = π for the vortex texture, but away from the ideal value of Ω = 2π for the skyrmion texture. (c) and (d) The contour plots of the topological Hall conductivity (THC) for (a) the vortex and (b) skyrmion configurations of positive polarity (P = 1) and unit winding number (W = 1), calculated based on Eq. (16) as a function of element size R and edge anisotropy strength s0. The THC is expressed in units of for the vortex (skyrmion) configurations, which corresponds to the ideal THC value due to a vortex (skyrmion) of infinite extent. The above calculated THC values coincide exactly with the analytical THC result given by Eq. (12), assuming a polar angle of Eq. (15).

Full size image

For the skyrmion texture, however, the effect of the edge interaction is more complicated and depends on the angular extent of the original spherical cap Ω = [P − cos θ(R)]π, in the absence of edge interaction. If (R/a) < 1, then Ω < Pπ from Eq. (8), i.e., the original spherical cap is wholly within the top hemisphere. Then, the edge interaction would have the effect of stretching downwards the boundary of the spherical cap to the equatorial plane, thus bringing the solid angle or Berry phase closer to the ideal value of Ω = 2Pπ. However, when (R/a) > 1, the original spherical cap in the absence of edge interaction extends beyond the equator. The effect of edge interaction would be to “pull” upwards the boundary of the cap towards the equatorial plane [see Fig. 2(b]. The resulting solid angle/Berry phase is reduced and diverges away from the ideal value of Ω = 2Pπ. In the special case where the element size coincides with the skyrmion core radius, i.e., R = a, the spherical cap is already hemispherical in the absence of edge interaction. The magnetization direction along the boundary of the skyrmion element coincides with the edge anisotropy direction (both along the azimuthal direction). Hence, the addition of edge interaction will neither change the magnetization direction at the boundary nor the subtended solid angle Ω. Thus, the THC has a constant value of corresponding to Ω = Pπ regardless of the edge anisotropy strength s0, as shown by the vertical contour line corresponding to (R/a) = 1 in Fig. 2(d).

Numerical verification

The above theoretical analysis is verified by numerical calculation of the flux via direct integration of the z-component of the B field over a vortex/skyrmion element of size R, in the presence of an edge anisotropy strength s. For a general spin texture (r, φ), the corresponding B-field can be evaluated from Eq. (21) as

After substituting the spin texture of Eq. (13) into the above to obtain the topological field, the numerical value of the resulting flux over the vortex/skyrmion element is then obtained via the integration: . The calculated flux value is found to coincide (within numerical accuracy) to the analytical prediction of cosθ′(R, s)PπΦ0, where cosθ′(R, s) is given by Eq. (15).

Discussion

Our analysis in the previous section has shown that the THC is determined by the solid angle subtended by the spin texture in the Bloch space, which is equivalent to the Berry phase associated with the adiabatic transport through the texture. To explore this idea further, we consider the THC for a family of skyrmionic configurations, whose polar angle is defined as

where p is some even integer, while the azimuthal angle is given by Eq. (6). Note for the case of p = 2, we recover the skyrmion texture of Eq. (6), which was considered earlier. All the configurations defined by Eq. (17) exhibit the skyrmion pattern of θ(r) = 0 at r = 0 and θ(r) = π as r → ∞, i.e., with the spin texture pointing vertically up at the centre (origin) and vertically down at large distances from the origin and the transition between these two extremes occurring at around r = a. Now, the larger the value of p, the faster would be the transition or spin rotation at around r = a. Hence, for a skyrmion element of radius R > a, we would expect the skyrmion texture to subtend over a larger solid angle over the Bloch sphere corresponding to a larger Berry phase. Thus, the corresponding THC would increase and more closely approach the ideal THC value of of an infinite skyrmion. Numerical evaluation of the field via Eq. (16), followed by direct integration of the vertical flux over the skyrmion element confirms the predicted increase in the THC towards as p increases and the skyrmion transition gets sharper.

The analysis in the previous paragraph reveals an important insight on the THC of axially symmetric spin textures – since the THC is related to the spherical angle subtended in the Bloch space, it is thus determined solely by the spin configuration at the element boundary. In other words, the THC would not be affected by the spin distribution within the interior of the element. To illustrate this point, we compare the THC arising from two skyrmion elements whose edge interaction decays at different rates within the interior of the elements. If the decay lengths of the edge interaction are set at λ and 2λ for the two elements, their respective spin configurations are then given by

By setting the ratio of the edge interaction strengths at

the spin texture will be identical along the boundary of the two elements (i.e., at r = R), but would differ within the interior (r < R). However, their THC should be identical, since it is only dependent on the spin configuration at the boundaries. This is borne out by numerical flux calculation via Eq. (16) and direct integration. As shown in the inset of Fig. 3, by setting the edge anisotropy strengths according to Eq. (19), the two spin textures are made to coincide at the boundary of the skyrmion elements, but not within the interior. However, this difference does not affect the overall THC, as the THC values for the two spin textures are exactly identical (see main plot of Fig. 3). This has intriguing implications from the application standpoint – for skyrmionic and vortex elements, one can control the THC output merely by engineering the spin texture along the boundary without needing to consider the spatial variation of the magnetization within the element. Furthermore, the spin texture at the boundaries tends to be more amenable to external factors, e.g., by controlling the geometry of the boundaries, or by interfacing with other materials.

Figure 3
figure 3

Contour lines for THC in units of for skyrmion configurations of two different decay lengths L = λ and L = 2λ.

The contour lines for the latter exactly coincide with that of a skyrmion with decay length L = λ, but with a modified edge anisotropy strength of which is given by Eq. (19). The inset shows the spatial profile of the in-plane spin component as a function of distance r from the centre of a skyrmion element of size R = 2.5a, for the two decay lengths. The two spin configurations coincide at the boundary r = R.

Full size image

Now, we consider the THC arising from the vortex configuration of a higher winding number, i.e., for W = 2. In this case, the azimuthal angle of the spin orientation rotates faster than the tangential direction to the boundary element. Hence, there is an angular deviation of Δφ = (W − 1)φ between the direction of the edge interaction and the azimuthal orientation of the spin texture at the boundary. We would thus expect that the edge effect has a weaker effect in stabilizing the vortex texture, compared to the W = 1 case where the edge effect is always fully aligned to the azimuthal spin direction. In general, in the presence of edge interactions and for the higher winding numbers of W > 1, the spin orientation within the element is given by

where ϕ is given by Eq. (6), s is the interaction strength as given by Eq. (14). Note that the edge interaction acts along the tangent to the element boundary, which is denoted by the azimuthal angle of (ϕ − Δφ), while the strength of the edge interaction is modulated by the angular deviation Δφ between the magnetization and the edge. The spin texture denoted by Eq. (20) does not exhibit axial symmetry. However, one can still calculate the corresponding THC by transforming the spin texture to the Bloch sphere. For the case of W = 2, the spherical cap contributing to the THC would be “double-layered” since it winds around the Bloch sphere twice, while the polar angle of its boundary would vary at different azimuthal angle ϕ with its lower (upper) limits coinciding with the spherical caps of a unit winding number in the presence (absence) of the edge interaction at ϕ = 0 (π). Just as in the case of vortices with W = 1 (unit winding number) discussed earlier, the THC for W = 2 vortieces approaches the ideal value of Wσ0xy when the radius of the element far exceeds the core size, i.e., . However, by comparing Fig. 4(b) with Fig. 2(c), we find the THC for the W = 2 vortices are more weakly-dependent on the edge interaction compared to that of W = 1 vortices. This is because for the former case, the direction of the magnetization at the edges does not always coincide with that of the edge anisotropy (along the azimuthal direction). In the Bloch space, this weaker dependence can be seen schematically by the fact that the W = 2 spherical cap occupies a smaller solid angle than the W = 1 spherical cap in the presence of edge interactions [see Fig. 4(a)]. Thus, one can surmise that although utilizing vortex elements of winding number W = 2 may double the number of memory bits per element, the robustness of the bit elements would be less susceptible to edge engineering.

Figure 4
figure 4

(a) Bloch sphere showing a spherical cap (dark orange) corresponding to a vortex texture with a higher winding number, i.e., W = 2. The boundaries B1 and B2 correspond to the spherical cap for a W = 1 vortex (of unit winding number), in the presence and absence of edge interaction, respectively. (b) The contour plot of the corresponding THC in units of . The THC σxy approaches as R and s0 approaches infinity.

Full size image

Finally, we discuss the implementation of the read-out of memory based on the vortex or skyrmion configurations. The proposed device structure is shown in Fig. 5). For the vortex configuration, submicron sized nano-elements made of permalloy (NiFe) have been fabricated to a high degree of regularity and precision10,37. For the skyrmion configuration, regular circular elements of diameter ≈ 50 nm can be formed in a regular lattice in multiferroics such as Cu2OSeO33. Experimentally, the Hall output voltage is usually measured via a standard six terminal Hall probe configuration (see e.g.,38). For the proposed memory device, the Hall probe would have to be miniaturized. We propose a cross-point architecture to read out the THE output for a particular vortex/skyrmion cell element as shown in Fig. 5). Current would be passed through the column line passing through the element under consideration, while the THE voltage output is read across the corresponding row line. The proposed cross-point architecture has also been employed in other memory applications, e.g., in magnetic RAM chips, which employ cross-linked write and read current lines39.

Figure 5
figure 5

Proposed memory device based on magnetic elements with skyrmion/vortex configurations.

The memory read-out of a particular cell is effected via the THE output across the horizontal voltage line as current is passed through the vertical line, with the two lines intersecting at the cell being read.

Full size image

Methods

Gauge Potential and Effective Topological Field

To solve the Hamiltonian in Eq. (1) for any arbitrary , it is first diagonalized by a local gauge transformation, U(r), i.e., . The gauge U(r) is non-unique; a convenient choice is given by , where . The gauge transformation yields a gauge potential which corresponds to that of a magnetic monopole, i.e., in Bloch (spin) space. Since we are dealing with the topological gauge fields induced by a two-dimensional spatial spin texture, it is useful to transform them to the spatial (e.g., Cartesian) coordinates, as follows:

The curvature of the gauge potential yields the effective B-field, i.e.,

If the spin texture varies over the x-y plane and has no z-dependence, then only the vertical (z) component of the topological field will be non-zero, i.e.,

A more useful expression of the topological field can be obtained by considering the vector product . Since is a function of θ and ϕ, one can expand the product:

where the second equality follows directly from Eq. (2). From Eqs. (22) and (23), we have , from which the alternative expression for the topological field follows:

Semiclassical Derivation of the Topological Hall Conductivity

We present the derivation of the topological Hall conductivity (THC) leading to Eq. (5). By definition, the transverse conductivity is given by

In the presence of a vertical magnetic field (Bz), the transverse velocity vy is given by

where Fy = eBzvx is the transverse Lorentz force due to the vertical field Bz, τ is the scattering time and m is the electron mass. Substituting Eq. (26) into Eq. (25), we have

where we have made use of the definition . Averaging the vertical Bz-field over the spin texture element, i.e.,

and substituting the above into Eq. (27), we obtain Eq. (5) in the main text.

Applicability of the Adiabatic Approximation

In the adiabatic limit, the electron spin is assumed to have sufficient time to relax as it passes through and interacts with the local moments. Physically, the adiabatic limit is approached when the variation of the spin texture is gradual enough such that the probability of spin-flip transition can be neglected. In other words, , where ωq is the rate of change of and Δ is the energy-split between the spin-up and down electrons. Specifically, in our system, we have:

where vF is the Fermi energy and w is the characteristic length over which varies. The spin split in energy is given by Δ = 2J, where J is the s-d exchange energy. Thus, the adiabatic limit is satisfied under the following condition:

Assuming typical values for ferromagnetic metals of kF ≈ 1010 m−1, EF ≈ 5 eV, J ≈ 1 eV40 and vortex/skyrmion core radius of 20–40 nm, and thus the above adiabatic condition generally holds.

Derivation of Hall Resistivity in the Quantum Regime

The proportionality of the Hall conductivity and hence, the Hall resistivity to the topological flux [see Eq. (5)] was earlier shown via the semiclassical Drude model. This may also be shown in the quantum regime via the Kubo (linear response) formalism34. In this regime, the Hall resistivity is given by:

In the above, P is the spin polarization of current in the system and is the Fourier trnsform of the spatial gauge field. Note that the proportionality of ρxy (and hence σxy) to ΦB still holds in the quantum regime.