Abstract
The quest of novel compounds with special structures and unusual functionalities continues to be a central challenge to modern materials science. Even though their exact structures have puzzled scientists for decades, superhard transition-metal borides (TMBs) have long been believed to exist only in simple crystal structures. Here, we report on a polytypic phenomenon in superhard WB3 and MoB3 with a series of energetically degenerate structures due to the random stacking of metal layers amongst the interlocking boron layers. Such polytypism can create a multiphase solid-solution compound with a large number of interfaces amongst different polytypes and these interfaces will strongly hinder the interlayer sliding movement within each polytype, thereby further increase the hardness of this particular material. Furthermore, in contrast to the conventional knowledge that intrinsically strong chemical bonds in superhard materials should lead to high lattice thermal conductivity, the polytypic TMB3 manifest anomalously low lattice thermal conductivity due to structural disorders and phonon folding. These findings promise to open a new avenue to searching for novel superhard materials with additional functionalities.
Similar content being viewed by others
Introduction
Superhard materials are technologically important in many applications, from reducing the wear of everyday objects to creating machining tools. The hardness of a material is usually measured by indenter techniques and is thus determined by how resistant the bonds in the material are against distortions and how dislocations are able to move in the system1. A three-dimensional strong covalent network formed by carbon atoms makes diamond the hardest known material2. To overcome the limitation of diamond to ineffectively cut ferrous metals, dense TMBs with high boron content (e.g., OsB2, ReB2, CrB4, FeB4, MnB4)3,4,5,6,7,8,9 have been pursued. Implicit in such efforts is the assumption that dense TM atoms (creating high valence-electron density) prevent the structures from being squeezed while the high boron content (forming strong covalent B-B and TM-B network) withstands both elastic and plastic deformations, both of which enhance the hardness of materials. Amongst these TMBs, the highest boride of tungsten has currently become a focus of promising superhard materials because it combines ambient pressure synthesis, inexpensive raw materials with a measured superhardness (43.3–46.2 GPa under an applied load of 0.49 N)10,11,12,13,14,15,16,17. However, until recently, its structure has not been completely resolved. The heavy tungsten atoms hamper the accuracy to which the light boron atoms can be located by x-ray diffractions. Moreover, the versatile nature of boron atoms to form sp-, sp2- and sp3-hybridized bonds brings about the coexistence of various phases. These technological challenges result in the structural and compositional uncertainties. Combining first-principles calculations with thermodynamics, the long assumed WB4 phase18 has recently been determined as a simple and stoichiometric WB3 structure (called 2H)19. This conclusion has subsequently been substantiated by many theoretical and experimental studies20,21,22,23,24,25,26. On the other hand, agreement is far from complete for WB3. A theoretical study of WB3 has suggested that the 2H structure is incompatible with experimental results (e.g., superhardness, normalized c/a ratio) and that the question of the crystal structure of samples must be reopened27. In particular, an energetically more favorable WB3 (called 3R) has been proposed28. Hence, it is still unclear whether other phases are possible and what structural similarities may exist amongst these phases.
Since molybdenum is isoelectronic with tungsten, the crystal structure ambiguity for molybdenum borides is very much in parallel to that for tungsten borides. The highest boride of molybdenum was first reported as the MoB4 phase29 and later identified to be a triboride-based Mo1-xB3 structure30, but it was recently proposed31 that MoB4 should be the 2H-type MoB3. Meanwhile, the 3R-type MoB3 was theoretically presented32. It is therefore timely to elucidate the long-standing common mystery of this family of TMB3 and, in particular, to provide the essential guidance in the design of superhard materials.
Results
Polytypism in TMB3
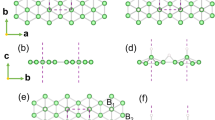
The 2H (3R) structure adopts hexagonal (rhombohedral) symmetry with space group P63/mmc (R-3m), in which boron and metal atoms locate at the Wyckoff 12i (18f) and 2b, 2c (6c) sites, respectively. As illustrated in Fig. 1, the boron atoms form planar graphitelike sheets (H). The metal atoms sit directly above the boron hexagons, skipping one column in every three, thus forming honeycomb metal layers (A). The B and C layers are actually identical to the A layer only displaced by one atom and two atoms, respectively. Accordingly, the stacking sequence AHBH (AHBHCH) well describes the 2H (3R) architecture and both consist of identical units of substructure (AH), piled one on top of the other in different numbers and in different stacking sequences within the unit cells.
Structures of boron and metal layers.
(a) Overlap view of hexagonal boron (H) and metal layers (A) along the [001] direction. (b) Side views of boron (H) and metal layers (A, B, C) along the [110] direction. The honeycomb metal layer (A) can be derived from a close-packed metal layer by removing one third of the metal atoms (marked by the red plus sign “+”) and the B and C layers are actually identical to the A layer only shifted by translations of (2a/3, a/3) and (a/3, 2a/3), respectively. Here a is the lattice constant of its unit cell (shown by the black dashed lines). The small (green) and large (blue) spheres represent the boron and metal atoms, respectively.
Superhard TMBs have long been believed to exist only in simple crystal structures, similar to 2H, 3R or other structure types, following the general idea in the design of superhard materials2,3,4. However, on the basis of the structure stacking principle mentioned above, we may reasonably infer that a very large number of polytypic structural modifications of TMB3 can be built up using alternating metal and boron layers by systematically specifying the stacking sequence of metal layers. In these architectures, the stacking sequences of boron layers are completely the same. The differences amongst various structures, however, lie in the stacking sequences of metal layers. For the case with two metal layers in the unit cell, the only two stacking sequences (AB and AC) yield an equivalent hexagonal structure that is none other than the experimentally observed 2H form25. Likewise, three metal layers comprise two orders (ABC and ACB) that produce a same rhombohedral framework. This framework is exactly the theoretically uncovered 3R structure28,32. For four metal layers, the four stacking sequences (ABAC, ABCB, ACAB and ACBC) equivalently create a previously unreported hexagonal configuration (called 4H). A complete list of previously unidentified structures (called 5H, 6H1, 6H2, 7H1, 7H2, 7H3, 8H1, 8H2, 8H3, 8H4, 8H5 and 8H6) comprising 5–8 metal layers in their unit cells can be constructed. In general, the TMB3 crystals could be imagined to display one-dimensional disordered stacking of metal layers along the [001] direction. Therefore, polytypism is revealed to be the extra hidden degree of freedom in the structure design of superhard WB3 and MoB3 with a large number of polytypes due to the different stacking of metal layers amongst the interlocking boron layers.
Stability of TMB3 polytypes
The thermodynamic stability of all those TMB3 polytypes can be firmly proved for their viability from first-principles calculations (see Supplementary Information for details). Based on that, our work is able to systematically identify a set of new configurations that are energetically more favorable than the experimentally observed but metastable 2H structure. The calculated formation energies of fifteen TMB3 polytypes are summarized in Fig. 2. In addition to the concrete values, the relative stability of different polytypes for WB3 and MoB3 has main features in common. The formation energy of the 2H structure is found to be the highest amongst the TMB3 polytypes considered, though it is still negative (−1.185 eV/f.u. for WB3 or −1.256 eV/f.u. for MoB3). This makes the 2H structure metastable but thermodynamically viable, which supports the experimental observation25. Amongst these polytypes, the 3R type has the lowest formation energy (−1.222 eV/f.u. for WB3 or −1.283 eV/f.u. for MoB3) and becomes the ground state of TMB3. Hence, the 2H and 3R structures are the extremes in formation energy governing the thermodynamic stability of these polytypes. It is interesting to note that the energy differences amongst polytypes are extremely small and the maximum separation is as low as 0.037 eV/f.u. for WB3 and 0.027 eV/f.u. for MoB3. Considering the temperature effect on formation energy, such a small energy difference manifests polytypism in TMB3 with a large class of energetically degenerate structures.
Formation energy versus the number of metal layers within the unit cell for (a) WB3 and (b) MoB3 polytypes.
The formation energy, defined as ΔE = E(TMB3) − E(TM) − 3E(B), is obtained from the first-principles calculations, referring to W and Mo in body-centered cubic phases and to B in α-B phase as their respective ground states. The red and black dashed lines indicate the lowest and highest energy values, with an energy distribution width as small as 37 meV (27 meV) per WB3 (MoB3) formula unit (f.u.), amongst all the calculated polytypes.
As a matter of fact, the newly identified TMB3 structures can be envisaged as different mixtures of the 2H and 3R ones. In these layered crystals, the metal layers can be considered as being held together by the boron layers. In contrast to the classic layered materials (e.g., graphite, h-BN) that are characterized by weak interlayer interactions (e.g., Van der Waals), TMB3 are dominated by strong intralayer B-B and interlayer TM-B covalent bonds22,28. Stacking faults between the adjacent metal layers, say between AHB and AHC, basically do not alter the local environments of B-B and TM-B interactions and the energy difference amongst different stackings is very small. Hence, stacking faults, resulting from the intrinsic short-range behavior of strong covalent bonds, play a decisive role in the occurrence of polytypism in TMB3.
The dynamic lattice stability of TMB3 polytypes can also be supported through their phonon dispersion. For the 2H and 3R structures, the calculated phonon dispersion curves show no imaginary frequencies throughout the whole Brillouin zones, confirming the dynamic stability of both basic structures. Since other polytypes are viewed as different mixtures of 2H and 3R, the TMB3 polytypes are deemed dynamically stable (see Supplementary Information for details).
Based on the published XRD patterns11,25 of the experimental samples, only the 2H structure can agree with them, since others polytypes cannot avoid introducing apparent additional peaks generated by tungsten layer which obviously disagrees with the experimental patterns. Although the newly identified structures are metastable with respect to the ground-state 3R phase, they are energetically more favorable than the experimentally synthesized 2H structure and are dynamically stable. Moreover, as mentioned above, the energy differences amongst various polytypes are extremely small. Considering the temperature effect, the newly identified TMB3 polytypes should be viable. The temperature-dependent Gibbs free energies derived by Cheng et al.25 has revealed that the 2H phase becomes more stable than the 3R phase above 659 K within the GGA method (above 678 K within the LDA method), which explains why the ground-state 3R phase has never been observed. Therefore, these results provide an extremely useful indication that the polytypic TMB3 structures should be synthesized under appropriate conditions (e.g., at proper temperatures).
Mechanical properties of TMB3 polytypes
We also evaluate the influence of different polytypic structures on mechanical properties of TMB3. The obtained bulk modulus, shear modulus and Vickers hardness for fifteen TMB3 structures are displayed in Fig. 3. The overall trends are very similar, even though mechanical properties of MoB3 are slightly inferior to those of WB3. Interestingly, their mechanical properties are hardly affected by the number of metal layers in their unit cells and the differences amongst various polytypic structures are also very small. In particular, the estimated hardness values (38.0–38.9 GPa for WB3 or 36.1–37 GPa for MoB3) do not change much from the calculated data with the range of only 1 GPa, regardless of the polytypes stacking sequence. The results demonstrated that the intrinsic hardness of the TMB3 polytypes mainly depends on the interaction between metal and boron layers. In these layered TMB3 structures, the interlayer TM-B bonds are relatively weaker than the intralayer B-B bonds, although they are also strong bonds. This allows the layers to cleave readily under a large shear stress. It was verified by a theoretical study of the 2H structure that has the lowest indentation shear strength along the [110] direction under the (001) plane27. Therefore, the sliding strength between layers largely limits the intrinsic hardness enhancement of the TMB3 polytypes.
To further enhance the hardness, the relatively easy sliding of the layers under the large shear stress must be suppressed. As mentioned above, TMB3 can form a variety of polytypic structures. Moreover, these structures have the nearly same energies. We thus propose that one can create a multiphase solid-solution compound with the coexistence of various polytypes. This particular material may include a large number of interfaces amongst different polytypic structures with different easy sliding directions and these interfaces would strongly hinder the interlayer sliding movement of each polytype, accordingly allowing the possibility of an extrinsic hardness enhancement. A recent experiment15 showed that a greatly enhanced hardness was achieved when pure metals (e.g., Ta, Mn, Cr) were added to WB3. In contrast to this traditional solid-solution of different compositional substances, the hardening way by creating a multiphase compound with various polytypes to restrict the propagation of dislocations does not change the chemical compositions of materials. Moreover, this mechanism is expected to be applicable to other systems. As a matter of fact, the ultrahigh strength (hardness) of the recently synthesized nano-twin Cu (c-BN) samples33,34 has already corroborated this. The nature of strengthening is the effective blockage of dislocation motion by numerous coherent boundaries, although the practical approaches of creating grain boundaries are different.
Thermal conductivity of TMB3 polytypes
Such a class of special superhard materials own ultra-low thermal transport capability, completely opposite to the conventional knowledge that intrinsically strong chemical bonds in superhard materials would lead to high lattice thermal conductivity due to the inherently high bulk moduli and sound velocities. The polytypism in TMB3 greatly influences lattice thermal conductivity κL along the [001] direction. As well understood, the acoustic part of phonons carries most of the heat in a material. The out-of-phase vibrations from a large number of randomly distributed atoms within the polytypism-enlarged unit cell, together with the inherently polytypism-induced interfaces, strongly scatter heat-carrying phonons. Meanwhile, as the number of metal layers in the unit cell increases, the Brillouin zone keeps “folding-in” and the Debye temperatures ΘD and Debye frequencies ωD of acoustic phonon modes decrease correspondingly35. Figure 4(a) plots the phonon dispersions along the [001] direction for the 2H and 4H structures of WB3. Since the Brillouin zone of 4H in this direction becomes smaller, the acoustic modes “hit” the Brillouin zone boundary much earlier than the phonons in 2H. Hence, ωDs are greatly reduced from 4.4 THz and 3.8 THz for 2H to 2.7 THz and 2.0 THz for 4H for the longitudinal acoustic mode (LA) and transverse acoustic mode (TA), respectively. On the other hand, the sound velocities (5180 m/s and 6900 m/s) and Grüneisen parameters (1.37 and 1.74) for the TA and LA modes remain almost the same amongst the 2H, 3R, 4H and 5H polytypes. Given these parameters, the lattice thermal conductivity κL could be estimated via the Debye-Callaway method36. The room temperature κL along the [001] direction with respect to the number of atoms in the unit cell is plotted in Fig. 4(b). It can be observed that κL decreases with increasing number of the random stacking layers, primarily due to the reduced Debye frequencies or Debye temperatures. Very low κL close to minimal might be achieved after several repetitions of units. Such unusual ultra-low lattice thermal conductivity of TMB3 is very unique and could be extremely useful in particular applications, such as one-dimensional thermal barrier with superhardness.
In summary, we show that polytypism exists in superhard WB3 and MoB3 with a large number of energetically degenerate structures due to the different stacking of metal layers amongst the interlocking boron layers. Although all the polytypic structures have nearly equivalently intrinsic hardness, such polytypism may create a multiphase solid-solution compound with a large number of interfaces amongst different polytypes and these interfaces will strongly suppress the interlayer sliding movement of each polytype, accordingly allowing the possibility of an extrinsic hardness enhancement. Furthermore, the polytypic TMB3 manifest extremely low lattice thermal conductivity due to structural disorders and phonon folding. Our findings shed light on the structure design of superhard materials and, at the same time, provide a new strategy in the search for superhard materials with additional functionalities.
Methods
Calculations on the basis of the density functional theory were carried out with the Vienna Ab initio Simulation Package (VASP) code37 and the electron-ion interactions are described by means of projector augmented wave (PAW) with 5d46s2 (4d45s2) and 2s22p1 electrons as valence for W (Mo) and B, respectively. The exchange-correlation functional within the generalized gradient approximation (GGA)38 were employed. Because of the extremely small energy difference amongst different structures, a large cutoff energy of 500 eV and dense Monkhorst-Pack k-point meshes with a grid of 0.02 Å−1 for Brillouin zone samplings were adopted to ensure the numerical convergence of formation energy differences to typically 1 meV/atom.
Having fully optimized fifteen specific polytypic structures for TMB3, their formation energies (ΔE) at temperature T = 0 K were calculated. Bulk modulus (B) and shear modulus (G) are determined by the efficient strain energy method39 while the intrinsic Vickers' hardness is estimated by Chen's model [H = 2(k2G)0.585 − 3, k = G/B]40,41. Also, the phonon dispersion curves and lattice thermal conductivities along the [001] direction for the 2H, 3R, 4H and 5H structures in WB3 and MoB3 were calculated. (see Supplementary Information for details).
References
Hugosson, H. W., Jansson, U., Johansson, B. & Eriksson, O. Restricting dislocation movement in transition metal carbides by phase stability tuning. Science 293, 2434–2437 (2001).
Kaner, R. B., Gilman, J. J. & Tolbert, S. H. Designing superhard materials. Science 308, 1268–1269 (2005).
Cumberland, R. W. et al. Osmium diboride, an ultra-Incompressible hard material. J. Am. Chem. Soc. 127, 7264–7265 (2005).
Chung, H. Y. et al. Synthesis of ultra-incompressible superhard rhenium diboride at ambient pressure. Science 316, 436–439 (2007).
Niu, H. et al. Structure, bonding and possible superhardness of CrB4 . Phys. Rev. B 85, 144116 (2012).
Knappschneider, A. et al. Possible superhardness of CrB4 . Inorg. Chem. 52, 540–542 (2013).
Gou, H. et al. Discovery of a superhard iron tetraboride superconductor. Phys. Rev. Lett. 111, 157002 (2013).
Knappschneider, A. et al. Peierls-distorted monoclinic MnB4 with a Mn-Mn bond. Angew. Chem. Int. Ed. 53, 1684–1688 (2014).
Gou, H. et al. Peierls distortion, magnetism and high hardness of manganese tetraboride. Phys. Rev. B 89, 064108 (2014).
Gu, Q., Krauss, G. & Steurer, W. Transition metal borides: Superhard versus ultra-incompressible. Adv. Mater. 20, 3620–3626 (2008).
Mohammadi, R. et al. Tungsten tetraboride, an inexpensive superhard material. Proc. Natl. Acad. Sci. U.S.A. 108, 10958–10962 (2011).
Rau, J. V. et al. Superhard tungsten tetraboride films prepared by pulsed laser deposition method. ACS Appl. Mater. Inter. 3, 3738–3743 (2011).
Liu, C. J. et al. Low-compressibility of tungsten tetraboride: a high pressure X-ray diffraction study. High Press. Res. 31, 275–282 (2011).
Xie, M. et al. Exploring the high-pressure behavior of superhard tungsten tetraboride. Phys. Rev. B 85, 064118 (2012).
Mohammadi, R. et al. Toward inexpensive superhard materials: tungsten tetraboride-based solid solutions. J. Am. Chem. Soc. 134, 20660–20668 (2012).
Xiong, L. et al. Radial x-ray diffraction of tungsten tetraboride to 86 GPa under nonhydrostatic compression. J. Appl. Phys. 113, 033505 (2013).
Wang, M., Li, Y., Cui, T., Ma, Y. & Zou, G. Origin of hardness in WB4 and its implications for ReB4, TaB4, MoB4, TcB4 and OsB4 . Appl. Phys. Lett. 93, 101905 (2008).
Romans, P. A. & Krug, M. P. Composition and crystallographic data for the highest boride of tungsten. Acta Cryst. 20, 313–315 (1966).
Liang, Y., Yuan, X. & Zhang, W. Thermodynamic identification of tungsten borides. Phys. Rev. B 83, 220102(R) (2011).
Gou, H., Li, Z., Wang, L., Lian, J. & Wang, Y. Peculiar structure and tensile strength of WB4: nonstoichiometric origin. AIP Adv. 2, 012171 (2012).
Zhang, R. F. et al. Stability and strength of transition-metal tetraborides and triborides. Phys. Rev. Lett. 108, 255502 (2012).
Liang, Y. et al. An unexpected softening from WB3 to WB4 . Europhys. Lett. 98, 66004 (2012).
Liang, Y., Zhong, Z. & Zhang, W. A thermodynamic criterion for designing superhard transition-metal borides with ultimate boron content. Comp. Mater. Sci. 68, 222–228 (2013).
Li, Q., Zhou, D., Zheng, W., Ma, Y. & Chen, C. Global structural optimization of tungsten borides. Phys. Rev. Lett. 110, 136403 (2013).
Cheng, X. et al. Interstitial-boron solution strengthened WB3 + x . Appl. Phys. Lett. 103, 17193 (2013).
Cheng, X. Y., Chen, X. Q., Li, D. Z. & Li, Y. Y. Computational materials discovery: the case of the W-B system. Acta Cryst. C 70, 85–103 (2014).
Zang, C., Sun, H. & Chen, C. Unexpectedly low indentation strength of WB3 and MoB3 from first principles. Phys. Rev. B 86, 180101(R) (2012).
Liang, Y., Gou, Y., Yuan, X., Zhong, Z. & Zhang, W. Unexpectedly hard and highly stable WB3 with a noncompact structure. Chem. Phys. Lett. 580, 48–52 (2013).
Chetien, A. & Helgorsky, J. Borides of molybdenum and tungsten, MoB4 and WB4, new compounds. Compt. Rend. Acad. Sci. 252, 742–744 (1961).
Lundstrom, T. & Rosenberg, I. The crystal structure of the molybdenum boride Mo1-xB3 . J. Solid State Chem. 6, 299–305 (1973).
Liang, Y., Yuan, X., Fu, Z., Li, Y. & Zhong, Z. An unusual variation of stability and hardness in molybdenum borides. Appl. Phys. Lett. 101, 181908 (2012).
Zhang, M., Wang, H., Wang, H., Cui, T. & Ma, Y. Structural modifications and mechanical properties of molybdenum borides from first principles. J. Phys. Chem. C 114, 6722–6725 (2010).
Lu, L., Shen, Y., Chen, X., Qian, L. & Lu, K. Ultrahigh strength and high electrical conductivity in copper. Science 304, 422–426 (2004).
Tian, Y. et al. Ultrahard nanotwinned cubic boron nitride. Nature 493, 385–388 (2013).
Toberer, E. S., Zevalkink, A. & Snyder, G. J. Phonon engineering through crystal chemistry. J. Mater. Chem. 21, 15843–15852 (2011).
Zhang, Y. et al. First-principles description of anomalously low lattice thermal conductivity in thermoelectric Cu-Sb-Se ternary semiconductors. Phys. Rev. B 85, 054306 (2012).
Kresse, G. & Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. A 65, 349–354 (1952).
Chen, X. Q., Niu, H., Li, D. & Li, Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 19, 1275–1281 (2011).
Niu, H. et al. Extra-electron induced covalent strengthening and generalization of intrinsic ductile-to-brittle criterion. Sci. Rep. 2, 718 (2012).
Acknowledgements
We acknowledge the financial support from the National Natural Science Foundation of China (No.51072213, 11234012, 51121064), State Oceanic Administration (No.SHME2013JS01) and the Local Colleges Faculty Construction (No.11160501000) and the Basic Research Field (No. 11JC1404700, 13JC1402900, 14XD1424300) for Science and Technology Commission of Shanghai Municipality. The team members at the University of Washington would like to acknowledge the financial support from the US Department of Energy under corporate agreement DE-FC26-04NT42278, GM, National Science Foundation under award number 1235535 and the Kyocera Corporation.
Author information
Authors and Affiliations
Contributions
W.Q.Z. and Y.C.L. conceived the project; Y.C.L., J.Y., X.Y. and W.J.Q. performed theoretical calculations; Y.C.L., J.Y., X.Y., W.J.Q., Z.Z., J.H.Y. and W.Q.Z. analyzed results; Y.C.L., J.Y., W.Q.Z. and J.H.Y. wrote the paper. All contributed to the discussion of the results.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. The images in this article are included in the article's Creative Commons license, unless indicated otherwise in the image credit; if the image is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the image. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Liang, Y., Yang, J., Yuan, X. et al. Polytypism in superhard transition-metal triborides. Sci Rep 4, 5063 (2014). https://doi.org/10.1038/srep05063
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep05063
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.