Introduction

Stimulated Brillouin Scattering (SBS), whereby light interacts coherently with acoustic phonons, is one of the strongest nonlinear effects observed in optical fibres1,2,3. In the SBS process, a narrow-band pump field of frequency ω0 can generate a strong backward-propagating Stokes field of frequency ω1 = ω0 − ΩB through interaction with acoustic phonons (frequency ΩB) once a certain power threshold is reached. Although SBS in optical fibres can be detrimental to optical systems, it has also enabled a range of important technologies such as Brillouin fibre lasers4,5,6, amplifiers2, sensors7, pulse compressors8, phase conjugators9, as well as devices for slow light10,11,12, stored light13, laser cooling of vibrational modes14, low phase-noise microwave oscillators15 and all-optical signal processing16,17.

Brillouin lasing is achieved by generating Stokes photons via SBS in a cavity4,5,6. Due to the cavity feedback, the power threshold for the generation of the Stokes waves is reduced considerably18. The linewidth of the Stokes field can then be much narrower than the Brillouin gain bandwidth ΔvB = 1/(2πτ), where τ is the phonon lifetime3. In Brillouin lasers with short cavities, i.e. cavities short enough such that the free spectral range (FSR) of the cavity is of the order of the gain bandwidth ΔvB, only one cavity mode experiences strong Brillouin gain. Such lasers emit a single frequency Stokes wave once the lasing threshold is reached. In the general (off-resonant) case, the peak of the SBS gain spectrum (ω0 − ΩB) does not coincide with a cavity resonance and the frequency of the Stokes wave ω1 is determined by an interplay between Brillouin gain, nonlinear phase-shift from the Kerr-nonlinearity and cavity selectivity, known as Stokes detuning19.

SBS can be cascaded in resonators, which produces multiple, frequency shifted Stokes waves, thus forming a Brillouin frequency comb20. The spectral lines of BFCs are spaced by the Brillouin frequency shift ΩB which is determined by the acoustic properties of the medium (ΩB/2π ≈ 10 GHz for glasses) and is independent of the resonator length. BFCs have been demonstrated in different configuration, such as Fabry-Perot cavities18,20, phase-conjugate resonators21, fibre ring cavities22, Brillouin-erbium fibre lasers23 and micro-resonators6,15,24. Phase-locking of such combs holds a promise to achieve pulsed laser sources with gigahertz repetition rates25,26. This is orders of magnitude larger than the repetition rates of conventional passively mode-locked fibre lasers which are fundamentally linked to the laser cavity length and therefore are typically of the order of 10–100 megahertz27.

In the absence of any additional nonlinear effect than SBS, phase-locking of BFCs can only be achieved by coupling all Stokes waves with a common acoustic wave. Yet, in resonators with a single optical transverse mode, acoustic waves that couple adjacent comb components have different propagation constants19,28. Coupling multiple Stokes waves with a single acoustic wave is thus problematic: the interaction is not phase-matched and becomes inefficient over distances greater than a few millimeters25. In resonators that allow SBS interaction over longer lengths, each Stokes wave is formed through stimulated scattering from a new acoustic wave. In this process, the Stokes waves attain random phases as each acoustic wave grows from noise29. In addition, phase-noise and unequally spaced comb components, due to different detunings of the Stokes waves, lead to a changing spectral phase of the BFC with time.

Different cavity configurations have been suggested to achieve phase-locking of BFCs21,25,26,30. Experimentally, phase-locking of BFCs has been demonstrated by achieving coupling of all Stokes waves with a common acoustic wave by limiting the SBS interaction to a short part of the cavity21 and by using modal dispersion in a short-multimode fibre30. Recently, an autocorrelation measurement of a Brillouin comb generated in a Brillouin-erbium fibre laser has been presented that suggests pulse-like behaviour in the time domain31. However, the phase-locking mechanism for this configuration has not been explained and the autocorrelation presented is not unambiguous evidence of a pulse train due to a relatively large autocorrelation background32.

Kerr-induced four wave-mixing (FWM) also leads to generation of new frequencies and, unlike SBS, is known to couple three or more optical waves in a phase-sensitive manner3,33. It has been shown that frequency combs generated through cascaded FWM in high-finesse micro-resonators can exhibit certain spectral phase signatures34. Recently, phase-locking and generation of temporal solitons have also been observed in such a configuration35.

In resonators, SBS and FWM can efficiently co-exist. Degenerate FWM between co-propagating pump and Stokes waves (generated via SBS) create Anti-Stokes waves at frequencies ωj = ω0 − j × ΩB, for j < 0 and higher-order Stokes waves at frequencies ωj = ω0 − j × ΩB for j ≥ 2. Generation of Anti-Stokes waves is a clear sign of the presence of FWM since these waves cannot be generated by SBS. The Stokes waves generated via FWM, in turn, can act as a seed and can be further amplified by SBS, thus reducing the threshold for higher-order Stokes waves36,37,38,39. Steady state powers of Stokes and anti-Stokes waves formed by the interplay of SBS and FWM in a Fabry-Perot cavity have previously been studied theoretically40, however in this earlier study the authors were only interested in the time-averaged steady state powers and the phase-relationship between the waves was not considered.

In this work, we demonstrate for the first time numerical and experimental results that show the generation of phase-locked BFCs with repeatable spectral phase via the interplay of SBS and FWM. Real-time measurements of the comb show stable picosecond pulse trains with GHz repetition rate. Our experiment was performed in a short (~38 cm), low finesse, Fabry-Perot fibre cavity. A detailed numerical study of the system shows good agreement with experimental results and clearly establishes that FWM is essential for the system's dynamics to attain a phase-locked steady state.

This new understanding of the interaction between FWM and SBS can potentially be exploited for creating novel picosecond pulse sources with GHz repetition rate for optical communication systems, metrology and high speed optical clocks41.

Results

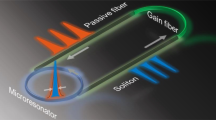
BFCs were generated by coupling quasi-continuous wave (quasi-CW) pump light into a Fabry-Perot cavity consisting of a short piece of As2Se3 chalcogenide glass42 fibre as illustrated schematically in Fig. 1. Quasi-CW light was used to avoid thermal effects by keeping the average power low (~10 mW) while obtaining high peak powers (~1 W). The pump light consisted of narrow band 500 ns square pulses at 1550 nm. The polarisation of the pump was adjusted such that only one polarisation mode was excited. Due to a large refractive index of n = 2.81, the Fresnel reflections on the perpendicularly cleaved fibre facets provided feedback of about R = 22.6%. A single transverse mode with an effective area of Aeff = 56 μm2 was guided by the fibre. The large Brillouin gain43,44gB = 6.10 × 10−9 m/W and nonlinear refractive index45n2 = 2.4 × 10−13 cm2/W of the chalcogenide glass allowed us to perform the experiment in a short fibre length L = 38.29 cm. The phonon lifetime43 in As2Se3 is τ = 1/(2πΔv) = 12 ns. The Brillouin frequency shift and the FSR of the fibre cavity were measured to be ΩB/(2π) = 7.805 GHz and FSR = 139.3 MHz, respectively. The fibre length L was chosen such that it was long enough to allow generation of cascaded Stokes waves via SBS at peak intensities well below the damage threshold of As2Se3 and to be short enough that only one cavity mode experiences strong Brillouin gain (FSR > Δv). The linear propagation loss of the As2Se3 fibre43 is α = 0.84 dB/m and the dispersion coefficient42 is about D = −504 ps km−1nm−1. Details about the experimental setup can be found in the Methods section.

Figure 1
figure 1

Concept of pulse train generation via SBS and FWM.

CW light is coupled into a short, nonlinear fibre resonator. New frequencies are generated via SBS and FWM. At the output a train of phase-locked pulses can be observed with repetition rate equal to the SBS frequency shift.

Full size image

Important parameters of the system dynamics40 are the linear phase-shift Δφj, of the pump (j = 0) and Stokes waves (j = 1,2,..) per cavity roundtrip. It is convenient to describe these linear phase shifts in the form

where Δφ0 = 2ω0nL/c is the linear phase shift of the pump per round trip and β = 2ΩBnL/c is the difference of the linear phase shifts of the two adjacent comb components per round trip (without Stokes detuning). Here, we neglected the dispersion of the effective index n and the Brillouin shift ΩB because we only consider a small frequency range (~30 GHz). Since Δφ0 represents an absolute phase, it is sensitive to small changes of n and L due to temperature drift of the cavity and also to tuning the frequency ω0 of the pump laser. In the experiment Δφ0 has not been stabilised and its values are unknown. The parameter β is a phase-difference and is far less sensitive to pump tuning and temperature drift than Δφ0 and is assumed to be constant in the parameter range considered here. For both experiments and simulations, β was a multiple of 2π. However, we found that this is not the only condition for observing phase-locking and qualitatively similar results were also obtained in experiments and simulations for different values of β.

Experiment

Figure 2(a) shows the optical spectrum of the input light. The spectrum consists of a single line at λ = 1550.2 nm corresponding to the pump light (P). A time domain measurement of the input light is plotted in the inset in Fig. 2(a), showing a square pulse of 500 ns length with a slight slope decreasing toward the end of the pulse arising from the amplification process. A typical spectrum measured at the output of the chalcogenide fibre for about 0.7 W peak power coupled into the fibre is plotted in Fig. 2(b). Besides the pump light (P) the output spectrum also exhibits three Stokes lines at longer wavelength (1S–3S) and two anti-Stokes waves (1AS, 2AS) at shorter wavelengths compared to the pump (P). The Stokes waves (1S–3S) were generated through the interplay of SBS and FWM and the anti-Stokes waves (1AS, 2AS) were generated through FWM of pump and Stokes waves18,46. The spacing between two neighboring lines is about Δλ = 63 pm, which is equal to the SBS frequency shift of the As2Se fibre Δλ = ΩBλ2/(2πc) at λ = 1550 nm.

Figure 2
figure 2

Optical spectra of input and output light of the fibre resonator.

(a) Spectrum of the input light consisting of a single pump frequency (P). The inset shows the temporal measurement of a 500 ns input pulse. (b) Averaged output spectrum of the fibre resonator for about 0.7 W input peak power. Besides the pump (P), Stokes waves (1S–3S) at longer wavelength as well as anti-Stokes waves (1AS, 2AS) at shorter wavelengths are visible.

Full size image

Two real-time measurements of output light from the chalcogenide fibre cavity are shown in Fig. 3(a) and 3(b) for the input powers of about 0.7 W but for different values of Δφ0. Recall that the phase shift Δφ0 could be changed by tuning the frequency ω0 of the pump laser. The insets to (a) and (b) show zoomed-in sections of 1 ns time intervals of the main graph. Compared to the input quasi-CW pulses, the output pulses show rapid temporal interference signals after about 25 ns which are not resolved in the main graph. The inset at about 30 ns in Fig. 3(a) reveals a cosine oscillation, which we attribute to beating between the pump and the newly generated first Stokes wave3,28. The frequency of the beat signal corresponds to ΩB/(2π), i.e. the Brillouin frequency shift.

Figure 3
figure 3

Temporal measurements of output pulses.

(a), (b) Output pulses of the fibre resonator for 500 ns input pulses for two different values of the phase-shift Δϕ0. The insets show zoomed in sections of 1 ns length at different times. Both measurements were taken for similar input powers of ~0.7 W.

Full size image

We first consider envelopes of the interference signals in Fig. 3(a) and 3(b). In Fig. 3(a) the envelope of the interference signal is modulated with a period of approximately 100 ns, whereas a constant envelope of the interference signal can be seen in Fig. 3(b). The two insets (at 246 ns and 373 ns) in Fig. 3(a) reveal a strong second frequency of 2×ΩB/(2π). The spectrum shown in Fig. 2(b) suggests that the main contribution to this higher frequency is a result of interference between the pump and second-order Stokes wave. It is clear from the insets that the interference signal of the multiple waves in Fig. 3(a) is not constant throughout the 500 ns pump duration and that the phase-relationship of the waves drifts in time (at the rate of approximately 1/100 ns = 10 MHz). This drift arises from non-equally-spaced comb lines resulting from different Stokes detunings of the first and second-order Stokes waves.

Figure 3(b) shows a qualitatively different result obtained for a different value of Δφ0. After about 100 ns the system reaches a steady state with a constant envelope of the modulation. The zoomed-in sections of the interference signal, shown in the insets at 200 ns and 400 ns reveal a stable train of ~40 ps sub-pulses with a repetition rate of ~ΩB/(2π). The pulse shape is the result of the interference of at least 3 waves (such as pump, first and second-order Stokes wave) equally spaced in frequency and with a constant phase relationship.

This phase-locked train of pulses is repeatable and stable if the experiment is repeated with the same experimental conditions. We demonstrated this by recording the output pulses for a series of input pump pulses. Figure 4(a) shows 11 output pulses observed for 11 independent 500 ns input pulses coupled into the fibre with 0.5 ms delay between the pulses. All output pulses display very similar temporal behavior. Figure 4(b) shows a 0.5 ns long zoomed-in section of the output pulses at 325 ns, revealing the same interference of the waves for all traces. From this we conclude that the waves that contribute the interference have the same phase-relationship for all measurements.

Figure 4
figure 4

Temporal stability.

Temporal measurements of a series of eleven independent output pulses recorded in a 5 ms time interval with 0.5 ms time separation between the measurements. (a) Showing the entire 500 ns output pulses. (b) 0.5 ns long zoomed-in section of the pulses shown in (a) at 325 ns. (The maxima are aligned for better visibility.)

Full size image

Numerical study

The experiment indicates that a stable train of pulses can be obtained with a phase-relationship of the contributing waves, which is repeatable and constant in time. As outlined above, SBS alone does not possess a mechanism to provide either of these properties.

We believe that FWM can explain phase-locking with a repeatable phase-relationship. We demonstrated this by performing a numerical study of the system with and without FWM and compared the simulation results. For the sake of simplicity we only present results for the smallest number of waves that are necessary to qualitatively reproduce the experimental results in this paper and to demonstrate the phase-locking mechanism.

The model includes forward and backward propagating pump, first and second-order Stokes waves and the corresponding four acoustic waves which couple these waves in a fibre oriented along the z-direction. The interaction between these six optical and four acoustic waves can be described in terms of the dynamic coupled mode-equations19 (S3)–(S7) shown in the Supplementary Information. In these equations we included terms relevant to the SBS interaction, as well as the effects arising from the Kerr-nonlinearity: self-phase modulation (SPM), cross-phase modulation (XPM) and FWM. Simulation parameters were chosen to match experimental conditions. The boundary conditions used in the simulation are given in equations (S8) in the Supplementary Information. Reflections from the facets of the fibre cavity and the linear phase-shifts of pump and Stokes waves per cavity roundtrip described by Δϕj (see equation (1)) have been considered. Information on how the coupled mode-equations were integrated can be found in the Methods section.

To compare simulation and experimental results we look at the optical power at the output of the fibre. The optical (pump (j = 0), first (j = 1) and second (j = 2) Stokes) waves in the fibre resonator can be described in terms of the complex amplitudes of their electric fields:

Here “±” indicates the direction of propagation, are the slowly varying complex envelopes of the amplitudes . represent the phases of the waves, n ≈ 2.81 is the effective index and ωj are the steady state frequencies of the waves. We assume that the complex amplitudes are normalized such that represent the optical powers of the waves measured in dimensions of Watts. The output power Pout(t) at the end of the fibre resonator can be calculated with

In order to obtain stable pulses at the output of the fibre, the powers and the phases must attain a steady state. The total output power Pout(t) in the steady state can be calculated by inserting equation (2) into equation (3) to yield

where is a constant time offset. In Equation (4) we have introduced the phase parameter

ϑ±(z,t) express the phase relationships between the three forward and backward propagating electric fields and , respectively. The values of ϑ±(z,t) are critical for the phase-sensitive FWM interaction between the waves33. Depending on the phase-relationships ϑ±(z,t), power flows from the first Stokes to the pump and the second Stokes or the other way around. Furthermore, the sign and the magnitude of nonlinear phase-shifts caused by FWM depend on ϑ±(z,t) (see Supplementary Information equations (S10–S15)). Equation (5) shows that even when the powers and the phases are independent of time, ϑ+(L,t) drifts with a constant rate if the frequencies ωj are not equally spaced, preventing a stable interference signal Pout(t). The steady state frequencies ω1 and ω2 of the Stokes waves are determined by a complicated interplay of Brillouin gain, nonlinear phase-shift from the Kerr-nonlinearity and cavity selectivity. In general, different order Stokes waves experience different amounts of Stokes detuning and the frequencies of the three waves are not equally spaced. Additionally, in order to obtain short pulses (of length ~2π/(NΩB), where N is the number of participating waves26), ϑ+(L,t) must also be close to zero to achieve the appropriate phasing of the three waves.

To illustrate the effect of FWM we first performed the simulations with and without FWM interaction while the terms for SBS, SPM and XPM remained in the equations.

Figure 5(a) and 5(b) show two qualitatively different results that were obtained by including FWM in the simulation, consistent with experimental conditions. Both simulations were performed using the estimated coupled input power of the experiment Pin = 0.7 W. For the parameter Δφ0 we choose Δφ0 = 0.548 π and Δφ0 = 1.2 π, respectively, in order to obtain results that are qualitatively similar to the experimental results shown in Fig. 3(a) and 3(b). The plots on the left show the evolution of the powers and the phase parameter ϑ+(L,t) whereas the plots on the right display the output power of the fibre Pout(t). The insets of the plots on the right show 1 ns long zoomed-in sections at different times. In Fig. 5(a) (Δφ0 = 1.2 π) neither the powers nor the parameter ϑ+(L,t) reach a steady state so the envelope of the burst is modulated and the pulses are not stable. However, for Δφ0 = 0.548 π in Fig. 5(b) the phase parameter ϑ+(L,t) and the powers reach a steady state after an initial power transfer from pump to the Stokes waves. Since the powers and ϑ+(L,t) are independent of time, a stable train of pulses can be obtained.

Figure 5
figure 5

Simulation Results with and without FWM interaction.

Left: Computed temporal evolution of the powers of pump, first and second-order Stokes wave and the phase parameter ϑ+(L,t) at the end of the fibre for input power Pin = 0.7 W. Right: Total output power Pout(t). (a) FWM included in the simulation, Δφ0 = 1.2 π. (b) FWM included in the simulation, Δφ0 = 0.548 π. (c) FWM not included in the simulation, Δφ0 = 0.548 π.

Full size image

Figure 5(c) shows simulation results obtained when FWM was not included in the simulation. The same parameters were used that generated the results of Fig. 5(b) (Pin = 0.7 W, Δφ0 = 0.548 π). After an initial power transfer to the Stokes waves, the powers of all waves reach a steady state3,28. However, ϑ+(L,t) drifts at a constant rate, which is the result of unequally spaced frequencies. Since ϑ+(L,t) is not constant the interference signal changes with time and has a modulated envelope (Fig. 5(c), right).

The results of the simulation demonstrate that FWM links the parameter ϑ±(z,t) to the powers and vice versa. This important contribution of FWM is also illustrated by the steady state equations (S10)–(S15) shown in the Supplementary Information. The FWM terms (and only these terms) contain the phase parameters ϑ±(z,t). From the steady state equations it follows that ϑ±(z,t) must be time-independent, leading to the condition of phase-locking between the three waves. Furthermore, FWM couples the steady state powers to the phases and also the phases to each other via terms containing the phase parameters ϑ±(z,t). In the absence of FWM the steady state powers are independent of the phases as in a simple Brillouin laser configuration19. Thus, FWM is crucial to establishing a phase-locked output in the steady state.

In order to generalize these simulation results for a larger parameter space, we performed a two dimensional parameter scan. We chose to scan the input power Pin and the parameter Δφ0 since these parameters are controllable in the experiment for a given fibre sample by tuning the pump frequency and power. The input power Pin was scanned in the interval from 0.4 W to 0.8 W in steps of 0.025 W and the phase shift Δφ0 from 0 to 2 π in steps of 0.05 π. For each set of parameters the coupled mode equations were integrated and an analysis (see Methods section for more details) was performed to determine whether the powers and the parameter ϑ+(L,t) reach a steady state.

The result of this parameter scan is shown in Fig. 6. The black area corresponds to the case where the phase parameter ϑ+(L,t) and the powers reach a steady state corresponding to phase-locking and result in a stable interference signal at the output of the fibre. These results qualitatively correspond to the result shown in Fig. 5(b). For the white area in Fig. 6, the parameter ϑ+(L,t) does not reach a stable state and no stable interference signals are obtained (similar to the result shown in Fig. 5(a)).

Figure 6
figure 6

Domains of phase-locking for different input powers Pin and phase shifts Δφ0.

Black: Phase-locking (∂ϑ+(L,t)/∂t = 0). White: Drifting phase parameter (∂ϑ+(L,t)/∂t ≠ 0).

Full size image

The same parameter scan was also performed for using the coupled mode equations without the FWM terms. We observed that without FWM there is no regime where the parameter ϑ+(L,t) reaches a steady state.

Discussion

In this paper, we demonstrated phase-locking of BFCs generated by quasi-CW pumping of a short, low finesse Fabry-Perot resonator (Fig. 2(b)). By repeating the experiment with the same initial conditions we have shown that a mechanism exists that phase-locks the BFC with a particular phase-relationship leading to the generation of stable trains of pulses (Fig. 4). Numerical simulations that included FWM showed a strong qualitative agreement with the experimental results and revealed that FWM is essential for phase-locking and the generation of stable pulse trains. Discrepancies between experimental and simulation results are attributed to uncertainties of experimental parameters and to the neglect of power transfer to higher order (>2) Stokes waves and anti-Stokes waves in the numerical model.

In the experiment, quasi-CW light has been used in order to minimize thermal effects and to achieve high peak powers that are necessary in the current configuration. In the future, we will investigate performing the experiment with CW light and explore different configurations that will reduce the necessary peak power. CW generation of the BFC will also allow us to further assess the possibilities of applications and to perform a deeper analysis of the comb stability15,35.

In developing the model we assumed negligible dispersion. This assumption is justified since the cavity length L ≈ 38 cm is 4 orders of magnitude shorter than the coherence length of the degenerate FWM process33 that is calculated using the material dispersion42D of As2Se3.

The frequency detunings of the pump and Stokes waves with respect to the cavity resonances (described by the parameter Δφ0) are sensitive to temperature drift of the resonator leading to a varying output of the resonator on a time scale of a few seconds. Besides active stabilization47, reducing the cavity length and therefore increasing the FSR of the cavity could be used to improve stability. Recently, SBS has been demonstrated on photonic chips made of chalcogenide glass exploiting large SBS gain as well as strong mode confinement48,49,50. Quasi-CW generation of several orders of Stokes waves has been demonstrated on-chip in a low finesse Fabry-Perot cavity of only a few cm length18. On-chip generation of phase-locked pulse trains via SBS and FWM promises a much higher degree of stability as well as more compact devices and will also be subject of future investigations.

Methods

A schematic of the experimental setup used is shown in Fig. 7. In order to perform the experiment in a quasi-CW regime, the output of a continuous wave laser operating at 1550 nm with a linewidth of 500 kHz was carved into 500 ns square pulses at 20 kHz repetition rate using an optical intensity modulator with extinction ratio of ~27 dB. This increased the linewidth of the pump to about 1.8 MHz. The modulator was followed by an erbium doped fibre amplifier (EDFA) to increase the peak intensity of the pulses. Modulating the CW light allowed us to perform the experiment with high peak powers (~1 W) while keeping the coupled average power low (~10 mW). A polarisation controller was placed after the modulator to align the polarisation of the pump light with a polarisation mode of the chalcogenide fibre resonator. This was achieved by setting the pump power just above the threshold for the generation of the first-order Stokes wave and then adjusting the polarisation such that the power of the first-order Stokes wave is maximised. We used a 38.29 cm long As2Se3 step-index fibre (CorActive Inc.) with core and cladding diameters of ~5.25 μm and ~170 μm, respectively. The numerical aperture of the fibre was NA = 0.17. Light was coupled into and out of the As2Se3 fibre by butt-coupling high numerical aperture silica fibres. An optical spectrum analyser (resolution ~ 10 pm) allowed spectral characterization of the output and a photodiode (bandwidth ~ 50 GHz) connected to a real-time oscilloscope (80 GSa/s, bandwidth 33 GHz) enabled real-time analysis of the transmitted signal. The real-time oscilloscope also allowed the recording of 110 consecutive pulse traces. In Fig. 4(a) and 4(b) every tenth trace of such a measurement is plotted.

Figure 7
figure 7

Schematic of the experimental Setup.

MOD: Optical intensity modulator. EDFA: Erbium-doped fibre amplifier. PC: Polarization controller. PD: Photodiode. RT-Scope: Real-time oscilloscope. OSA: Optical spectrum analyser.

Full size image

Details about the coupled mode equations used for the numerical study can be found in the Supplementary Information. For the numerical integration of the time dependent couple mode equations we transformed the variables into frames moving with forward and backward propagating optical fields, respectively28,51 and used the integration method described by de Sterke et al.51. Steady states of the phase parameter ϑ+(L,t) and the powers were determined by integrating the coupled mode equations for a time interval of 6 μs and calculating the standard deviations σ(ϑ+) and of ϑ+(L,t) and , respectively, in the time interval [5 μs,6 μs]. ϑ+(L,t) was considered to have reached a steady state if σ(ϑ+) < 10−3 × 4π. The power were considered to have reached a steady state if , where are the mean values of in the interval [5 μs,6 μs].