Abstract
The distribution of mutational fitness effects (DMFE) is crucial to the evolutionary fate of quasispecies. In this article we analyze the effect of the DMFE on the dynamics of a large quasispecies by means of a phenotypic version of the classic Eigen's model that incorporates beneficial, neutral, deleterious and lethal mutations. By parameterizing the model with available experimental data on the DMFE of Vesicular stomatitis virus (VSV) and Tobacco etch virus (TEV), we found that increasing mutation does not totally push the entire viral quasispecies towards deleterious or lethal regions of the phenotypic sequence space. The probability of finding regions in the parameter space of the general model that results in a quasispecies only composed by lethal phenotypes is extremely small at equilibrium and in transient times. The implications of our findings can be extended to other scenarios, such as lethal mutagenesis or genomically unstable cancer, where increased mutagenesis has been suggested as a potential therapy.
Similar content being viewed by others
Introduction
Eigen's model of molecular quasispecies 1,2,3, initially conceived to explore prebiotic evolution, has played a key role in understanding the population dynamics and evolution of RNA viruses4,5,6,7. Due to the complexity of these pathogens, some theoretical assumptions and predictions fail to catch important properties of viral dynamics and adaptation8. For instance, assumptions made considering simple fitness landscapes generally predict the presence of transitions towards error threshold or extinction regimes as mutation rates increase9,10,11. However, biological evolution proceeds on more complex, rugged fitness landscapes3,12,13 and, outstandingly, not all mutations exert the same effect on viral fitness14,15.
Efforts have been made to expand the basic quasispecies theory by relaxing its original assumptions and incorporating more virus-realistic features: fitness landscapes with multiple peaks16, neutrality and robustness17,18, spatial effects10,19,20,21, complementation during coinfection22,23 and different modes of replication and epistasis21,24, among others. Despite all these modeling approaches, there is still a major factor that remains poorly explored by the standard quasispecies model: realistic distributions of mutational fitness effects (DMFE). DMFE may exert a strong impact in the evolutionary dynamics of a large quasispecies population. Therefore, our aim in this study is to provide a broader framework by incorporating experimentally available DMFE within quasispecies evolutionary dynamics.
The fitness effects of mutations are central to evolution25,26,27. Several experiments quantifying the fraction of spontaneous mutations as either selectively beneficial, neutral, deleterious or lethal have been performed in, e.g., Arabidopsis thaliana28, Drosophila melanogaster29,30, bacteria31 and viruses14,15,32,33. The efforts made by virologists in describing DMFE have not been mirrored by theoretical research in quasispecies populations. As yet, few models have explicitly considered the DMFE in asexual replicators34,35 and none of them have parameterized the standard quasispecies model with experimentally available data on DMFE. Furthermore, the impact of the DMFE on the error threshold and how they may promote or constrain the generation of deleterious or lethal phenotypes in a large quasispecies population (e.g., in persistently infected hosts) remains unknown.
The error threshold is a theoretical average mutation rate that sets a maximum limit for maintenance of genetic information encoded by a replicating system36. Usually, the error threshold takes place when the pool of mutants displaces the wild-type sequence due to increased mutation. It is important to mention that the error threshold implicitly depends on the fitness landscape37; e.g., for the single-peak fitness landscape, the error threshold occurs when the homogeneous cloud of mutants with lower fitness outcompetes the wild-type sequence1,2,10,11. In order to introduce a more realistic fitness landscape into the quasispecies model, as well as to consider realistic DMFE that determine how mutation moves the quasispecies within this landscape, we analyze a phenotypic quasispecies mathematical model incorporating variable mutational fitness effects (see Figure 1).
Population structure of the phenotypic quasispecies.
Sequences can carry beneficial (B), neutral (N), deleterious (D) and lethal (L) mutations (bit 0 means non-mutated and bit 1 means mutated). (a) Phenotypic sequence space where ball size indicates strings' replicative fitness. The inner green cube contains the lethal mutants. The fitness of some strings is shown on a fitness landscape with dashed arrows. The landscape has three different peaks available through mutation: wild-type (W), beneficial (B) and deleterious (D) peaks, while the ground (light blue) indicates the lethal (L) phenotype with zero replication. Strings x1010 and x1110 will occupy peaks W, B, or D, depending on the values of the selection coefficients sB and sD. (b) Example of replication with mutation for string x1110, with replication rate A1110 = 1 + sB − sD. Gray arrows denote mutation transitions. (c) Sequences of the quasispecies (1st column), their phenotypes (2nd column) and their fitnesses determined by the replication rates, Ai (3rd column).
Here, we will first investigate the impact of increasing mutation rate on the phenotypic distributions and on the viability of the quasispecies integrating available experimental data on the DMFE for two RNA viruses: the animal pathogen Vesicular stomatitis virus14 and the plant pathogen Tobacco etch virus15. Second, we will investigate the dynamics for the general model with and without phenotypic reversion, since we are especially interested on a detailed analysis of the dependence of the results with respect to the model parameters. Finally, we perform an extensive search in the parameter space to evaluate the likeliness of finding parameter combinations that impair the success of viral phenotypes, driving the quasispecies towards lethal and deleterious vertices of the phenotypic sequence space.
Results
We refer the reader to the Model and Methods section and to Section 1 in the Supplementary Information for a detailed description of the mathematical model and, in particular, for the notation and meaning of variables and parameters that we use in what follows.
Dynamics with realistic DMFE
First, we present results on the model Eqs. (1) incorporating DMFE data for VSV and TEV and considering that phenotypic reversions (via backward or compensatory mutations) are not possible. Previous theoretical work has assumed that the likelihood of backward mutations was extremely small due to the length of RNA viral genomes10,19,22, while other models have incorporated backward mutations in the dynamics of quasispecies16,38. The case with no backward mutations (no phenotypic reversion) can be studied in our model by setting δ = 0 (being δ the probability of phenotypic reversion in the quasispecies, see Model and Methods section). Under our model assumptions, together with δ = 0 and considering no production of beneficial mutations i.e., λB ≠ 0 (see Model section), Eqs. (1) have two equilibrium points (given as Q3 and Q4 in Section S4 of Supplementary Information). When no phenotypic reversion is allowed (i.e., δ = 0), the relevant fixed point for VSV data is given by Q3 (see SI Section S4). This fixed point, which is an attractor under the parameter values for VSV, can be represented for the sake of clarity as: ( ,
,  ,
,  ,
,  ,
,  ), where
), where  and
and

with Ψ = sD(1 − μ)2 + [(1 + sB)λDμ + sDλLμ] (1 − μ) + (1 − sD + sB)λDλLμ2. Here sD and sB are the selection coefficients tied to deleterious and beneficial mutations, μ is mutation rate and λD and λL are the frequencies of production of deleterious and lethal phenotypes during the process of replication and mutation (see Model and Methods section for further details on the parameters of the model). The previous equilibrium point involves the persistence of four different sequences:  ,
,  and the lethals
and the lethals  and
and  . That is, when δ = 0 and λB > 0 (i.e., no phenotypic reversion for VSV), 12 of the 16 different sequences of the quasispecies will asymptotically achieve extinction and four types of sequences will only compose the quasispecies: a neutral mutant with the beneficial phenotype (
. That is, when δ = 0 and λB > 0 (i.e., no phenotypic reversion for VSV), 12 of the 16 different sequences of the quasispecies will asymptotically achieve extinction and four types of sequences will only compose the quasispecies: a neutral mutant with the beneficial phenotype ( ) and the sequence with neutral, beneficial and deleterious mutations (
) and the sequence with neutral, beneficial and deleterious mutations ( ). The other two sequences have the lethal phenotype (i.e.,
). The other two sequences have the lethal phenotype (i.e.,  and
and  ). These results perfectly match with the time series shown in Figure S1. Moreover, projections of the dynamics in the simplex suggest that such a fixed point is globally stable (Figure S2), which has been confirmed analytically in SI Section S4.
). These results perfectly match with the time series shown in Figure S1. Moreover, projections of the dynamics in the simplex suggest that such a fixed point is globally stable (Figure S2), which has been confirmed analytically in SI Section S4.
The effect of increasing mutation involves the extinction of the non-mutated genomes at equilibrium (Figure 2). Such extinction is mainly due to outcompetition by the beneficial phenotype x1100, which is present in the quasispecies in a wide range of mutation rates, independently of the values of the selection coefficients sB and sD [Figure 2(a) and (c)]. Two of the sequences found at equilibrium are lethal mutants, but the quasispecies for VSV is mainly dominated by the neutral mutants carrying a beneficial mutation and by sequence x1110 in a wide range of mutation rates. The case with sB = 0.25 and sD = 0.9 actually makes the sequence x1100 much more dominant in a large range of mutational values [Figure 2(c)]. For more details on the dynamics using VSV DMFE data see SI Section S4.
Impact of increasing mutation rate in the population equilibria without phenotypic reversion.
Here we use δ = 0 (i.e., no phenotypic reversion) and DMFE data for Vesicular stomatitis virus (VSV)14 and Tobacco etch virus (TEV)15. In (a) and (c), we display the equilibrium populations for VSV: x1100 (black); x1110 (red); x1101 (green); and x1111 (blue). In (b) we show equilibrium populations for TEV: x0100 (violet); x0110 (cyan); x0101 (maroon); and x0111 (dark green). For both VSV and TEV, all other variables have zero population numbers at equilibrium. We used: (a) sB = 1 > sD = 0.25; (b) sB = sD = 0.5; and (c) sB = 0.25 < sD = 0.9.
A qualitatively different dynamics is found for the DMFE data for TEV without phenotypic reversions. Here λB = 0 gives rise to a different fixed point given by Q1 (see SI Section S4). For this case, the equilibrium also consists of four sequences:  ,
,  and the lethals
and the lethals  and
and  . Similarly to VSV, the dominant sequences at increasing mutation are the sequences with only neutral and with both neutral and deleterious mutations. Lethal sequences become abundant only when mutation rate is extremely high [Figure 2(b)]. Some examples of the time dynamics and phase portraits for TEV DMFE data can be found in Figs. S3 and S4.
. Similarly to VSV, the dominant sequences at increasing mutation are the sequences with only neutral and with both neutral and deleterious mutations. Lethal sequences become abundant only when mutation rate is extremely high [Figure 2(b)]. Some examples of the time dynamics and phase portraits for TEV DMFE data can be found in Figs. S3 and S4.
Interestingly, our results reveal that the fittest phenotype does not go extinct as we might expect. The usual error threshold sets in when μ = 1 − [wunfit/wfit], where wunfit and wfit are, respectively, the lowest and the highest fitnesses of the sequences39. For example, according to this prediction, we would expect the extinction of the sequence 1100 for VSV when μ > μc = 1 − [(1 − 0.25)/1] = 0.25. However, the panels (a) and (c) of Figure 2 show persistence of 1100 at this mutation rate and higher. Hence, the simple expectation previously defined fails. The reason for this phenomenon may be due to the fact that the unfit subpopulation (1110) is constantly loosing members to the lethal class (1111) and then wunfit should be weighted in the previous calculation to include these lethal members, which might prevent the error catastrophe.
When phenotypic reversions are allowed, i.e., δ ≠ 0, the non-mutated strings (i.e., wild-type string x0000) also decrease their population density dramatically as mutation is slightly increased. This finding is common for both VSV and TEV DMFE data. However, such a population is maintained by keeping its equilibrium in small populations for VSV DMFE data, i.e.,  , for the whole range of mutation rates (see Figure 3 and panels (d–f) in Figure S1). This effect also takes place for different values of the selection coefficients but is less dramatic for TEV data, where
, for the whole range of mutation rates (see Figure 3 and panels (d–f) in Figure S1). This effect also takes place for different values of the selection coefficients but is less dramatic for TEV data, where  (Figure 3 and panels (d–f) in Figure S3). A plausible explanation for this effect is that as TEV does not produce beneficial mutants, competition is weaker and thus the wild-type phenotype can persist even for high mutation rates. For VSV, however, the equilibrium populations of the strings with the beneficial phenotype (i.e., sequences x1000,1100) undergo a dramatic increase for very low mutation rates in all the scenarios analyzed in Figure 3. Typically, such sequences decrease their population numbers at increasing mutation rates (see also Figure S5). Hence, for both VSV and TEV examples, when phenotypic reversions are allowed, no error thresholds exist at which the wild-type sequence (and its neutral mutants) disappear from the population. For the particular case considering phenotypic reversion, explicit analytical approximations can be derived assuming that the probability of phenotypic reversion is small (i.e.,
(Figure 3 and panels (d–f) in Figure S3). A plausible explanation for this effect is that as TEV does not produce beneficial mutants, competition is weaker and thus the wild-type phenotype can persist even for high mutation rates. For VSV, however, the equilibrium populations of the strings with the beneficial phenotype (i.e., sequences x1000,1100) undergo a dramatic increase for very low mutation rates in all the scenarios analyzed in Figure 3. Typically, such sequences decrease their population numbers at increasing mutation rates (see also Figure S5). Hence, for both VSV and TEV examples, when phenotypic reversions are allowed, no error thresholds exist at which the wild-type sequence (and its neutral mutants) disappear from the population. For the particular case considering phenotypic reversion, explicit analytical approximations can be derived assuming that the probability of phenotypic reversion is small (i.e.,  ). We refer the reader to Supplementary Information Sections S5 and S6 for detailed calculations.
). We refer the reader to Supplementary Information Sections S5 and S6 for detailed calculations.
Population equilibria for sequences and phenotypes at increasing mutation considering phenotypic reversion.
We here consider phenotypic reversion (δ = 10−3) and DMFE data for VSV and TEV (in linear-log scale) with: (a) sB = sD = 0.5 and (b) sB = 0.25 < sD = 0.9. In the first row we display sequences: x0000 (black line) and the pool of mutants in red lines (except for strings x0100 (dotted red line), x1000 (dashed red line); and x1100 (blue line)). For clarity, phenotypes in the second row are grouped as follows: sequences x0000 plus x0100 (wild-type, W, in black); x1000 plus x1100 (beneficial, B, in green); x0010 plus x0110 (deleterious, D, in blue); and lethal (L, in red) with the sum of all sequences with bit 1 in the last position; and x1010 plus x1110 (sequences with beneficial and deleterious mutations, in violet). Sequences x1010 and x1110 can be included in phenotypic classes W, B, or D, depending on the values of the selection coefficients [i.e., sD = sB (W), sD < sB (B) and sD > sB (D)].
We notice that for VSV there is an available beneficial mutation and since reversions are rare, both mutational and selective pressures favor it and all sequences at equilibrium have 1 in the first position. Similarly, the neutral bit is favored by mutation and neutral selection; thus every sequence has it as well. For TEV the situation is similar, but since there are no beneficial mutations, the first bit is always 0. In either case, this is essentially a 2-locus problem.
In the previous analyses we have considered experimental DMFE to characterize the dynamics of Eq. (1). Since the proportion of mutations that are effectively neutral, beneficial and deleterious may vary for other species, we provide analytical and numerical results of the model as a function of all parameters, including arbitrary values of the DMFE, given by λk. These analyses can be found in Supplementary Information Sections S4, S5, S6 and S7 (see also next sections).
Exploration of the parameter space
The previous results without phenotypic reversion reveal the existence of error thresholds shifting the quasispecies towards beneficial, neutral, deleterious and lethal regions of the phenotypic sequence space in an asymmetric manner. The error threshold has been discussed as a phenomenon causing the loss of viral genetic information due to increased mutation19. Actually, the error threshold is an evolutionary transition in sequence space that can delay or even prevent extinction by moving the population towards genotypes that are robust to extinction40, as our results indicate, i.e., we characterized persistence of beneficial and neutral phenotypes at equilibrium for a wide range of mutation rates (see Figures 2 and 3).
In this context, our theoretical approach allows us to address the following question: what is the likelihood of finding scenarios in which genomes fail to replicate and thus the viral population is only composed of deleterious and/or lethal phenotypes? To explore this question, let us define three different scenarios given by a quasispecies with different equilibrium population values, N*, as follows:
-
Scenario (A): N* lethal mutants,
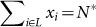 , i.e., sum of the populations of lethal sequences.
, i.e., sum of the populations of lethal sequences. -
Scenario (B): N* lethal plus deleterious mutants,
 , i.e., sum of scenarios (A) and (C).
, i.e., sum of scenarios (A) and (C). -
Scenario (C): N* deleterious mutants,
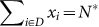 , i.e., sum of the sequences with the deleterious phenotypes, and, if sD > sB, adding also the sequences with both deleterious and beneficial mutations with fitness A = 1 + sB − sD).
, i.e., sum of the sequences with the deleterious phenotypes, and, if sD > sB, adding also the sequences with both deleterious and beneficial mutations with fitness A = 1 + sB − sD).
All our previous analyses using VSV and TEV data suggest that the possibility to push the entire quasispecies towards lethality by increasing mutation (scenario (A) with N* = 1) may be very unlikely due to variable DMFE. To test the generality of this result, we perform an extensive search in the parameter space of Eqs. (1), which allows us to identify those parameter combinations fulfilling scenarios (A), (B) and (C) for different values of N*. To do so, we use a MonteCarlo (MC) algorithm to randomly sample the parameter space of Eqs. (1) (see Model and Methods section). The results obtained without phenotypic reversion are shown in Table I and in Figure 4. We found that the mean percentage of parameter combinations, 〈p*〉 · 100, that push the quasispecies towards lethal vertices of the phenotypic space is extremely small (see parameter spaces (λL, μ) and (μ, λB) for scenario (A) in Figure 4). For instance, such a percentage is about 1.88% using N* ≥ 0.9. As expected, the parameter values responsible of increasing populations of lethal sequences are mainly those combinations involving extremely high mutation rates, although such mutation can diminish at increasing values of λL. However, as we display in the histogram of Figure 4, the likelihood to push the whole quasispecies towards lethality is very small. Specifically, the histogram displays the mean percentage of parameter combinations for each value of N* and scenario, averaged over 100 independent replicas, where each replica corresponds to M = 106 iterations of the MC algorithm.
Exploration of the parameter space of Eqs. (1) without phenotypic reversion (i.e., δ = 0).
We plot two-dimensional parameter space projections using M = 106 iterations of the MonteCarlo (MC) algorithm displaying parameter values pushing the quasispecies towards scenarios (A), (B) and (C) for different population equilibria, N*: N* ≥ 0.6 (cyan), N* ≥ 0.7 (violet), N* ≥ 0.8 (yellow) and N* ≥ 0.9 (maroon). Note that N* ≥ x* includes all values of y* > x* (e.g., N* ≥ 0.6 includes all other N* values analyzed). The histogram displays the mean percentage of parameter combinations, 〈p*〉 · 100, with 〈p*〉 = 〈c(N*)/M〉, fulfilling scenarios (A), (B) and (C) for the investigated values of N* (using the same colors for each value of N* previously described). Each bar was computed over 100 independent replicas of the MC algorithm (each replica run for M = 106 iterations), standard deviation (SD) not shown (see Table I below).
Our results also reveal that when beneficial mutations are less common, mutation rate does not need to be so high to produce some fraction of the population composed by lethal sequences, although it is also very unlikely to have a quasispecies fully composed by lethal sequences (it simply will not replicate). We also found that the selection coefficients have a little effect in scenario (A), since no clear pattern is shown for the different values of N* in the parameter space projection given by (sD, sB) that is displayed in Figure 4. Concerning to scenario (B), where we put together lethal and deleterious genomes, the percentages of parameter combinations pushing the whole quasispecies to this scenario is larger than for scenario (A). For instance, the probability of finding parameter combinations with a quasispecies composed by N* ≥ 0.9 lethal plus deleterious sequences is about 6.8%, which is still a low value. Here, as we identified in the previous analyses, selection coefficients do not play an important role in this scenario. Finally, the percentage of parameter combinations pushing the quasispecies to deleterious nodes in the phenotypic sequence space is also extremely low. We may notice also that having a population dominated by deleterious mutants does not imply that viral sequences will not be able to replicate, since some of the deleterious sequences will be able to replicate whenever sD is small. For instance, a sequence with the deleterious phenotype will be able to replicate at a rate A = 0.8 when sD = 0.2.
The exploration of the parameter space considering phenotypic reversion reveals that the percentage of parameter combinations driving to lethality decreases even more (see Supplementary Information Section S7 for further details). All together, the previous results suggest that the quasispecies is very unlikely to be driven toward full lethality by manipulating the parameters of the model, including mutation rates (see Figures 2,3,4, Supplementary Information Section S7 and Figures S5–S7). We performed an ANOVA test with the data displayed in Table I, taking “scenario” and “phenotypic reversion” as fixed factors and “N*” as a variable and covariable. Factor “scenario” had a significant effect (P < 0.0001) with the following rank: (B) > (A) > (C). In other words, 〈p*〉 was larger in scenario (B) than in (C), with (A) occupying an intermediate position. “Phenotypic reversion” had a significant effect (P = 0.0165), with lower values of 〈p*〉 when phenotypic reversion was allowed and higher when it was not allowed, meaning that phenotypic reversion actually makes lethality much more difficult. The covariable “N*” also had a significant effect (P < 0.0001), with the largest values of 〈p*〉 when N* is lower, indicating that the probability of having the majority of sequences in lethal vertices was small in this case. Of all interactions between the factors and the covariable, the only significant one was “scenario” × “N*” (P < 0.0001), meaning that differences between scenarios are bigger for small N* than for large values of N*.
The previous estimations of the percentages of parameter combinations pushing the quasispecies towards population values N* for scenarios (A), (B) and (C) were computed at equilibrium. But, how do these probabilities behave in transient time? To answer this question, we performed similar analyses for N(t) instead of N*. That is, we used the MC algorithm to quantify the fraction of parameter combinations involving different population values for scenarios (A), (B) and (C) at a given time, t (we used t = 102, t = 103 and t = 104). This strategy allows us to explore the likelihood of these scenarios taking place also during transients. The results, displayed in Supplementary Information Table S1, revealed that such percentages are indeed smaller during transients, especially when δ = 0. For instance, the probability of finding parameter combinations that push the quasispecies towards scenario (A) considering N(t = 100) ≥ 0.9, is 〈p(t)〉 ≈ 0.0066, which is approximately 3-fold lower than the same probability computed at equilibrium. As expected, such probabilities get close to the probabilities computed at equilibrium for larger values of time. Similar results were found for scenarios (B) and (C) (see Supplementary Information Table S1).
The ANOVA of data from Table S1, found a net effect of time (P < 0.0001): time has a different behavior for each scenario (P < 0.0001). For scenario (A), 〈p(t)〉 for the first evaluated time (i.e., t = 102) is significantly lower than for the other two scenarios, which remain the same. In scenario (B), this difference was even smaller and in (C) this difference was not found. These data indicate that for t = 102 the convergence to equilibrium in scenario (A) has not been reached and thus the system is in the transient state, but for scenarios (B) and (C) the system is almost at equilibrium. We notice that the values of 〈p(t)〉 displayed in Table S1, are typically lower in transient time, meaning that the probability of pushing the quasispecies toward lethal vertices of the phenotypic sequence space is smaller during the transient time, although such values closer to equilibrium also remain very small, specially for large values of N(t).
Transient regimes as a function of δ and other parameters
We are particularly interested in the effect of the probability of phenotypic reversion, δ, on transient times (see Model and Methods section). Our results indicate that the smaller δ the longer is the time needed to approach the fixed point at the given distance η. This time depends on two things: the component of the initial data in the eigenvector of the matrix A in the direction of x* and on the eigenvalue of DF(x*) closest to zero. As discussed in Supplementary Information Section S5, the smaller is δ the closest is the eigenvalue to zero and, hence, the required time is larger.
It is worth to remark that the fraction of M* for which the approximation to distance η to x* is not produced at the final integration time tmax is extremely small: around 0.00002 for δ = 10−3 and increases to 0.00022 for δ = 0.
Figure S8(left) shows the results using M* = 108 and η = 10−3 for the values δ = 10−3, 10−4, 10−5, 10−6, 10−7 and δ = 0, from left to right. On the horizontal axis τ is represented in log10 scale. The value of tmax is set equal to 108.
What happens if η is reduced? Of course, the transient time, until the distance to x* is less than η, will increase. To illustrate this fact we reproduce in Figure S8(right) the same curves in the left plot for δ = 10−3, 10−5 and 0 for η = 10−3 (in red) and we show the corresponding curves for η = 10−6 in blue. We see that in the first two cases the curves shift a little to the right, while in the δ = 0 case they shift by a large amount. The computations for η = 10−6 use again tmax = 108 but M* is reduced to 106.
Now, while for δ = 10−3 still only a small fraction, around 0.00005, of cases do not approach x* at the distance η at the maximum time, this fraction increases dramatically to 0.076 for δ = 0.
According to the theory developed in Supplementary Information Sections S4 and S5, if δ > 0 is small the final approach to x* is of the form exp(−γδ1/2) where γ is the coefficient of δ1/2 in Eq. (33) of the Supplementary Information. On the other hand, for δ = 0 the approach to x* is like a constant divided by t.
From the data which allow to produce Figure S8 (right), one can compute, by Lagrange interpolation, the values of τ for different values of φ(τ). We have selected values of φ(τ) of the form 0.1 k, k = 1, …, 9. Let τ1 be the value of τ when η = η1 = 10−3 and τ2 the one for η = η2 = 10−6. For δ > 0 the decrease of η should satisfy, approximately,

The value of γ depends on the average value of the random parameters and also on the value of φ(τ).
Hence, the decrease of δ1/2 by a factor of 10 should be compensated by an increase of τ2 − τ1 also by a factor of 10. This is shown in Figure S9. The red and blue curves show log10(τ2 − τ1) for different values of φ(τ). The differences are very close to 1, as expected. On the opposite case, δ = 0, the green curve shows log10(τ2/τ1). It is almost exactly equal to 3, in perfect agreement with the fact that log10(η2/η1) = −3. Summarizing, this analysis and numerical checks allow obtaining good indications on the rate of approach to the fixed point.
Discussion
In this article we have extended Eigen's quasispecies model using a phenotypic description of the quasispecies that considers variable distributions of mutational fitness effects (DMFE), which are known to be crucial to RNA virus evolution25,26. Although the DMFE has been experimentally quantified for several viruses14,15,32,33, previous theoretical models34,35 have not deeply analyzed the effect of the DMFE in persistently infected hosts. Moreover, none of them included these experimental data in the standard quasispecies model. Here we intend to cover this gap, paying special attention to the interplay between the DMFE and mutation in possible deleterious or lethal scenarios in large viral quasispecies populations. The interest in characterizing the effects of artificially-increased mutation (mutagenesis) in viral replicators comes from the fundamental prediction of the classic quasispecies theory1,2: error-prone replicators have a limited tolerance to mutations, beyond which an error catastrophes takes place and the genetic information is lost. Several models have shown that when mutation rate is increased, the population moves towards lower fitness classes and the average fitness of the quasispecies or the average growth rate per generation diminishes39,40,42,43. In such a case, for discrete systems, when the average growth rate becomes smaller than one, the population enters into an extinction regime that causes the disappearance of the quasispecies.
Previous works on the induction of mutagenesis in poliovirus and VSV revealed a 100-fold decrease in viral titers44,45. Further experimental evidence confirming the effect of mutagens in decreasing infectivity and replication was later described for HIV-1 in tissue cultures46. Similar results were also found for Lymphocytic choriomeningitis virus, hantaviruses and Hepatitis C virus, among others (see review47). Despite these previous investigations, the feasibility of entirely pushing a quasispecies towards lethality by manipulating external parameters such as mutation rates still remains a matter of debate, especially in persistently infected patients, i.e., in quasispecies with large population numbers. Our model, aimed to answer this question, predicted that an external forcing towards lethality (e.g., increased mutagenesis) would be unlikely to be found in large quasispecies populations. The generation of different mutational types seems enough to ensure the persistence of viable viral genomes, even if highly deleterious or lethal mutations are constantly produced.
Our theoretical approach does not include other possible sources that could enhance viral extinction or involve significant viral fitness decrease. For instance, we consider soft selection, i.e., no degradation of sequences, because we are mainly interested in the net effects of mutation rate, DMFE and phenotypic reversions in the viability and lethality of the viral phenotypes. Also, we are not considering discreteness (individual based model) or finite populations with stochasticity41 (e.g., lethal defection48), or bottlenecks during transmission events that turn on Muller's ratchet (shown to operate in phages φ649 and MS250 VSV51, TEV52, Foot-and-mouth disease virus53 and human immunodeficiency virus type 154). As mentioned, the standard quasispecies model (and thus our model as well) does not consider sources of stochasticity, suggested to be important in realistic experimental systems as well as during initial infections, when the number of viral particles can be extremely low. However, as we previously discussed, we considered a deterministic quasispecies model as a proxy to characterize the effect of the DMFE during a persistent infection, for which intrinsic or demographic noise of viral populations might be negligible. Further research should include these factors in quasispecies dynamics together with DMFE.
Our model predicts that increasing mutation rates may not be enough to drive viral quasispecies towards highly deleterious or lethal phenotypes in large populations, as may be those typical of persistent infections. It would be interesting to perform experiments like those described in Refs. 14 and 15, in which the properties of the DMFE were evaluated, but at artificially increased mutation rate. Such experiments would facilitate the comprehension of the role played by the DMFE at increasing mutation in possible lethal scenarios for viral quasispecies in vivo, also allowing to test our prediction. Moreover, these experiments would also give clues about the interplay between mutation and the DMFE, an important issue, that, to the extent of our knowledge, remains unknown.
We notice that our results may also be relevant in the context of lethal mutagenesis. Lethal mutagenesis refers to a viral population's extinction through an excess of mutations, often promoted by mutagenic nucleotide analogs administered during viral replication8,36,41. Lethal mutagenesis is a demographic phenomenon that operates in finite populations, not considered in our model. Nonetheless, our model indicates that the chances to enter into a regime of declining viral populations may be very unlikely, since the variability in the DMFE will constantly keep available phenotypes able to successfully replicate in the population.
As a final point, the theoretical framework and the results presented here, developed for viral quasispecies, may also have implications in carcinogenesis. In cancer, the maximum amount of genetic instability that can be tolerated by tumor cells, suggested to also behave as quasispecies, has been proposed55,56. Genomic instability57,58 is a hallmark of most malignant tumors, which could be ablated by increased mutagenesis59,60,61. Our model suggests that the success of such strategies should be weighted by the corresponding distribution of mutational fitness effects, which can be defined by taking into account the distinct roles played by genes affecting proliferation, DNA repair or apoptosis, along with house-keeping62. The potential success of suppression of tumor growth through mutation-induced lethality as well as the resistance of some clones to drugs should be considered as two faces of the unstable tumor dynamics, which may require considering the repertoire of mutational fitness effects.
Methods
Model
To analyze the impact of the DMFE on viral quasispecies we build a phenotypic mathematical model using Eigen's formulation1. The model describes the time dynamics of i classes of binary sequences with population numbers xi able to carry different mutational types that can replicate and mutate according to the differential equations:

with  , being
, being  the configuration or sequence space (i.e., boolean ν-dimensional hypercube), with
the configuration or sequence space (i.e., boolean ν-dimensional hypercube), with  and ν = 4, resulting in a quasispecies composed by n = 16 different sequences. Each sequence has 4 bits, each of them corresponding to each particular type of mutation: beneficial (B, 1st bit), neutral (N, 2nd bit), deleterious (D, 3rd bit) and lethal (L, 4th bit), as we display in Figure 1. Our model becomes a generalization of the classic Eigen's quasispecies model2, which incorporates new parameters to introduce variance in fitness effects due to mutation and, eventually, phenotypic reversion. We refer the reader to Ref. 38 for a stochastic model similar to Eqs. (1).
and ν = 4, resulting in a quasispecies composed by n = 16 different sequences. Each sequence has 4 bits, each of them corresponding to each particular type of mutation: beneficial (B, 1st bit), neutral (N, 2nd bit), deleterious (D, 3rd bit) and lethal (L, 4th bit), as we display in Figure 1. Our model becomes a generalization of the classic Eigen's quasispecies model2, which incorporates new parameters to introduce variance in fitness effects due to mutation and, eventually, phenotypic reversion. We refer the reader to Ref. 38 for a stochastic model similar to Eqs. (1).
The first term of Eqs. (1) is the error-free replication of string i with replication rate Ai and mutation rate μ. The second term corresponds to the influx of mutant strings j from orthant neighbors (denoted as <j>i) of  producing string i by mutation. Parameters
producing string i by mutation. Parameters  , with
, with  , denote the fraction of mutations with a fitness effect k ∈ {B, N, D, L} from sequence j to sequence i during error-prone replication. These parameters are used to incorporate the DMFE in our model (see Section Experimental data below). Parameter β[j→i] is the probability of occurrence of transitions 0 → 1 and 1 → 0 (i.e., phenotypic reversion) from sequence j to sequence i during replication, with:
, denote the fraction of mutations with a fitness effect k ∈ {B, N, D, L} from sequence j to sequence i during error-prone replication. These parameters are used to incorporate the DMFE in our model (see Section Experimental data below). Parameter β[j→i] is the probability of occurrence of transitions 0 → 1 and 1 → 0 (i.e., phenotypic reversion) from sequence j to sequence i during replication, with:

We notice that our approach allows us to model the process of mutation considering no backward mutations (i.e., no phenotypic reversion), setting δ = 0; as well as to model phenotypic reversions due to backward or compensatory mutations (with δ > 0). The total population is held constant (i.e.,  ) by a compensating dilution flux with rate coefficient Φ. The outflow term, Φ, is obtained under the constant population condition, i. e.,
) by a compensating dilution flux with rate coefficient Φ. The outflow term, Φ, is obtained under the constant population condition, i. e.,  , giving:
, giving:

The state space of system (1) is a high-dimensional simplex (i.e., 2ν − 1 simplex) represented by the nonnegative vectors  . As initial conditions we will use (if not otherwise specified) x0000(0) = 1, setting all other variables to zero.
. As initial conditions we will use (if not otherwise specified) x0000(0) = 1, setting all other variables to zero.
All 24 different strings of the quasispecies can be mapped into a phenotypic space (fitness landscape) with four different fitness classes and three different peaks [Figure 1(a)]:
-
Peak (W) populated by sequences x0000,0100 (wild-type phenotype and the neutral mutants), with replicative fitness A0000,0100 = 1.
-
Peak (B) populated by sequences x1100,1000 (beneficial mutants plus the neutral mutants), with replication rate A1000,1100 = 1 + sB.
-
Peak (D) populated by sequences x0010,0110 (deleterious mutant and the neutral mutants), with replicative fitness A0010,0110 = 1 − sD.
-
The lowest replication value of the fitness landscape is given by the lethal phenotypes, (L), given by sequences xabc1 = 0, a, b, c ∈ {0, 1}, with replication rate equal to zero.
We refer the reader to Supplementary Information Section S1 which contains all i equations obtained from (1). Sequences with both beneficial and deleterious mutations (given by x0010,0110 and with replication rates A1010,1110 = 1 + sB − sD) will populate fitness peaks (W), (B), or (D) depending on the values of the selection coefficients, sB and sD. Note all fitness classes include the neutral mutants. Equations (1) depend on the parameters μ, sB, sD, λB, λD, λL, λN and δ. We set 0 < sB ≤ 1, to ensure that beneficial mutations always increase replication rates. We also set  (if not otherwise specified) to ensure that mutations are always deleterious, also avoiding a 100% decrease in fitness that would result in a lethal mutant (lethal mutants are explicitly introduced as variables in our dynamical system). Note that for sB > sD, mutants x1010,1110 are fitter than the wild-type string and will be considered as beneficial, while for sB < sD their fitnesses are lower than the wild-type fitness and thus will be considered as deleterious. For combined mutations (i.e., strings carrying two or more types of mutations) we assume additive fitness effects. Although epistatic interactions have been described for RNA viral genomes63, as a first approach we will here use additive fitness effects. Hence, the ranges for these parameters are: μ ∈ (0, 1), sB ∈ (0, 1], sD ∈ [0, 1), λB ≥ 0, λD ≥ 0, λL ≥ 0, λN ≥ 0, λB + λD + λL + λN = 1, δ ≥ 0.
(if not otherwise specified) to ensure that mutations are always deleterious, also avoiding a 100% decrease in fitness that would result in a lethal mutant (lethal mutants are explicitly introduced as variables in our dynamical system). Note that for sB > sD, mutants x1010,1110 are fitter than the wild-type string and will be considered as beneficial, while for sB < sD their fitnesses are lower than the wild-type fitness and thus will be considered as deleterious. For combined mutations (i.e., strings carrying two or more types of mutations) we assume additive fitness effects. Although epistatic interactions have been described for RNA viral genomes63, as a first approach we will here use additive fitness effects. Hence, the ranges for these parameters are: μ ∈ (0, 1), sB ∈ (0, 1], sD ∈ [0, 1), λB ≥ 0, λD ≥ 0, λL ≥ 0, λN ≥ 0, λB + λD + λL + λN = 1, δ ≥ 0.
It is important to notice that Eigen's model describes the dynamics of explicit genome sequences2,3,6. We here simplify the system to sequences where mutations are not nucleotide substitutions but changes involving possible phenotypic transitions. Hence, our sequences are not viral genomes but an abstract representation of the genomes in terms of phenotypic traits (see Ref. 64 for other phenotypic approaches to viral quasispecies). In this sense, the relationship between our modeling approach and true viral genomes becomes obvious from the identification of groups of viral genomes that belong to the same fitness phenotypic classes (i.e, all have the same fitness regardless the specific mutations they carry in their genomes). These phenotypic classes are the entities represented in our model. Furthermore, keeping in mind our goal of exploring the role of the DMFE in quasispecies dynamics and transitions, we necessarily made several simplifying assumptions that allow for an analytical treatment. These assumptions and their limitations are discussed in Supplementary Information Section S1.
Experimental data
In this article we use experimental DMFE data for VSV and TEV as a case study for viral quasispecies. Sanjuán et al.14 generated a collection of single-nucleotide substitution mutants of VSV and evaluated their fitnesses in vitro. They found that the frequencies of the four different fitness classes were (using our notation)  ;
;  ;
;  ; and
; and  . Using a similar experimental approach but in this case measuring fitness effects in vivo, Carrasco et al.15 found that such frequencies for TEV were
. Using a similar experimental approach but in this case measuring fitness effects in vivo, Carrasco et al.15 found that such frequencies for TEV were  ;
;  ;
;  ; and
; and  . To simplify notation, in our model we will use λk instead of
. To simplify notation, in our model we will use λk instead of  . We refer the reader to references 14, 15 for further details.
. We refer the reader to references 14, 15 for further details.
Numerical algorithms
We are especially interested in performing an extensive exploration of the model parameters to address several issues. Our interests here are mainly two:
-
a
Given arbitrary parameters of the model, we desire to compute the population values of beneficial, deleterious and lethal sequences at the equilibrium. Furthermore, as typically the parameters are not well known or, simply, non available, we want to establish the probability that the fraction of sequences of each one of the previous types exceeds some fraction N* (being N* a given fixed population equilibrium value). For this later case, we are mainly interested in quantifying the likelihood of finding parametric scenarios impairing viral sequences success, i.e., parameter combinations generating deleterious and/or lethal phenotypes. To do so, we will use the population scenarios (A), (B) and (C) (defined in the Results Section: Exploration of the parameter space). As mentioned, in all these scenarios we want to have a measure of the fraction of parameters for which these scenarios reach values of population size exceeding a given threshold, N*. The domain
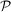 where we locate the parameters is a cube [0, 1]4 corresponding to the values of μ, sB, sD, δ times a three-dimensional simplex Σ3 in the parameters λB, λD, λL, λN with the constrain λB + λD + λL + λN = 1. Different assumptions can be made on the probability density in
where we locate the parameters is a cube [0, 1]4 corresponding to the values of μ, sB, sD, δ times a three-dimensional simplex Σ3 in the parameters λB, λD, λL, λN with the constrain λB + λD + λL + λN = 1. Different assumptions can be made on the probability density in 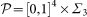 .
. -
b
How fast go the initial conditions (typically the vector x(0) = (1, 0, …, 0)T) to the attractor to which they tend? In other words, what can be said about transients? This is irrelevant if we assume that the evolution time is as large as desired. However, for finite time evolution, T, the distance from x(T) to the attractor can be large.
Let us describe the algorithms to carry out the computations in both cases.
In principle, if we consider a uniform probability density in  to answer question a) amounts to compute the volume of a semi algebraic set in the parameter space. Indeed, let us denote a value of the parameters simply as
to answer question a) amounts to compute the volume of a semi algebraic set in the parameter space. Indeed, let us denote a value of the parameters simply as  . The amount of viral sequences of a given class corresponding to the equilibrium associated with Π can be denoted as g(Π). It is clear, due to the dependence of the matrix A (see Supplementary Inforamtion Section S4) and, hence, of the characteristic polynomial and the eigenvectors, that g is an algebraic function. Therefore the volume of the region of interest in Σ is bounded by the hypersurface g(Π) = N* and boundaries of Σ.
. The amount of viral sequences of a given class corresponding to the equilibrium associated with Π can be denoted as g(Π). It is clear, due to the dependence of the matrix A (see Supplementary Inforamtion Section S4) and, hence, of the characteristic polynomial and the eigenvectors, that g is an algebraic function. Therefore the volume of the region of interest in Σ is bounded by the hypersurface g(Π) = N* and boundaries of Σ.
However, even in the case that g is explicitly available, this is of little use because of the dimensionality. Moreover in the generic case g is not explicitly known. This suggests to use a MonteCarlo (MC) method to compute the volume of interest. The steps are as follows:
-
Using a (pseudo-)random number generator with uniform distribution in [0, 1], we generate four values to obtain a point in [0, 1]4. Then, we generate points with uniform distribution in Σ3 using a standard method.
-
When all the parameters are available we look for the dominant zero of the polynomial pB in Eq. (24) of the Supplementary Information. Let us denote it as σ3 as in Supplementary Information Section S3. Then we proceed to the computation of the components of the fixed point using the formulas (25) and (26) of the Supplementary Information.
-
The process is repeated M times (M large, a typical value being M = 108). Then, for the different values of N* used in the study we count the number of cases c(N*) in which g(Π) ≥ N*. The desired probability is p* = c(N*)/M. In many of our analyses we will represent such a probability as a percentage (i.e., meaning the percentage of parameter combinations driving the quasispecies towards a given scenario for a given value of N*, if not otherwise specified). Alternatively, we can also be interested in transient times (see Results section) and perform a similar analysis considering a given population value for scenarios (A), (B) and (C) at a given time, N(t). Then, the previous probability will be represented as p(t) = c(N(t))/M.
In a large part of the computations the parameter δ is not taken with uniform probability but uniform in log scale, say in the range [δ1, δ2]. Then the value of log(δ) is generated with a uniform distribution in [log(δ1), log(δ2)] and proceed as before.
It can be also interesting to fix δ and proceed in a similar way for a set of values of δ. Then we can recover a probability function p(δ) by interpolation. The desired global probability with respect to a density f(δ) is obtained by integration and normalization

We pass now to the point b). Given parameters Π we can compute the equilibrium x*. On the other hand, we can start the integration of system (3) of the SI from the initial point x(0) = (1, 0, …, 0)T until the current point x(t) reaches a given distance η from x*. Typically we have used the value η = 10−3 and the distance has been computed using the | |∞ norm. The integrations are carried out using the Runge-Kutta-Fehlberg RKF78 method, with automatic step size control and local relative tolerance 10−15. After every step the distance to x* is checked. This allows obtaining the distribution of transient times and the effect of the different parameters on it, with special emphasis on the role of δ as is illustrated below and in the Results section.
Computation of transient times
In order to see how parameter δ, i.e., phenotypic reversion, affects the transients, we carry out the following experiment. For a fixed value of δ we generate a random sample of M* sets of the remaining parameters, as described in Numerical algorithms subsection above. Then, for each set of parameters, the integration of Eq. (2) in the Supplementary Information is started with x(0) = (1, 0, …, 0)T. The integration is stopped when the distance to the fixed point is a small fixed value η. The distance is measured as η = maxi= 1,…,16 |xi(t) − (x*)i|. For a given value τ of the time we record the fraction φ(τ) of M* such that the distance η is reached for a value of t < τ. Then we display φ(τ) as a function of τ (see Figure S8). Of course, for practical reasons, the integration time is limited to a fixed large tmax.
Change history
30 June 2015
A correction has been published and is appended to both the HTML and PDF versions of this paper. The error has not been fixed in the paper.
References
Eigen, M. Self-organization of matter and the evolution of biological macromolecules. Naturwiss. 58, 465–523 (1971).
Eigen, M. & Schuster, P. The hypercycle. A principle of natural self-organization [Eigen, M. & Schuster, P. (eds.)] (Springer-Verlag, Berlin, 1979).
Schuster, P. Evolution on “realistic” fitness landscapes. Phase transitions, strong quasispecies and neutrality. Santa Fe Institute Working Paper #12-06-006, 1–94 (2012).
Domingo, E., Webster, E. & Holland, J. J. Origin and evolution of viruses [Domingo, E., Parrish, C. R. & Holland, J. J. (eds.)] (Academic, San Diego, USA, 1999).
Wilke, C. O. Quasispecies theory in the context of population genetics. BMC Evol. Biol. 5, 44–51 (2005).
Eigen, M., McCaskill, J. & Schuster, P. The Molecular quasi-species. Adv. Chem. Phys. 75, 149–263 (1989).
Domingo, E., Biebricher, C., Eigen, M. & Holland, J. J. Quasispecies and RNA virus evolution: Principles and consequences (Landes Bioscience, Austin, TX, 2001).
Manrubia, S. C., Domingo, E. & Lázaro, E. Pathways to extinction: beyond the error threshold. Phil. Trans. R. Soc. B 365, 1943–1952 (2010).
Franz, S. & Peliti, L. Error threshold in simple landscapes. J. Phys. A: Math. Gen. 30, 4481–4487 (1997).
Satorras, R. P. & Solé, R. V. Field theory for a reaction-diffusion model of quasispecies dynamics. Phys. Rev. E 64, 051909278 (2001).
Saakian, D. B. & Chin-Kun, H. Exact solution of the Eigen model with general fitness functions and degradation rates. Proc. Natl. Acad. Sci. U.S.A. 103, 4935–4939 (2005).
Wright, S. Evolution in Mendelian populations. Genetics 16, 97–159 (1931).
Kauffman, S. & Levin, S. Towards a general theory of adaptive walks on rugged landscapes. J. Theor. Biol. 128, 11–45 (1987).
Sanjuán, R., Moya, A. & Elena, S. F. The distribution of fitness effects caused by single-nucleotide substitutions in an RNA virus. Proc. Natl. Acad. Sci. U.S.A. 101, 8396–8401 (2004).
Carrasco, P., de la Iglesia, F. & Elena, S. F. Distribution of fitness and virulence effects caused by single-nucleotide substitutions in Tobacco etch virus. J. Virol. 81, 12979–12984 (2007).
Saakian, D. B., Muñoz, E., Chin-Kun, H. & Deem, M. W. Quasispecies theory for multiple-peak fitness landscapes. Phys. Rev. E 73, 041913 (2006).
Sardanyés, J., Solé, R. V. & Elena, S. F. Simple quasispecies models for the survival-of-the-flattest effect: the role of space. J. theor. Biol. 250, 560–568 (2006).
Wilke, C. O. Selection for fitness versus selection for robustness in RNA secondary structure folding. Evolution 55, 2412–2420 (2001).
McCaskill, J. S. & Altemeyer, S. Error threshold for spatially resolved evolution in the quasispecies model. Phys. Rev. Lett. 86, 5819–5822 (2001).
Toyabe, S. & Sano, M. Spatial suppression of error catastrophe in a growing pattern. Physica D 230, 1–8 (2005).
Sardanyés, J. & Elena, S. F. Quasispecies spatial models for RNA viruses with different replication modes and infection strategies. PLOS ONE 6, e24884 (2011).
Sardanyés, J. & Elena, S. F. Error threshold in RNA quasispecies models with complementation. J. Theor. Biol. 265, 278–286 (2010).
Iranzo, J. & Manrubia, S. C. Evolutionary dynamics of genome segmentation in multipartite viruses. Proc. R. Soc. B 279, 3812–3819 (2012).
Sardanyés, J., Solé, R. V. & Elena, S. F. Replication mode and landscape topology differentially affect RNA virus mutational load and robustness. J. Virol. 83, 12579–12589 (2009).
Sanjuán, R. Mutational fitness effects in RNA and single-stranded DNA viruses: common patterns revealed by site-directed mutagenesis studies. Phil. Trans. R. Soc. B 365, 1975 (2010).
Eyre-Walker, A. & Keightley, P. D. The distribution of fitness effects of new mutations. Nat. Rev. Genet. 8, 610–618 (2007).
Manrubia, S. C. Modelling viral evolution and adaptation: challenges and rewards. Curr. Op. Virol. 2, 531–537 (2012).
Keightley, P. D. & Lynch, M. Toward a realistic model of mutations affecting fitness. Evolution 57, 683–685 (2003).
Keightley, P. D. The distribution of mutation effects on viability in Drosophila melanogaster. Genetics 138, 1315–1322 (1994).
Loewe, L. & Charlesworth, B. Inferring the distribution of mutational effects on fitness in Drosophila. Biol. Lett. 2, 426–430 (2006).
Imhof, M. & Schlötterer, C. Fitness effects of advantageous mutations in evolving Escherichia coli populations. Proc. Natl. Acad. Sci. U.S.A. 98, 1113–1117 (2001).
Elena, S. F. & Moya, A. Rate of deleterious mutation and the distribution of its effects on fitness in Vesicular stomatitis virus. J. Evol. Biol. 12, 1078–1088 (1999).
van Opiijnen, T., Boerlijst, M. C. & Berkhout, B. Effects of random mutations in the human immunodeficiency virus type 1 transcriptional promoter on viral fitness in different host cell environments. J. Virol. 80, 6678–6685 (2006).
Orr, H. A. The distribution of fitness effects among beneficial mutations. Genetics 163, 1519–1526 (2003).
Antoneli, F., Bosco, F., Castro, D. & Janini, L. M. Virus replication as a phenotypic version of polynucleotide evolution. Bull. Math. Biol. 75, 602–628 (2013).
Perales, C., Iranzo, J., Manrubia, S. & Domingo, E. The impact of quasispecies dynamics on the use of therapeutics. Trends in Microbiol. 20, 595–603 (2012).
Schuster, P. Mathematical modeling of evolution. Solved and open problems. Theory Biosci. 130, 71–89 (2011).
Lorenz, D. M., Park, J.-M. & Deem, M. W. Evolutionary processes in finite populations. Phys. Rev. E 87, 022704 (2013).
Bull, J. J., Meyers, L. A. & Lachmann, M. Quasispecies made simple. PLOS Comput. Biol. 1, e61 (2005).
Bull, J. J., Sanjuán, R. & Wilke, C. O. Theory of lethal mutagenesis for viruses. J. Virol. 81, 2930–2939 (2007).
Wylie, C. S. & Shakhnovic, E. L. Mutation induced extinction in finite populations: lethal mutagenesis and lethal isolation. PLOS Comput. Biol. 8, e1002609 (2012).
Aguirre, J., Buldú, J. M. & Manrubia, S. C. A trade-off between neutrality and adaptability limits the optimization of viral quasispecies. J. Theor. Biol. 261, 148–155 (2001).
Cuesta, J. A., Aguirre, J., Capitán, J. A. & Manrubia, S. C. Struggle for space: viral extinction through competition for cells. Phys. Rev. Lett. 106, 028104 (2011).
Holland, J. et al. Rapid evolution of RNA genomes. Science 215, 1577–1585 (1982).
Holland, J. J., Domingo, E., de la Torre, J. C. & Steinhauer, D. A. Mutation frequencies at defined single codon sites in vesicular stomatitis virus and poliovirus can be increased only slightly by chemical mutagenesis. J. Virol. 64, 3960–3962 (1990).
Loeb, L. A. et al. Lethal mutagenesis of HIV with mutagenic nucleoside analogs. Proc. Natl. Acad. Sci. U.S.A. 96, 1492–1497 (1999).
Anderson, J. P., Daifuku, R. & Loeb, L. A. Viral error catastrophe by mutagenic nucleosides. Annu. Rev. Microbiol. 58, 183–205 (2004).
Grande-Pérez, A. et al. Suppression of viral infectivity through lethal defection. Proc. Natl. Acad. Sci. U.S.A. 102, 4448–4452 (2005).
Chao, L. Fitness of RNA virus decreased by Muller's ratchet. Nature 348, 454–455 (1990).
de la Peña, M., Elena, S. F. & Moya, A. Effect of deleterious mutation-accumulation on the fitness of RNA bacteriophage MS2. Evolution 54, 686–691 (2000).
Duarte, E. et al. Rapid fitness losses in mammalian RNA virus clones due to Muller's ratchet. Proc. Natl. Acad. Sci. U.S.A. 89, 6015–6019 (1992).
de la Iglesia, F. & Elena, S. F. Fitness declines in Tobacco etch virus upon serial bottleneck transfers. J. Virol. 81, 4941–4947 (2007).
Escarmís, C., Lázaro, E. & Manrubia, S. C. Population bottlenecks in quasispecies dynamics. Curr. Top. Microbiol. Immunol. 299, 141–170 (2006).
Yuste, E. et al. (1999) Drastic fitness loss in human immunodeficiency virus type 1 upon serial bottleneck events. J. Virol. 73, 2745–2751 (1999).
Solé, R. V. & Deisboeck, T. S. An error catastrophe in cancer? J. Theor. Biol. 228, 47–54 (2004).
Greaves, M. & Maley, C. C. Clonal evolution in cancer. Nature 481, 306–313 (2012).
Lengauer, C., Kinzler, K. W. & Vogelstein, B. Genetic instabilities in human cancers. Nature 396, 643–649 (1998).
Cahill, D. P., Kinzler, K. W., Vogelstein, B. & Lengauer, C. Genetic instability and darwinian selection in tumours. Trends Cell. Biol. 9, M57–60 (1999).
Fox, M. In vitro mutagenesis by anti-cancer drugs. Chemotherapy 315–322 (1976).
Fox, E. J. & Loeb, L. A. Lethal mutagenesis: Targeting the mutator phenotype in cancer. Seminars in Cancer Biology 20, 353–359 (2010).
Loeb, L. A. Human cancers express the mutator phenotypes: origin, consequences and targeting. Nature 11, 450–457 (2011).
Vogelstein, B. & Kinzler, K. W. Cancer genes and the pathways they control. Nature Medicine 10, 789–99 (2004).
Elena, S. F., Solé, R. V. & Sardanyés, J. Simple genomes, complex interactions: Epistasis in RNA virus. Chaos 20, 026106 (2010).
Reidys, C., Forst, C. V. & Schuster, P. Replication and mutation on neutral networks. Bull. Math. Biol. 63, 57–94 (2001).
Acknowledgements
We thank the members of the Complex Systems Lab as well as Phillip Gerrish, Susanna C. Manrubia and Ernest Fontich for their helpful comments. The authors acknowledge the computing facilities of the Dynamical Systems Group (Universitat de Barcelona). This work was partially funded by the Botín Foundation (JS, RVS), by the Spanish Secretaria de Estado de Investigación, Desarrollo e Innovación grants MTM2010-16425 (CS, RM) and BFU2012-30805 (SFE), by grant 2009-SGR-67 from the Catalan government (CS, RM), by grant NSF PHY05-51164 (JS, SFE) and by the Santa Fe Institute (RVS, SFE).
Author information
Authors and Affiliations
Contributions
J.S. and S.F.E. built the mathematical model. C.S. and R.M. carried out the analysis of the mathematical model and the related theoretical calculations. J.S. and C.S. produced the numerical data. J.S., C.S., R.M. and S.F.E. analyzed the numerical data. J.S., C.S., R.M., R.V.S. and S.F.E. wrote the manuscript. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. The images in this article are included in the article's Creative Commons license, unless indicated otherwise in the image credit; if the image is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the image. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Sardanyés, J., Simó, C., Martínez, R. et al. Variability in mutational fitness effects prevents full lethal transitions in large quasispecies populations. Sci Rep 4, 4625 (2014). https://doi.org/10.1038/srep04625
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep04625
This article is cited by
-
Noise-induced bistability in the fate of cancer phenotypic quasispecies: a bit-strings approach
Scientific Reports (2018)
-
Upper critical field reaches 90 tesla near the Mott transition in fulleride superconductors
Nature Communications (2017)
-
Dynamics and bifurcations in a simple quasispecies model of tumorigenesis
Computational and Applied Mathematics (2017)
-
Abrupt transitions to tumor extinction: a phenotypic quasispecies model
Journal of Mathematical Biology (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.







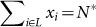 , i.e., sum of the populations of lethal sequences.
, i.e., sum of the populations of lethal sequences.  , i.e., sum of scenarios (A) and (C).
, i.e., sum of scenarios (A) and (C). 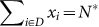 , i.e., sum of the sequences with the deleterious phenotypes, and, if sD > sB, adding also the sequences with both deleterious and beneficial mutations with fitness A = 1 + sB − sD).
, i.e., sum of the sequences with the deleterious phenotypes, and, if sD > sB, adding also the sequences with both deleterious and beneficial mutations with fitness A = 1 + sB − sD). 
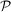 where we locate the parameters is a cube [0, 1]4 corresponding to the values of μ, sB, sD, δ times a three-dimensional simplex Σ3 in the parameters λB, λD, λL, λN with the constrain λB + λD + λL + λN = 1. Different assumptions can be made on the probability density in
where we locate the parameters is a cube [0, 1]4 corresponding to the values of μ, sB, sD, δ times a three-dimensional simplex Σ3 in the parameters λB, λD, λL, λN with the constrain λB + λD + λL + λN = 1. Different assumptions can be made on the probability density in 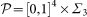 .
.