Introduction

Efficient optical absorbers are highly desired on the microscale where they can play a significant role in preventing crosstalk between optical interconnects on integrated photonic chips. In the thermal spectral region, waste heat is a major energy loss (including thermal radiation loss) in both industrial sectors and our daily life1. Particularly, as the density of integrated circuits in portable electronic/optoelectronic devices increases, on-chip thermal management becomes a critical research topic. To recover thermal radiation energy from objects with varying temperature, an efficient ultra-broadband absorber is an indispensable component. However, it is challenging to realize ultra-compact broadband absorber for on-chip optical, thermal and energy applications. In classic microwave electromagnetic (EM) approaches, EM wave absorbers have long been explored and widely utilized for important military applications, such as improving radar performance and providing concealment against others' radar systems2. In general, however, EM wave absorbers have been limited by their large, bulky dimensions. In recent years, intensive research efforts have been performed to realize compact/portable perfect metamaterial absorbers3. For instance, ideal omnidirectional absorption resonances at microwave, terahertz and mid-near infrared (IR) and visible frequencies have been demonstrated using metamaterial EM absorbers constructed by dielectric thin-films sandwiched by a patterned metal film and a flat metal ground plane3. Due to the critical coupling and/or impedance matching mechanism4,5, a narrow band of incident light can be efficiently coupled to magnetic resonant modes supported in these patterned metal-dielectric-metal metasurface structures. By tuning the geometric parameters of top metal patterns, the narrow band perfect absorption resonance can be tuned freely3. Currently, there is great interest in achieving ‘black’ on-chip metamaterials exhibiting broadband absorption6,7, which is required for thin-film thermal emitters8, thermophotovoltaic cells9 and plasmonic scatterers for photovoltaic cells10,11. Recently, the trapped “rainbow” storage of light was proposed using metamaterials12 and plasmonic graded surface gratings13,14, generating considerable interest for on-chip manipulation of light. In principle, the incident energy will be absorbed if a broadband “rainbow” is trapped in a practical lossy structure. Therefore, the “rainbow” trapping effect will result in a promising platform for an on-chip broadband absorber. However, due to the challenges in achieving broadband metamaterial and/or high quality and high efficiency surface plasmonic structures, limited experimental successes have been reported15,16,17,18. To overcome these limitations faced by metal-dielectric-metal metasurface3 and rainbow trapping structures12,13,14,15,16,17,18, in this study, we report the experimental realization of the patterned hyperbolic metafilm with engineered and freely tunable absorption band from near-IR to mid-IR spectral regions based on multilayered metal/dielectric films. Compared with recently reported compact plasmonic/meta-absorber based on crossed trapezoid grating arrays6 and ultra-sharp convex metal grooves7, the proposed hyperbolic metafilm pattern is superior on its ultra-wide spectral tunability from optical (i.e. visible to near-IR) to thermal (i.e. mid- and far-IR) spectral regions and can be integrated with other on-chip electronic/optoelectronic devices easily. The ability to efficiently produce broadband, highly confined and localized optical fields on a chip is expected to create new regimes of optical/thermal physics, which holds promise for impacting a broad range of energy technologies ranging from photovoltaics, to thin-film thermal absorbers/emitters, to optical-chemical energy harvesting.

Physical mechanism and theoretical modeling

HMM refers to an artificial medium with subwavelength features whose iso-frequency surface is a hyperboloid19,20,21,22,23,24,25. This type of metamaterial (also called indefinite medium19) has a diagonal form of the permittivity tensor (i.e. ε = diag(εx, εy, εz)) whose diagonal elements have different signs (e.g. εx = εy < 0, εz > 0), leading to the hyperbolic iso-frequency surface, i.e. ω2/c2 = kx2/εz +ky2/εz +kz2/εx19,20. This unique feature corresponds to highly anisotropic optical properties (i.e. dielectric in one direction and metallic in other directions), which is promising for a variety of applications, including three-dimensional indefinite cavities26, spontaneous emission enhancement22,53, active nanoplasmonic devices27,28, etc. Recently, an interesting concept was proposed to realize an on-chip ultra-broadband and tunable super absorber in near-IR, mid-IR to microwave domain29,30,31 using patterned HMM waveguide taper arrays constructed by multilayered metal/dielectric thin films. The physical mechanism of this intriguing ultra-broadband absorption was attributed to slow light modes confined in HMM waveguide tapers, leading to the enhanced light-matter interaction and therefore, strong/perfect absorption of the light. Lossless dispersion curves of the HMM waveguide were analyzed to explain the slow-light-based super absorption, which, however, introduced a potential conflict with the proposed super absorption29,31. In this section, we first compare the dispersion curves for lossless and lossy HMM waveguide arrays to reveal the difference between ideally lossless and practical lossy structures and interpret the physical mechanism of the broadband on-chip absorption more accurately. Then, we will discuss the period dependence of the absorption properties of the patterned HMM films.

(A) Light trapping in lossless and lossy HMM waveguide taper arrays

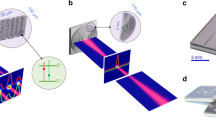
In a latest theoretical work, we analyzed the waveguide modes supported in a single HMM waveguide taper by considering small losses32. As the incident light is coupled into the HMM waveguide taper, the group velocity (vg) of the waveguide mode at different wavelength can be reduced significantly at their corresponding critical widths, leading to the so-called “rainbow” trapping effect in the vertical direction32. It was recognized that a mode conversion occurs between the forward-waveguide-mode (i.e., |f> mode whose power flow is parallel to its propagation direction) and the backward-waveguide-mode near the critical width (i.e., |b> mode whose power flow is anti-parallel to its propagation direction)32. Considering the non-negligible loss and finite geometric changes in practical structures (e.g., tapered width, surface roughness, etc.), the mode propagation details are still largely unexploited. As shown in Fig. 1a, we investigate a HMM pattern array consisting of alternating layers of silver (Ag) and silicon dioxide (SiO2) films surrounded by air (i.e. ε1 = 1). According to the effective medium theory33, when the film thickness of each layer is much smaller than the wavelength, its permittivity tensor can be approximately described as: ε2x = ε2y = fεAg+(1-f)εSiO2, 1/ε2z = f/εAg+(1-f)/εSiO2, where f is the thickness filling ratio of the metal layer. In a HMM waveguide array, its waveguide modes in adjacent units will interact with each other due to the overlap of their evanescent fields. Therefore, the EM field in this periodic structure can be described by the Bloch mode, i.e. F(x+P) = F(x)exp(-ikx0P)34. Here, P is the period of the structure; kx0 represents the momentum along the x-direction of the Bloch mode. Under the normal incident condition, the Bloch mode with kx0 = 0 can be excited. Its propagation constant β can be calculated by Eq.(1):

Here, , , is the vacuum wave vector and w is the width of the HMM layer. The dispersion curves of Bloch modes supported in a periodic HMM waveguide array can be plotted by solving this eigenequation. In this modeling, dispersive optical constants of Ag are considered and the filling factor, f, is 0.538. We set the period of the HMM pattern to P = 1.17 μm and the incident wavelength to λ = 3.5 μm. The width of the HMM waveguide taper increases from 500 nm to 950 nm, with the vertical dimension of 2 μm. In this case, the anisotropic permittivity tensor elements are ε2x = −240.05+40.391i, ε2z = 4.64+0.0042i. As shown in Fig. 1b, the real part, βr and the imaginary part, βi, of the propagation constant at this wavelength are plotted in the upper and lower panels, respectively. Under the lossless assumption, attained by neglecting the imaginary parts of ε2x and ε2z, one can see that a degeneracy point is achieved, connecting the two branches of |f> and |b> modes (see solid curves), as indicated by the arrow in the upper penal of Fig. 1b. According to our previously reported theoretical analysis32, the group velocity is 0 in principle at this degeneracy point, which, however, cannot be reached due to the mode conversion mechanism. Consequently, obvious interference patterns can be observed in the electric field (E-field) distribution confined in the lossless HMM waveguide taper (as shown in Fig. 1c) because of the interference between the |f> and |b> modes. When the real loss of Ag is considered in the modeling (e.g. ε2x = −240.05+40.391i, ε2z = 4.64+0.0042i), the waveguide mode is mainly attenuated in the x direction due to the large imaginary part of ε2x (see Fig. 1d). One can see from Fig. 1d that the intensity of the guided mode inside the HMM taper is significantly lower than that in the lossless case, shown in Fig. 1c. An obvious difference is that the degeneracy point cannot be realized, as shown by the blue and red dotted lines in Fig. 1b. As the ideal degeneracy point is approached, the absolute value of the imaginary part of the propagation constant, βi, increases significantly for the |f> mode (see the red dotted line in the lower panel of Fig. 1b) and remains large when the mode is converted to the |b> mode (see the blue dotted line in the lower panel of Fig. 1b). Therefore, the mode intensity is attenuated strongly as the degeneracy point position is approached, with the simultaneous mode conversion in the lossy HMM waveguide taper array. One can see that the interference pattern shown in Fig. 1d is suppressed as compared with the lossless situation shown in Fig. 1c, indicating the weak intensity of the |b> mode converted from the |f> mode. Based on the understanding of the mode conversion and loss properties of the HMM waveguide taper array, an unambiguous mechanism of the predicted broadband absorption is therefore clarified.

Figure 1
figure 1

Light trapping in lossless and lossy HMM waveguide taper arrays.

(a) Conceptual illustration of HMM waveguide taper arrays constructed by alternating metal-dielectric films. (b) The width-dependent dispersion curve for the propagation constants of λ = 3.5 μm. The real part, βr and the imaginary part, βi are shown in the upper and lower panels, respectively. The lossless curve is plotted by solid curves, with the degeneracy point indicated by the arrow. The dispersion curves with real losses are plotted by dotted curves for the |f> and |b> modes, respectively. (c) and (d) are E-field distributions in the (c) lossless and (d) lossy HMM waveguide tapers for the TM0 modes, respectively.

Full size image

(B) Period dependence

For most periodic grating structures, their optical properties are usually sensitive to the periodicity of patterns. In previously reported theoretical design29,30,31, the period of the array was generally selected based on the bottom width of the HMM waveguide taper. It has not been revealed that how the period selection will affect the absorption properties of the patterned HMM films. To demonstrate the absorption engineering tunability, here we model the one-dimensional (1D) absorption cross-section, σabs, for a single unit of the HMM waveguide taper, which is defined as the power absorbed by the HMM waveguide taper (in the unit of Watt) divided by the incident power density (in the unit of Watt/μm in two-dimensional modeling)35,36. As an example, an 8-pair HMM waveguide taper unit with the top and bottom widths of 550 nm and 1.14 μm, respectively, was analyzed in Fig. 2a. One can see that when the 1D absorption cross-section is larger than the physical dimension of the bottom width (i.e. 1.14 μm, see the dotted line in Fig. 2a), the strong absorption can be obtained within the wavelength range from 2.9 – 5 μm (see the shaded region in Fig. 2), corresponding to two wavelength edges of the absorption band that can be obtained by this pattern array. To validate this prediction, we model the absorption spectra of the HMM waveguide taper array by tuning the period of the patterns. As shwon in Fig. 2b, when the period increases from 1.14 μm (structure A) to 1.35 μm (structure B) and 2.26 μm (structure C), the central position of the absorption band did not change with the period, indicating that the absorption property of the proposed HMM waveguide taper array is mainly determined by the top and bottom width of the HMM waveguide taper rather than the period. The period selection will only affect the profile and intensity of the absorption spectrum. One can see that in the short wavelength side (λ < 2.90 µm), the absorption of structure C (P = 2.26 μm) is generally lower than those for structures A (P = 1.14 μm) and B (P = 1.35 μm) since the absorption cross-section (i.e. 0.06 – 1.16 μm as shown in Fig. 2a) is much smaller than the period of structure C. In addition, the absorption of structure A in the long wavelength side is obviously stronger than the other two samples due to the mode interaction between two ajacent pattern units in the subwavelength scale. According to the modeling results shown in Fig. 2b, the absorption for structure A and C at the wavelength of 5.15 μm are 93% and 45%, respectively. To reveal the difference between these two structures, we plot the normalized E-field distribution at this wavelength, as shown in Fig. 2c for structure C and Fig. 2d for structure A, respectively. One can see that the localized field in structure A is obviously enhanced in the air gap between adjacent HMM waveguide tapers due to the mode interaction (see the white squares in Fig. 2d). This mode interaction within subwavelength scale resulted in the enhanced absorption at longer wavelengths.

Figure 2
figure 2

Period dependence of the HMM pattern array.

(a) 1D absorption cross-section of a single 8-pair HMM waveguide taper unit with the top and bottom widths of 550 nm and 1.14 μm, respectively. The thicknesses of the metal and dielectric films are both 35 nm, respectively. (b) Absorption spectra of three periodic patterns with the period of (A) 1.14 μm, (B) 1.35 μm and (C) 2.26 μm. (c) and (d) are modeled E-field distributions in (c) structure C and (d) structure A at the wavelength of 5.15 μm.

Full size image

Based on the understanding of the optical absorption mechanism and period dependence of the HMM waveguide taper array, in the next section, we discuss the fabrication and characterization to realize the spectrally tunable on-chip broadband super absorptive hyperbolic metafilm from near-IR to mid-IR spectral regions.

Experimental Results and Discussion

(A) Multi-layered HMM waveguide taper array for broadband absorption engineering

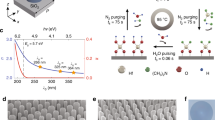
The alternating multi-layered Ag-SiO2 films were deposited in a multi-target electron-beam evaporation system. The thickness of each Ag/SiO2 layer was controlled at 30 nm ± 5 nm. To improve the surface roughness of these alternating layers, 2-nm-thick Ge layers were inserted between Ag and SiO2 layers to enhance the wettability between these two materials37,38,39. In this experiment, we first deposited one-pair Ag/SiO2 layer on top of a 150-nm-thick Al film and fabricated a one-dimensional (1D) patterned meta-absorber using focused ion beam (FIB) lithography, as shown in Fig. 3a (sample 1). The period and width of the top Ag pattern are 950 nm and 720 nm, respectively. Due to the optically opaque ground plane (i.e. the 150-nm-thick Al film), the optical absorption of the structure can be characterized by 1-R where R is the reflection intensity. With x-polarized incident illumination, an absorption peak exceeding 75% was observed experimentally at the wavelength of 3.5 μm, as shown by the solid black curve in Fig. 3b, agreeing well with the numerical modeling result shown by the solid black curve in Fig. 3c. To demonstrate the broadened absorption band based on the proposed HMM waveguide taper, we deposited a 4-pair Ag/SiO2 layer on top of the 150-nm-thick Al film and patterned the waveguide taper, as shown in Fig. 3a (sample 2). The period of the HMM pattern is 1.17 μm and the width of the waveguide taper increases from 500 nm on the top end to 950 nm on the bottom end. As shown by the solid red curve in Fig. 3b, the measured full width at half maximum (FWHM) of the absorption band was broadened to the wavelength range of 2.5 to 4.7 μm, agreeing reasonably well with the modeling result shown in Fig. 3c and covering the narrow band absorption resonance obtained by the 1-pair Ag/SiO2 film structure completely. To further broaden the absorption band, we then deposited 8-pair multi-layers and patterned the waveguide taper array with the period, top width and bottom width of (1.35 μm, 480 nm, 1.14 μm) as shown in Fig. 3a (sample 3). According to the measurement and modeling results shown by solid blue curves in Figs. 3b and 3c, the FWHM of the absorption band can be extended to the wavelength range of 2 to 6.53 μm and 2.70 to 5.52 μm, respectively.

Figure 3
figure 3

Multi-layered HMM waveguide taper array for broadband absorption engineering.

(a) 54°-tilted SEM images of 6 samples of super absorptive meta-films. The period and width of the top Ag pattern of sample 1 are 950 nm and 720 nm, respectively. For samples 2–6, the period, top width and bottom width parameters are (1.17 μm, 500 nm, 950 nm) for sample 2, (1.35 μm, 480 nm, 1.14 μm) for sample 3, (1.57 μm, 850 nm, 1.35 μm) for sample 4, (300 nm, 110 nm, 270 nm) for sample 5 and (1.17 μm, 500 nm, 950 nm) for sample 6, respectively. The scale bar is 500 nm. (b, d, f, h) and (c, e, g, h) show measured and modeled absorption spectra of these 6 samples (indicated by sample number), respectively.

Full size image

Importantly, this broad absorption band is tunable by changing the geometric parameters. For instance, for the 4-pair HMM waveguide taper array, when the period, top width and bottom width were tuned to 1.57 μm, 850 nm, 1.35 μm, respectively (see sample 4 in Fig. 3a), the FWHM of the absorption band was tuned to 3.80–6.03 μm and 4.05–6.00 μm, indicated by the solid black curve in Figs. 3d (measured result) and 3e (modeled result). As shown in Fig. 3f (measured result) and Fig. 3g (modeled result), we also tuned the absorption band to 0.90–2.00 μm by adjusting the period, top width and bottom width to 300 nm, 110 nm, 270 nm based on the 8-pair multi-layers (see sample 5 in Fig. 3a). Furthermore, by extending the 1D tapered structure into the two-dimensional (2D) pyramidal pattern array (see sample 6 in Fig. 3a, in which the period, top width and bottom width are 1.17 μm, 500 nm, 950 nm, respectively), a polarization insensitive absorption band can be realized for normal incident light, as shown by the black dotted (i.e., y-polarization) and blue solid curves (i.e., x-polarization) in Fig. 2h (measured result) and the black curve in Fig. 3i (modeled result). According to the mode distribution analysis shown in Fig. S1 , these observed tunable broadband absorption is contributed by the vertically trapped resonances, as we predicted in Fig. 1 theoretically. A noticeable difference can be observed between experiment and modeling results as the layer number increases, mainly due to the imperfect quality of the multi-layered films, surface roughness (see Fig. S2 for details) and fabrication errors of the patterns (see Fig. S3 for details). It was believed that the scattered light will couple stronger to the high-k modes of roughened HMM structures constructed by nanowire arrays40. However, as we explained in Fig. S4 in the supplementary materials, when the incident light is within the resonance wavelength band of the proposed multi-layered HMM waveguide taper, the roughness near the degeneracy point will reduce the peak absorption. Scattering of these defects lead to the reduced coupling efficiency of the resonant mode supported by the HMM waveguide tapers.

According to a recent experimental report, tapered/pyramidal patterns with fixed side-wall angle of 75° were manufactured using electron-beam lithography and lift-off processes, which was not desired for the original design of those reported indefinite cavities based on HMM waveguide patterns26. On the other hand, this intrinsic tapered/pyramidal structure should provide a better surface roughness on side walls to improve the quality of the pattern, which is still under optimization. Nevertheless, the systematic experiment and modeling results presented in Fig. 3 demonstrate the feasibility and spectral tunability of the proposed super absorptive hyperbolic metafilms. It should be emphasized that the ultra-broadband absorption tunability is a remarkable feature of the proposed patterned hyperbolic metafilm compared with previously reported compact plasmonic/meta-absorbers in visible to near-IR spectral regions6,7. However, an obvious challenging to realize the proposed hyperbolic metafilm pattern is the quality control and improvement for the multi-layered metal/dielectric films. For instance, 20 and 15 pairs of metal/dielectric thin films were required to realize the broadband absorption band from mid-IR29 to near-IR spectral regime30, respectively, which is extremely challenging to maintain the flat and continuous films in practice. In the next section, we discuss a multi-pattern design to minimize the required number of layers without sacrificing the absorption bandwidth and extend the proposed HMM multi-layers to thinner hyperbolic metasurfaces.

(B) Multi-unit pattern array based on less metal/dielectric films

In recent years, multiple top pattern units with different dimensions in a single period were fabricated to support different magnetic resonances and therefore broaden the absorption band of single-paired planar meta-absorbers41,42,43,44. An ideal broadband absorption resonance requires an optimized selection of period and width, which is difficult to obtain due to the limited tunability of the pattern width within a given period. In addition, the bandwidth cannot be broadened unlimitedly due to the finite period space, leading to a trade-off between the absorption peak and its bandwidth41,42,43,44. To address the intrinsic limitation imposed by the single-paired meta-absorber design, graded metal-dielectric patterns were stacked in the vertical direction as we demonstrated in the previous section and therefore largely released the restriction of the pattern width tunability. By introducing tapered or pyramidal multi-layered patterns in a single period, the width of the metal-dielectric layer-pair can be freely tuned within the given period. In this case, multiple resonant absorbers with finely tuned dimensions are cascaded in a single unit, leading to a significantly broadened absorption band. Unfortunately, many more pairs of metal/dielectric layers are required to realize broader absorption bands, which is challenging in practice, as we explained in Fig. 3 and Fig. S2 . Here we combine the multi-unit pattern array proposed for single-paired perfect absorber and the multi-layered HMM waveguide taper in a single structure to minimize the required number of layers and realize an ultra-broad absorption band.

As shown in Figure 4a (sample 7), a 2-unit HMM waveguide taper array was fabricated on the 4-paired Ag/SiO2 film. The period of the pattern unit is 2.26 μm and the top and bottom widths of two units increase from 580 nm to 860 nm and from 790 nm to 1.2 μm, respectively, similar to the width range of the tapered structure fabricated on the 8-paired Ag/SiO2 film shown in Fig. 3a (sample 3, from 480 nm to 1.14 μm). One can see that the FWHM of the absorption band ranges from 2.50 μm to 5.57 μm in experiment (see the solid black curve in Fig. 4b) and from 2.90 μm to 5.31 μm in modeling (see the black curve in Fig. 4c), which is equivalent to the one achieved by sample 3 in Fig. 3a. Considering the obvious geometrical difference between sample 3 and sample 7 (i.e. the spatial discontinuity between the two graded patterns and different period), the absorption band of sample 7 is slightly narrower than that for sample 3 due to the larger period, which was already predicted in Fig. 2b. To interpret this remarkable absorption property, we model the mode distribution in this 1D two-pattern system as shown in Fig. 4d. One can see that different wavelengths are trapped at different positions in these two patterns, similar to the light trapping phenomenon obtained in the single unit HMM pattern array (i.e. sample 3) as shown in Fig. S1 . It should be noted that the dimension of these two patterns was designed with an overlap (i.e. the widths of the bottom and top of the small and large patterns are 860 nm and 790 nm, respectively) so that the potential effect of the discontinuity between the bottom and the top of the two patterns can be minimized (see Fig. S5 for details). As shown by the second panel of Fig. 4d, the wavelength of 3.8 μm is trapped in both small and large patterns. Furthermore, the polarization dependence of these 1D pattern arrays can be overcome by introducing 2D distributed multi-unit patterns, as shown in Fig. 4a (sample 8). In this fabrication, the periods along two directions are both 2.26 μm and the square pyramidal widths of the four units increase from 630 nm – 860 nm (i.e. a1-a2) and 790 nm – 1.20 μm (i.e. b1-b2), respectively. In this case, a polarization insensitive absorption band is obtained with an FWHM from 2.60 μm to 5.56 μm. The slight wavelength mismatch between the two polarization responses (see dotted lines in Fig. 4b) is introduced by the fabrication error along the x and y directions. As shown in Fig. 4e, the cross-sectional mode distribution along x or y direction is plotted using three-dimensional modeling, confirming the polarization-insensitive vertical “rainbow” trapping phenomenon in the 2D hyperbolic metafilm patterns. Importantly, the required number of metal/dielectric layers is reduced by half, therefore simplifying the sample preparation and experimental realization of the on-chip broadband super absorptive metafilms significantly. Although the structure reported in this article was fabricated using FIB milling technique, the multi-patterned structure is promising to be extended to a larger scale based on recently reported nanofabrication methods including micro/nanosphere mask lithography and nano/micro-stencil patterning45,46 and will enable the development of practical optical/thermal technologies.

Figure 4
figure 4

Multi-unit HMM waveguide taper array for broadband on-chip absorber based on less metal/dielectric films.

(a) 54°-tilted SEM images of super absorptive meta-films with multiple patterns in a single period. For sample 7, the period is 2.26 μm. The top and bottom width parameters are (580 nm, 860 nm) and (790 nm, 1.2 μm), respectively. For sample 8, the period is 2.26 μm. The square pyramidal widths of the four units increase from 630 nm–860 nm (i.e. a1-a2) and 790 nm –1.2 μm (i.e. b1-b2), respectively. The scale bar is 500 nm. Images (b–c) show measured and modeled absorption spectra of these 2 samples, respectively. For comparison, the measured and modeled absorption spectra of sample 3 with 8-pair Ag/SiO2 layers are plotted by solid red curves. (d) and (e) are modeled E-field distributions in the (d) 1D two-pattern structure and (d) 2D four-pattern HMM waveguide taper structure. The cross-sectional mode distribution shown in (e) is modeled along the x or y axis with corresponding x- or y-polarized incident light.

Full size image

In conclusion, due to the strong attenuation during the mode conversion process occurring in the HMM waveguide constructed by metal/dielectric multi-layers, the super absorptive hyperbolic metafilm is realized with the tunable absorption band in near, mid and far IR spectral regions. By cascading resonant metal-dielectric-metal perfect absorber elements with gradually tuned widths along the vertical direction, the absorption band of the patterned HMM film is extended significantly. Multi-patterned HMM metafilms have been demonstrated to reduce the required number of metal/dielectric layers and therefore simplify the sample preparation and experimental realization of on-chip broadband super absorbers. This work will pave the way towards future investigations of a broad range of energy technologies, such as solar photovoltaics10,11, thin-film thermal absorbers/emitters8 and plasmon-mediated surface/localized photocatalysis47. In addition, the spatial control of the localized dispersion properties of multi-layered HMM patterns can also provide a practical platform for prolonged light-matter interactions48. Importantly, the thickness and width of each layer can be controlled to finely engineer the absorption profile to mimic absorption properties of other materials for novel stealth/camouflage applications. In addition, according to Kirchhoff's law of thermal radiation, the emissivity of a material is equal to its absorptivity at equilibrium. Due to the spectrally tunable slow-light principle, the effective refractive index of the super absorptive hyperbolic metafilm pattern is very large, particularly for mid-far IR wavelengths, which is not naturally available. Therefore, being able to create a high index super absorptive/emissive material for mid-far IR wavelengths will provide a technological foundation for a variety of thermal applications, including extraction of more thermal energy from a more compact thermal emitter49, miniaturizing the dimension and improving the performance of conventional heat-to-light converters, thermophotovoltaic cells and radiative coolers/heaters50. This absorption engineering will lead to the development of controllable, effective media and improve our ability to manipulate light in man-made metasurfaces that do not exist in the natural world51.

Methods

Numerical modeling

The absorption profiles of all patterned multi-layered structures shown in Figs. 2 and 3 were modeled using a commercial modeling package Rsoft® based on rigorous coupled wave analysis, which expands the electromagnetic field into 30 and 10 × 10 diffraction orders for 1D and 2D simulations, respectively. The mode distributions shown in Fig. S1 and Fig. 3 were modeled using COMSOL® based on finite element method. The dispersive optical constants of Ag and Al52 were employed in the modeling. The refractive index of SiO2 is 1.46.

Sample preparation and fabrication

The alternating multi-layered metal/dielectric films were deposited in a multi-target electron-beam evaporation system (BOC Edwards Auto 500 system and AJA sputtering/e-beam evaporation dual chamber hybrid thin film deposition system). All patterned hyperbolic metafilm structures were fabricated using a focused ion beam milling system (Zeiss CrossBeam® Workstation system). To obtain reasonably good fabrication quality, the milling current was set to 120 pA. The fabrication area of each sample was 50 μm × 50 μm.

Characterization

The reflection/absorption spectra of patterned hyperbolic metafilms were characterized using a microscopic Fourier transform infrared spectroscopy (Bruker, VETEX 70 + Hyperion 1000). The wavelength range of this system is 450 nm ~ 28.5 μm. The observation area for each sample was set to 50 μm × 50 μm. Two linear polarizers in the visible-IR (i.e. Thorlabs, LPNIR100, 650 nm to 2 μm) and mid-far IR (i.e. Thorlabs, WP25H-K, 2 μm to 30 μm) were used to control the polarization state of the incident light in the characterization, respectively. It should be noted that the numerical aperture of the 15X objective lens is 0.4, which can only collect the scatter light within an angle of 23.6°. It is very difficult to characterize the absorption of small area structures accurately if the scatter light is beyond this collection angle. Fortunately, according to the modeling analysis shown in Fig. S6 , the zero-order reflection spectra from all 8 samples are identical to their total reflection spectra, indicating that higher order reflection/scattering signal is negligible. Therefore, the measured absorption spectra reported in this article are reliable compared with their corresponding numerical modeling results.