Introduction

Active transport is critical in maintaining biological functions in living cells1. This is especially true in neurons where axons and dendrites have long aspect ratio geometry, which limits the effectiveness of passive diffusion. Cargo transport in cells is mediated by a stochastic interplay of passive diffusion and active transport2. Passive diffusion occurs when particles are moving randomly through the viscoelastic subcellular space3. Passive behavior resembles Brownian motion where the mean squared displacement is proportional to time (MSD ∝ Dτ). Active transport is directed motion along cytoskeletal structures that is driven by molecular motors4. Active behavior resembles directed motion where the mean squared displacement is proportional to the square of time (MSD ∝ V2τ2). Thus by measuring how the MSD of vesicles scales with time it is possible to determine their mode of transport5,6. Fig. 1a,b shows a representative image and a schematic of a vesicle switching between active transport along a microtubule and passive diffusion in the subcellular space. This process allows the neuron to control the spatial organization of vital proteins and molecules throughout its complex structures. As an example, if a synaptic protein is synthesized in the cell body, it may need to be transported the entire length of the axon (which could be over 1 meter in a human) to reach its functional target. Thus active transport of specific subcellular cargo can be used to target different locations in the neuron7.

Figure 1
figure 1

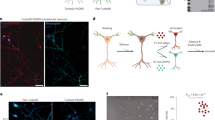
Vesicles switch stochastically between active and passive transport states.

(a) A representative image of an Aplysia neurite showing vesicles of varying size (example image sequence available in supplementary information, video S1). (b) Simplified schematic of vesicle transport in a neurite. Vesicles alternate between active transport along microtubules and passive brownian-like motion. Mechanical strain is applied to modulate tension along neurite length and vesicle dynamics are tracked. (c) Plot of a representative trajectory, where the tMSD algorithm is used to determine active (α ≥ 1.4) and passive motion (α < 1.4). This example clearly shows the vesicle switching between active and passive behavior. The inset shows the slope of the average MSD for active (green) and passive (red) vesicle motion for the trajectory shown. (d,e) Plots of the x and y position as a function of time show that particle behavior is passive (red) most of the time and that when vesicles undergo active motion (green) they are moving over larger distances.

Full size image

Investigating the mechanisms of neuronal transport is critical in understanding neuronal function. Proper transport of vesicles and their cargo to specific locations in the cell is critical in building and maintaining synaptic machinery as well as modulating synaptic plasticity8. For instance, preassembled units of synaptic proteins are transported in vesicles to synapses to provide building blocks for the active zone, which is necessary for rapid fusion of synaptic vesicles7. And activity-dependent synaptic plasticity involves rapid recruitment (under 10 min) of synaptic vesicles associated with synaptophysin to the presynaptic terminal9. Additionally, a deficit in neuronal transport is an early pathogenic event and possibly the cause of several neurodegenerative diseases10,11.

Mechanical tension exists in neurons and stretch growth of axons is critical during developmental stages12,13,14. Recently tension has been implicated in maintaining normal vesicle dynamics6,15,16, but the underlying mechanism is not well understood. The relationship between neuronal stretch and vesicle transport has not been directly investigated. To this end, we analyzed active transport of endogenous large dense core vesicles of in vitro Aplysia neurons under external mechanical strain and quantified their dynamics using tools from statistical physics. We used a stretchable substrate to apply tensile or compressive strain to cultured Aplysia neurons17 and recorded vesicle dynamics via high-speed video microscopy. Vesicle trajectories were tracked and analyzed using a temporal Mean Squared Displacement (tMSD) analysis to quantify active and passive transport6. Active vesicle motion was used to investigate directed motion driven by molecular motors and passive motion was used to estimate the effective diffusivity of vesicles in the cytoplasm.

Results

Measuring active transport of vesicles

Vesicle motion is characterized as active or passive depending on the persistent directionality of its trajectory. To quantify vesicle dynamics the tMSD method is used as described previously6. A representative image, schematic diagram and experimental data of the motion of a vesicle in a neurite is shown in Fig. 1 (see supplementary video S1). The tMSD analysis gives a measure of the distance a vesicle travels from an initial location during time τ and α is the slope of the MSD(τ). α = 1 for Brownian motion and α = 2 for a vesicle moving at a constant speed. The tMSD can be plotted for the vesicle at any time during its journey as a means to investigate whether it is moving actively or passively by evaluating its α at that time. In our analysis, we use τ on the interval 100–160 ms to determine α. Furthermore, we consider motions with α ≥ 1.4 as active based on calibrations from experiments and Brownian simulations.

The measured trajectory of a vesicle is color coded to illustrate the stochastic switching between active (αactive ≥ 1.4, green) and passive (αpassive < 1.4, red) states (Fig. 1c–e). This experimental data is an example showing that a vesicle undergoing active transport moves directionally and over longer distances compared to vesicles undergoing passive motion. In addition, when a vesicle is being actively transported it moves at a higher velocity as indicated by the steeper slope of the green data points (Fig. 1d,e). It should be noted that Aplysia bag cell neurons have vesicles ranging in size from 30 nm to nearly 1 μm18. Vesicles were defined as large or small based on the median vesicle size r ≈ 350 nm measured from the images, however size determination of many tracked vesicles may be diffraction limited.

Probability of active motion increases due to stretch

To quantify the amount of active transport the probability of active motion, Pa, is estimated from each image sequence by dividing the time of active vesicle motion, tactive, by the total tracked time, ttotal,

where indicates an average over all cells and vesicles. In control neurons (Fig. 2, red), the probability of active motion is steady and remains ~0.09. This value is similar to the probability of active motion observed for tracer beads in a remodeling actin-myosin gel19. To create a remodeling gel, Stuhrmann et al.19 reconstituted a network of actin with cross-links and myosin II filaments, resulting in a gel driven out of equilibrium by polymerizing actin and myosin motors. The myosin motors move actin filaments that interact nonspecifically with tracer beads giving rise to active motion. As the gel network continues to remodel it approaches an equilibrium state where tracer beads no longer exhibit active motion, but instead resemble stationary beads in an elastic gel19. In the neuron the subcellular structure is relatively stable and significant reorganization is not expected, yet it maintains dynamics similar to a far from equilibrium remodeling actin-myosin gel. This may be due to the fact that vesicles in the neurons are being driven directly by molecular motors whereas tracer beads in the actin-myosin gel are moving via nonspecific interactions.

Figure 2
figure 2

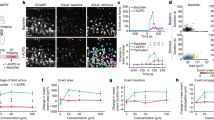
Active transport of vesicles increases due to stretch.

Probability of active motion of vesicles in control (red) neurons exhibit stable behavior with Pa,control ≈ 0.09. Under stretch (blue), vesicles exhibit more active motion, which peaks at Pa,stretch ≈ 0.18 after 25 min. The activity of small (×) vesicles remains high whereas large (□) vesicle activity decreases. Vesicles in compressed (green) neurons exhibit slightly decreased activity relative to the control (red). [control (red), stretch (blue), compress (green), all vesicles (○), large vesicles (□), small vesicles (×)]. Solid color-coded lines indicate loading profile of experiments. (n > 19 animals, > 200 vesicles per cell).

Full size image

In stretched neurons (Fig. 2, blue), Pa,stretch increases sharply and peaks at ~0.18 after 25 min of stretch. Interestingly, after 25 min, Pa,stretch begins to decay for large vesicles (rlarge > 350 nm) but remains elevated for small vesicles (rsmall < 350 nm). In compressed neurons, Pa,compress decreases slightly to ~0.07 for vesicles of all sizes and remains low for the duration of the experiment (Fig. 2, green). It is interesting that in all cases the small vesicles (×) consistently have a higher probability of active motion when compared to large vesicles (□). It is possible that the smaller vesicles experience less resistance to motion compared to large vesicles since they may encounter fewer obstacles due to their decreased size. Overall, this data suggests that vesicles spend more time undergoing active transport when a neuron is stretched.

The relation between active transport of vesicles and mechanical stretch may be due to alterations in microtubule structure. Mechanical stretching may stabilize microtubules43 and compression (or stretch release) may induce bending and breakage44. This structural change could modify the kinetic on and off rates of molecular motors leading to a change in active transport. In addition, the slow change (20 min) in probability of active motion may be due to signal transduction cascades induced by stretch activated ion channels45.

Effective diffusion of vesicles increases due to stretch

By quantifying how the velocity of a specific vesicle changes over time, it is possible to estimate its effective diffusion coefficient. One method of quantification is to look at the velocity autocorrelation function of a vesicle, which provides insight on how the vesicle is interacting with its surrounding environment20. The normalized velocity autocorrelation function, ψ(τ), is defined as

where v is the vesicle velocity and t0 is an arbitrary point in time. For a completely non-interacting system where vesicles move at constant speeds independent of τ and 〈v(t0) · v(t0 + τ)〉 = 〈[v(t0)]2〉, we find ψ(τ) = 1. This is not expected in a biological environment due to interactions between the vesicle and the crowded subcellular environment and ψ(τ) exhibits a decay. Thus the rate of decay of ψ(τ) is a measure of how quickly the vesicle velocity decorrelates. Accordingly, the self diffusion coefficient can be evaluated from the integral of the velocity autocorrelation function, , which is known as a special case of the Green-Kubo relations for obtaining transport coefficients20.

We choose a subset of vesicles that undergo primarily passive dynamics (α < 1.4) over long periods (30 s) of time to quantify ψ(τ) and evaluate Ds. More than 90% of the 30 s time, each vesicle undergoes passive motion. We assume that during this Brownian type motion, the vesicles are not driven by any motors and that the media around them is homogeneous and isotropic. In control neurons, ψ(τ) shows a characteristic decay and a self diffusion coefficient, Ds,control ≈ 2 × 10−3 μm2/s (Fig. 3a). When the neuron is stretched, ψ(τ) shows a slower decay, indicating less resistance to motion and a higher self diffusion coefficient, Ds,stretch ≈ 5 × 10−3 μm2/s (Fig. 3b). Under compression, the behavior of ψ(τ) decays slightly more rapidly than the control and Ds,compress ≈ 1 × 10−3 μm2/s. These results show that the self diffusivity of the vesicle increases when the neuron is stretched and decreases due to compression. Interestingly, this may suggest that a microstructural change has occurred during stretching that allows vesicles to move with less resistance.

Figure 3
figure 3

Self diffusivity of passive vesicles increases due to stretch.

(a) Vesicles in control neurons exhibit a characteristic decay of ψ(τ) and Ds,control ≈ 2 × 10−3 μm2/s. (b) When neurons are stretched, vesicles exhibit a slower decay of ψ(τ) and thus have a higher estimated self diffusion coefficient of Ds,stretch ≈ 5 × 10−3 μm2/s. (c) Under compression, vesicles in neurons exhibit behavior similar to the control case. The estimated self diffusion coefficient is slightly lower, Ds,compress ≈ 1 × 10−3 μm2/s. Here, a subset of vesicles that maintain passive motion for most of the time span used (~30 s) are considered in the analysis.

Full size image

Vesicle mobility increases due to stretch

We now can estimate the mobility of vesicles during active and passive motion. During passive motion, the thermal motion of the vesicles is resisted by drag from the cytoplasmic environment. A balance of thermal and drag forces gives Ds = μkBT20, where the mobility is μ = V/F (velocity/drag resistance). From our measured Ds, we get an effective μ = Ds/kBT for the passive states as μcontrol = 0.5 μm/pN·s in control neurons, μstretch = 1.25 μm/pN·s in stretched neurons and μcompress = 0.25 μm/pN·s in compressed neurons. Thus, vesicle mobility increases by 2.5 times when the neurons are stretched compared to control. Under compression, mobility decreases by half.

Overall vesicle motion increases due to stretch

One method to quantify the overall motion of the vesicles is to calculate the average mean squared displacement, , where indicates an average over all available time steps and all vesicles. Fig. 4a indicates the average MSD behavior in control neurons which is relatively constant in time. When neurons are stretched, the overall motion of vesicles increases significantly exhibited by an increase in the MSD. This effect is greatest at t ~ 25 min after stretch has been applied and is most noticeable at large timescales, τ > 10 sec (Fig. 4b). Conversely, when neurons are compressed (Fig. 4c), the MSD decreases, exhibiting significantly decreased motion for all timescales, τ.

Figure 4
figure 4

Overall motion of vesicles increases due to stretch.

(a) Control neurons indicate normal behavior of vesicle motion in neurons over available timescales. (b) When neurons are stretched, the MSD increases significantly and is most noticeable after 25 min of applied stretch and at large timescales, τ. (c) When compressed, the vesicle MSD decreases significantly immediately after compression and remains decreased for the duration of the experiment.

Full size image

Molecular motor activity increases due to stretch

To investigate the dynamics of vesicle motion it is useful to look at the distribution of vesicle displacements as a function of timescale. This is calculated by first choosing a timescale, τ and then building a frequency histogram of Δx(τ). From this we may calculate the probability distribution of vesicle displacements,

and by normalizing the histogram such that . The probability distribution, P(Δx, τ), also known as the Van Hove Correlation function (VHC), is a powerful tool for interpreting vesicle dynamics. The shape of the VHC can provide information on the nonequilibrium dynamics of the system21.

The VHC for particles undergoing Brownian motion in a fluid remains Gaussian at all times τ21, although the width of the Gaussian distribution may increase with τ. However, if a small fraction of the particles in the ensemble occasionally take longer athermal jumps due to active transport (for example, by an external agent), then the histogram of Δx(τ) shows deviation from Gaussian22. For example, in active actin-myosin gels, the VHC of embedded probe particles exhibits a broader Gaussian regime and marked non-Gaussian tails19. The broader Gaussian region has been attributed to the collective action of many motors19 and the non-Gaussian tails suggest the action of a single motor22. For a passive actin gel, the VHC is expected to be mainly Gaussian22.

The results of the calculated VHC's and Gaussian fits of vesicle displacements are shown in Fig. 5, where active and passive behavior were separated using the tMSD analysis (αactive ≥ 1.4 and αpassive < 1.4)6. Here, we again choose subsets of vesicles that undergo primarily passive and primarily active states. Vesicles of each subset spend more than 90% of the time in their respective mode of motion (active or passive). The statistics of the Gaussian fit are shown as . A non-zero mean, , of the distribution indicates a bias in vesicle motion. The standard deviation, σ, is a measure of the Gaussian width and is indicative of collective molecular motor activity19. A non-Gaussian parameter is defined as,

which is a dimensionless parameter that is zero for a Gaussian distribution but takes on non-zero values to characterize deviation from Gaussianity and provides a measure of single motor activity22. The VHC functions are plotted where the subscript “a” indicates active vesicles and the subscript “p” indicates passive vesicles (Fig. 5).

Figure 5
figure 5

Molecular motor activity increases due to stretch.

Here , where is the mean and σ the standard deviation of the Gaussian fit and ξ is the non-Gaussian parameter. The subscript “a” indicates data for active vesicles and “p” are passive vesicles. (a) Vesicles in control neurons exhibit no significant bias () and small values of the ξ for both active and passive vesicles at all timescales. (b) When neurons are stretched the activity of vesicles increases. At short timescales (τ = 0.15 s), ξ increases for active and passive vesicles, indicating an increase in activity possibly due to single molecular motors. At intermediate timescales (τ = 1 s), σstretch > σcontrol indicating an increase in the activity of collective molecular motor ensembles and suggesting a retrograde bias of vesicle motion. The zoomed inset shows the local minima in the distribution indicating a lower probability for a vesicle to stay stationary. At large timescales (τ = 5 s), ξ values are low suggesting little influence from single motor activity and μ values remain large suggesting increased activity of collective motors and a retrograde bias. The probability of retrograde motion of active vesicles was estimated as pr,stretch(τ = 5 s) = 0.59 whereas for all other cases no bias was observed (pr ≈ 0.5). (c) When neurons were compressed, vesicle activity decreased overall for all timescales as indicated by decreased values of σcompress and ξcompress in comparison to the control.

Full size image

Overall, in all experimental conditions and at all timescales observed, σa > σp and ξa < ξp. The larger Gaussian width, σa, observed in active motion suggests active transport is due to a collective ensemble of many molecular motors19. The larger non-Gaussian parameter, ξp, observed in passive motion suggests that a few vesicles are undergoing occasional athermal jumps, possibly from single molecular motors22. The duration of such motions (jumps) is shorter than the time scale (160 ms in the tMSD analysis) used to identify the state of their dynamics and thus the vesicles become labelled as passive.

When neurons are stretched, ξstretch > ξcontrol (for τ = 0.15 and 1 sec), suggesting increased activity of single molecular motors. In addition, σstretch > σcontrol (for τ = 1 and 5 sec), suggesting higher activity of molecular motors giving rise to greater vesicle motion. It is worth noticing, that for stretched neurons the VHC at τ = 1 sec (Fig. 5b, zoomed inset) exhibits a local minima at Δx ≈ 0, indicating that active vesicles are more likely to move than stay stationary. When neurons are compressed, they exhibit the opposite behavior: decreased motor behavior at all timescales. This result suggests that molecular motor activity increases in neurons due to stretch, which has been hypothesized to lead to significantly enhanced reaction kinetics in axonal structures23.

Mechanical stretch induces a retrograde bias in vesicle motion

Control neurons show no significant bias in vesicle motion (), but when neurons are stretched they show a retrograde bias of vesicle motion () at larger timescales. This is most clear in the stretched neuron at τ = 5 sec (Fig. 5b), where the VHC is clearly not symmetric and the distribution has a negative mean, indicating a bias towards retrograde movements. To quantify the bias we estimate the probability of retrograde motion as, . In all experimental conditions, except stretched neurons, we see no significant bias, pr ≈ 0.5. However, for stretched neurons we see pr,stretch(τ = 5 s) = 0.59 for active vesicles, indicating there is a significantly larger probability for vesicles to move in a retrograde direction. The retrograde bias emerges at long timescales, suggesting it is a result of coordinated activity of many molecular events. In axons, retrograde motion of the cargo is due to dynein motors (moving towards the (−) end of the microtubules). Since, vesicles are moved by a cooperative activity of both dynein and kinesin motors engaged on the same vesicle1, a net retrograde motion of vesicles in stretched axons suggests a shift in the balance between dynein and kinesin.

The dependence of μ and ξ on timescale is expected because of the type of phenomenon being measured. The bias and collective activity (measured by and σ respectively) of vesicle motion are processes that require a large number of molecular interactions. Thus their behavior emerges over longer periods of time. The activity of single molecular motors (measured by ξ) are single (short) events which are evident at short timescales, but are averaged out at over longer timescales. Hence, changes in μ are more noticeable at long timescales and ξ at short timescales.

Discussion

Mechanical tension in neurons has been implicated in the processes of growth, development and signaling24,25,26. Normal vesicle transport plays critical roles in many different processes. Here we will briefly discuss two topics: neurodegenerative disease and synaptic machinery.

Deficits in axonal transport are early pathogenic symptoms and possibly causes of several neurodegenerative diseases, including Alzheimer's disease, Parkinson's disease and amyotrophic lateral sclerosis (ALS)10. For instance, in ALS mice, one of the earliest observed pathologies is a decrease in retrograde transport11 that eventually leads to axon degeneration. If external forces can modulate active transport of vesicles in neurons, it may be possible to apply tension to ALS axons (via biochemical or mechanical manipulation) to increase active transport as well as induce a retrograde bias to restore normal axonal transport and prevent degeneration. However, to understand this process it is necessary to study different types of neurons and their sensitivity to strain rate and magnitude.

In neurons, the basis of synaptic plasticity is a change in synaptic strength in response to stimuli and it is believed to be a critical process in mediating the storage of memory in animals27. Synaptic plasticity is partially regulated by the amount of neurotransmitter released at the presynaptic terminal28. Neurotransmitter release is a cyclic process involving transport of vesicles to active zones, clustering of vesicles at the presynaptic terminal, exocytosis of neurotransmitters via vesicle fusion and retrieval and recycling of vesicle membrane after release7,8. Mechanical tension plays a role in many of these processes. Neurons regulate their membrane tension29,30 and increased tension increases the probability of exocytosis and release31,32,33. Axonal tension is critical in maintaining clustering of vesicles at the presynaptic terminal and axonal stretching leads to a further increase in vesicle clustering15,16. It is hypothesized that increased tension leads to actin polymerization in the synapse, which results in greater actin-synapsin binding sites for vesicles to remain localized at the presynaptic terminal9,34,35. However, with increased neurotransmitter release under tension36,37, the available supply of vesicles may become depleted. Our results indicate that neuronal tension modulates the active transport of vesicles in neurons by increasing activity of molecular motors and increasing the effective self-diffusivity of the cargo. Interestingly, this process occurs on the same timescale as synaptic potentiation in Aplysia neurons9. This is a plausible mechanism to increase delivery of vesicles (containing neurotransmitters and other synaptic machinery) to the presynaptic zone to provide the building blocks for structural plasticity, increase the available pool of neurotransmitters and maintain a sufficient supply during elevated release. The emerging scenario is that mechanical tension in neurons increases vesicle transport, presynaptic clustering and neurotransmission; all of which are critical in the process of synaptic plasticity.

Conclusion

Our results suggest that mechanical stretch leads to increased active transport of vesicles in neurons. The increase in active transport could contribute to tension dependent presynaptic clustering15,16 and support tension induced neurotransmission36,37. Neurons regulate their internal tension and this may be a key element in maintaining proper function. Thus, mechanical tension could serve as a robust and simple signal to coordinate biophysical processes critical to neuronal function.

Methods

Cell culture

Aplysia bag cell neurons were isolated and cultured as in previous studies38. A. californica were obtained from the National Resource for Aplysia (University of Miami/RSMAS, Miami, FL, USA). Neurons were mechanically dissociated from the Aplysia CNS after a 30–60 min incubation in 1% protease. Cells were plated in artificial sea water antibiotic solution on fibronectin coated PDMS substrates at room temperature for 12 h and then at 14°C for 24–48 h. Aplysia cells exhibited highly polarized outgrowth exhibiting long straight neurites. Experiments were conducted with cells from multiple animals (n > 19) and multiple vesicles (n > 200) were tracked for each cell.

Cell stretching

Neurons were stretched using a system developed for high-resolution live-imaging of cells under applied mechanical strain17. The system applied a static deformation to a stretchable polydimethylsiloxane (PDMS) cell culture substrate. In this study, cells were stretched (20%) or compressed (8%) for 40 min and then the deformation was removed. All time points prior to t = 0 min are internal controls. The substrate deformation was characterized experimentally by digital image correlation and computationally by the finite element method. It was found that the mechanical strain of the cell culture surface was uniform over greater than 95% of the surface area. The details of the stretching system have been previously published17.

Microscopy and image analysis

All images were collected on an Olympus IX81 using a (1.15 NA) water immersion objective lens (Olympus America, Center Valley, PA, USA). An Andor Neo sCMOS camera cooled to −30°C was used to record images (Andor Technology, Belfast, UK). All imaging parameters (e.g., light intensity, exposure time, gain, etc.) were kept constant during all experiments. Differential interference contrast (DIC) image sequences of neurons were captured at a rate of 200 frames per second. Videos were captured approximately every 5 min (n > 20 videos per cell). Image stack alignment to remove drift was completed with a subpixel registration algorithm39. Large dense core vesicle motion was tracked using an algorithm for precise particle tracking by polynomial fitting with Gaussian weight40 in MATLAB (The MathWorks, Natick, MA, USA). Vesicle radius is estimated via inflection points in the image intensity profile40. All computations, statistical analysis and plots were generated in MATLAB.

Temporal mean squared displacement analysis

To discriminate between active and passive motion, vesicle dynamics were analyzed using a temporal Mean Squared Displacement (tMSD) algorithm to extract the local behavior of the vesicle as a function of time6. The algorithm estimates the local behavior for time, t, by calculating the tMSD of a rolling window centered about the time of interest,

where indicates an average over timescale τ, r(t) is the position vector as a function of time, t′ is the time in the rolling window, τ is the timescale and τmax is the width of the rolling window (τmax = 500 ms). The tMSD is then fitted to a power law of the form, tMSD(τ) = Cτα on the interval 100–160 ms and the power law scaling, α(t), can be extracted as a function of time to indicate the type of diffusion the vesicle is undergoing (α < 1, subdiffusive; α = 1, Brownian; α > 1, superdiffusive). It should be noted that MSD analyses can be highly sensitive to noise and should be interpreted carefully41,42. Previously it has been shown in Aplysia neurons that α ≥ 1.4 is indicative of active motion driven via molecular motors and α < 1.4 is considered passive motion6. By convention, positive values indicate direction forward towards the neurite terminal (anterograde) and negative values are rearward (retrograde) towards the cell body. This method was used to determine if vesicles were undergoing active or passive motion as used throughout the study.