Introduction

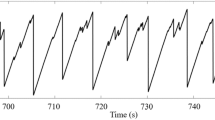
In this study, we analyze and model slowly-compressed pillars of bulk metallic glasses (BMGs)1,2,3,4,5,6,7,8 (Figure 1). The pillar deformation proceeds via slips, observable through acoustic-emission measurements5 or steps (serrations) in the stress-strain curves (Figure 2). Here we present a quantitative model and theory for the serration statistics in BMGs, which is critical for the understanding of the deformation behavior of BMGs. We compare our experimental results on BMGs with the predictions of our model, which has previously shown good agreement in describing the slip statistics of nano- and micro-crystals9,10,11. Furthermore, scaling collapses of the serration distributions at lower stresses predict the critical stress with roughly 5% accuracy. BMGs are non-crystalline amorphous alloys whose microstructures have no periodic long-range order1,2,3,4,5,6,7,8. In monotonic-compression tests, BMGs deform by the intermittent nucleation, propagation and subsequent arrest of shear bands in highly-localized regions of large compressive stresses12 (see the Supplementary Material). At a specific temperature and strain rate, a serrated plastic flow is usually observed in the compressive stress-strain curve after the yield point, marked by almost-periodically-recurring sudden stress drops with smaller stress drops during the loading intervals in-between. Cumulated shear bands can be as large as the system itself, or two to three orders of magnitudes smaller13. The slip sizes are broadly distributed14.

Figure 1
figure 1

(a) lateral surface of a fractured BMG sample, Zr64.13Cu15.75Ni10.12Al10, after compression at a strain rate of 5 × 10−5 s−1 and (b) magnified region indicated by a rectangle in (a) showing the interaction of multiple shear bands.

Full size image
Figure 2
figure 2

Compression stress-time profiles of Zr64.13Cu15.75Ni10.12Al10 ingots (by atomic percent)13,14.

Cylindrical samples, 2 mm in diameter and 4 mm in length, have been compressed along their 4-mm axis at fixed strain rates and at room temperature, 298 K. Insets show sudden drops in the applied stress, as the ingots are compressed at various constant strain rates. These stress drops indicate the occurrence of slip avalanches in the material.

Full size image

Our model9,10,11 predicts a power-law distribution of slip sizes multiplied with an exponentially-decaying cutoff function. The cutoff depends on experimentally-tunable parameters, such as strain rate or stress. The model is a mean-field model with no explicit spatial dependence. Thus, it predicts that the long length-scale behavior of the slip statistics should be universal and independent of microscopic structural details10. In particular, it predicts that the statistics of the slip avalanches in slowly-compressed BMGs have the same scaling behavior as those observed for slowly-compressed crystalline materials. In the following, we test this hypothesis. We first describe the model and then show the experimental results and their comparison to the model predictions.

The model10 assumes that typical materials have weak spots and that a slowly-increasing shear stress or a slow shear rate triggers weak spots to slip. Each weak spot is stuck until the local stress exceeds a random local failure stress. It then slips, thereby relaxing the local stress to a local (random) arrest stress. In crystals, the weak spots may be the location of dislocations and their slips correspond to dislocation slips. In BMGs, weak spots may be the locations of shear transformation zones (STZs), shear bands, liquid-like sites, or other relatively weak regions in the material12,15,16,17,18.

Weak spots are elastically coupled, so that a slipping weak spot can trigger other weak spots to slip, creating a slip avalanche. At the slowest (“adiabatic”) driving rate, a slip avalanche finishes before the next one is started. Slip avalanches are detected as steps in strain (for slowly-increasing stress-boundary conditions) or as stress drops (for fixed strain-rate-boundary conditions). The elastic interaction between the weak spots is sufficiently long-ranged so that mean-field theory (MFT), which assumes infinite range interactions, correctly predicts the scaling behavior of the slip statistics on long-length scales10. The MFT predictions agree with the slip statistics of slowly-compressed nanocrystals9. Here we study whether MFT can also predict the slip statistics in BMGs.

The MFT model predicts many statistical distributions and quantities, such as the probability distribution of slip sizes and the power spectra of the acoustic emission10 and their dependence on experimentally-tunable parameters, such as the applied strain rate and the stress.

For a low imposed strain rate, Ω and near-failure stresses, the MFT predicts that the probability-distribution function (PDF) of the magnitudes, S, of the stress-drop avalanches, scales in the steady state, where the time-averaged stress is constant, as11

This scaling form is predicted to be universal, i.e., independent of the microscopic details, with κ = 1.5. The exponentially-decaying cutoff is given by the universal scaling function, D′(SΩλ). It reflects that the maximum observed slip size, Smax, depends on the strain rate as Smax ~ Ω−λ. In MFT, the universal exponent is λ = 2 in the steady state.

The corresponding complementary cumulative distribution function (CCDF), C(S,Ω), which gives the probability of observing an avalanche of size greater than S, is useful for systems with low numbers of avalanches:

Here, C′(SΩλ) is another universal scaling function, λ(κ − 1) = 1 in MFT10,11 in the steady state and u ≡ SΩλ.

Likewise, for the lowest (“adiabatic”) strain rate, the distribution of stress-drop avalanches is predicted to follow a modified power law as a function of applied stress9,10. For f ≡ (1 − τ/τC), where τ is the applied stress and τC is the critical (failure) stress, the model predicts9,10:

where D″ is a universal scaling function and σ = 0.5 in MFT. The corresponding CCDF scales as9:

Again C″(x) is a universal scaling function9. The corresponding distributions were extracted from the experiments for slowly-compressed ingots of BMGs (see the Methods Section) and compared to the model predictions.

Widom scaling collapses19 of the experimental stress-drop size distributions yield the critical exponents, κ and λ, for the strain-rate-varied distributions and κ and 1/σ for the stress-binned distributions. In Figures 3 and 4, we plot C(S,Ω)Ω−λ(κ−1) versus SΩλ for the strain-rate-varied distributions and C(S,f)f−(κ−1)/σ versus Sf1/σ for the stress-binned distributions, respectively. The critical exponents (τ, λ, κ and σ) and τC are tuned until the curves lie on top of each other, thereby yielding the correct values of these critical exponents and τC. The collapses themselves describe the scaling functions, C′(SΩλ) and C″(Sf1/σ). Error bars for the exponents indicate the range of exponents that give approximately the same quality collapse.

Figure 3
figure 3

Complementary cumulative distribution functions (CCDFs), or survival functions, of stress drops for samples of Zr64.13Cu15.75Ni10.12Al10, 2 mm in diameter and 4 mm in length, compressed at various constant strain rates at 298 K.

Larger stress drops occur more frequently in samples that are strained more slowly, which agrees with the model's prediction19. The proposed model predicts a scaling form for the stress-drop probability-distribution functions (PDFs), which scale as S−κ times a universal scaling function dependent on the quantity, SΩλ, of Equation (1) in the main text. Appropriately integrating the predicted form of the PDFs, the CCDFs also show the functional dependence on SΩλ and the power-law dependence in S can be recast by a change of variables to a power-law dependence in Ω. The inset shows the CCDFs and stress-drop sizes rescaled by appropriate Ω-dependent scaling expressions, which effectively reveals the scaling function, C′(x), of Equation (2) in the main text. This scaling “collapse” was quantitatively verified for the exponent values of κ = 1.42 ± 0.20 and λ = 0.22 ± 0.02. With these exponents and the function, C′(x), shown in the inset, we can predict the serration statistics at other strain rates, see Equation (2).

Full size image
Figure 4
figure 4

CCDFs of stress drops in the most slowly-compressed sample (5 × 10−5 s−1) of Zr64.13Cu15.75Ni10.12Al10 at various average applied stresses.

Stress drops above the threshold of instrument-noise fluctuations (10 MPa) only set in around 92.0% of the maximum applied stress. Thus, small windows of stresses were examined: 94.0–96.0% (green dotted line), 96.0–97.0% (purple dashed line) and 97.0–97.6% (black solid line), with the weighted average stress values given in the figure legend. The stress-binned stress-drop PDFs are hypothesized to scale as a power-law dependence of S−κ multiplied by a scaling function dependent on S(1 − τ/τC)1/σ, see Equation (3) in the main text, which expresses the distance from criticality19. Because the bins of stresses are small, τ is taken to be the average applied stress within each bin. The resulting scaling collapse (inset) was quantitatively verified for the exponent values of κ = 1.4 ± 0.28, 1/σ = 1.85 ± 0.20 and τC/τMax = 1.05 ± 0.01. With these values and the collapse function, , shown in the inset, we can predict the slip statistics at other stresses, see Equation (4).

Full size image

Results

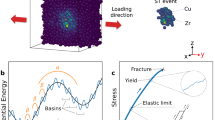
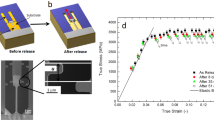
The morphology of a lateral surface after compressive fracture is described in Figure 1(a). Multiple primary shear bands can be found, denoted by the short white arrows and their slip direction is indicated by the long white arrow. With a closer look at the adjacent region of the fracture plane, which is marked by a rectangular in Figure 1(a), secondary shear bands can be located by the short white arrows in Figure 1(b). Furthermore, intensive interactions of shear bands appear in the lower-right part of the figure. The shear-band initiation, propagation and arrest, including the interaction between different shear bands, are expected to contribute to the serration events and these processes are closely related to the characteristics in deformation, such as the stress drop in the stress-strain curve.

The complementary cumulative distribution functions (CCDFs) of stress-drop magnitudes were extracted from the stress-time curves shown in Figure 2. First, CCDFs are constructed, taking stress drops from the entirety of each sample's stress-time curve. The CCDFs for three different strain rates are shown in the main body of Figure 3. The axes were rescaled by changing κ and λ until the distributions lie on top of each other9. For this collapse, it was found that κ = 1.42 ± 0.20 and λ = 0.22 ± 0.02. The collapse function in Figure 3 is the scaling function, C′(x), of Equation (2). Plugging this information into Equation (2) then predicts the scaling behavior of the slip-avalanche-size distribution for other strain rates as well. Note that for the higher strain rates, the samples break before they reach the steady state – Figure 2 shows that the stress versus time plots have no flat region for strain rates of 2 × 10−4 and 1 × 10−3 s−1.

The second collapse, shown in Figure 4, was performed on the most slowly-strained sample using CCDFs from stress bins near the critical failure stress. Nearly all of the stress drops occurred above 92.0% of the highest average stress achieved in the sample. Three partitions of average stresses were chosen – 94.0–96.0%, 96.0–97.0% and 97.0–97.6%, where the percentages indicate the percents of the maximum stress on the sample, 1,980 MPa. Avalanches were not sampled from higher than 97.6% of the maximum stress, because near the critical stress, the avalanche sizes are cut off by the finite system size, i.e., the avalanches “feel” the boundaries of the sample. In this region, finite-size corrections to the infinite system predictions of the theoretical model become non-negligible19. Therefore, it is preferable to keep the stress bins close, but not too close to the critical stress.

The second collapse yielded exponents of κ = 1.40 ± 0.28, 1/σ = 1.85 ± 0.20 and a relative critical stress ratio of τC/τMax = 1.05 ± 0.01. The error bars reflect statistical fluctuations resulting from the finite number of avalanches per sample. The parameter, τC/τMax, indicates the critical stress as a fraction of the maximum achieved stress, τMax = 1,980 MPa. The fitted critical stress, τC and the measured maximum applied stress, τMax, are slightly different in that the critical stress is the applied stress at which an infinite system is (by extrapolation) expected to yield in an infinitely-large avalanche. However, in a finite sample, one finds a sample-spanning avalanche at the maximum stress, which is below the critical stress.

The collapse function in the inset of Figure 4 is the scaling function, C″(x), of Equation (4). Plugging the extracted exponents, κ and 1/σ, the critical stress, τC and the scaling function, C″(x), into Equation (4) then predicts the scaling behavior of the slip-avalanche-size distribution for other stress windows as well.

Discussion

  1. 1

    We first compare the results on BMGs or amorphous materials to model predictions and crystal plasticity. The values of 1.42 ± 0.20 and 1.40 ± 0.28 for the magnitude scaling exponent, κ, in Figures 3 and 4, respectively, agree, within error bars, with the model prediction of κ = 3/210 using the mean-field theory. Within error bars, the values of 1.85 ± 0.20 for the exponent, 1/σ, in Figure 4, also agrees with the MFT prediction of 1/σ = 2. As expected, the experimental exponent, λ = 0.22, deviates from the value that the MFT predicts for the steady state, because at the higher shear rates, the samples do not reach the steady state. 234, 181 and 189 avalanches were collected for the samples at strain rates of 5 × 10−5, 2 × 10−4 and 1 × 10−3s−1, respectively.

    The stress-binned data contained 38, 28 and 26 avalanches in the bins with the average avalanche stresses at 95.2%, 96.5% and 97.3% of the maximum stress bins, respectively, in Figure 4. Stress bins were chosen to be small, because the BMG samples did not exhibit the avalanche behavior until about 92.0% of the maximum stress was achieved, originating from BMGs' high strength but limited ductility20,21. As explained above, finite-size effects affect the distribution of avalanches close to the critical fracture stress. Thus, stress bins must be kept a few percents below the maximum stress9. Note that the stress-binned data collapsed in the same way, with the same exponents, as stress-binned data on slowly-compressed nanocrystals9, illustrating the similar slip statistics of crystals and amorphous materials.

  2. 2

    Our MFT model assumes the presence of elastically-coupled weak spots. This assumption applies to BMGs for the following reasons. Recent studies reveal that structural heterogeneities exist in BMGs, which are mainly composed of solid-like (densely-packed) sites and liquid-like (anelastic) sites or so-called weak spots22,23,24,25. Using the amplitude-modulation dynamic atomic force microscopy (AM-AFM), one can easily find two types of sites from the local energy-dissipation map24,25. It should be pointed out that the correlation length of the heterogeneity equals ~ 2 nm, which is in good agreement with the size of STZs24,26,27. Furthermore, STZ dynamic simulations, based on the kinetic Monte Carlo method, have been performed to study the interaction between STZs during deformation in BMGs28. The results clearly show that at low stress levels, these STZs will behave separately, which corresponds to the elastic-deformation mode. When the stress exceeds a certain value, the activation of one STZ will induce the subsequent STZ activation in its immediate neighborhood, i.e., the slip of one weak spot triggers other weak spots to slip. These experimental and simulation results strongly support our model assumptions.

  3. 3

    The observed scaling behavior and the scaling collapse in the inset of Figure 3 reflect the tuned criticality. Ren et al.29 find that the elastic-energy density released in avalanche-slip events of BMGs follows a power-law distribution for a high strain rate (2.5 × 10−2 s−1), which they interpret as a signature of self-organized criticality (SOC). However, both their and our avalanche-size distributions reflect distinct strain-rate dependence. As shown in Figure 3, we observe avalanche-size distributions whose exponential cutoff moves to larger sizes with decreasing strain rate. The data of Ren et al.29 also show evidence of broader distributions (larger average stress-drop sizes) with decreasing strain rates, which may signify scaling with respect to strain rate. In other words, the strain rate here is a tuning parameter of the tuned critical point of BMGs9,19. Tuned criticality is fundamentally different from SOC, which always exhibits pure power-law scaling, without the need for parameter tuning to a critical point30. In contrast, the plastic flow in BMGs exhibits tuned criticality with a critical point at low strain rates and at near-failure stresses, similar to crystals. For both crystals9 and BMGs, the tuning parameters (strain rate and/or stress) must, thus, be tuned to their critical values in order to observe the power-law scaling behavior9,19.

Conclusions

In conclusion, we have presented new analysis and modeling of the dependence of avalanche statistics in BMGs on the applied strain rate and the stress. We obtained the first scaling collapse of the slip-avalanche statistics in BMGs. We have shown that the distribution of avalanche sizes varies with strain rate and applied stress, which indicates that both the strain rate and the applied stress are critical tuning parameters. Because we observe that the criticality is tuned, we conclude that the avalanche distributions reflect an ordinary (tuned) critical point rather than self-organized criticality in amorphous solid deformation.

A mean-field theoretical approach predicts the experimentally-achieved values for the critical scaling exponents. The strain-rate scaling exponent, λ, differs from the mean-field prediction for the steady state because at the higher strain rates, the samples are not in the steady state. Most importantly, we find that the critical exponents, κ and σ and the scaling forms are consistent within error bars with the predictions of our MFT. The critical exponents, κ and σ, also agree within error bars with recent experiments on nanocrystal plasticity9. Note that the exponent, λ, is yet to be determined for crystal plasticity. The present result suggests that the model's predictions and interpretation of serrations as slip avalanches of weak spots apply to both crystals and amorphous materials, irrespective of the microscopic details and structures. This observation implies that the same evaluation methods (using the slip-avalanche statistics and acoustic emission below the failure stress) can be employed to predict quantities, such as the critical stress, in both crystalline and BMG materials. Moreover, from the slip-size distributions at the lower strain rates, or at lower stresses, we can predict the serration statistics at higher strain rates or at higher stresses, respectively (see Figures 3 and 4, respectively).

Methods

Ingots of an amorphous Zr64.13Cu15.75Ni10.12Al10 (nominal atomic percents) BMG were prepared by arc-melting the alloy mixture of Zr, Cu, Ni and Al with purity higher than 99.9 weight percent in a Ti-gettered high-purity argon atmosphere. The melting and solicitation processes are repeated at least five times to achieve chemical homogeneity. Then the melted mixture is suction cast into a water-cooled copper mold to form a cylindrical cast rod, 60 mm in length and 2 mm in diameter13,14. The cast rods were then cut into cylindrical bars with 4 mm in length. The two compression faces of each bar were then carefully polished to be parallel to each other. The sample was uniaxially compressed at 298 K (room temperature) using a computer-controlled MTS 809 materials testing machine at a constant strain rate. Three strain rates, 5 × 10−5 s−1, 2 × 10−4 s−1 and 1 × 10−3 s−1 were employed in the compression experiments, with a data-acquisition rate of 33 Hz. Figure 1 shows images taken by scanning electron microscopy of the lateral surfaces of one of the compressively-fractured samples at a strain rate of 5 × 10−5 s−1. The fractograph clearly indicates the multiple shear bands along which the sample deformed.

The slowest strain rate, closest to the theoretical adiabatic limit, was selected and examined at different values of applied stresses to determine the stress dependence of the distribution of stress-drop avalanches. The sample compressed at 5 × 10−5 s−1 exhibits many avalanche events at stresses above 1,800 MPa, which is 92.0% of the maximum attained stress for this sample. The stress-drop avalanches were extracted for values of average-stress intervals of 94.0–96.0%, 96.0–97.0% and 97.0–97.6%.

The complementary cumulative distribution function (CCDF) of stress drops as a function of their magnitudes is constructed numerically for each different strain rate9. CCDFs are also constructed for each stress bin of the adiabatically-compressed sample.