Abstract
Microsystems become part of everyday life but their application is restricted by lack of strong and fast motors (actuators) converting energy into motion. For example, widespread internal combustion engines cannot be scaled down because combustion reactions are quenched in a small space. Here we present an actuator with the dimensions 100 × 100 × 5 μm3 that is using internal combustion of hydrogen and oxygen as part of its working cycle. Water electrolysis driven by short voltage pulses creates an extra pressure of 0.5–4 bar for a time of 100–400 μs in a chamber closed by a flexible membrane. When the pulses are switched off this pressure is released even faster allowing production of mechanical work in short cycles. We provide arguments that this unexpectedly fast pressure decrease is due to spontaneous combustion of the gases in the chamber. This actuator is the first step to truly microscopic combustion engines.
Similar content being viewed by others
Introduction
The last decennium has witnessed an impressive trend to miniaturize systems of virtually any kind. This trend has many reasons: small systems are often cheaper to produce, they can have properties large systems have not and they may facilitate use of large systems (cars, for example). An important and generic component in microsystems is the actuator. It plays role of a motor transforming electricity or other kind of energy into mechanical power. In contrast with large scale systems, where effective engines are available (internal combustion or electromagnetic motors), microsystems suffer from lack of strong and fast actuators1,2. Small electromagnetic motors cannot generate forces of useful magnitude but internal combustion engines just do not exist at the microscale.
The existing microcombusters3 cannot be a part of microsystems since they have only one dimension in the range of submillimeters. Microengines using gas combustion perform poorly due to increased heat losses via the volume boundary4,5 when the volume decreases. However, recently we observed that the reaction between H2 and O2 gases can be ignited spontaneously in stoichiometric nanobubbles smaller than 200 nm overcoming this restriction in some way6,7. The mechanism is still not clear, but it is expected that both high Laplace pressure and fast dynamics are important6. It is not obvious that the reaction in nanobubbles and performance of the microscopic actuator are related. Nevertheless, we speculate that the gas combustion in the chamber happens via combustion in transitional nanobubbles. Nanobubbles already demonstrated counterintuitive properties such as unexpectedly long life time of the surface nanobubbles (see8 for a review). Mechanism of this stability is still debated9,10,11,12 after more than 10 years of active discussion.
Existing microactuators are using mostly two types of forces1,2,13,14: electrostatic forces (weak) and those generated by thermal expansion (slow). Small electromagnetic motors cannot generate forces of useful magnitude but fast and strong piezoelectric elements are not compatible with microtechnology and need a high voltage for actuation. Some progress was achieved with the use of electroactive polymers15,16,17 but they are not suitable for many applications in microsystems. Electrochemical actuation was also discussed in many papers18,19,20,21,22,23,24 but it is notoriously slow. One can produce a large amount of gas in a short time but it is impossible to get rid of this gas also fast. In this paper we present an actuator that uses alternating polarity (AP) short-time electrolysis6,7 to produce H2 and O2 gases but termination of the gases happens very fast due to spontaneous combustion.
Results
Fabrication and characterization
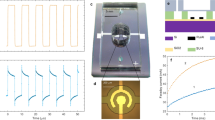
The actuators were fabricated on Si wafers covered with a layer of silicon rich nitride (SiRN) (thickness 530 nm) containing deposited Pt electrodes of different designs. This layer played the role of the actuator membrane. The membrane was made free by etching the wafer from the back side. The chamber and filling channels were isotropically etched in borofloat wafers. The glass and Si wafers were anodically bonded as shown in Fig. 1. A polysilicon thermal sensor designed for four-probe measurements was fabricated underneath the electrodes (see details in Supplementary). The bonded wafers were diced into separate chips with the size 2 × 1 cm2. The actuator chamber with the nominal dimensions 100 × 100 × 5 μm3 was filled via the channel (cross section 10 × 5 μm2) with a solution of Na2SO4 in deionized water. In most cases the salt concentration was around 1 M. The inlet and outlet openings were sealed with a foil, the chip was glued to a printed circuit board (PCB) with an opening in the middle to get access to the membrane from the back side. For one chip without the covering glass we calibrated the membrane deflection d in its center versus applied external pressure ΔP. It was found that ΔP = Ad + Bd3 where A = 2.03 bar/μm and B = 0.27 bar/μm3. This relation can be used to estimate the pressure in the chamber if d is known.
Design of the chip.
(a), A silicon wafer with a SiRN layer on top is bonded with a structured glass wafer. (b), Optical image of the chamber in the device before filling. The membrane (highlighted with green light from the bottom) is not completely etched, but normally it coincides with the size of the chamber. Under the central electrodes a thermal sensor (polysilicon) is visible. (c), General design of the chip: in/outlets, long channels and six contact pads (2 for the electrodes and 4 for the sensor). (d), Completely functioning device glued to a PCB, sealed and wire bonded.
Short square voltage pulses were applied to the electrodes. The response of the system was observed with a homemade stroboscope25 and with a vibrometer (Polytec MSA-400). In the latter case it was possible to observe the process from the top (via glass) or from the bottom focusing the laser beam (λ = 633 nm) with a diameter of 1.5 μm on the membrane. First, we measured the membrane deflection due to applied voltage pulses from the back side. For this configuration the change of the refractive index of the liquid due to different reasons (dissolved gas, heating, pressure change) does not influence the signal of the interferometer. Bubbles with the radius r > λ/2π appearing in the chamber can scatter the light because the membrane is transparent. To eliminate their effect on the signal we focused the laser beam on the opaque electrode. With these precautions we can be sure that the measured signal corresponds to the velocity of the membrane about 10 μm off its center (see Supplementary Fig. S1).
Electrochemical cell
To achieve a significant actuation stroke in a short time we have to produce a large amount of gas. For this a large current through the chamber is needed. An electrochemical cell supports a large current in the ohmic regime when the current I and voltage U are related as26I ≈ (U − E0)/R. Here E0 is the water dissociation potential and R is the resistance of the cell. Both of the parameters are defined by the cell and it was already noted7 that for microsystems these parameters are considerably larger than for macrocells. For example, the I − U curve for one of our sample (see Supplementary Fig. S2) corresponds to E0 = 2.8 V and R = 3.7 kΩ. Therefore, to run the actuation fast we need a larger voltage than usually used for electrolysis. In our experiments we used AP pulses with the amplitude U = 5–10 V.
The average current density for our chips is around 200 A cm−2. It results in a very high relative supersaturation S > 1000 nearby the electrode surface. When S is so large the bubbles nucleate homogeneously and exist in the form of nanobubbles during 100 μs or so7. For single polarity electrolysis the bubbles finally grow to a well visible microscopic size, but for AP electrolysis only small number of microbubbles is observed if the switching frequency is larger than 20 kHz (see6 and Supplementary Fig. S3). Some additional information and estimates are given in Supplementary Information. Let us note that for macroscopic electrolytic cells observed on a long-time scale27 the maximal current density is ~1 A cm−2 and maximal supersaturation is ~100.
Membrane deflection
For AP voltage pulses with the amplitude U = ±10 V repeated with the frequency f = 50 kHz (driving or switching frequency) during τ = 600 μs the signal and current are shown in Fig. 2. The signal consists of separate narrow lines of increasing amplitude correlated with the driving pulses. It is well visible in Fig. 2d where only five periods for both the signal and current are shown in the same plot. The signal in Fig. 2a integrated over time t is the deflection of the membrane d(t). It is shown in Fig. 2c. The deflection increases with time finally reaching a steady state while oscillations with the driving frequency f are superimposed on the smooth curve (see enlarged view in Fig. 2e). In its maximum the deflection becomes as high as d ≈ 1.4 μm that corresponds to the pressure increase in the chamber ΔP ≈ 3.6 bar.
Deflection of the actuator membrane measured from the back side.
The membrane is driven by AP voltage pulses U = ±10 V, f = 50 kHz and τ = 600 μs. (a), Velocity of the membrane (raw signal of the vibrometer). (b), Current flowing through the electrodes. (c), Deflection of the membrane (raw signal integrated over time). (d), Five last periods of the signal in (a) and the current in (b) are shown in the same plot. (e), Five last periods in the membrane deflection.
When the electrochemical process is switched off the pressure drops very fast (see Fig. 2c). This is our key observation that opens the way for a closed actuation cycle. A huge amount of gas disappears in 100 μs or so. The maximal deflection of the membrane corresponds to the apparent volume of gas ΔV = 0.7 × 104 μm3 at the pressure P ≈ 4.6 bar. As the pressure is reduced back to normal this gas has to fill 60% of the chamber but no gas is visible. The actual amount of gas is much larger. This is because most of the gas is densely packed in nanobubbles (see6,7 and estimates in Supplementary Information). Only small amount of gas can be dissolved in the chamber to saturate the liquid. Diffusion out of the chamber via the filling channels is negligible on this timescale. Moreover, the gas produced by the single polarity electrolysis, when hydrogen and oxygen are separated in space (appear near different electrodes), is well visible and exists on a longer timescale (see Supplementary Fig. S3). The only reasonable explanation of the observed fast pressure decrease is consumption of the gases in the overall reaction of water formation. We cannot separate elementary steps in this reaction but the process is not catalytic. In 600 μs the gases diffuse too far away from the electrodes (a few μm) to be consumed in surface reactions in 100 μs.
Discussion
Our interpretation of the physical events presented in Fig. 2 is the following. Stoichiometric nanobubbles that are formed nearby the electrode surface in phase with the electrical pulses6 are responsible for the sharp peaks in Fig. 2a and 2d. Previously we observed periodic reduction of gas concentration in the electrolyte above the electrodes6. Here we can see that in the closed chamber the process is accompanied also by the periodic variation of the pressure. This is an independent argument that the combustion reaction happens in the nanobubbles. The monotonic pressure increase in Fig. 2c is due to the gas existing as separate hydrogen and oxygen nanobubbles and dissolved molecules. The nanobubbles are formed homogeneously and very fast because the local supersaturations is high. For each period more gas is produced than consumed while a steady state is not reached. In the steady state a part of the produced gas disappears in correlation with the driving pulses (high frequency oscillation). The rest of gas gets into the reaction independently on the electrical pulses (randomly) by formation of stoichiometric nanobubbles in the solution. This random process is responsible for the fast decrease of the pressure after the switch off. The details of this interpretation can change, but the solid fact – the fast pressure decrease – has to be related to the reaction between H2 and O2.
Thermal effect
The deflection of the membrane demonstrates dependence on the driving frequency f as shown in Fig. 3a. The higher the frequency the smaller amount of gas escapes the reaction resulting in a smaller increase of pressure. For this reason the heat produced by the combustion reaction must increase with f. On the contrary, the Joule heating does not depend on f. This is a clear experimental signature to distinct between the two sources of heating. To see the thermal effect we observe variations of the electrolyte conductivity similar to that for any resistive sensor. We fit each current pulse (half of a period) with the function7I(t) = IF + I1 e−kt, where IF is the Faraday current and the second term (parameters I1 and k) describes surface charge-discharge processes28. Figure 3b shows the Faraday current as a function of time for different frequencies. The current increase with time demonstrates the effect of heating. Faster increase for higher frequencies shows that at least a part of the total heat is produced by the reaction. Observation of the heating became possible due to small thermal mass of the membrane.
Heating due to combustion of gases.
(a), Deflection of the membrane for different driving frequencies (U = ±9 V, τ = 350 μs). (b), The Faraday current as a function of time for the runs presented in (a) (one point per period). The inset shows the effective temperature (smoothed) in the chamber. Different colors correspond to the frequencies shown in (a).
To estimate an effective temperature in the chamber we measured (using METTLER TOLEDO SevenMulti) the conductivity of the bulk solution, σ = σ0(1 + αΔT), as a function of the temperature increase ΔT to find σ0 = 15 Ω−1m−1 at T = 20°C and α = 0.024 K−1. Independently α = 0.024 ± 0.001 K−1 was determined from our samples using external heating. The temperature dependence of the Faraday current was used to extract information on the effective temperature (see inset in Fig. 3b). The temperature determined in this way is closer to the maximal temperature than to the average one because the most significant contribution to the current comes from the hottest regions around the electrodes. Our built-in thermal sensors were not fast enough to measure the temperature change on the time scale 100 μs presumably due to parasitic electrical effects.
Even for very high supersaturation the homogeneous nucleation is still an activation process. Heating increases the nucleation rate including the bubbles containing only H2 or O2 gases. Because more unreacted gas appears in the chamber the pressure has to increase faster. This effect is responsible for faster than linear increase of d(t) in Figure 3a. A similar behavior has to be observed when the external temperature increases. To see this effect one chip was glued to a flat resistive heater and calibrated with a thermocouple. This configuration was observed from the top. The vibrometer results were equivalent to that observed from the bottom except of occasional scattering on microbubbles appearing more often at low frequencies or high currents. The results shown in Fig. 4a demonstrate significant dependence of the deflection on temperature. Scattering on microbubbles is visible as some irregularity for the curve at T = 30°C.
Influence of heating on the actuator performance.
(a), Membrane deflection for different external temperatures (U = ±10 V, f = 100 kHz, τ = 400 μs, low current sample). (b), Membrane deflection for two successive series of pulses 100 μs long each separated by different delay times. For the curves 1, 2, 3 and 4 the delay is 100, 200, 400, 600 μs, respectively.
Actuation frequency
The dynamics of cooling was observed by applying two series of driving pulses separated by a delay time. The membrane deflection is shown in Figure 4b. The first series of pulses 100 μs long heats up the system. The second series is started when the temperature nearby the electrodes is augmented resulting in a larger deflection than the first one. When the delay between the series of pulses increases the effect fades away. The same experiment demonstrates how fast the membrane can be actuated using series of pulses separated in time (see also Supplementary Fig. S4). From our data it follows that cyclic operation with an actuation frequency of F = 5 kHz is feasible and at this frequency the actuator is able to deliver the overpressure on the level of 1 bar. Small increase in the external temperature can increase both the actuation frequency and the developed force. The maximal stoke can be reached for the minimal driving frequency around f = 20 kHz, however, for small f degradation of electrodes is observed6 and the optimal driving frequency is a matter of durability and material choice. Of course, the actuation with the driving frequency F = f ~ 100 kHz is also possible but with a smaller amplitude (pressure).
In conclusion, the results reported in this paper not only demonstrate a fast and strong actuator that can be applied in microfluidics, micro/nano positioning, or in compact sound/ultrasound emitters. More importantly, they demonstrate feasibility of combustion reactions in microscopic volumes. This is a fundamental statement that opens up new possibilities to power micro and mini systems.
References
Abhari, F., Jaafar, H. & Yunus, N. A. M. A comprehensive study of micropumps technologies. Int. J. Electrochem. Sci. 7, 9765–9780 (2012).
Ashraf, M. W., Tayyaba, S. & Afzulpurkar, N. Micro electromechanical systems (MEMS) based microfluidic devices for biomedical applications. Int. J. Mol. Sci. 12, 3648–3704 (2011).
Maruta, K. Micro and mesoscale combustion. Proc. Combust. Inst. 33, 125–150 (2011).
Veser, G. Experimental and theoretical investigation of H2 oxidation in a high-temperature catalytic microreactor. Chem. Eng. Sci. 56, 1265–1273 (2001).
Fernandez-Pello, A. C. Micro-power generation using combustion: issues and approaches. Proc. Combust. Inst. 29, 883–899 (2002).
Svetovoy, V. B., Sanders, R. G. P., Lammerink, T. S. J. & Elwenspoek, M. C. Combustion of hydrogen-oxygen mixture in electrochemically generated nanobubbles. Phys. Rev. E 84, 035302(R) (2011).
Svetovoy, V. B., Sanders, R. G. P. & Elwenspoek, M. C. Transient nanobubbles in short-time electrolysis. J. Phys.: Cond. Matter. 25, 184002 (2013).
Seddon, J. R. T., Lohse, D., Ducker, W. A. & Craig, V. S. J. A deliberation on nanobubbles at surfaces and in bulk. Chem. Phys. Chem. 13, 2179–2187 (2012).
Brenner, M. P. & Lohse, D. Dynamic equilibrium mechanism for surface nanobubble stabilization. Phys. Rev. Lett. 101, 214505 (2008).
Ducker, W. A. Contact angle and stability of interfacial nanobubbles. Langmuir 25, 8907–8910 (2009).
Seddon, J. R. T., Zandvliet, H. J. W. & Lohse, D. Knudsen gas provides nanobubble stability. Phys. Rev. Lett. 107, 116101 (2011).
Weijs, J. H. & Lohse, D. Why surface nanobubbles live for hours. Phys. Rev. Lett. 110, 054501 (2013).
Weiss, L. Power production from phase change in MEMS and micro devices, a review. Int. J. Therm. Sci. 50, 639–647 (2011).
De Volder, M. & Reynaerts, D. Pneumatic and hydraulic microactuators: a review. J. Micromech. Microeng. 20, 043001 (2010).
Pelrine, R., Kornbluh, R., Pei, Q. & Joseph, J. High-speed electrically actuated elastomers with strain greater than 100%. Science 287, 836–839 (2000).
Brochu, P. & Pei, Q. B. Advances in dielectric elastomers for actuators and artificial muscles. Macromol. Rapid Commun. 31, 10–36 (2010).
Shian, S., Diebold, R. M. & Clarke, D. R. Tunable lenses using transparent dielectric elastomer actuators. Optics Express 21, 8669–8676 (2013).
Neagu, C. R., Gardeniers, J. G. E., Elwenspoek, M. C. & Kelly, J. J. An electrochemical microactuator: principle and first results. J. Microelectromechan. Syst. 5, 2–9 (1996).
Cameron, C. G. & Freund, M. S. Electrolytic actuators: alternative, high performance, material-based devices. Proc. Natl. Acad. Sci. USA 99, 7827–7831 (2002).
Hua, S. Z., Sachs, F., Yang, D. X. & Chopra, H. D. Microfluidic actuation using electrochemically generated bubbles. Anal. Chem. 74, 6392–6396 (2002).
Ateya, D. A., Shah, A. A. & Hua, S. Z. An electrochemically actuated micropump. Rev. Sci. Instrum. 75, 915–920 (2004).
Meng, D. D. & Kim, C. J. Micropumping of liquid by directional growth and selective venting of gas bubbles. Lab Chip 8, 958–968 (2008).
Kjeang, E., Djilali, N. & Sinton, D. Microfluidic fuel cells: a review. J. Power Sources 186, 353–369 (2009).
Li, P.-Y., Sheybani, R., Gutierrez, C. A., Kuo, J. T. W. & Meng, E. A parylene bellows electrochemical actuator. J. Microelectromechan. S. 19, 215–228 (2010).
Van den Broek, D. M. & Elwenspoek, M. Bubble nucleation in an explosive micro-bubble actuator. J. Micromech. Microeng. 18, 064003 (2008).
Shen, M., Bennett, N., Ding, Y. & Scott, K. A concise model for evaluating water electrolysis. Int. J. Hydrogen Energy 36, 14335–14341 (2011).
Vogt, H. & Balzer, R. J. The bubble coverage of gas-evolving electrodes in stagnant electrolytes. Electrochem. Acta 50, 2073 (2005).
Bard, A. J. & Faulkner, L. R. Electrochemical Methods (Wiley, New York, USA 1980).
Acknowledgements
Funding was provided by the Dutch Technology Foundation (STW). We thank D. Lohse for numerous discussions, J.W. Berenschot for discussion of fabrication issues and H. van Wolferen for technical assistance.
Author information
Authors and Affiliations
Contributions
V.B.S. performed experiments and analysis; R.G.P.S. contributed to measurements and development of the setup; K.M. contributed to the device fabrication; M.C.E. contributed to the analysis; both V.B.S. and M.C.E. contributed to the writing of the paper. All authors were involved in discussions.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplemental Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Svetovoy, V., Sanders, R., Ma, K. et al. New type of microengine using internal combustion of hydrogen and oxygen. Sci Rep 4, 4296 (2014). https://doi.org/10.1038/srep04296
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep04296
This article is cited by
-
A strong and fast millimeter-sized soft pneumatic actuator based on alternative pole water electrolysis
International Journal of Intelligent Robotics and Applications (2024)
-
Nanoreactors in action for a durable microactuator using spontaneous combustion of gases in nanobubbles
Scientific Reports (2022)
-
Highly energetic phenomena in water electrolysis
Scientific Reports (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.