Introduction

In 1935, Einstein, Podolsky and Rosen (EPR) questioned the completeness of quantum mechanics (QM) based on local realism1. Many efforts have been devoted to a deeper understanding of QM in the form of three types of quantum nonlocalities: quantum entanglement, EPR steering and Bell nonlocality2. Within the hierarchy of nonlocalities, the set of EPR steerable states is a subset of entangled states and a superset of Bell nonlocal states. Quantum entanglement and Bell nonlocality have attained flourishing developments since 1964. However, EPR steering is a newly emerged research topic and, to date, is far from being completely understood. Steering inequalities for EPR steering are the analog of Bell inequalities for Bell nonlocality. Their violations, predicted by quantum mechanics, reveal EPR steering. Such a violation rules out the existence of a local-hidden-state (LHS) model, the same way the violation of a Bell inequality rules out the existence of a local-hidden-variable (LHV) model. In comparison to the development of Bell nonlocality, the research on EPR steering is in its developing stages, even though Schrödinger discussed the concept in 19353. A reason for this is the absence of a rigorous formulation of the concept of EPR steering, which did not appear until the work of Wiseman, Jones and Doherty2 in 2007. Indeed, EPR steering answers a question of fundamental quantum physics as well as opens new possibilities for quantum communication, thus it has inspired some recent research in quantum information theory4.

For a pure entangled state shared by two separated observers Alice and Bob, Bob's qubit can be “steered” into different states although Alice has no access to the qubit. Schrödinger adopted the word steering to describe this type of nonlocality. This means that Alice has the ability to remotely prepare Bob's particle in different states by measuring her particle using different settings and here we use to denote the conditional state Bob gets if Alice measures her particle with measurement and obtains result a. While Bob suspects that Alice may send him some non-entangled particles and fabricate the results based her knowledge of LHS. If Bob's system admits a LHS model , where ρξ's are states that Bob does not know (but Alice knows) and is the probability of ρξ, then Alice could attempt to fabricate the results using her knowledge of ξ, in other words, , with . If Bob finds there is a LHS model which can describe his conditional states after he asks Alice to perform the measurement on her particle, then he is not convinced the existence of EPR steering.

Very recently many results have been achieved to show violations of steering inequalities both theoretically and experimentally, thus rendering LHS model untenable5,6,7,8,9,10,11. However, the existed steering inequalities in the literatures are far from well-developed and therefore it is not yet possible to observe EPR steering for some steerable mixed states12. Another elegant approach to explore the contradiction between QM and LHS model is the all-versus-nothing (AVN) proof of the existence of EPR steering. This can be considered as the steering analog of Greenberger-Horne-Zeilinger (GHZ) argument without inequalities for Bell nonlocality13. Currently such an AVN proof for EPR steering has been shown to be a strong condition to witness the steerability of a family of two-qubit (pure or mixed) entangled states and have the ability of detecting asymmetric steering12. This also offers an effective way to detect EPR steering for two qubits experimentally.

In this work, we investigate the test of EPR steering according to its AVN argument and demonstrate directly the contradiction between LHS model and QM. We show that by observing projective probabilities, the existence of steering can be verified by defining a probability bound imposed by LHS model. Our test is the first one proposed to detect EPR steering based on the AVN proof and it is suitable for all the two-qubit entangled states specified in Ref. 12, both pure and mixed. The possible implementation of our test is discussed by using non-Abelian Fibonacci anyons and trapped ions, but it is not limited to these systems. Our test is also applicable to many other physical systems, such as photons, atoms as well as superconductors, etc. In a system of non-Abelian Fibonacci anyons, each logical qubit is encoded into triplet of Fibonacci anyons and the corresponding operations are carried out by braiding the anyons. As braids are performed by taking an anyon either around another or not, which will not cause small errors from slight imprecisions in the way that anyons are moved. Therefore, the test is fault-tolerant to errors and offers high experimental precision. In an ion-trap experiment, present experimental achievements on high-fidelity state initialization, quantum gates and state readout make our scheme of detecting steering possibly testable.

Results

First let Alice and Bob share a pure entangled state |Ψ〉AB = cos θ|00〉AB + sin θ|11〉AB. In the steering scenario, Alice adopts the following settings: , where and denote Alice's projective measurements in -and -directions and a (with a = 0, 1) is measurement result. After Alice's measurements, Bob's conditional states become

where describes Bob's state after Alice performs measurement and obtains result a and |ψ〉B = cos θ|0〉B + sin θ|1〉B, |φ〉B = cos θ|0〉B − sin θ|1〉B. If there exists a LHS model can fake the results (1), i.e., there exists a suitable ensemble and a stochastic map satisfying , then Bob is not convinced that Alice can steer his conditional states. Otherwise the LHS model contradicts with QM.

According to the AVN proof12, the entangled state |Ψ〉AB cannot be described by any LHS model except θ = 0 or π/2. The incisive contradiction between QM and LHS model is due to different predicted projective probabilities as stated in the following. For QM, Bob obtains zero probabilities after he performs some appropriate projective measurements on his qubit

where |ψ⊥〉B = sin θ|0〉B − cos θ|1〉B and |φ⊥〉B = sin θ|0〉B + cos θ|1〉B are orthogonal to |ψ〉B and |φ〉B, respectively. However, for a LHS model, it predicts the corresponding probabilities as follows,

From the AVN proof12, we know that the state |Ψ〉AB possesses EPR steering if θ ≠ 0 or π/2 and this tells us there exists no LHS model of the state such that . When θ = 0 or π/2, the state is separable and hence it is possible to find a LHS model to describe it. Therefore, we know that the probabilities (3) cannot be zero simultaneously except θ = 0 or π/2.

In an ideal test for EPR steering, after Alice performs projective measurement on her qubit of the state |Ψ〉AB, Bob then measures the probabilities by projecting the states |0〉B, |1〉B, |ψ⊥〉B and |φ⊥〉B on his qubits. If he finds the four probabilities are all zero, then EPR steering is demonstrated. Nevertheless, in real experiments (Exp), measurement results are inevitably affected by experimental precision and errors. It is possible that the probabilities obtained experimentally may deviate from the theoretical values slightly, i.e., (here εi are small numbers caused by errors). We then investigate how close a LHS model could be to simulate Eq. (2). We have shown that for the state |Ψ〉AB the probabilities only if the state shared by Alice and Bob is not steerable, otherwise, some of cannot be zero. For the sake of simplicity, consider the inevitable errors εi = ε for all i, we can detect steerability if for some i. Therefore, the optimal LHS model for this experiment is the one making approach to as closely as possible for all i. We define

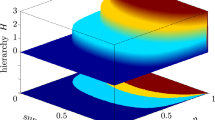
where Δ describes the bound of probabilities imposed by the optimal LHS model. In our test, EPR steering can be detected when Δ > ε. Fig. 1(a) shows the relation between parameter θ and Δ obtained numerically (see the Methods section). We find that Δ is of order 10−2 when θ is not closed to 0 or π/2. This implies that the EPR steering of state |Ψ〉AB can be revealed by the experiments with precision ε < 10−3. In Fig. 1(a), it is observed that Δ changes symmetrically with respect to θ and approaches to its maximal value when θ = π/4. This shows the more entangled the state is, the easier to detect EPR steering in the experiment.

Figure 1
figure 1

Numerical results of the bound Δ imposed by the optimal LHS model versus θ.

For (a) |Ψ〉AB and (b) ρAB.

Full size image

We next consider a two-qubit mixed state

Here and are two Bell states. The measurement settings of Alice are still and after Alice performs measurement and obtains result a, Bob's conditional states can be expressed as provided with a LHS model and a stochastic map . Similarly, for the state ρAB, Bob obtains quantum probabilities of measuring his qubit in the states |0〉B, |1〉B, |+〉B and |−〉B as

where and is Bob's conditional state after Alice performs projective measurement in -direction, etc. It has been proved that there does not exist any LHS model for ρAB with 12 such that probability equations in (6) can be satisfied simultaneously. If Bob observes experimentally these four probabilities , then EPR steering of the state is exhibited, or there exists no LHS model. Consider experimental imprecision and errors, we also investigate the condition to detect EPR steering of ρAB by plotting the variation of LHS bound Δ versus θ, see Fig. 1 (b). It can be found that for the experiments with precision ε < 10−3, the EPR steering of ρAB can be observed when θ is not close to π/4. It is worthy of pointing out that our test of EPR steering is not limited to the states |Ψ〉AB and ρAB, but also applicable to the family of two-qubit entangled states specified in Ref. 12, regardless of pure or mixed.

Discussions

Let us make some discussions on the possible realization of our test in physical systems. We first consider non-Abelian Fibonacci anyons which are shown to be the simplest non-Abelian quasiparticles for universal topological quantum computation14. Follow Freedman et al.'s work15, we encode logical qubits into triplets of anyons with total topological charge 1: |0〉L = |((·, ·)I, ·)τ〉 and |1〉L = |((·, ·)τ, ·)τ〉 (here L denotes “logical”). The so-called noncomputational state |NC〉 = |((·, ·)τ, ·)I〉 is the only state of three anyons that has total topological charge 0. Quantum operations can be constructed by using two elementary braiding operations R1, R2 acting on the Hilbert space of three Fibonacci anyons and their inverses16,17. The obtained quantum gates, together with the controlled-NOT gate obtained in Refs. 16,17,18 are useful in the construction of EPR steering test by preparing logical-qubit states and achieving required operations (see the Methods section). Several candidates for realizing non-Abelian anyons have been suggested in physical systems, such as fractional quantum Hall liquid19, rotating Bose-Einstein condensates20, as well as quantum spin systems21,22.

Another possible system to explore the realization of our test experimentally is trapped ion. Refs. 23,24,25 have reported experimental results of high-fidelity state preparation, quantum gate operations and state measurement for optical qubits stored in 40Ca+ held in a trap. State preparation is usually done by precisely manipulating the internal levels of ion utilizing laser pulses and the Blatt group realized state initialization with fidelity more than 99.8%24. By a Mølmer-Sørensen-type gate operation26,27, a Bell-type entangled state of ions with a fidelity of 99.3(1)% was realized in the same work24. The Blatt group also presented single-qubit gates with fidelity exceeding 99.9% in trapped ions23. As for state measurement capability in an ion-trap experiment, A. H. Myerson et al.25 achieved 99.991(1)% readout fidelity, sufficient for fault-tolerant quantum computation by measuring population of states using time-resolved photon counting. For the entangled state realized in Ref. 24, the probability bound is found to be Δ = 0.0732 and this means that the EPR steering of the entangled state can be verified experimentally with precision ε < 0.0732. The experimental achievements in the literatures23,24,25 tell us that our test of EPR steering based on the AVN proof is possibly realizable with current techniques in ion-trap experiments.

To summarize, we have presented a test to identify EPR steering based on the AVN argument by measuring projective probabilities. Our test is applicable to the family of two-qubit entangled states specified in Ref. 12 regardless of pure or mixed. We have provided the condition on experimental implementation of our scheme through expression (4) that EPR steering can be observed in the presence of experimental imprecision and errors. Our result is the first experimental test presented to detect EPR steering by resorting to the AVN proof and it can be implemented in systems such as non-Abelian anyons and trapped ions. The primary advantage of our test based on non-Abelian anyons is that it is fault-tolerant, or the logical quantum state used is robust against local perturbations. Specifically, it has been proven that these logical qubits might be robust to random perturbations28. Our test can also be realizable in ion-trap experiments based on current experimental techniques as recent progress in trapped ion offers high-fidelity state preparation, quantum gate operations and state measurement for optical qubits stored in it. Let us point out that the realization of our test is not limited to the two systems but also applicable to many other physical systems like photons, atoms and superconductors, etc. We expect further investigations in this direction, both theoretically and experimentally.

Methods

To find the optimal LHS model

We here present a theorem which is used to find the optimal LHS model for a given two-qubit state. Theorem – For any given two-qubit state ρABin a N -setting protocol, if there is a LHS model for the state, then there is a LHS model with the number of hidden states no larger than 2N. The proof of the Theorem needs two lemmas associated with the concept of deterministic LHS (dLHS) model which is a LHS satisfying , , ξ, a. We also briefly restate the notations to be used, is the conditional states of Bob after Alice measures and gets result a ∈ {0, 1}, the tilde here denotes this state is unnormalized and its norm is , the probability associated with the output a.

Lemma 1

For any given two-qubit state ρAB, if there is a LHS model for ρAB then there is a dLHS model for ρAB.

In a general N-setting protocol, we have . Suppose ρAB has a LHS description thus there is an ensemble and an associated probability fulfilling . We note that . Now if , , then it is a dLHS model. We next check each ξ to see whether . For any ξ with , we keep these terms unchanged. For , we decompose this term into 2N separate terms as follows. First we define a new term , where ai denote the measurement results of Ai (ai = 0, 1). It is not difficult to find that ma ranges from 1 to 2N depending on ai. We then do the decomposion by choosing

where is the hidden state and is its weight. By direct calculations it can be verified that . Eq. (9) shows the reconstructed stochastic maps are all deterministic. Thus by this way, we get a dLHS model that satisfies .

Lemma 2

For a dLHS model, can be rewritten as , where stands for the set of hidden states that contribute to indicating the corresponding . The equality holds if and only if the following equalities are fulfilled,

where and are the Bloch vectors of and ρξ respectively.

Let us look at the proof of the lemma. We have and , where 1 describes identity matrix. So the equality of gives . Thus we obtain Eq. (10).

We would like to point out that Eq. (10) is similar to the problem describing center of mass if we treat the probabilities and as masses, as well as Bloch vectors ( and ) as the position vectors of various masses. Lemma 2 shows that the task to find a dLHS model for a state with probability is equivalent to find a distribution of masses in the Bloch sphere with total mass and center of mass being located at . We show in the following that with the aid of Eq. (10), we can impose constraints on measurement settings to find a dLHS model. If we cannot find a dLHS model for ρAB, Lemma 1 shows that we can neither find a LHS model and this thus affirms the steerability of ρAB. For any given ρξ, we can always assign a N-length bit string constructed from considering . Next let us describe the LHS model by dividing hidden states {ρξ} into many subsets with each subset containing all of the ρξ that has the same N-length bit string. Thus in this way, each subset is unique, or not overlapping with others. We can take each of the subsets as one new hidden state by resorting to Lemma 2. We use the fact that hidden state can be treated as mass point so we can consider the centre of mass of each subset as the new state and the weight of the new state is the correspoinding total mass. It is not difficult to find that there are totally 2N such new states and thus the LHS model has only 2N hidden states. This ends our proof of the Theorem.

Therefore we conclude that the optimal LHS model contains an ensemble with four pure hidden states in the two-setting protocol and more hidden states make no improvement. The optimal LHS model is numerically obtained by minimizing function for a large n, where . In this approach, we utilize the knowledge of vector norm. First we have (Fn)1/n which is the ln-norm of vector . We know that l∞ -norm of a vector is just its maximum element and hence by definition Δ equals to the minimum of l∞-norm of the vector . So for a large enough n we can get a good approximation of Δ from minimizing (Fn)1/n with varied ρξ. In our calculations, we use n = 46 since we find numerically the improvement of Δ by choosing a number larger than 46 is negligibly small. As shown in Fig. 3 (a) and (b), we find the values of Δ by choosing θ = π/8, π/6 for |Ψ〉AB with different n (ranging from 20 to 120). It is clear that the values of Δ do not change substantially and the change is in the ten-thousandths place when n is greater than 45. The results show us that n = 46 is large enough to obtain a reasonable value of Δ. Apparemently we can choose other values of n as long as n > 45 and the choice will not affect the value of Δ much. We also plot the variation of Δ versus θ by choosing different n for |Ψ〉AB in Fig. 3 (c). Seen from Fig. 3 (c), the three curves corresponding to n = 46, n = 50, n = 100 respectively are almost overlapped. Hence we know that n = 46 is large enough to obtain a reasonable value of Δ.

Figure 3
figure 3

Variations of Δ for |Ψ〉AB versus n/θ.

(a) θ = π/8 and n ranges from 20 to 120, (b) θ = π/6 and n ranges from 20 to 120, as well as (c) n = 46, 50, 100 and θ ranges from 0 to π/2. From (a) and (b), we find that the variation of Δ is negligibly small when n > 45 since the variation is in the ten-thousandths place. From (c) it is clear that the three curves are almost overlapped and the results show that n = 46 is large enough to obtain a reasonable value of Δ.

Full size image

Approximation of quantum gates in non-Abelian Fibonacci anyons

Quantum operations can be constructed by using two elementary braiding operations R1, R2 acting on the Hilbert space of three Fibonacci anyons and their inverses16,17. In Fig. 2, we plot the braids that approximate the quantum gate

with U1 = Uπ/6 and U2 = U−π/3. Any other quantum gate Uθ can be obtained in a similar way. The approximations are obtained by performing brute force searches and the distance between two matrices ℳ and ℳ′ is defined as the square root of the largest eigenvalues of (ℳ−ℳ′)†(ℳ−ℳ′)16,17. The distances between the required operations and the gates resulting from actual braiding are about 5.7 × 10−5 for U1 and U2. In fact, these gates can be systematically improved to any required accuracy due to the Solovay-Kitaev theorem29. The above quantum gates, together with the controlled-NOT gate obtained in Refs. 16,17,18 are useful in the construction of EPR steering test by preparing logical-qubit states. We apply the operation Uθ (with θ ∈ (0, π/2)) on the logical qubit A of initial state and a controlled-NOT gate is followed on the two logical qubits, then we have the two-logical-qubit pure states . To prepare mixed state, we need an ancilla logical qubit C and initially assume that the logical qubits are in the state . We apply Hadamard gate on logical qubit A, Uθ on logical qubit C, then a controlled-NOT gate on logical qubits A and B and finally a controlled-NOT gate on logical qubits C and B, we then have . Look at the first two qubits only, we successfully have the state as in (5). All the operations involved in our scheme, such as and for Alice, and for Bob, can be carried out by braiding the Fibonacci anyons. For instance, the single-logical-qubit states and of Bob can be realized by using the action of U±θ on (up to a global phase).

Figure 2
figure 2

Approximating quantum gates Uθ by braiding Fibonacci anyons.

In the plotting, time flows from left to right, U1 represents Uπ/6 and U2 represents U−π/3.

Full size image