Abstract
Housing markets play a crucial role in economies and the collapse of a real-estate bubble usually destabilizes the financial system and causes economic recessions. We investigate the systemic risk and spatiotemporal dynamics of the US housing market (1975–2011) at the state level based on the Random Matrix Theory (RMT). We identify richer economic information in the largest eigenvalues deviating from RMT predictions for the housing market than for stock markets and find that the component signs of the eigenvectors contain either geographical information or the extent of differences in house price growth rates or both. By looking at the evolution of different quantities such as eigenvalues and eigenvectors, we find that the US housing market experienced six different regimes, which is consistent with the evolution of state clusters identified by the box clustering algorithm and the consensus clustering algorithm on the partial correlation matrices. We find that dramatic increases in the systemic risk are usually accompanied by regime shifts, which provide a means of early detection of housing bubbles.
Similar content being viewed by others
Introduction
Because houses and apartments are tradeable and are commonly used in speculations, they are considered as a special kind of commodity. As time passes the house prices boom and bust. Because the housing market is closely related to the financial system and plays a crucial role in economies, a crash of the housing market usually has disastrous consequences, causing financial crisis and economic recession. Recent examples include the 1997–1998 Asian crisis1,2,3 and the 2007–2012 global financial tsunami followed by the 2008–2012 global recession and the European sovereign-debt crisis, none of which has ended4. When the correlations among the constituents of a market become stronger and the ripple effect increases5, prices tend to converge6 and the systemic risk increases. However, there is evidence showing that alternative measures based on eigenvalues and eigenvectors of the correlation matrix outperform the average correlation in characterizing market integration7, quantifying systemic risks measured by means of the absorption ratio8 and constructing profitable investment portfolios8,9. Hence, it is extremely important to understand the spatiotemporal dynamics of housing markets through an investigation of the correlation matrix of price growth rates.
The correlation matrices of stock returns and indices have been widely studied in different markets10. The studies have employed variety of methods ranging from the minimal spanning trees11, the planar maximally filtered graph12 based on distance matrices, to RMT13,14. All methods can be used to identify constituent clusters in financial systems10. When RMT is used to investigate the correlation structure of financial markets, the largest eigenvalue serves to explain the collective behavior of the market and other eigenvalues are commonly used to explain clustering of stocks or indices into groups with specific traits.
The correlation matrices of housing markets are rarely studied, mainly due to the short length of house price indices, where the sampling frequency is usually either monthly or quarterly. Using the RMT framework at the state level, we investigate the spatiotemporal dynamics of the US housing market. We analyze the All-Transactions Indices of the 50 states and the District of Columbia published by the Federal Housing Finance Agency, which estimate sales prices and appraisal data. The data are recorded quarterly from 1975/Q1 to 2011/Q4, giving a total of 148 values.
We denote Si(t) the quarterly housing price index (HPI) of US state i at time t. The logarithmic return at time t is defined as

For each moving window [t − s + 1, t] at time t of size s, we compute the correlation matrix C(t), whose element Cij is the Pearson correlation coefficient between the return time series of US states i and j,

where μi and μj are the sample means and σi and σj are the standard deviations of the two states i and j respectively.
Stock markets are characterized by both fast and slow dynamics15,16. To estimate the empirical correlation matrix and minimize the unavoidable statistical uncertainty, we use a large window containing a large number of data points. Although large windows reduce our ability to investigate the fast dynamics in correlation studies, the correlation matrix is no longer invertible8,16 when the window size is smaller than the 51 time series in our study (50 states + DC), implying smin = 51. We set the value at s = 60 quarters, giving us 89 moving windows for investigation.
Results
Correlation coefficient
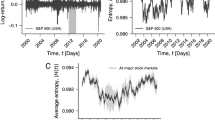
Figure 1A shows the average correlation coefficient of Eq. 2 calculated for each year during the last two decades. In recent years the average correlation coefficient has sharply increased indicating that the US housing market has become strongly correlated. In the early years of the period studied, we find that only a small number of states exhibit correlated housing indices. In contrast, we find a sharp increase in housing market correlations over the past decade, indicating that systemic market risk has also greatly increased.
Evolution of correlation coefficient, deviating eigenvalues and absorption ratio.
(a) Evolution of the average correlation coefficient. The horizontal red line shows the critical value at significance level 5% of the correlation coefficient at each time t. The error bar is the standard deviation of the PDF at each time t. For the evolution of the PDF, see Fig. S1. (b) Evolution of the five largest eigenvalues λn of C(t) with n = 1, 2, 3, 4 and 5. The horizontal dot-dashed red line is the maximum eigenvalue λmax predicted by the RMT and the horizontal red line represents the critical values λ5% at the significance level of 5%. The five vertical dashed lines corresponding to the five regime-shift points. (c) Evolution of absorption ratio En(t) for n = 1, 2, 3, 4 and 5.
Eigenvalues
An important topic in economic theory is whether housing market bubbles and financial bubbles in general are predictable. Figure 1B shows that the largest eigenvalue λ1 of C(t) has trended upward since 1993. Note also that λ1 sharply increased in 2008, coinciding with the bursting of the real estate bubble and the world-wide financial crisis of 2007–2010. Figure 1B shows that the largest eigenvalue λ1 of C(t) is larger than the maximum eigenvalue λmax predicted by the RMT and is also larger than the critical value λ5% of fRnd(λ) (see Methods). For the second largest eigenvalue, we find λ2 > λmax for all C(t) matrices and λ2 > λ5% for most C(t) matrices. We also find that the third largest eigenvalue λ3 is larger than λmax and λ5% for most C(t) matrices and the fourth largest eigenvalue λ4 is larger than λmax and λ5% for part of the C(t) matrices. In contrast, the fifth largest eigenvalue λ5 falls well within the range of fRMT(λ) and fRnd(λ) (Fig. S2). The eigenvalues λ1, λ2 and λ3 should thus contain information about nontrivial spatiotemporal properties of the US housing market dynamics. We also include λ4 in our investigation.
In addition to using the average correlation coefficient we can also measure systemic risk using the absorption ratio  , which is a better approach because perfectly integrated markets can exhibit weak correlation7,8,9. Figure 1C shows the absorption ratio. Note that the increase in systemic risk is approximately linear, even during the burst of the housing bubble in 2007, indicating that the US housing market continues to be fragile and unstable.
, which is a better approach because perfectly integrated markets can exhibit weak correlation7,8,9. Figure 1C shows the absorption ratio. Note that the increase in systemic risk is approximately linear, even during the burst of the housing bubble in 2007, indicating that the US housing market continues to be fragile and unstable.
Collective market effect and regime shifts
To investigate the possible collective market effect embedded in the deviating eigenvalues, we compare the returns of the eigenportfolio with the US HPI returns (see Methods). Before we proceed with the results for the housing market, we note that for stock markets k1 ≠ 0 and usually k1 → 1 and that kn ≈ 0 for n > 118. Thus although the largest eigenvalue reflects the behavior of the stock market, the other eigenvalues do not.
In the following, we report that the RMT results obtained for the US housing market (Fig. 2 and Fig. S3), which differ substantially from the results obtained for stock markets. For the housing market, we observe that the correlation coefficient k1 between R(t′) and R1(t′) is large for the first four years and then drops from 0.8354 (1993Q3) to 0.0655 (1993Q4). Then λ1 gradually increases to 0.8826 (2002Q2) and 0.9593 (2002Q3) and remains close to 1. This behavior for λ1 over time indicates that we can approximately identify three regimes for three time periods: [1989Q4, 1993Q3], [1993Q4, 2002Q2] and [2002Q3, 2011Q4] (see Methods). We find that the two regime-shift points in Fig. 2(a) virtually overlap with the first two local minima in the time dependence of λ1 in Fig. 1. Therefore, in the regimes corresponding to the first and last time periods, the market effect quantified by the correlation coefficient k1 is remarkable. In contrast, the market effect is much weaker in the second time period (Fig. S3). Within the second time period, we further identify a regime-shift point between 1997Q1 and 1997Q2, where k1 drops from 0.6955 to 0.5879.
Market effect hidden in the largest eigenvalues.
Each plot shows the evolution of the correlation coefficient kn(t) between Rn and R in each moving window. The blue symbols are estimated using ordinary least-squares linear regression, while the red ones are estimated using robust fitting. The four vertical lines indicate four regime-shift points  between 1993Q3 and 1993Q4,
between 1993Q3 and 1993Q4,  between 1997Q1 and 1997Q2,
between 1997Q1 and 1997Q2,  between 1999Q2 and 1999Q3 and
between 1999Q2 and 1999Q3 and  between 2002Q2 and 2002Q3, separating five different regimes. The shading area in each plot means that the associated eigenvalue contains a market effect in the corresponding time period. See Fig. S3 for the scatter plots of Rn against R.
between 2002Q2 and 2002Q3, separating five different regimes. The shading area in each plot means that the associated eigenvalue contains a market effect in the corresponding time period. See Fig. S3 for the scatter plots of Rn against R.
Figure 2(b) shows three regime shifts: 1993Q3–1993Q4, 1997Q1–1997Q2 and 2002Q2–2002Q3, which, surprisingly, are identical to those we found for λ1. Figure 2(c) shows two regime shifts for the third largest eigenvalue λ3: 1993Q3–1993Q4 and 1997Q1–1997Q2, which correspond to the first and second regime shifts found in eigenvalues λ1 and λ2. Figure 2(d) shows three regime shifts for the fourth largest eigenvalue λ4: 1993Q3–1993Q4, 1999Q2–1999Q3 and 2002Q2–2002Q3, the first and third of which correspond to those found for eigenvalues λ1 and λ2.
Using the four regime shifts in Figs. 2(a)–2(d), we identify five eigenvalue regimes:  ,
,  ,
,  ,
,  and
and  , which reveal an interesting US housing market dynamic. The five regimes are separated by four regime shift points:
, which reveal an interesting US housing market dynamic. The five regimes are separated by four regime shift points:  between 1993Q3 and 1993Q4,
between 1993Q3 and 1993Q4,  between 1997Q1 and 1997Q2,
between 1997Q1 and 1997Q2,  between 1999Q2 and 1999Q3 and
between 1999Q2 and 1999Q3 and  between 2002Q2 and 2002Q3, where
between 2002Q2 and 2002Q3, where  is visible in the evolution of k1, k2, k3 and k4,
is visible in the evolution of k1, k2, k3 and k4,  is visible in the evolution of k1, k2 and k3,
is visible in the evolution of k1, k2 and k3,  is visible only in the evolution of k4 and
is visible only in the evolution of k4 and  is visible in the evolution of k1, k2 and k4. The cross-validation of the four regime shift points in the four plots of Fig. 2 indicates that our identification of the different regimes is valid.
is visible in the evolution of k1, k2 and k4. The cross-validation of the four regime shift points in the four plots of Fig. 2 indicates that our identification of the different regimes is valid.
We find that in regime  , only for the largest eigenvalue λ1 is the market effect–quantified by the correlation coefficient k1 between R(t′) and R1(t′)–substantially large (Fig. S3). In regime
, only for the largest eigenvalue λ1 is the market effect–quantified by the correlation coefficient k1 between R(t′) and R1(t′)–substantially large (Fig. S3). In regime  , the market effect for λ1 becomes substantially weaker than in regime
, the market effect for λ1 becomes substantially weaker than in regime  and λ3 exhibits a moderately stronger market effect only at some time t (Fig. S3). In regime
and λ3 exhibits a moderately stronger market effect only at some time t (Fig. S3). In regime  , λ1 and λ2 exhibit a substantially stronger market effect than λ3 and λ4. In regime
, λ1 and λ2 exhibit a substantially stronger market effect than λ3 and λ4. In regime  , λ1, λ2 and λ4 exhibit a strong market effect. Finally, in regime
, λ1, λ2 and λ4 exhibit a strong market effect. Finally, in regime  , only λ1 exhibits a strong market effect, while the rest of eigenvalues λ2 − λ4 do not. We thus find that the largest eigenvalue λ1 almost always exhibits a market effect, whereas the other eigenvalues exhibit a market effect only infrequently, especially when the market effect becomes weak in λ1.
, only λ1 exhibits a strong market effect, while the rest of eigenvalues λ2 − λ4 do not. We thus find that the largest eigenvalue λ1 almost always exhibits a market effect, whereas the other eigenvalues exhibit a market effect only infrequently, especially when the market effect becomes weak in λ1.
Information contained in the eigenvectors associated with the largest eigenvalues
We find that the components of the eigenvector of the largest eigenvalue are positive in stock markets when the components exhibit small fluctuations over time, indicating a market effect. The rest of the eigenvectors of other largest eigenvalues describe different clusters of stocks or industrial sectors18,19,20. For the US housing market, we find that the eigenvectors of the largest eigenvalues contain much richer information (Fig. 3 and Fig. S4). The existence of five regimes  to
to  is clear and the eigenvector components persist in each regime (see Methods). Moreover, the graphical approach in Fig. 3 reveals that the regime
is clear and the eigenvector components persist in each regime (see Methods). Moreover, the graphical approach in Fig. 3 reveals that the regime  can be separated into two regimes at 2007Q1 to 2007Q2 according to the evolution of u3.
can be separated into two regimes at 2007Q1 to 2007Q2 according to the evolution of u3.
Starting with the first eigenvector u1, we study its components over time for different regimes. We find that in regime  almost all the components of u1 are positive. In contrast, Fig. 3 clearly shows that after 1993Q4 and during the three regimes
almost all the components of u1 are positive. In contrast, Fig. 3 clearly shows that after 1993Q4 and during the three regimes  to
to  many components of the first eigenvector u1 turn from positive to negative. During the period from 1993Q4 to 2002Q2, positive components of u1 approximately correspond to the states in the Eastern half of the US and with California and Arizona in the Western US. It means that the largest eigenvalue λ1 partitions the states into two groups. Because the states with positive components are predominantly the states with high HPI values, λ1 still exhibits a modest market effect. As time passes, transferring from regime
many components of the first eigenvector u1 turn from positive to negative. During the period from 1993Q4 to 2002Q2, positive components of u1 approximately correspond to the states in the Eastern half of the US and with California and Arizona in the Western US. It means that the largest eigenvalue λ1 partitions the states into two groups. Because the states with positive components are predominantly the states with high HPI values, λ1 still exhibits a modest market effect. As time passes, transferring from regime  to regime
to regime  , states with initially negative components turn from negative to positive components.
, states with initially negative components turn from negative to positive components.
For the eigenvector u2 in the first two regimes  and
and  we find a comparable number of negligible positive and negative components and it is not completely clear what information is contained in the US states with positive and negative components. At approximately 1997Q2 the number of states with negative u2 components drop significantly, leaving the majority of states with positive components that reflect a market effect. This predomination of positive components over negative components persists in
we find a comparable number of negligible positive and negative components and it is not completely clear what information is contained in the US states with positive and negative components. At approximately 1997Q2 the number of states with negative u2 components drop significantly, leaving the majority of states with positive components that reflect a market effect. This predomination of positive components over negative components persists in  and
and  . Beginning in late
. Beginning in late  , the u2 components of Washington and California switch from positive to negative and a few Northeastern states do the same. In regime
, the u2 components of Washington and California switch from positive to negative and a few Northeastern states do the same. In regime  , the two state clusters, one with positive and the other with negative u2 components, approximately correspond to states with low and high HPI growth rates, respectively, as identified by the super-exponential growth model21.
, the two state clusters, one with positive and the other with negative u2 components, approximately correspond to states with low and high HPI growth rates, respectively, as identified by the super-exponential growth model21.
In the evolution of the eigenvector u3, we find two interesting features. First, the majority of states in regime  have positive components, reflecting a modest market effect. Second, there is an evident subregime around 2007Q2, which surprisingly corresponds to the onset of the primary US mortgage crisis. The information contained in other regimes is ambiguous and it is difficult to extract clear information from the evolution of the fourth eigenvector u4.
have positive components, reflecting a modest market effect. Second, there is an evident subregime around 2007Q2, which surprisingly corresponds to the onset of the primary US mortgage crisis. The information contained in other regimes is ambiguous and it is difficult to extract clear information from the evolution of the fourth eigenvector u4.
Evolution of state clusters
To better understand the spatiotemporal dynamics of the US housing market at the state level, we partition the states into clusters for each time t. Because there is a strong market effect in the correlation matrices, the Pearson correlation coefficient between the return time series ri and rj of two US states i and j may not reflect their intrinsic relationship, but may reflect the influence of the overall US HPI return rus on i and j22,23. We thus utilize a clustering algorithm that uses the corresponding partial correlation matrices P(t) by removing the market effect. In this way we obtain a partial correlation matrix P(t) and an affinity A(t) for each t (see Methods).
For each t, we rearrange the order of states in P(t) and C(t) to be the same as in A(t). The evolution of the three matrices is illustrated in Fig. S5. In the early years represented by regions  and
and  , we identify the state clusters (Fig. 4(a)) in which the number of states forming each cluster is relatively small (Fig. 4(b)) and the constituent states of the clusters are unstable (Fig. S5). These properties are consistent with the fact that the average cross-correlation level among US states is very low, indicating that the housing markets of different US states are to some extent isolated. With the development of the US housing market during the period 1996Q4–2002Q1, more US states enter two different clusters of significantly different sizes (Fig. 4(b)). This period roughly corresponds to the two regimes
, we identify the state clusters (Fig. 4(a)) in which the number of states forming each cluster is relatively small (Fig. 4(b)) and the constituent states of the clusters are unstable (Fig. S5). These properties are consistent with the fact that the average cross-correlation level among US states is very low, indicating that the housing markets of different US states are to some extent isolated. With the development of the US housing market during the period 1996Q4–2002Q1, more US states enter two different clusters of significantly different sizes (Fig. 4(b)). This period roughly corresponds to the two regimes  and
and  . During this period both clusters are relatively stable (Fig. 4(b) and Fig. S5). In regime
. During this period both clusters are relatively stable (Fig. 4(b) and Fig. S5). In regime  the smaller cluster further splits into two even smaller clusters which remain relatively stable. At approximately 2007Q2 the larger cluster splits into two clusters of comparable size, but shortly after the two smaller clusters merge back into one (Fig. S5). Finally we find three stable clusters of similar size that form the sixth regime
the smaller cluster further splits into two even smaller clusters which remain relatively stable. At approximately 2007Q2 the larger cluster splits into two clusters of comparable size, but shortly after the two smaller clusters merge back into one (Fig. S5). Finally we find three stable clusters of similar size that form the sixth regime  .
.
Evolution of the states' clusters.
(a) Typical affinity matrices A(t) (left column), partial correlation matrices P(t) (middle column) and correlation matrices C(t) (right column). The order of the states is the same for the three matrices in each row. The ending quarters t of the windows from top to bottom are 1989Q4, 1992Q2, 1997Q4, 2006Q3 and 2011Q3. (b) Number of clusters Nc(t) and the corresponding number Ns(t) of states included in the detected clusters for each window. (c) Evolution of modularity M(t) and the squared sum V(t) of negative components in λ1(t). (d) Maximal information ratio G(λn) of certain eigenvalue λn contributed to a cluster. Each cluster is represented by a colorful symbol. The determination of symbols and their coloring is explained in Methods. (e) Evolution of states clusters, where the order of the states is the same as A(t) at t = 2009Q3. The states in a certain cluster are assigned with a cluster-specific colorful symbol and no symbol is assigned to those states not in any cluster. The colorful symbols have the same meaning as those in (d).
For each window t there are up to four clusters of states and the number of states in each cluster varies from one window to the next. For each cluster, one of the four deviating eigenvalues makes a dominant contribution (Fig. 4(d)). We find that in regimes  and
and  the largest eigenvalue λ1 participates in the cluster partitioning.
the largest eigenvalue λ1 participates in the cluster partitioning.
Figure 4(e) shows the spatiotemporal dynamics of the state clusters. The states in the red cluster tend to have larger price fluctuations (and a higher price value) and the states in the green cluster exhibit smaller HPI growth rate fluctuations (Fig. S6). In the earlier years ( and
and  ) the clusters are unstable with a large number of states shifting between clusters. During this period, the primary contribution to the green cluster comes from the third largest eigenvalue λ3. In contrast, there are more eigenvalues contributing to the red cluster. In 1997 we find that two rapidly-forming large stable green and red clusters are dominated by λ2 and λ1, respectively. This phase-transition-like phenomenon in 1997 may have been evidence of a fast ripple effect within the US housing market. After 2005Q2 the red cluster splits into two smaller clusters for approximately two years and almost all of the clusters are dominated by λ2. Beginning in 2007Q2 the green cluster partitions into two smaller clusters: the red and green clusters are still dominated by λ2 and the new yellow cluster is dominated by λ3. The time period of these two transitions corresponds to the downturn in the US housing market. In short, Fig. 4(e) shows the extreme complexity of the spatiotemporal dynamics of the US housing market.
) the clusters are unstable with a large number of states shifting between clusters. During this period, the primary contribution to the green cluster comes from the third largest eigenvalue λ3. In contrast, there are more eigenvalues contributing to the red cluster. In 1997 we find that two rapidly-forming large stable green and red clusters are dominated by λ2 and λ1, respectively. This phase-transition-like phenomenon in 1997 may have been evidence of a fast ripple effect within the US housing market. After 2005Q2 the red cluster splits into two smaller clusters for approximately two years and almost all of the clusters are dominated by λ2. Beginning in 2007Q2 the green cluster partitions into two smaller clusters: the red and green clusters are still dominated by λ2 and the new yellow cluster is dominated by λ3. The time period of these two transitions corresponds to the downturn in the US housing market. In short, Fig. 4(e) shows the extreme complexity of the spatiotemporal dynamics of the US housing market.
In order to achieve a finer resolution as we characterize systemic risk, we divide the 51 time series into six clusters according to the state clusters shown in Fig. 4(e). We form a sample with six return time series, each being randomly chosen from a cluster. We use a moving window of eight quarters (two years) size to determine the eigenvalues of the correlation matrices of the sample. We repeat this procedure 50 times and average the corresponding eigenvalues. We find that the systemic risk increases sharply in the early 1990s and drops to a relatively low level in late 1990s (Fig. S7). The absorption ratio increases dramatically in 2003 and remains historically high. Unlike the results of an analysis of 14 metropolitan housing markets in the United States9, our analysis shows that the systemic risk is still at historically high levels after the housing bubble peaks.
Discussion
Using random matrix theory, we have investigated the complex spatiotemporal dynamics of the US housing market at the state level. Using long timescales, we divide the evolution of the market into three time periods. During the first time period (1989Q4 to 1997Q1) the market exhibits a low correlation, the largest eigenvalue reflects a market effect and the next three largest eigenvalues contain partitioning information. During the second time period (1997Q2 to 2002Q2) the correlation among the states is still low and the market effect of the largest eigenvalue becomes weaker. We find that the largest eigenvalue contains partitioning information and that the deviating eigenvalues exhibit a weak market effect. During the last period, the largest eigenvalue exhibits a strong market effect and its partitioning function disappears, which corresponds to the fact that market integration has become significantly stronger and exhibits sharply increasing average correlations. During this period, the partitioning of the states is primarily caused by the second largest eigenvalue. After the subprime crisis, the third largest eigenvalue exhibits a partitioning function.
These regime shifts reflect the abrupt increases in systemic risk that took place in the US housing market. Figures 4(b) and 4(d) show that in 1997 most states were gathered into two clusters. Thus we conjecture that the housing bubble that burst in 2007 had begun to inflate as early as 1997. This finding is consistent with and provides convincing evidence for our conclusion based on the evolution of the absorption ratio9.
Note that there are both positive and negative components in the eigenvectors of the deviating eigenvalues for most time windows. When the components of an eigenvector have the same sign, it usually reflects a market effect. When an eigenvector has both positive and negative components, especially when their amounts are comparable, the eigenvector may reflect either geographical information or differences in house price growth rates or both. The information contained in the signs of the eigenvector components has recently been reported for stock markets27,28,29. However, the US housing market appears more complex than stock markets.
During the evolution of the US housing market, we observe that prices diffuse in complex ways that do not require geographical clusters30. This differs from worldwide stock markets, which exhibits clear geographical clustering16. The splitting and merging of clusters indicate that there is no national convergence of house prices. Furthermore, the model in Ref. 6, in which there are several clusters within which the prices converge is too simple, so we have used a different approach for state clustering. We thus conjecture that there are different classifications for converging clusters in different time periods.
Methods
Determining deviating eigenvalues
For each t larger or equal to t = 1990/Q1, we calculate the correlation matrix C(t) and compute its 51 eigenvalues  . Then we sort the eigenvalues {λn} in descending order and calculate the corresponding eigenvectors
. Then we sort the eigenvalues {λn} in descending order and calculate the corresponding eigenvectors  .
.
If M is a T × N matrix with mean 0 and variance σ2 = 1, we define  . In the limit N → ∞, T → ∞ where Q = T/N ≥ 1 is fixed, the probability density fRMT(λ) of eigenvalues λ of matrix C is
. In the limit N → ∞, T → ∞ where Q = T/N ≥ 1 is fixed, the probability density fRMT(λ) of eigenvalues λ of matrix C is  , where λ ∈ [λmin, λmax] and
, where λ ∈ [λmin, λmax] and  17,13,18. If an eigenvalue λ is greater than λmax–and thus deviates from the prediction of the RMT–its eigenvector frequently contains valuable information about market dynamics.
17,13,18. If an eigenvalue λ is greater than λmax–and thus deviates from the prediction of the RMT–its eigenvector frequently contains valuable information about market dynamics.
In real-world data, however, the limit conditions N → ∞ and T → ∞ are never fulfilled and some finite-size effect should be included in the RMT studies. In order to identify the deviating eigenvalues, we thus randomize the housing index time series to eliminate any temporal correlations. We then calculate a new correlation matrix CRnd from the randomized return time series and compute the corresponding 51 eigenvalues. Repeating this procedure 1000 times we obtain a total of 51,000 eigenvalues based on which we calculate the probability density of eigenvalues fRnd(λ). Although the density functions fRMT(λ) and fRnd(λ) overlap to a great degree, they exhibit some differences in the right-hand tail. We find that fRnd(λ) is not bounded by the maximum eigenvalue λmax predicted by the RMT (Fig. S2). This is the case because the HPI returns have fat tails. We retain only the eigenvalues that come from the distribution fRnd(λ) with a probability smaller than 5% and we denote the critical value to be λ5%.
Construction of eigenportfolio
For each eigenvalue λn we construct its eigenportfolio, the returns of which we calculate by

where  and
and  is a vector whose components are state-level HPI returns defined in Eq. 1. To evaluate the collective market effect embedded in λn, we investigate the following linear regressive model between Rn(t′) and the return R(t′) of the US HPI
is a vector whose components are state-level HPI returns defined in Eq. 1. To evaluate the collective market effect embedded in λn, we investigate the following linear regressive model between Rn(t′) and the return R(t′) of the US HPI

where Rn and R are normalized respectively to zero mean and unit variance18 and kn(t) is the correlation coefficient between Rn and R in time t′. If kn differs significantly from 0, we assume the eigenvalue λn contains a market effect because the corresponding eigenportfolio is correlated with the entire market18. The market effect is stronger if kn is larger. To estimate the value of kn, we perform an ordinary least-squares (OLS) linear regression together with a robust regression. Since the results and conclusions for both methods are qualitatively the same, we limit our discussion to the OLS results.
Partial correlations and state clustering
The partial correlation coefficient Pij between ri and rj with respect to rus can be calculated24,23

where Ci,us (Cj,us) is the Pearson correlation coefficient between ri (rj) and rus. For each partial correlation matrix P(t), we combine the box clustering and consensus clustering methods to search for clusters of states25,26. We first determine the optimal ordering of P(t) by identifying the largest elements in P(t) close to the diagonal, where the simulated annealing approach is adopted to minimize the cost function

We then use a greedy algorithm to partition clusters of states and isolated states25. We repeat this procedure 200 times and obtain 200 partitions. We construct an affinity matrix A′ whose element  is the number of partitions in which i and j are assigned to the same cluster, divided by the number of partitions 200. Finally we apply the clustering method to the affinity matrix A′, resulting in a final partition A(t)26. For each t, we rearrange the order of states in P(t) and C(t) to be the same as in A(t).
is the number of partitions in which i and j are assigned to the same cluster, divided by the number of partitions 200. Finally we apply the clustering method to the affinity matrix A′, resulting in a final partition A(t)26. For each t, we rearrange the order of states in P(t) and C(t) to be the same as in A(t).
Identification of different regimes
To identify different regimes, we locate abrupt changes in the evolution of different variables. The first class of variables is the degree of market effect quantified by kn for the deviating eigenvalues as shown in Fig. 2. If the absolute change |kn(t + 1) − kn(t)| is significantly greater than the average of the absolute changes around t, t is identified as a possible regime-shifting point. For the evolution of eigenvectors in Fig. 3, if there appears to be significantly less similarity between two successive eigenvectors un(t) and un(t + 1), t is a possible regime-shifting point. This similarity criterion can also be applied to the evolution of state clusters as shown in Fig. 4(e). If the identified regime-shifting points overlap, their presence is more convincing. Comparing the results from different variables can thus serve as a method of cross-validation. Thus to design a reliable method of regime identification we clearly need to construct mathematical models that include the kind of regime-shifting seen in the US housing market.
Determination of symbols in Fig. 4(d)
We assign the symbol for each cluster according to the contribution made by the eigenvalues. Note that the correlation matrix C(t) can be decomposed as31,32

where  is the matrix associated with λn and its element is
is the matrix associated with λn and its element is  . We define the information ratio of λn in a certain cluster
. We define the information ratio of λn in a certain cluster  as
as

which is the relative contribution of λn to  and the maximum information ratio G(λn) can be easily determined. Since almost all the components of u1 are positive in regimes
and the maximum information ratio G(λn) can be easily determined. Since almost all the components of u1 are positive in regimes  ,
,  and
and  (Fig. 4(c)), the partitioning function of λ1 is weak. In these time periods, the modularity defined in Ref. 33, 34 is also relatively small. We thus exclude λ1 from the determination of G(λn) in these three regimes. If λn(t) makes the largest contribution to cluster
(Fig. 4(c)), the partitioning function of λ1 is weak. In these time periods, the modularity defined in Ref. 33, 34 is also relatively small. We thus exclude λ1 from the determination of G(λn) in these three regimes. If λn(t) makes the largest contribution to cluster  (i.e.,
(i.e.,  is maximal), then an eigenvalue-specific symbol is assigned to
is maximal), then an eigenvalue-specific symbol is assigned to  : circle (
: circle ( ) for λ1, square (
) for λ1, square ( ) for λ2, diamond (
) for λ2, diamond ( ) for λ3 and triangle (
) for λ3 and triangle ( ) for λ4.
) for λ4.
Coloring the states in Fig. 4(e)
For a given time t, states belonging to the same cluster are marked with the same color and states belonging to different clusters are marked with different colors. For the sake of simplicity, we define for each t a color configuration vector Φt, the elements of which correspond to the 51 states in a predetermined order. The elements of Φt corresponding to each cluster are assigned a unique positive integer and the remaining elements not belonging to a cluster are assigned zeros. For two configurations Φt and Φt′, we define a measure of similarity J,

where δx,y is the Kronecker delta function, which is equal to 1 if x = y and 0 otherwise. The ultimate task of globally maximizing  is impossible since the number of the parameters in Fig. 4(b) is too large.
is impossible since the number of the parameters in Fig. 4(b) is too large.
To solve the coloring problem, we adopt a heuristic algorithm. We determine the colors of the clusters in reverse from 2011Q4 to 1989Q4. We separate the time period into two intervals: I1 = [1989Q4, 1996Q1] and I2 = [1996Q2, 2011Q4]. For t = 2011Q4 there are three clusters of states colored yellow, green and red. As we determine Φt for a given t ∈ I2, all Φt′ with t′ > t are already determined. The configuration Φt is determined by maximizing  , where t′ = min{6Q, 2011Q4 − t}. When t ∈ I1, we maximize
, where t′ = min{6Q, 2011Q4 − t}. When t ∈ I1, we maximize  . Note that small alterations in the assigned future reference configuration does not affect the results.
. Note that small alterations in the assigned future reference configuration does not affect the results.
References
Kaminsky, G. L. & Reinhart, C. M. The twin crises: The causes of banking and balance-of-payments problems. Amer. Econ. Rev. 89, 473–500 (2012).
Quigley, J. A. Real estate and the Asian crisis. J. Housing Econ. 10, 129–161 (2001).
Fung, K.-K. & Forrest, R. Institutional mediation, the Hong Kong residential housing market and the Asian Financial Crisis. Housing Stud. 17, 189–207 (2002).
Sanders, A. The subprime crisis and its role in the financial crisis. J. Housing Econ. 17, 254–261 (2008).
Giussani, B. & Hadjimatheou, G. Modeling regional house prices in the United Kingdom. Pap. Reg. Sci. 70, 201–219 (1991).
Kim, Y. S. & Rous, J. J. House price convergence: Evidence from US state and metropolitan area panels. J. Housing Econ. 21, 169–186 (2012).
Pukthuanthong, K. & Roll, R. Global market integration: An alternative measure and its application. J. Financial Econ. 94, 214–232 (2009).
Billio, M., Getmansky, M., Lo, A. W. & Pelizzon, L. Econometric measures of systemic risk in the finance and insurance sectors. J. Financial Econ. 104, 535–559 (2012).
Kritzman, M., Li, Y.-Z., Page, S. & Rigobon, R. Principal components as a measure of systemic risk. J. Portf. Manag. 37, 112–126 (2011).
Tumminello, M., Lillo, F. & Mantegna, R. N. Correlation, hierarchies and networks in financial markets. J. Econ. Behav. Org. 75, 40–58 (2010).
Mantegna, R. N. Hierarchical structure in financial markets. Eur. Phys. J. B 11, 193–197 (1999).
Tumminello, M., Aste, T., Di Matteo, T. & Mantegna, R. N. A tool for filtering information in complex systems. Proc. Natl. Acad. Sci. U.S.A. 102, 10421–10426 (2005).
Laloux, L., Cizeau, P., Bouchaud, J.-P. & Potters, M. Noise dressing of financial correlation matrices. Phys. Rev. Lett. 83, 1467–1470 (1999).
Plerou, V., Gopikrishnan, P., Rosenow, B., Amaral, L. A. N. & Stanley, H. E. Universal and nonuniversal properties of cross correlations in financial time series. Phys. Rev. Lett. 83, 1471–1474 (1999).
Drozdz, S., Grümmer, F., Gorski, A. Z., Ruf, F. & Speth, J. Dynamics of competition between collectivity and noise in the stock market. Physica A 287, 440–449 (2000).
Song, D.-M., Tumminello, M., Zhou, W.-X. & Mantegna, R. Evolution of worldwide stock markets, correlation structure and correlation based graphs. Phys. Rev. E 84, 026108 (2011).
Sengupta, A. M. & Mitra, P. P. Distributions of singular values for some random matrices. Phys. Rev. E 60, 3389–3392 (1999).
Plerou, V. et al. Random matrix approach to cross correlations in financial data. Phys. Rev. E 65, 066126 (2002).
Pan, R. K. & Sinha, S. Collective behavior of stock price movements in an emerging market. Phys. Rev. E 76, 046116 (2007).
Shen, J. & Zheng, B. Cross-correlation in financial dynamics. EPL (Europhys. Lett.) 86, 48005 (2009).
Zhou, W.-X. & Sornette, D. Is there a real-estate bubble in the US? Physica A 361, 297–308 (2006).
Kenett, D. Y., Shapira, Y. & Ben-Jacob, E. RMT assessments of the market latent information embedded in the stocks' raw, normalized and partial correlations. J. Prob. Stat. 2009, 249370 (2009).
Kenett, D. Y. et al. Dominating clasp of the financial sector revealed by partial correlation analysis of the stock market. PLoS One 5, e15032 (2010).
Baba, K., Shibata, R. & Sibuya, M. Partial correlation and conditional correlation as measures of conditional independence. Aust. N. Z. J. Stat. 46, 657–664 (2004).
Sales-Pardo, M., Guimerà, R., Moreira, A. A. & Amaral, L. A. N. Extracting the hierarchical organization of complex systems. Proc. Natl. Acad. Sci. U.S.A. 104, 15224–15229 (2007).
Lancichinetti, A. & Fortunato, S. Consensus clustering in complex networks. Sci. Rep. 2, 336 (2012).
Yan, Y., Liu, M.-X., Zhu, X.-W. & Chen, X.-S. Principle fluctuation modes of the global stock market. Chin. Phys. Lett. 29, 028901 (2012).
Jiang, X.-F. & Zheng, B. Anti-correlation and subsector structure in financial systems. EPL (Europhys. Lett.) 97, 48006 (2012).
Junior, L. S. Cluster formation and evolution in networks of financial market indices. Algo. Fin. 2, 3–43 (2013).
Pollakowski, H. & Ray, T. Housing price diffusion patterns at different aggregation levels: An examination of housing market efficiency. J. Housing Res. 8, 107–124 (1997).
Noh, J. D. Model for correlations in stock markets. Phys. Rev. E 61, 5981–5982 (2000).
Kim, D. H. & Jeong, H. Systematic analysis of group identification in stock markets. Phys. Rev. E 72, 046133 (2005).
Newman, M. E. J. & Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 69, 026113 (2004).
Guimerà, R., Sales-Pardo, M. & Amaral, L. A. N. Modularity from fluctuations in random graphs and complex networks. Phys. Rev. E 70, 025101 (2004).
Acknowledgements
HM, WJX, ZQJ and WXZ received support from the National Natural Science Foundation of China Grant 11075054 and 71131007, the Shanghai (Follow-up) Rising Star Program Grant 11QH1400800, the Shanghai “Chen Guang” Project Grant 2012CG34 and Fundamental Research Funds for the Central Universities. BP and HES received support from the Defense Threat Reduction Agency (DTRA), the Office of Naval Research (ONR) and the National Science Foundation (NSF) Grant CMMI 1125290.
Author information
Authors and Affiliations
Contributions
B.P., W.X.Z. and H.E.S. conceived the study. H.M., W.J.X., Z.Q.J., B.P., W.X.Z. and H.E.S. designed and performed the research. H.M., W.J.X. and Z.Q.J. performed the statistical analysis of the data. B.P., W.X.Z. and H.E.S. wrote, reviewed and approved the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
SUPPLEMENTARY INFORMATION
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Meng, H., Xie, WJ., Jiang, ZQ. et al. Systemic risk and spatiotemporal dynamics of the US housing market. Sci Rep 4, 3655 (2014). https://doi.org/10.1038/srep03655
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03655
This article is cited by
-
Sentiment-based indicators of real estate market stress and systemic risk: international evidence
Annals of Finance (2023)
-
Portfolio Correlations in the Bank-Firm Credit Market of Japan
Computational Economics (2022)
-
Entropy of Graphs in Financial Markets
Computational Economics (2021)
-
An analysis of systemic risk in worldwide economic sentiment indices
Empirica (2020)
-
Correlation Structure and Evolution of World Stock Markets: Evidence from Pearson and Partial Correlation-Based Networks
Computational Economics (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

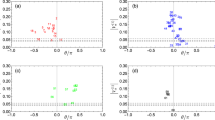



 to
to  are visible. Moreover, we observe that the regime
are visible. Moreover, we observe that the regime  can be separated into two regimes at 2007Q1 to 2007Q2 according to the evolution of u3.
can be separated into two regimes at 2007Q1 to 2007Q2 according to the evolution of u3.