Introduction

The desire for higher telecommunication bandwidth drives the quest for integrated photonic circuits. A key component of such circuits is the optical modulator1, which has been realized in a variety of ways. Modulators typically use one of three approaches, i.e. either the absorption of light2,3,4, a phase shift in conjunction with an interferometer5,6,7, or the shifting of a resonance8,9,10,11,12,13,14. In all of these realizations there is a tradeoff between the different properties of modulators: the speed at which they operate, their energy consumption, their optical bandwidth, their footprints and the ease with which they can be fabricated and integrated into existing circuits. For example, cavity based modulation is typically based on the shifting of extremely narrow resonances. Consequently, while such modulators allow for low energy consumption and fast operation, they are limited to very narrow optical bandwidths.

The tunability of the optical properties of two-dimensional photonic crystals (PhC) in conjunction with the maturity of silicon nanotechnology1, makes their use as compact, ultrafast active elements extremely attractive. Recently, optical injection of free-carriers15,16,17 in PhCs has enabled demonstrations of band-shifting18, phase-changes19 and frequency conversion20. In turn, these phenomena have been exploited for applications like directional couplers21, the tunable delay of pulses22 and modulators11,19,23. Proper dispersion engineering of photonic crystal waveguides, which enhances the light-matter interactions, has allowed for very compact24 and very fast devices25. However, the PhC based modulators demonstrated so far, mostly depend on an interferometric design and still required relatively large footprints. What is missing is a design that allows for devices with a smaller footprint, yet with broad wavelength operation.

Here we use ultrafast pump-probe measurements to show that, using a PhC waveguide, it is possible to create an optical amplitude modulator that operates in transmission and that fulfils these requirements. We show that by exploiting the slow-light nature of the PhC waveguide26,27, the footprint of the modulator can be reduced to an area of ~10 μm2 and that it is possible to significantly improve its performance. We offer a model that explains this surprising behaviour. Finally, we contrast our implementation with other realizations of optical modulators.

Results

Concept

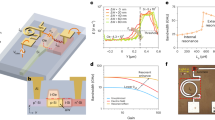
Our modulator, which we show schematically in Fig. 1a, is based on bandshifting. That is, if the PhC waveguide is unpumped a mode is available for an input signal pulse and it is transmitted. Conversely, a control pump pulse can be used to optically inject free-carriers which shift the bandedge so that the mode is no longer available at the frequency of the input pulse. This pulse would then be reflected. As the carriers decay, the bandstructure shifts back towards its original state, allowing the signal to be transmitted again.

Figure 1
figure 1

Dispersion engineered photonic crystal modulator.

(a) Schematic of the PhC modulator where the pumped area is represented by the yellow ellipse that covers the entire 80 μm waveguide or the red circle that covers a 3 μm section. The direction of the probe pulse is represented by the black arrow. (b) Calculated band structure of the unperturbed waveguide mode (Δn = 0) in blue and the perturbed waveguide mode (Δn = −0.01) in purple, with the ‘on’ and ‘off’ states labelled for a pulse centred at 1568 nm. (c) Group index of the waveguide mode as a function of freespace wavelength. The cyan dots represent the experimentally measured ng of the unperturbed waveguide, whereas the thin lines are the calculated group indices corresponding to the dispersion shown in (b).

Full size image

Bandshifting, however, is not the only effect in play. Signal light at wavelengths that are near the bandedge but too far away to be rejected by the bandshifting, experience strong changes in the group index (Fig. 1c). As we show later, a large increase in the group index in combination with the presence of free-carriers can result in sufficient absorption of the signal light to effectively turn the transmission off. And, even more interestingly, this interplay between free-carrier absorption and group index change, results in different dynamics for differently sized structures.

To demonstrate this modulator we use an 80 μm long dispersion-engineered PhC waveguide, where the size and positions of the holes near the waveguide have been altered to create a flatband slow-light region28,29,30. In other words, the waveguide mode has a spectral region such that a relatively broadband pulse will experience a high group index yet relatively little group velocity dispersion. Such flatband regions are necessarily located away from the bandedge of the PhC waveguide mode and as we show below, this spectral separation governs much of the modulation dynamics. Details on the design and fabrication can be found in ref. 31.

We present the calculated bandstructure of our unperturbed (nSi = 3.47, Δn = 0) silicon PhC waveguide in Fig. 1b with the blue line32. To represent the perturbed waveguide we calculate the bandstructure for nSi = 3.46 (i.e. Δn = −0.01). This bandstructure, indicated with the purple line in Fig. 1b, is blueshifted by ~4 nm with respect to the unperturbed bandstructure. This means that wavelengths in the range 1567 nm < λ < 1571 nm would be transmitted through the unperturbed waveguide, but would be reflected from the waveguide when Δn = −0.01, as demonstrated for λ = 1568 nm in Fig. 1b by the dashed gray line.

In Fig. 1c we show the calculated group index, ng, corresponding to the bandstructures shown in Fig. 1b, which we compare to our measured ng, obtained using an interferometric measurement scheme33. This experimentally determined ng of the unperturbed waveguide, which is depicted with cyan dots in Fig. 1c, is in good agreement with the calculated ng.

Experiment

To experimentally investigate the dynamics of our modulator we use a pump-probe scheme, where we either pump the full length of the waveguide (80 μm), or pump a 3 μm section. The time delay between the pump and the telecom probe pulse is varied to map the transient response of the modulator. Figure 2 depicts the transmission of the waveguide as a function of pump-probe delay, measured at several wavelengths and normalized by the unpumped waveguide. Figure 2a shows the transmission when the full waveguide is pumped. The absorbed fluence (averaged over the 80 μm long waveguide and the 4 neighbouring rows to each side of the PhC) is ~37 fJ/μm2, leading to an absorbed energy of ~8.8 pJ in the entire PhC waveguide.

Figure 2
figure 2

Dynamics of the modulator.

The transmission through the PhC waveguide as a function of the time delay for several different wavelengths, normalized by the transmitted intensity of the unpumped waveguide. (a) Transmission when the full length of the 80 μm waveguide is pumped. The absorbed energy is ~8.8 pJ. (b,c) Transmission when only a 3 μm section of the waveguide is pumped. The absorbed energy is ~0.9 pJ and ~2.0 pJ for (b) and (c) respectively. The solid gray lines indicate 35% and 70% transmission levels (3 dB ratio). The dotted black lines indicate 8% and 80% transmission levels (10 dB ratio). The green arrow in (a) illustrates the modulation time Δτ (for 1550 nm) as described in the Performance section of the text.

Full size image

The normalized transmission T at all the depicted wavelengths shows a sudden drop at zero time delay followed by a gradual recovery. The curious feature that T exceeds unity just before this drop is explained by the adiabatic frequency shifting of the probe pulse that occurs when the pump and the probe overlap in time20. The transmission of the shorter wavelengths drops to nonzero values and shows an immediate recovery whereas the transmission at the longest wavelengths drops to near-zero values and stays at this level for a couple hundred picoseconds before starting to recover.

This delay in recovery can be understood in terms of the pump induced shift of the bandstructure and of the modegap in particular. Light that is initially near the cutoff, in this case 1568 and 1569 nm, ends up in the modegap due to the pumping and is therefore reflected. As the bandstructure begins to shift back due to carrier recombination, the shorter wavelengths, furthest from the original modegap, will be the first to be transmitted again. The longer wavelengths, closest to the original modegap, will be rejected the longest.

However, as explained above, bandshifting is not the whole story. The transmission at 1550 and 1554 nm is also reduced when the PhC is pumped, yet the bandshift is too small for these wavelengths to end up in the modegap. Three other mechanisms influence the transmission: free-carrier absorption, back-scattering and out-of-plane scattering, which scale with ng, and ng respectively34,35. Although, as we will show later, the scattering losses turn out to be of less importance than the absorption losses.

These loss channels are the reason why the shorter wavelengths that are far away from the bandgap also exhibit a reduced transmission. To understand why the losses are higher for 1554 than for 1550 nm, we have to look at the group index. As can be seen in Fig. 1c, the group index of the pumped mode is almost twice as high at 1554 nm as it is at 1550 nm, resulting in higher absorption. For the longer wavelengths in Fig. 2a, where ng is much higher, the absorption and scattering losses will be even more significant, strongly influencing the dynamics of the recovery.

It is clear from Fig. 2a, that while the 80 μm long waveguide can act like an optical modulator, its behaviour is far from ideal. In particular, the transmission recovers very slowly and the losses due to free-carrier absorption are high. This suggests that a shorter waveguide will perform superiorly as our modulator. This can be achieved by simply pumping a smaller section of the same waveguide. We expect this to highlight the effect of the bandshift rather than that of the absorption and scattering. In Fig. 2b we present the transmission when only a 3 μm section of the waveguide is pumped, with an average absorbed fluence of ~100 fJ/μm2 leading to an absorbed energy of ~0.9 pJ. Although the absorbed fluence is almost 3 times higher than the case where the full waveguide is pumped, the absorbed energy is still 10 times lower than for the long modulator. In contrast to what we observed above (Fig. 2a), for the smaller pump spot the shortest wavelengths show very little losses, as a smaller total number of free-carriers are created, resulting in less absorption. The transmission at intermediate wavelengths (1566–1568 nm) drops to very low values but starts to recover immediately. Since these curves don't show the plateau at near-zero transmission, it is clear they are not being rejected by the mode-gap, but that their dynamics is governed by absorption losses. Transmission at 1569 nm drops to near-zero and remains there for ~100 ps before staring to recover. Clearly, pumping a smaller section results in lower absorption and, surprisingly, a quicker recovery. However, for the absorbed pump energy of 0.9 pJ only a very small wavelength range is suppressed to near-zero transmission. To suppress a larger range of wavelengths a higher pump energy is required.

In Fig. 2c we present the transmission when again a 3 μm section of the waveguide is pumped, but now with an average absorbed fluence of ~230 fJ/μm2 leading to an absorbed energy of ~2.0 pJ. The transmission drops to near-zero for a much broader range of wavelengths than in the case where the full waveguide was pumped, but for a much lower absorbed energy. Further, the transmission recovers earlier and occurs in a much steeper fashion. This, surprisingly, suggests that a shorter modulator outperforms a longer one.

Performance

To compare the performance of the different realizations of the modulator in a more quantitative manner, we first define the modulation time Δτ as the time between the moment T drops below a lower threshold (‘off’ level) until the moment it exceeds an upper threshold (‘on’ level) again. The horizontal pair of solid gray lines in Fig. 2 indicates ‘off–on’ levels of 35%–70% (i.e. a ratio of 3 dB) and the dotted black lines indicates 8%–80% (10 dB ratio). Figure 3 shows the optical bandwidth Δλ, defined as the maximum continuous wavelength range that is accessible for a given modulation time. The blue, green and black sets of curves correspond to the data shown in Fig. 2a, 2b and 2c respectively. The solid and dotted curves correspond to the pairs of ‘off’ and ‘on’ levels of the same line style in Fig. 2.

Figure 3
figure 3

The optical bandwidth Δλ that can be modulated for given Δτ.

Extracted from the data presented in Fig. 2. All solid curves are for an extinction ratio of 3 dB, the dotted curves are for an extinction ratio of 10 dB. (Δτ is described in the Performance section of the text).

Full size image

A global increase of Δλ as a function of Δτ time is observed, demonstrating the tradeoff between a short modulation time and a broad optical bandwidth. Comparing the different length modulators one can see that the long modulator (blue curve) is outperformed in Δλ by the short modulator (solid black curve) for the whole wavelength range. Even at lower absorbed energy (green curve), the short modulator allows for larger Δλ up to Δτ = 350 ps, yet it demonstrates significantly narrower wavelength operation than the 2.0 pJ case (solid black). When increasing the extinction ratio from 3 dB (solid curves) to 10 dB (dotted curve) the optical bandwidth is much narrower, but Δλ = 7 nm (5 nm) at Δτ = 500 ps (420 ps) can still be achieved for the 3 μm pump spot with an absorbed energy of 2.0 pJ (dotted black). However, an extinction ratio of 3 dB for the same pump spot (solid black) shows the best combination of optical bandwidth and modulation time with Δλ = 17 nm (14 nm) for Δτ = 480 ps (360 ps). This clearly demonstrates the benefit of pumping a smaller area, particulary considering the energy consumption is also much lower. Note that, at the cost of narrower optical bandwidth, higher insertion losses or a lower extinction ratio, smaller Δτ (down to 50 ps) could be achieved by a different choice of ‘off–on’ levels.

Model

To explain the dynamics of our modulator, we model our experiments as follows. The free-carrier concentration N follows directly from the absorbed fluence. Using the Drude model, the complex refractive index change of the silicon can be determined from N. For the concentrations that we are concerned with, scales linearly with N. The imaginary part of results in a free-carrier absorption coefficient αFC for the transmitted light and the real part, leads to a shift of the bandstructure. For the small Δn at which our device operates, the bandshift can be considered linear and constant for the wavelength range of interest. At wavelengths with low group velocity dispersion (λ < 1540 nm) the phase shift will be proportional to the bandshift. By measuring the dynamics of the phase shift in an interferometric measurement scheme, we can determine a carrier decay time of ~350 ps. We can now determine αFC and ng as a function of delay time and wavelength. The absorption of the probe light is enhanced by the group index. This may be interpreted as the slowdown of light increasing the effective length of the waveguide by ng/nSi. The normalized transmission T can then be modelled as follows:

where L is the length of the pumped waveguide section (see Supplementary section Model and parameters). Losses due to back-scattering and out-of-plane scattering are neglected in this model, as we found that these are much smaller than the losses due to free-carrier absorption.

The modelled normalized transmission through a waveguide of length L = 80 μm and L = 3 μm is shown in Fig. 4a and Fig. 4b respectively. The group indices and αFC are calculated for an absorbed fluence of 70 fJ/μm2 (resulting in Δn = −0.01). A free-carrier decay time of 350 ps is assumed for both cases. The dashed lines show the response of a spectral delta-peak and detail the response of a very narrowband source, the solid lines are transmission spectra that are convoluted with a 1 nm wide Gaussian to better represent our experiment.

Figure 4
figure 4

Modelled dynamics of the modulator.

Transmission as a function of time delay after pump pulse for several different wavelengths, normalized by the transmission of the unpumped waveguide. (a) Transmission when the full waveguide is pumped. (b) Transmission when only a 3 μm section is pumped. Both cases are modelled with the same absorbed pump fluence (70 fJ/μm2) and hence also the same refractive index change (Δn = −0.01). The dashed curves show the transmission of a spectral delta peak, the solid curves represent the response of a 1 nm wide Gaussian.

Full size image

The model shows good qualitative agreement with the measurements presented in Fig. 2. For the same absorbed fluence, we observe a faster recovery when a smaller section of the waveguide is pumped. The effect of the length of the waveguide on the recovery becomes even more obvious when looking at the single wavelength transmission (dashed curves) instead of the convoluted wavelength transmission (solid curves). The recovery of T when a 3 μm spot is pumped is very steep whereas the recovery when the full 80 μm long waveguide is pumped is very shallow, even though the same free-carrier recombination time was used.

The rejection of modes due to bandshifting is independent of the waveguide length, while the absorption is not. That is, if both the long and short waveguides are pumped at the same fluence, resulting in identical carrier concentrations, light in the 80 μm long waveguide will experience ~27 times more absorption than light in the 3 μm waveguide. Consequently, the recovery in the shorter waveguide, at a single wavelength, will occur almost instantaneously once the mode becomes available (Fig. 4b dashed curves). In contrast, the recovery in the longer waveguide will be far slower (Fig. 4a dashed curves) and will largely be dictated by the carrier recombination times. Note that this difference in response between the two waveguides is somewhat mitigated when we consider a more realistic pulse with a 1 nm bandwidth (solid curves in Fig. 4). However, as expected, even for this more realistic case, the transmission of the shorter waveguide recovers much more rapidly than that of the longer waveguide. In the experiment, the free-carrier recombination time would probably be shorter for the smaller pump spot due to diffusion of free-carriers out of the pumped area14,36. Note that our model does not take this effect into account, hence an even faster recovery may be expected for the small pump spot than our model predicts.

Discussion

To conclude, we have demonstrated an ultrafast PhC based optical modulator that requires a footprint of only ~10 μm2, yet can operate over a broad range of wavelengths. The device uses bandshifting to shift the modegap and to enhance propagation losses by slowing down the light. Shortening the length of the modulator not only reduces the energy consumption, but surprisingly also allows for shorter modulation times and larger optical bandwidth operation. Our device shows a high degree of flexibility. Depending on the requirements, one can pick between modulation times as short as 95 ps, an extinction ratio as high as 10 dB or an optical bandwidth as large as 17 nm. These operating limits could most likely be improved with a careful design of the dispersion relation. As mentioned above, the dominant loss mechanism in our modulator is slow-light enhanced free-carrier absorption, which scales with ng. In the future, by combining a clever design of the bandstructure with an intentional increase in scattering losses, one can envision a modulator that relies on scattering losses which scale with (ref. 34), resulting in lower energy requirements (See Supplementary section Model and parameters).

Our silicon optical modulator compares favourably with those previously reported. It allows for much faster operation speed than is typical for devices using the thermo-optic effect ()5 and in particular of those that rely on thermo-optic bandshifting (~100 μs)37. Electro-absorption modulators using the quantum-confined Stark effect achieve faster operation speeds and lower energy consumption2,3, but require complex SiGe multilayers which are more difficult to fabricate and to integrate than silicon photonic crystal waveguides. Further, these electro-absorption modulators also suffer from higher insertion losses than photonic crystal waveguides. Both thermal and electro-absorption techniques require much larger footprints, as do Mach-Zehnder type modulators using carrier injection6. Modulators based on resonators such as Si microrings, can be achieved at a similar footprint12 but their optical bandwidths are usually in the ~100 pm range. Combining the techniques from electro-absorption modulators with our PhC design might lead to the best of both worlds, i.e. compact design with broad wavelength operation combined with faster modulation and lower power consumption. Also note that the recovery time of our device could be significantly reduced by sweeping out the carriers with the p-i-n junction. Furthermore, such a junction could also be used to electrically pump this device, thereby achieving full integration. Modulation bandwidths as high as 40 Gbit/s have been achieved with electrically pumped Si photonic crystal waveguides38. In all, this is a compact and simple to fabricate38 ultrafast optical modulator that joins other recent devices13,14,19,21,22,25,39,40,41,42,43 in the toolbox for optical interconnects, as we progress towards optical information processing.

Methods

Sample fabrication

The fabrication of the PhC waveguide starts with a SOITEC silicon-on-insulator wafer consisting of a 220 nm Si layer on top of a 2 μm SiO2 buffer layer. The required pattern is written in a layer of resist (ZEP520A) with an electron beam. The resist is developed using xylene with ultrasonic agitation44 after which the pattern is transferred to the Si membrane using Reactive Ion Etching with CHF3 and SF6 gases45. To obtain a freestanding membrane, the silica underneath the PhC area is removed using Hydrofluoric acid (the remaining area being protected by photoresist). The result is an 80 μm long and 220 nm thick Si PhC waveguide surrounded by air31. Note that our device was not optimized to reduce insertion losses in the wavelength range where we operate. By clever design of the transition region from the access waveguide to the PhC waveguide, the coupling efficiency can be as high as 95% for a group index range as wide as 200 (ref. 46 and Supplementary section Transmission spectra).

Pump-probe experiment

To pump the structure, a 100 fs pulse from a 810 nm, 80 MHz Ti:Sapphire oscillator laser is focussed on the PhC, either in an elliptical spot of approximately 3 by 200 μm (FWHMI) to cover the full length of the waveguide (80 μm), or in a circular spot of 3 μm (FWHMI) as shown in Fig. 1a. Using the transfer matrix method, we calculate that about 1.4% of the incident pump light is absorbed in the Si membrane. The transmission of the PhC waveguide in the telecom wavelength range (near 1550 nm) is probed by a 140 fs broadband pulse. To avoid nonlinear effects the intensity of the probe pulse is kept low. The time delay between the pump and the telecom probe pulse is varied by lengthening the path of the pump beam with a delay stage.