Abstract
Quantum entanglement plays an essential role in quantum information processing and quantum networks. One of the commonly-used methods to generate multiple entangled fields is to employ polarizing beam splitters. However, nonclassical input light fields are required and the generated entangled fields are always degenerate in such case. Here, we present a proof-of-principle demonstration of an efficient and convenient way to entangle multiple light fields via electromagnetically induced transparency (EIT) in an atomic ensemble. The atomic spin wave, produced through EIT in the Λ-type atomic system, can be described by a Bose operator and can act as an entangler. With such an entangler, any desired number of nondegenerate narrow-band continuous-variable entangled fields, in principle, can be generated through stimulated Raman scattering processes. This scheme holds great promise for applications in scalable quantum communication and quantum networks. PACS: 42.50.Gy, 03.67.Bg, 42.50.Dv, 42.65.Lm.
Similar content being viewed by others
Introduction
Quantum state exchange between light and matter is a basic component for quantum interface in quantum information processing. As is well known, light is the best long-distance quantum information carrier and the atomic ensembles can provide the promising tools for quantum information manipulation and storage. In facilitating quantum information processing and quantum networks, generations of light-light, atom-atom and atom-light multipartite entanglements play essential roles in the implementations of quantum information protocols1,2,3. So far, the majority studies on entanglement have dealt with the generations of multiple entangled light fields. Apart from the conventional way of generating multipartite entanglement by mixing squeezed fields created through parametric down-conversion processes in nonlinear optical crystals with linear optical elements, i.e., polarizing beam splitters (PBS)4,5,6,7 as entanglers, the atomic ensembles provide an alternative avenue to the generation of multi-entangled fields due to the virtue of narrow bandwidth, nondegenerate frequencies and long correlation time8,9,10,11,12,13,14. Based on the seminal proposal of Duan et al.8, the electromagnetically induced transparency15,16,17 (EIT)-based double-Λ-type atomic system has been actively implemented for efficiently creating nondegenerate entangled twin fields through either nondegenerate four-wave mixing (FWM) or Raman scattering processes9,10,11,12. The multicolor multipartite continuous-variable (CV) entanglement has also been achieved by using the multi-order coherent Raman scattering18 or multiple nondegenerate FWM processes13,14. Moreover, generations of entanglements between an atomic ensemble and light fields, as well as between two atomic ensembles, have also been realized8,19,20,21,22, which are vital for storage and processing of quantum information.
In this study, we propose an efficient and convenient scheme for quantum entangler via EIT in an atomic ensemble. The atomic spin wave, which can be described by a Bose operator and acts as the entangler, is produced through EIT in the Λ-type atomic configuration. Through stimulated Raman scattering processes, nondegenerate narrow-band multi-entangled fields up to any desired number can, in principle, be achieved via such an entangler. This proposed entangler is quite distinct as compared to the conventional PBS entangler23,24,25, since only coherent input light fields are needed for generating multipartite entanglement in the present scheme, whereas nonclassical input light fields are required when using the PBS entangler. Moreover, the present proposal is different from the previously proposed ones as given in Refs. 13, 14, 18. Here, the entanglement features between the atomic ensemble and the generated fields are investigated and it is shown that under the EIT condition the generated atomic spin wave can serve as an entangler. Also, this proposal is different from the one proposed in Ref. 8, since, in principle, any desired number of entangled fields can be produced through this entangler.
Results
Mechanism of excitations
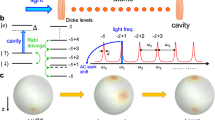
The considered model is shown in Fig. 1a, where energy levels |1〉, |2〉 and |3〉, forming the three-level Λ-type system, correspond, respectively, to the ground-state hyperfine levels 5S1/2 (F = 2), 5S1/2 (F = 3) and the excited state 5P1/2 in D1 line of the 85Rb atom with the ground-state hyperfine splitting of 3.036 GHz. A strong coupling field Ec (with frequency ωc and Rabi frequency Ωc) and a relatively weak probe field Ep (with frequency ωp and Rabi frequency Ωp) are tuned to be on resonance with the transitions |2〉–|3〉 and |1〉–|3〉, respectively. By applying a third mixing field Em1 (with frequency ωm1 and Rabi frequency Ωm1), off-resonantly coupled to levels |1〉 and |3〉, a Stokes field E1 can be created through the nondegenerate FWM process13,14. In fact, the produced Stokes field can be equivalently considered as a result of scattering the mixing field Em1 off the atomic spin wave (S) pre-established by the coupling and probe fields in the Λ-type EIT configuration formed by levels |1〉, |2〉 and |3〉, as shown in Fig. 1b, where the induced atomic spin wave acts as a frequency converter with frequency equal to the separation between the two lower states26,27. Subsequently, if more laser fields Em2, Em3, … EmN (with N being a positive integer) are applied to off-resonantly couple levels |1〉 and |3〉, more Stokes fields E2, E3, … EN can be produced through scattering the mixing fields off the same atomic spin wave. In what follows, we will investigate the entanglement features between the pre-established atomic spin wave and the generated Stokes fields.
(a) The Λ-type system of the D1 transitions in 85Rb atom coupled by the coupling (Ec), probe (Ep) and mixing (Em1, Em2, … EmN) fields and the corresponding Stokes fields (E1, E2, … EN) generated through multiple FWM processes. (b) The equivalent configuration of (a) with the two lower states driven by the atomic spin wave S pre-built by the strong on-resonant Ec and Ep fields in the Λ-type EIT configuration.
In this EIT-based configuration, we assume that the Rabi frequency of the scattering field is far smaller than its frequency detuning and the established atomic spin wave due to the on-resonant EIT is strong enough to ensure that different scattering fields have little influence on it. We also assume that the probe field is relatively weak as compared to the strong coupling field. Under these conditions, the collective atomic spin field S ( with Na being the total number of atoms in the interaction volume) can be viewed as approximately satisfying the bosonic commutation relation
with Na being the total number of atoms in the interaction volume) can be viewed as approximately satisfying the bosonic commutation relation  , so the produced atomic spin wave S can be treated as a bosonic field and the quantum state of the atomic ensemble can be transferred to that of the generated Stokes fields27.
, so the produced atomic spin wave S can be treated as a bosonic field and the quantum state of the atomic ensemble can be transferred to that of the generated Stokes fields27.
Generation of bipartite entanglement
We first investigate the bipartite entanglement between the atomic spin wave S and the generated Stokes field E1. As shown in Fig. 1b, we assume that the generated Stokes field is very weak as compared to the scattering field, thus, the scattering field is treated classically, whereas the Stokes field E1 and the atomic spin field S are treated quantum mechanically. After adiabatic elimination of the upper excited state, the effective Hamiltonian of this system in the interaction picture can be written as27

where a1 is the bosonic annihilation operator for the Stokes field E1 and  with Δ1 = ωm1 − ω31 being the detuning of the mixing field Em1 from the resonant transition |1〉–|3〉 and g23 being the coupling coefficient between the Stokes field and the respective atomic states. According to the realistic experimental parameters13,14, k1 is in the order of several cm−1; in such case, the estimated timescale for k1t = 1 corresponds to about tens of picoseconds. By solving the Heisenberg equations of motion for the operators S(t) and a1(t), one can get the solutions for the two operators as functions of their initial values:
with Δ1 = ωm1 − ω31 being the detuning of the mixing field Em1 from the resonant transition |1〉–|3〉 and g23 being the coupling coefficient between the Stokes field and the respective atomic states. According to the realistic experimental parameters13,14, k1 is in the order of several cm−1; in such case, the estimated timescale for k1t = 1 corresponds to about tens of picoseconds. By solving the Heisenberg equations of motion for the operators S(t) and a1(t), one can get the solutions for the two operators as functions of their initial values:


where a = cos2θ − sin2θ with tgθ = Ωp/Ωc. As seen in Fig. 1b, the collective atomic state is initially in a coherent superposition state and the Stokes field is initially in vacuum, so the initial state of the atom-field system can be written as  , where |1〉|0S〉 (|2〉|0s〉) represents an atom in state |1〉 (|2〉) and the Stokes field in vacuum. We use the criterion V = (Δu)2 + (Δν)2 < 4 proposed by Duan et al.28 to verify the bipartite entanglement between the atomic spin wave S and the generated Stokes field E1, where u = x1 − xS and ν = p1 + pS with
, where |1〉|0S〉 (|2〉|0s〉) represents an atom in state |1〉 (|2〉) and the Stokes field in vacuum. We use the criterion V = (Δu)2 + (Δν)2 < 4 proposed by Duan et al.28 to verify the bipartite entanglement between the atomic spin wave S and the generated Stokes field E1, where u = x1 − xS and ν = p1 + pS with  and
and  . Smaller the correlation V is, stronger the degree of the bipartite entanglement becomes.
. Smaller the correlation V is, stronger the degree of the bipartite entanglement becomes.
Figure 2 displays the interaction time evolutions of V under different ratios of Ωp/Ωc with k1 = 1. Obviously, it can be seen in Figs. 2a–2d that bipartite entanglement can be created as soon as when the interaction becomes nonzero; under different ratios of Ωp/Ωc, V, with the initial value of about 4, evolves with interaction time and becomes less than 4, which sufficiently indicates the generation of genuine bipartite entanglement between the Stokes field E1 and the atomic spin-wave field S. In addition, there exists a range of interaction time that V nearly approaches to zero, which means that the generated Stokes field is perfectly quantum correlated with the atomic spin wave. With an increase of the ratio Ωp/Ωc in a moderate range, the interaction time range for near-zero V values would decrease and the degree of bipartite entanglement becomes weakened.
The stimulated Raman scattering process described above for generating bipartite entanglement between the Stokes field E1 and the atomic spin-wave S has certain similar features as the parametric down-conversion process in a nonlinear crystal. The generated Stokes field E1 can be viewed as a result of frequency down-conversion process through mixing the scattering field Em1 with the atomic spin wave S pre-established by the coupling and probe fields. As the generation of a Stokes photon is always accompanied by an atomic spin-wave excitation, the down-converted frequency component (i.e., Stokes field) is strongly quantum correlated with the atomic spin wave; as a result, strong bipartite entanglement between the Stokes field and the atomic spin wave can be established. This idea can be generalized to the case with more laser fields Em2, Em3, … EmN tuned to the vicinity of the transition |1〉–|3〉 to mix with the same atomic spin wave, then all of the generated Stokes fields E1, E2, … EN would be entangled with the atomic spin wave and therefore entangled with each other. In such situation any desired number of entangled light fields, in principle, can be created with the atomic spin wave acting as an entangler. This proposed scheme can be further tested by applying another laser field Em2 scattering off the atomic spin wave to generate the tripartite entanglement.
Generation of tripartite entanglement
In the following, we consider the case of generating the Stokes fields E1 and E2 through scattering the laser fields Em1 and Em2 off the same atomic spin wave, respectively, as shown in Fig. 1b. The effective Hamiltonian of the system in the interaction picture has the form27

where  with Δ2 = ωm2 − ω31 being the frequency detuning of the mixing field Em2 from the transition |1〉–|3〉. In the similar way as calculating the bipartite entanglement generation, we solve the Heisenberg equations of motion for the operators S(t), a1(t) and a2(t) and the solutions for the three operators as functions of their initial values can be expressed as:
with Δ2 = ωm2 − ω31 being the frequency detuning of the mixing field Em2 from the transition |1〉–|3〉. In the similar way as calculating the bipartite entanglement generation, we solve the Heisenberg equations of motion for the operators S(t), a1(t) and a2(t) and the solutions for the three operators as functions of their initial values can be expressed as:



where  . We demonstrate the tripartite entanglements of the generated Stokes fields E1, E2 and atomic spin wave S by employing the criterion proposed by van Lock-Furusawa (VLF)6,7 with inequalities as follows:
. We demonstrate the tripartite entanglements of the generated Stokes fields E1, E2 and atomic spin wave S by employing the criterion proposed by van Lock-Furusawa (VLF)6,7 with inequalities as follows:



where  and gi (i = 1,2,3) are arbitrary real numbers. In a similar way as that used in Ref. 29, we set
and gi (i = 1,2,3) are arbitrary real numbers. In a similar way as that used in Ref. 29, we set  ,
,  and
and  . Satisfying any pair of these three inequalities is a sufficient condition of realizing the tripartite entanglement and also smaller the correlations V12, V1s and V2s are, higher the degree of tripartite entanglement will be.
. Satisfying any pair of these three inequalities is a sufficient condition of realizing the tripartite entanglement and also smaller the correlations V12, V1s and V2s are, higher the degree of tripartite entanglement will be.
Figures 3a–3d depict the evolutions of the VLF correlations as a function of interaction time with k1 = 1 and Ωp/Ωc = 1/20 under different k2 values. It can be seen that when k2 is far smaller than k1 (see Fig. 3a), there only exists a very limited range of the interaction time within which the inequalities for V12 and V2s are fulfilled, whereas V1s with the minimal value nearly to zero is smaller than 4 in a wide range of the interaction time; this means that strong entanglement between the generated Stokes field E1 and the atomic spin wave is obtained, whereas the generated Stokes field E2 is weakly entangled with both the Stokes field E1 and atomic spin wave S. With an increase of k2, the minimal values of V12 and V2s would decrease and the ranges of interaction time with both V12 and V2s being smaller than 4 would increase, whereas V1s displays an opposite behavior, that is, the degree of bipartite entanglement between the generated Stokes field E1 and atomic spin wave is weakened and that between the Stokes field E2 and Stokes field E1 (or atomic spin wave) is strengthened. When k1 = k2 = 1 (see Fig. 3c), V12, approaching to 2 after certain interaction time, is smaller than 4 over the entire interaction time range and there exists a broad range of interaction time within which the inequalities for V12, V1s and V2s are all satisfied. In this case, the Stokes fields E1 and E2 and the atomic spin wave S are CV entangled with each other and the strongest tripartite entanglement is obtained. Further increasing k2 would enhance the degree of bipartite entanglement between the Stokes field E2 and atomic spin wave and degrade the entanglement between the Stokes field E1 and Stokes field E2 (or atomic spin wave). In principle, this scheme can be generalized to generate any desired number of maximally-entangled fields by using the atomic spin wave as an entangler through applying more laser fields Em3, Em4, … EmN tuned to the vicinity of the transition |1〉–|3〉 under the condition of k1 = k2 = k3 … = kN. Detailed calculations show that the VLF correlations V12, V1s and V2s exhibit weak dependence on the variation of ratio Ωp/Ωc, as long as the probe field is relatively weak as compared to the coupling field.
Discussion
In the above EIT-based configuration, the Rabi frequencies of the scattering fields should be small as compared to their frequency detunings so that coupling between different scattering fields can be neglected and the atomic spin wave should be strong enough to ensure that different scattering fields have little influence on it, which can be realized by using substantially strong probe and coupling fields as compared to the scattering fields. Moreover, the probe field should be relatively weak as compared to the coupling field, so that the produced atomic spin wave S can be treated as a bosonic field. In an atomic medium, there will be realistic imperfections, such as finite coherence times, atomic diffusion and Doppler broadening. In the above analysis, we did not take into account these effects, so that the main physics in such system can be resolved and better understood. The influences to entanglement due to those realistic imperfections will be analyzed in the future work by using a Heisenberg-Langevin approach.
It should be noted that the present scheme is different from the one proposed by Duan et al.8. In the current scheme, the atomic spin wave is created in advance via EIT, which acts as an entangler and provides a way to generate nondegenerate multiple CV-entangled fields to any desired number. In addition, in Ref. 8, the atomic spin wave is produced through spontaneous Raman scattering, so the generated Stokes or anti-Stokes field would emit in all directions and the photon production efficiency is very low, whereas in the present scheme, the generated Stokes field propagates along a particular direction determined by the phase-matching condition for FWM13,14, so the photon production efficiency is much higher, which would bring great facility in realistic quantum information processing protocols. Moreover, the present scheme is different from our previous proposal14. In the present EIT-based configuration, we assume that the probe field is relatively weak as compared to the strong coupling field, so the produced atomic spin wave S can be treated as a bosonic field and serve as an entangler and the quantum state of the atomic ensemble can be transferred to that of the generated Stokes field. Also, the generated anti-Stokes fields are relatively weak as compared to the Stokes fields, so the entanglement properties between the Stokes and anti-Stokes fields do not need to be taken into account. However, as discussed in Refs. 13, 14, strong coupling and probe fields with nearly equal Rabi frequencies are employed in the previous scheme in order to enhance the production efficiencies of both the Stokes and anti-Stokes fields and promote entanglement between them.
Note also that, as compared to the routinely-employed method to produce multi-field entanglement by using PBS entanglers4,5,6,7, where the interferometric stabilization of the optical paths is required and the entangled multi-fields are degenerate and suffer from short correlation time (~ps), the present scheme can be employed to generate narrow-band multicolor entangled CV fields with a long correlation time (~ms or even ~s30,31) by using a single entangler, where the correlation time is determined by the coherence decay time between the two lower atomic states due to the finite interaction time between atoms and light fields. Furthermore, the proposed entangler is different from and superior to the PBS entangler23,24,25 in that the generation of multipartite entanglement using PBS entanglers is a linear process, whereas it is a nonlinear one for the present entangler, so as nonclassical input light fields are required for using PBS entanglers to generate multipartite entanglement, only coherent input light fields are needed for using the present entangler to create multipartite entanglement, which will greatly simplify its practical implementation.
In conclusion, we have proposed an efficient and convenient scheme for realizing an entangler from an EIT-based atomic ensemble. The entangler has the virtue of being able to generate, in principle, arbitrary number of nondegenerate and narrow-band CV-entangled fields with a long correlation time, which can satisfy all the essential requirements for constructing a scalable quantum repeater for the realization of long-distance quantum communication. In addition, only coherent input light fields are required for generating multipartite entanglement. Together with the entanglement generations between two atomic ensembles and entanglement swapping8,19,20,21,22, light-light, atom-atom and atom-light multipartite entanglements can be achieved, which will find promising applications in quantum information processing and quantum networks.
Methods
Calculation of time-dependent operators
According to the Heisenberg equation of motion  , one can get the solutions for the field operators as functions of their initial values by substituting the effective Hamiltonian HI into the equations of motion. We assume that the atomic spin wave is strong enough, so different scattering fields will have little influence on it. We also assume that the generated Stokes fields are very weak as compared to the corresponding scattering fields, so the approximations of undepleted coupling and probe fields as well as scattering fields can be employed in the above calculations. Similar hyperbolic solutions for generating tripartite entanglement by applying cascaded or concurrent nonlinearities have been examined by Olsen et al.29.
, one can get the solutions for the field operators as functions of their initial values by substituting the effective Hamiltonian HI into the equations of motion. We assume that the atomic spin wave is strong enough, so different scattering fields will have little influence on it. We also assume that the generated Stokes fields are very weak as compared to the corresponding scattering fields, so the approximations of undepleted coupling and probe fields as well as scattering fields can be employed in the above calculations. Similar hyperbolic solutions for generating tripartite entanglement by applying cascaded or concurrent nonlinearities have been examined by Olsen et al.29.
References
Bouweester, D., Ekert, A. & Zeilinger, A. The Physics of Quantum Information (Springer-Verlag, Berlin, 2000).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge University Press, Cambridge, 2000).
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001).
Aoki, T. et al. Experimental creation of a fully inseparable tripartite continuous-variable state. Phys. Rev. Lett. 91, 080404 (2003).
van Loock, P. & Braunstein, S. L. Multipartite entanglement for continuous variables: A quantum teleportation network. Phys. Rev. Lett. 84, 3482–3485 (2000).
van Loock, P. & Furusawa, A. Detecting genuine multipartite continuous-variable entanglement. Phys. Rev. A 67, 052315 (2003).
Duan, L. M., Lukin, M. D., Cirac, J. I. & Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001).
van der Wal, C. H. et al. Atomic memory for correlated photon states. Science 301, 196–200 (2003).
Kuzmich, A. et al. Generation of nonclassical photon pairs for scalable quantum communication with atomic ensembles. Nature 423, 731–734 (2003).
Balic, V., Braje, D. A., Kolchin, P., Yin, G. Y. & Harris, S. E. Generation of paired photons with controllable waveforms. Phys. Rev. Lett. 94, 183601 (2005).
Boyer, V., Marino, A. M., Pooser, R. C. & Lett, P. D. Entangled images from four-wave mixing. Science 321, 544–547 (2008).
Yang, X. H., Sheng, J. T., Khadka, U. & Xiao, M. Generation of correlated and anticorrelated multiple fields via atomic spin coherence. Phys. Rev. A 85, 013824 (2012).
Yang, X. H., Zhou, Y. Y. & Xiao, M. Generation of multipartite continuous- variable entanglement via atomic spin wave. Phys. Rev. A 85, 052307 (2012).
Harris, S. E. Electromagnetically induced transparency. Phys. Today 50, 36–42 (1997).
Xiao, M., Li, Y. Q., Jin, S. Z. & Gea-Banacloche, J. Measurement of dispersive properties of electromagnetically induced transparency in rubidium atoms. Phys. Rev. Lett. 74, 666–669 (1995).
Fleischhauer, M., Imamoglu, A. & Marangos, J. P. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 77, 633–673 (2005).
Kien, F. L., Patnaik, A. K. & Hakuta, K. Multiorder coherent Raman scattering of a quantum probe field. Phys. Rev. A 68, 063803 (2003).
Duan, L. M., Cirac, J. I., Zoller, P. & Polzik, E. S. Quantum communication between atomic ensembles using coherent light. Phys. Rev. Lett. 85, 5643–5646 (2000).
Julsgaard, B., Kozhekin, A. & Polzik, E. S. Experimental long-lived entanglement of two macro- scopic objects. Nature 413, 400–403 (2001).
Yuan, Z. S. et al. Experimental demonstration of a BDCZ quantum repeater node. Nature 454, 1098-1101 (2008).
Sangouard, N., Simon, C., de Riedmatten, H. & Gisin N. Quantum repeaters based on atomic ensembles and linear optics. Rev. Mod. Phys. 83, 33-80 (2011).
Kim, M. S., Son, W., Bužek, V. & Knight, P. L. Entanglement by a beam splitter: Nonclassicality as a prerequisite for entanglement. Phys. Rev. A 65, 032323 (2002).
Wang, X. B. Theorem for the beam-splitter entangler. Phys. Rev. A 66, 024303 (2002).
Feng, X. L., Li, R. X. & Xu, Z. Z. Beam splitter entangler for light fields. Phys. Rev. A 71, 032335 (2005).
Merriam, A. J. et al. Efficient nonlinear frequency conversion in an all-resonant double-Λ system. Phys. Rev. Lett. 84, 5308–5311 (2000).
Ou, Z. Y. Efficient conversion between photons and between photon and atom by stimulated emission. Phys. Rev. A 78, 023819 (2008).
Duan, L. M., Giedke, G., Cirac, J. I. & Zoller, P. Inseparability criterion for continuous variable systems. Phys. Rev. Lett. 84, 2722–2725 (2000).
Olsen, M. K. & Bradley, A. S. Asymmetric polychromatic tripartite entanglement from interlinked χ(2) parametric interactions. Phys. Rev. A 74, 063809 (2006).
Zhang, R., Garner, S. & Hau, L. V. Creation of long-term coherent optical memory via controlled nonlinear interactions in Bose-Einstein condensates. Phys. Rev. Lett. 103, 233602 (2009).
Schnorrberger, U. et al. Electromagnetically induced transparency and light storage in an atomic mott insulator. Phys. Rev. Lett. 103, 033003 (2009).
Acknowledgements
This work is supported by NBRPC (Nos. 2012CB921804 and 2011CBA00205), the National Natural Science Foundation of China (Nos. 11274225, 10974132, 50932003 and 11021403) and Innovation Program of Shanghai Municipal Education Commission (No. 10YZ10). Yang's e-mail is yangxihua@yahoo.com or yangxih@yahoo.com.cn; M. Xiao's e-mail is mxiao@uark.edu.
Author information
Authors and Affiliations
Contributions
X.Y. and M.X. conceived the idea for this project. X.Y. and Y.Z. performed the calculations and prepared figures 1–3. X.Y. and M.X. wrote the main manuscript text. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Yang, X., Zhou, Y. & Xiao, M. Entangler via electromagnetically induced transparency with an atomic ensemble. Sci Rep 3, 3479 (2013). https://doi.org/10.1038/srep03479
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03479
This article is cited by
-
Deterministically Entangling Two Remote Atomic Ensembles via Light-Atom Mixed Entanglement Swapping
Scientific Reports (2016)
-
Electromagnetically Induced Entanglement
Scientific Reports (2015)
-
Dephasing-Induced Control of Interference Nature in Three-Level Electromagnetically Induced Tansparency Systems
Scientific Reports (2015)
-
A universal quantum information processor for scalable quantum communication and networks
Scientific Reports (2014)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.