Abstract
Spin switching of organometallic complexes by ferromagnetic surfaces is an important topic in the area of molecular nanospintronics. Moreover, graphene has been shown as a 2D surface for physisorption of molecular magnets and strain engineering on graphene can tune the spin state of an iron porphyrin (FeP) molecule from S = 1 to S = 2. Our ab initio density functional calculations suggest that a pristine graphene layer placed between a Ni(111) surface and FeP yields an extremely weak exchange interaction between FeP and Ni whereas the introduction of defects in graphene shows a variety of ferromagnetic and antiferromagnetic exchange interactions. Moreover, these defects control the easy axes of magnetization, strengths of magnetic anisotropy energies and spin-dipolar contributions. Our study suggests a new way of manipulating molecular magnetism by defects in graphene and hence has the potential to be explored in designing spin qubits to realize logic operations in molecular nanospintronics.
Similar content being viewed by others
Introduction
The combination of spintronics and molecular electronics is a rapidly emerging research field due to the possibility of manipulating spin and charge degrees of freedom at the molecular scale. A key factor in molecular nanospintronics is the efficient control of electronic and magnetic properties of molecules acting as the active region of spin-dependent electronic transport. Metalorganics with a magnetic centre own a key position in this respect. The possibility of controlled spin manipulation1,2,3,4 makes these magnets attractive for several device applications including spin-dependent electronics, molecular switches etc. In this regard, the use of materials that could be stabilized at an ultra thin atomic limit are a perfect choice for future devices, where graphene has already made its mark very significantly. Very recently, we have proposed5 that strain engineering in a graphene lattice carrying a divacancy defect can switch the spin state of an iron porphyrin (FeP) molecule adsorbed on the defect site from S = 1 to S = 2 in a reversible way.
Graphene has been very much in the center of research interest in the last decade6,7,8 and continues to be there as a potential key-material in electronics, storage materials, bio-sensors, DNA-sequencing, drug delivery and so on. It has also been proven promising in the area of bio-molecular devices. Free standing graphene with sp2 bonded C atoms possess no magnetism but it can be introduced by either confinement9, where unsaturated bond or electron localization plays the key role, or depositing on a magnetic surface10, where substrate induced moment is observed. It should be noted that graphene is prone to several types of point defects, e.g., vacancies, Stone-Wales defects etc11,12. The influence of these defects in the induced magnetism in graphene is less explored in the literature, which may have important consequences in mediating exchange interactions via graphene. In this article, our objective is to explore magnetism in graphene adsorbed on a Ni(111) surface and utilize the possibility to achieve a control over magnetic interaction between Ni surface and organometallic molecule like iron porphyrin (FeP). The first part of our discussion thus will be devoted to magnetism in graphene including the effect of defects in the graphene lattice and in the later part we shall discuss magnetic interactions between FeP and magnetic Ni surface via graphene.
It has been shown that a magnetic surface with partially filled d-orbital favors chemisorption of molecular magnets4. Due to the formation of covalent bonds with the magnetic substrates, FeP is structurally deformed with enhanced Fe-N bond lengths compared to the gas-phase geometry, leading to a change in the spin state of Fe from the gas-phase value of S = 1 to a high spin-state S = 2 for the chemisorbed situation4. However, the presence of adsorbed graphene between FeP and magnetic substrates weakens both chemical and magnetic interaction due to physisorption of FeP on graphene. More importantly, as will be evidenced later, ferrimagnetism induced in graphene by the underlying Ni substrate in a peculiar sub-lattice pattern dictates the nature and strength of magnetic interaction between FeP and the Ni substrate whereas a free standing non-magnetic graphene or graphene deposited on non-magnetic substrates, such as Cu, Pt etc. acts inert in this respect. A complex scenario occurs in the presence of defects in graphene as this changes the induced magnetisation profile in the graphene lattice and hence the nature and strength of magnetic interaction. The primary focus of our study is the role of defects viz. monovacancy, divacancy and Stone-Wales (SW) defects in manipulating intramolecular magnetism as well as molecule-substrate interactions. It should be stated that controlled introduction of defects in graphene has been realised recently13,14, which, as we demonstrate here by first principles density functional calculations, opens up the possibility to manipulate magnetic interactions via these defects.
Results
Induced magnetism in pure and defected grapheme
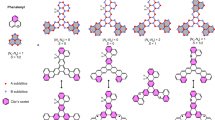
A sp2 -bonded graphene lattice has three in-plane saturated bonds along with an out-of-plane π-bond. The dispersive π-bonding (anti bonding) band appears just below (above) the Fermi energy. Once adsorbed on a hexagonal facet of Ni(111) surface, C atoms in one of the two sublattices make direct bonds with Ni atoms right underneath them, while the other sublattice C atoms stay hanging on the hexagonal centres of the top Ni layer. From now on, we indicate the C-atom, that makes direct bond with Ni, as CA and the other sublattice C atoms as CB. The calculated distance between the graphene layer and the Ni surface comes out to be 2.1 Å for defect free graphene, which agrees quite well with previous experimental10 and theoretical15 studies. Owing to the strong covalent interaction between  and CA -pz orbitals, the C-pz orbital is pushed down in energy, thus allowing the CA sublattice to hybridize with the lower part of the Ni band in both majority and minority spin channels. The C-pz orbital of the other sublattice of graphene interacts weakly with
and CA -pz orbitals, the C-pz orbital is pushed down in energy, thus allowing the CA sublattice to hybridize with the lower part of the Ni band in both majority and minority spin channels. The C-pz orbital of the other sublattice of graphene interacts weakly with  orbital through π-bonding and appears more close to the Fermi energy. A CA atom gains a small moment of 0.018 μB with an opposite polarization compared to the Ni moment in the process of strong hybridization while a CB atom acquires a comparatively larger moment of 0.029 μB with the same sign as the Ni moment. Hence, the whole graphene layer acquires the characteristic of a ferrimagnet with alternative sublattices having opposite spin polarizations as shown in Fig. 1(a). The total contribution in the defect-free graphene arising from CB (36 atoms) is 1.025 μB and from CA (36 atoms) is −0.651 μB where each C atom of a particular sublattice contributes equally. Due to these features of hybridization, the broad surface Ni band also gets divided into two sub-bands, of which one appear 2–4 eV below Fermi energy and the other appears close to Fermi energy (discussed below).
orbital through π-bonding and appears more close to the Fermi energy. A CA atom gains a small moment of 0.018 μB with an opposite polarization compared to the Ni moment in the process of strong hybridization while a CB atom acquires a comparatively larger moment of 0.029 μB with the same sign as the Ni moment. Hence, the whole graphene layer acquires the characteristic of a ferrimagnet with alternative sublattices having opposite spin polarizations as shown in Fig. 1(a). The total contribution in the defect-free graphene arising from CB (36 atoms) is 1.025 μB and from CA (36 atoms) is −0.651 μB where each C atom of a particular sublattice contributes equally. Due to these features of hybridization, the broad surface Ni band also gets divided into two sub-bands, of which one appear 2–4 eV below Fermi energy and the other appears close to Fermi energy (discussed below).
Intricate magnetization profiles in the graphene lattice are observed with the introduction of lattice defects, as shown in Figs. 1(b)–(d). We have considered three types of defects, that are abundant in graphene, e.g. the monovacancy, where one CA atom is removed, a divacancy, where a pair of CA and CB atoms are removed and Stone-Wales defect, where a C-bond is rotated by 90° to form a 5-5-7-7 structure. The following structural and magnetic changes are observed: (i) monovacancy: the graphene lattice with a monovacancy is magnetised almost in a similar fashion as the pristine graphene. Only at the defect site, the absence of one CA atom (with moment of opposite polarization to Ni in the ideal honeycomb lattice) reduces the moments of the surrounding three CB atoms to 0.016 μB as shown in Fig. 1(b); (ii) divacancy: to heal a divacancy defect in graphene, one Ni atom is lifted up towards the vacancy center leaving a void in the surface Ni layer as shown in the inset of Fig. 2. Due to the modified coordination and thus modified hybridization and ligand field, the spin moment of that particular Ni atom quenches to 0.04 μB. This local structural deformation is transmitted through the whole unit cell and hence, the induced moments in different C-atoms vary significantly due to strongly affected graphene-Ni interaction (Fig. 1(c)). This results in a decrease in total induced moments in both C-sublattices, amounting to 0.403 μB(35 atoms) and −0.165 μB(35 atoms); (iii) SW: compared to a divacancy defect, a SW defect center introduces more structural changes by mostly buckling the graphene lattice. The effective separation between the graphene layer and the Ni surface varies significantly in the unit cell (2.1 Å to 2.6 Å) for this defect and hence the induced magnetization in graphene varies from 0.003 to 0.03 μB. The sublattice magnetization profile shown in Fig. 1(d) depicts the situation with the differently polarized moments in the graphene lattice being 0.35 μB(39 atoms) and −0.17 μB(33 atoms). The buckling in the graphene lattice affects the C-Ni hybridisation, which has a direct impact on varying the magnetization on different C atoms. Therefore, one may conclude that the controlled introduction of specific lattice defects is a possible route to drastically modify the magnetization profile of the adsorbed graphene lattice on Ni.
Spin-polarized d-orbital projected density of states of Fe in FeP and the Ni atom occupying the divacancy site shown in the right panel for (left) graphene without defect and (right) graphene with a divacancy defect.
The corresponding geometries with FeP/graphene/Ni are shown in the inset. The vertical bars indicate  character of Fe and Ni at different energy positions in the DOS.
character of Fe and Ni at different energy positions in the DOS.
Interaction between FeP and pristine grapheme
As mentioned earlier, a metallic magnetic surface promotes chemisorption of an organometallic molecule (FeP)4 and hence a strong exchange interaction between Fe and the magnetic substrate. It would be desirable to be able to control this exchange interaction. We show here that a graphene layer placed between the magnetic surface and FeP blocks the path for strong exchange interaction between the magnetic molecule and the Ni substrate and at the same time the ferrimagnetic graphene opens up new paths of magnetic interaction between the magnetic center in the molecule and the magnetic surface.
The composite system, which we consider is FeP adsorbed on a graphene layer deposited on a Ni(111) surface. FeP becomes physisorbed on the crystalline graphene lattice or at defect centres in the graphene lattice. The average distance between FeP and graphene is calculated to be 3.1 Å and the graphene to Ni distance turns out to be 2.1 Å. Hence, the magnetic interaction with an effective distance of 5.2 Å is expected be an order or two weaker compared to the chemisorbed situation (without graphene) if only direct exchange is considered. From our calculations, we confirm this scenario where the variation in strength of the exchange energy enters due to different adsorption sites.
We now consider each adsorption site individually. We have considered three adsorption sites for pristine graphene, namely Top-A, Top-B and Hexagon positions, where the Fe centre of FeP is on top of CA, CB and in the center of a hexagonal ring, respectively. The magnetization profile for a defect free graphene layer has an alternative arrangement of oppositely polarized moments of the C bipartite lattice. The Fe atom of FeP placed on top of a hexagonal site has a vanishingly small exchange coupling with the Ni substrate whereas the binding energy (2.22 eV) is the highest for this adsorption site. The spin-state of Fe changes from the value of the free molecule, S = 1 to S = 2 for this most favorable adsorption site. A strong π-π stacking between the ring atoms of FeP and the π network in the graphene lattice gives rise to enhanced Fe-N bond lengths along with an overall outward expansion of FeP. Hence, a change of spin state occurs and the high spin state is stabilized.
Adsorption of FeP directly on the Ni surface leads to the formation of chemical bonds between FeP and Ni and hence establishes a fairly strong ferromagnetic exchange coupling between them4. The insertion of the graphene layer blocks the direct exchange between Fe and Ni significantly causing the magnetic coupling to be mediated in an indirect way. The local ligand field on Fe, predominantly provided by N atoms along with weaker contribution from the C-ring, affects the energy positions of the Fe-d orbitals. In-plane N-px and py orbitals hybridize strongly with  and push this level up in energy. The out-of-plane orbitals on N atoms provide a π-type bond with Fe-dπ orbital and hence push the dπ orbital above the dxy orbital. We note in passing that the ligand field effects discussed here are influenced by the formation of molecular orbital states within the FeP molecule, which are influenced by the interaction with the graphene layer. Hence, these effects are different from the crystal field level splitting in a square planar point charge arrangement. Along with the π − π interaction between Fe-d and N-p, C-p and N-p orbitals contribute to intramolecular hybridization in FeP. However, a much weaker hybridization is observed between FeP and graphene.
and push this level up in energy. The out-of-plane orbitals on N atoms provide a π-type bond with Fe-dπ orbital and hence push the dπ orbital above the dxy orbital. We note in passing that the ligand field effects discussed here are influenced by the formation of molecular orbital states within the FeP molecule, which are influenced by the interaction with the graphene layer. Hence, these effects are different from the crystal field level splitting in a square planar point charge arrangement. Along with the π − π interaction between Fe-d and N-p, C-p and N-p orbitals contribute to intramolecular hybridization in FeP. However, a much weaker hybridization is observed between FeP and graphene.
For the Top-A position, the Fe moment is antiparallel to the moment of CA (−0.018 μB) and hence is parallel to the Ni moment, giving rise to a ferromagnetic exchange coupling of strength ~1.8 meV between FeP and Ni. For the Top-B site, an antiferromagnetic exchange coupling (7 meV) between Fe and Ni is observed. Similar to the Top-A site, the spin-state of Fe is retained as S = 1. The binding energies of FeP on Top-A and Top-B sites are only 2 meV and 17 meV higher than the most favorable Hexagonal site, where a vanishingly small exchange coupling is observed.
Influence of defects
Now we discuss the role of defects in modifying the structural, electronic and magnetic properties. (i) On a monovacancy defect, Fe prefers to sit on top of the defect site giving rise to a ferromagnetic coupling energy of 7 meV between Fe and Ni. The spin state remains unaffected with S = 1. (ii) The situation differs quite significantly for a divacancy defect. One Ni atom from the substrate occupies the divacancy site and makes a strong chemical bond with Fe in FeP as shown in the inset of Fig. 2. As a result, the Fe atom is pulled towards the Ni atom from the plane of FeP stretching the Fe-N bond lengths. This changes the spin state from S = 1 to S = 2 as was observed in a similar situation in an earlier work5. An antiferromagnetic coupling (energy of 22 meV) between Fe and Ni is observed in this case. (iii) Finally, a SW defect causes an antiferromagnetic exchange interaction of strength ~14.8 meV between Fe and Ni. In this case, the spin state of Fe is retained as S = 1.
Due to complex structural changes, the electronic structures of Fe and Ni are expected to be modified significantly depending on the adsorption site. To make a comparison, we show in Fig. 2 the d-projected DOS of Fe in FeP and one of the selected Ni atoms of the Ni substrate for two cases: (a) Fe placed at the hexagonal site and (b) Fe placed on top of a divacancy site. For the hexagonal adsorption site, the d-DOS of Fe is very close to a S = 2 DOS of Fe in a gas-phase FeP molecule, indicating a very weak effect on the Fe DOS due to the presence of graphene and Ni. To elucidate this clearly, we have indicated the  dominated peaks in the Fe and Ni DOS, which do not display any significant hybridization between these states (Fig. 2). This is demonstrated by the absence of common features of the Fe and Ni projected states. On the contrary, for a divacancy site, Fe and Ni DOS are significantly modified with the presence of clearly hybridizing
dominated peaks in the Fe and Ni DOS, which do not display any significant hybridization between these states (Fig. 2). This is demonstrated by the absence of common features of the Fe and Ni projected states. On the contrary, for a divacancy site, Fe and Ni DOS are significantly modified with the presence of clearly hybridizing  states indicated by bars in Fig. 2, that coincide in energy. Also, one clearly observes localized d-states of the Ni atom surrounded by C atoms. As a result of the strong p-d hybridization between Ni and C states, the local magnetic moment of these Ni atoms is almost quenched. In this case, a direct bonding controls the exchange mechanism and FeP is antiferromagnetically coupled to Ni with a coupling strength of 22 meV.
states indicated by bars in Fig. 2, that coincide in energy. Also, one clearly observes localized d-states of the Ni atom surrounded by C atoms. As a result of the strong p-d hybridization between Ni and C states, the local magnetic moment of these Ni atoms is almost quenched. In this case, a direct bonding controls the exchange mechanism and FeP is antiferromagnetically coupled to Ni with a coupling strength of 22 meV.
We can now think of a situation where a graphene lattice grown on Ni possesses several types of defects, e.g., monovacancy, divacancy and SW. It should be noted that the defect formation energies (DFE) in free-standing graphene are much higher than for the situation of graphene deposited on a Ni(111) surface. Our calculated values of the DFE are 2.91 eV and 3.83 eV for a monovacancy and a divacancy defect in comparison to 7–8 eV for vacancy formation energies in a free-standing graphene. Therefore, the creation of these defects, either naturally or by an ion-irradiation experiment should be easier compared to free standing graphene. Molecules adsorbed on graphene with these defects introduced, are expected to produce different kinds of exchange coupling depending on specific defect sites.
Due to the presence of defects in graphene and the adsorbed FeP, the magnetic properties of the first Ni layer also change in a very interesting way. In Fig. 3, we show the change in the magnetic moments of the Ni atoms in the first layer when defects are present along with FeP, compared to the case with a pure graphene layer on the Ni substrate (indicated as m0) as a function of the coordination shells around the region of the first layer where defects are present. For a pure graphene lattice deposited on Ni, the magnetic moments in the first Ni layers have a homogeneous pattern throughout the layer. In addition to that, the effect of adsorbed FeP on the first layer Ni moment is shown for the Top-A position, where a small modification of the moment is observed. However the most noticeable changes are seen in presence of defected graphene, where different types of non-monotonic variations depending on the type of defect are found. For example, the Ni atoms closest (in the first coordination shell) to monovacancy center lose around 0.15 μB whereas for distant shells, the moments increase by a smaller amount (~0.025 μB). The most interesting change is observed for the SW defect. In the first coordination shell, the Ni atoms lose around 0.075 μB whereas for the fifth shell, a large increase of about 0.2 μB is observed. Moreover, a gradual change in the moment is observed as a function of coordination shells with a changeover in sign in the third shell. It is observed that a SW defect causes a significant buckling in the graphene lattice and as a result, the distance between the buckled graphene sheet and the first Ni layer has a significant spatial variation, which leads to the variation in the local Ni moments. Therefore, one may conclude that the modifications of the first layer Ni moments affect the exchange interaction between Ni and Fe in FeP in different ways for different types of defects.
Change in magnetic moments of Ni atoms in the first layer (averaged over moments in the respective coordination shells) between FeP/graphene/Ni with different types of defects as indicated and graphene/Ni without FeP and any defect in the graphene layer (moment indicated as m0).
The coordination shells are chosen around the defect centers above which the molecules are adsorbed. The first coordination shell includes the nearest neighbor atoms in a hexagonal cell (of Ni (111) surface). 2nd coordination shell consists of next nearest neighbors and so on. Atoms in the unit cell are considered only. An average moment in the respective coordination shell is shown. The shells are indicated in the x-axis label. Also, the optimized structure (side) of graphene with a SW defect on Ni is shown with an area zoomed around SW site. In the zoomed area, both graphene lattice with SW center (5577) and first layer of Ni surface are shown.
The next important question is whether the FeP molecules will overcome possible energy barriers, once adsorbed on graphene, so that they move to different adsorption sites with comparable energies. In order to investigate this, we have performed nudged elastic band (NEB) calculations to determine the energy barrier in moving an FeP molecule between a hexagonal site to a Top-A site on a defect free graphene lattice. We have chosen the Top-A site as it is only 2 meV higher in energy than the hexagonal site. A defect-free graphene is intentionally chosen as the adsorption on a defected graphene is expected to be stronger5,16,17 and hence, the transition barrier is expected to be higher. Therefore our calculated value for a defect-free graphene sets the lower limit for the diffusion barrier. The calculated energy barrier is 33 meV as observed in Fig. 4. This indicates that FeP can diffuse from the hexagonal ground state adsorption site to the next energetically available Top-A site at the room temperature or slightly above it. However, one can control this diffusion by adjusting the temperature. In Fig. 4, the geometries of FeP and a part of the underlying graphene lattice are presented along the reaction path. One may conclude that FeP molecules will remain locked due to the energy barrier, at their respective adsorption sites with well-defined spin states and exchange coupling with underlying Ni substrate. One may envisage controlled formation of specific types of defects and achieving either parallel or antiparallel orientation of Fe moments relative to the moments in the Ni layers.
We should point out that one may reach metastable solutions for these systems. Therefore, we have considered several starting possibilities (both in structure and spin state) for each adsorption geometry to reach the true ground state. Most importantly, spin switching (S = 1 to S = 2) has been observed for FeP adsorbed on the Hexagonal and divacancy adsorption sites. On the divacancy site, a high spin S = 2 solution is always obtained. S = 1 and S = 2 spin states are very close in energy for the Hexagonal and SW sites. For SW, an AFM ground state is found with S = 1 while a FM S = 2 spin state is 6 meV higher in energy. For the Hexagonal site, S = 2 spin state is found to be the ground state with degenerate FM and AFM solutions. However, a S = 1 spin state could be stabilized at 24 meV higher energy. For other adsorptions sites, a stable S = 1 spin state is always found.
Magnetic anisotropy and spin dipole moment
So far, organometallic complexes have been successfully deposited18 on nonmagnetic (e.g., Cu, Au, Ag etc.) and magnetic surfaces (e.g., Co, Ni etc.). The magnetic ordering between the molecular spins has been realized either by exchange coupling with the magnetic substrates or by externally applied magnetic field. As thermal fluctuations are always detrimental towards the magnetic ordering, the strength of molecular magnetic anisotropy stands as an important issue. In organic molecules with a transition metal atom center, the ligand field splitting is 2–3 order larger compared to the spin-orbit coupling. A perturbative approach thus can safely be considered to calculate the magnetocrystalline anisotropy energy. The leading contribution comes from the second order term while higher order terms can be neglected.
The magnetocrystalline anisotropy originates from coupling between lattice and spin, which can be expressed as:

where HSO is the spin-orbit coupling hamiltonian and ζ is the spin orbit coupling constant defined as  , R3d(r) being the radial part of the 3d wave function. The value of ζ for Fe2+ has been considered as 0.049 eV19, taken from the literature. Spin-orbit contribution to the energy derived from second order perturbation theory reads as:
, R3d(r) being the radial part of the 3d wave function. The value of ζ for Fe2+ has been considered as 0.049 eV19, taken from the literature. Spin-orbit contribution to the energy derived from second order perturbation theory reads as:

Here |o〉 and |u〉 correspond to occupied and unoccupied states weighted by the occupations of the Fe-d orbitals. |u/o〉 = |lm, σ〉, L and S denote orbital and spin operators and Eu and Eo denote eigenvalues of unoccupied and occupied states, which are obtained from ab initio calculations. As the denominator decreases, spin-orbit coupling energy contribution increases. The relative arrangement of Fe-d orbitals is thus very important and can be affected by the adsorption site. Our calculated magnetic anisotropy energies are presented in Table I. A plus (minus) sign of MAE corresponds to an in-plane (out-of-plane) easy axis of magnetization.
One of the most relevant properties for magnetic nanosystems is the magnetic dipole contribution 〈Tz〉 as it can have a very large value for low dimensional structures, as reported earlier for clusters20 and organometallics5,21. This has a significant contribution in the effective spin moment, Seff = Ms + 7〈Tz〉, which is measured in XMCD experiments, Ms being the saturation spin moment. It should be noted that the sign of 〈Tz〉 can even be opposite to the spin moment giving rise to a small value of the effective spin moment5. We have calculated spin dipole contribution following the formalism prescribed in the literature22,23,24 and the results are shown in Table I. Due to different adsorption sites, ligand field splittings are different and spin densities have different kinds of asphericities. All these are counted in the spin dipole contribution as this measures the asphericity in the spin density. As a result, the effective spin moments are significantly different for different adsorption sites, which should be captured in XMCD measurements.
All the above discussions lead to the exploration of possible applications of defect controlled magnetism in molecular nanospintronics. Single-molecule magnets have been proposed to act as robust spin qubits25. The stability of these nanomagnets is dictated by the magnetic anisotropy26. According to our study, one can achieve a rational design of spatially distributed single molecule nanomagnets by selectively producing relevant point defects on the graphene sheet with the help of focussed ion-beam technique. As a consequence, the relative orientation of molecular spins in individual nanomagnets at designated lattice sites will provide the possibility of achieving robust spin qubits to be used in spin logic operations.
Discussion
Our ab initio density functional calculations suggest that a graphene layer without structural defects placed in between an FeP molecule and a ferromagnetic Ni substrate decouples the molecule-substrate magnetic interaction for the most favorable hexagonal adsorption site. However, point defects in the graphene lattice can mediate ferromagnetic or antiferromagnetic coupling depending on the nature of the defect. This complex behavior of exchange interactions is related to the magnetization profile in the defected graphene lattice induced by the underlying Ni substrate. A long-ranged ferrimagnetic sublattice magnetization in defect free graphene is drastically modified by the introduction of defects and hence, different types of magnetic coupling are observed depending on the adsorption site on graphene and also the type of defect in graphene. Not only the magnetic coupling but a strong variation in magnetic anisotropy energies and easy axes of magnetization is observed along with large contributions from spin-dipolar interaction. We propose that the control over the spin of single molecule magnets, e.g., FeP by selective defect production in graphene may lead to robust spin qubits for spin logic operations. We hope that our prediction of defect controlled magnetism will boost the experimental verifications with the help of controlled defect productions by ion-irradiation techniques and magnetic measurements by XMCD experiments.
Methods
We have performed first-principles calculations based on density functional theory with a full potential plane wave based code VASP27,28. The Ni(111) surface is considered as the substrate, as graphene can easily be grown on top of it due to excellent lattice matching. A slab of three Ni layers consisting of 108 atoms has been considered along with a graphene monolayer with 72 atoms (6 × 6 supercell) on top of the metallic slab. The size of the supercell is chosen in such a way that the magnetic centers of FeP are at least 15 Å apart from each other in the lateral direction, which minimizes the interaction among them. FeP with an Fe center consists of 37 atoms, yielding a total of 217 atoms in the simulation cell. A 3 × 3 × 1 k-point mesh is chosen for geometry optimizations with a force tolerance of 0.01 eV/Å. All the atomic positions were relaxed except the ones in the lowest Ni-layer, which is fixed to have the in-plane lattice constant as that of bulk Ni. A 4 × 4 × 2 k-point mesh is considered for calculating total energies and other properties. We have employed PBE + U approach within Hubbard model29 to incorporate strong Coulomb interaction with the Coulomb parameter U and exchange parameter J fixed as 4 and 1 eV respectively for Fe d-orbitals. These parameters have been shown30 to reproduce certain experimental results. It should be mentioned that the choice of U and J may have important consequences in the properties of materials31. These parameters have been explicitly calculated by first principles and the results have been successfully compared to experiments in some cases32,33,34. In the present context, the value of U calculated by linear response method by Scherlis et al35. for heme is around 4 eV and hence justifies our choice of U. All the calculations are performed including an empirical form of dispersion correction given by Grimme36. The inclusion of van der Waals interaction is crucial due to the presence of π-π interactions between FeP and graphene. Also, it becomes very important in describing the binding characteristics between graphene and Ni15.
References
Wende, H. et al. Substrate-induced magnetic ordering and switching of iron porphyrin molecules. Nat. Mater. 6, 516–520 (2007).
Dediu, V. A., Hueso, L. E. & Taliani, C. Spin routes in organic semiconductors. Nature Mater. 8, 707–716 (2009).
Leoni, T. et al. Controlling the Charge State of a Single Redox Molecular Switch. Phys. Rev. Lett. 106, 216103 (2011).
Bhandary, S. et al. Manipulation of spin state of iron porphyrin by chemisorption on magnetic substrates. Phys. Rev. B 88, 024401 (2013).
Bhandary, S. et al. Graphene as a Reversible Spin Manipulator of Molecular Magnets. Phys. Rev. Lett. 107, 257202 (2011).
Geim, A. K. & Novoselov, K. S. The rise of graphene. Nature Mater. 6, 183–191 (2007).
Castro Neto, A. H., Guinea, F., Peres, N. M., Novoselov, K. S. & Geim, A. K. The electronic properties of graphene. Rev. Mod. Phys. 81, 109–162 (2009).
Geim, A. K. Graphene: Status and Prospects. Science 324, 1530–1534 (2009).
Yazyev, O. V. Emergence of magnetism in graphene materials and nanostructures. Rep. Prog. Phys. 73, 056501 (2010).
Weser, M. et al. Induced magnetism of carbon atoms at the graphene/Ni(111) interface. Appl. Phys. Lett. 96, 012504 (2010).
Gass, M. H. et al. Free-standing graphene at atomic resolution. Nat. Nanotech. 3, 676–681 (2008).
Hashimoto, A., Suenaga, K., Gloter, A., Urita, K. & Iijima, S. Direct evidence for atomic defects in graphene layers. Nature 430, 870–873 (2004).
Ugeda, M. M. et al. Electronic and structural characterization of divacancies in irradiated graphene. Phys. Rev. B 85, 121402(R) (2012).
Meyer, J. C. et al. Direct Imaging of Lattice Atoms and Topological Defects in Graphene Membranes. Nano Lett. 8, 3582–3586 (2008).
Mittendorfer, F. et al. Graphene on Ni(111): Strong interaction and weak adsorption. Phys. Rev. B 84, 201401(R) (2011).
Hajati, Y. et al. Improved gas sensing activity in structurally defected bilayer graphene. Nanotechnology 23, 505501 (2012).
Sanyal, B., Eriksson, O., Jansson, U. & Grennberg, H. Molecular adsorption in graphene with divacancy defects. Phys. Rev. B 79, 113409 (2009).
Miller, C. W. et al. Quantitative structural analysis of organic thin films: An x-ray diffraction study. Phys. Rev. B 72, 104113 (2005).
Cole, G. M. & Garrett, B. B. Atomic and Molecular Spin-Orbit Coupling Constants for 3d Transition Metal Ions. Inorg. Chem. 9, 1898–1902 (1970).
Sipr, O., Minar, J. & Ebert, H. On the importance of the magnetic dipole term Tz in analyzing X-ray magnetic circular dichroism spectra of clusters. Eur. Phys. Lett. 87, 67007 (2007).
Stepanow, S. et al. Spin and Orbital Magnetic Moment Anisotropies of Monodispersed Bis(Phthalocyaninato)Terbium on a Copper Surface. JACS Comm. 132, 11900–11901 (2010).
Wu, R. & Freeman, A. J. Limitation of the Magnetic-Circular-Dichroism Spin Sum Rule for Transition Metals and Importance of the Magnetic Dipole Term. Phys. Rev. Lett. 73, 1994 (1994).
Stöhr, J. & König, H. Determination of Spin- and Orbital-Moment Anisotropies in Transition Metals by Angle-Dependent X-Ray Magnetic Circular Dichroism. Phys. Rev. Lett. 75, 3748 (1995).
Oguchi, T. & Shishidou, T. Anisotropic property of magnetic dipole in bulk, surface and overlayer systems. Phys. Rev. B 70, 024412 (2004).
Baldovi, J. J. et al. Rational Design of Single-Ion Magnets and Spin Qubits Based on Mononuclear Lanthanoid Complexes. Inorg. Chem. 51, 12565–12574 (2012).
G-Coca, S., Cremades, E., A-Alcalde, N. & Ruiz, E. Mononuclear Single-Molecule Magnets: Tailoring the Magnetic Anisotropy of First-Row Transition-Metal Complexes. JACS 135, 7010–7018 (2013).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, R558 (1993).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Anisimov, V. I., Aryasetiawan, F. & Lichtenstein, A. I. First-principles calculations of the electronic structure and spectra of strongly correlated systems: the LDA + U method. J. Phys.:Condens. Matter 9, 767–808 (1997).
Panchmatia, P. M., Sanyal, B. & Oppeneer, P. M. GGA + U modeling of structural, electronic and magnetic properties of iron porphyrin-type molecules. Chem. Phys. 343, 47–60 (2008).
Rondinelli, J. M. & Spaldin, N. A. Structural effects on the spin-state transition in epitaxially strained LaCoO3 films. Phys. Rev. B 79, 054409 (2009).
Hsu, H., Blaha, P., Cococcioni, M. & Wentzcovitch, R. M. Spin-state crossover and hyperfine interactions of ferric iron in MgSiO3 perovskite. Phys. Rev. Lett. 106, 118501 (2011).
Kulik, H. J., Cococcioni, M., Scherlis, D. A. & Marzari, N. Density functional theory in transition-metal chemistry: A self-consistent Hubbard U approach. Phys. Rev. Lett. 97, 103001 (2006).
Himmetoglu, B., Wentzcovitch, R. M. & Cococcioni, M. First-principles study of electronic and structural properties of CuO. Phys. Rev. B 84, 115108 (2011).
Scherlis, D. A., Cococcioni, M., Sit, P. & Marzari, N. Simulation of heme using DFT + U: A step toward accurate spin-state energetics. J. Phys. Chem. B 111, 7384–7391 (2007).
Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comp Chem. 27, 1787–1799 (2006).
Acknowledgements
We thank Oscar Grånäs for useful discussions. B.S. acknowledges Carl Tryggers Stiftelse and VR/SIDA for financial support. O.E. is in addition grateful to the KAW foundation, eSSENCE and the ERC(project 247062 - ASD) for support. We also acknowledge SNIC-UPPMAX, SNIC-HPC2N and SNIC-NSC centers under the Swedish National Infrastructure for Computing (SNIC) resources for the allocation of time in high performance supercomputers.
Author information
Authors and Affiliations
Contributions
B.S. designed the project and S.B. carried out the calculations. S.B., O.E. and B.S. analyzed the data and wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Bhandary, S., Eriksson, O. & Sanyal, B. Defect controlled magnetism in FeP/graphene/Ni(111). Sci Rep 3, 3405 (2013). https://doi.org/10.1038/srep03405
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03405
This article is cited by
-
Generation of paramagnetic centers in carboxylated materials via coordination attachment of diamagnetic tetraazamacrocyclic complexes of nickel(II)
Journal of Materials Science (2020)
-
Designing a molecular magnetic button based on 4d and 5d transition-metal phthalocyanines
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.