Introduction

The field of complex networks has recently undergone an important evolution. Thanks to the recent availability of time-resolved data sources, many studies performed under the assumption of static network structures can now be extended to take into account the network's dynamics. Data on time-varying networks are becoming accessible across a variety of contexts, ranging from communication networks1,2,3,4,5,6 to proximity networks7,8 and infrastructure networks9,10. This avalanche of data is prompting a surge of activity in the field of “temporal networks”11. Data analysis has shown the coexistence of statistically stationary properties and topological changes, as well as the burstiness of interactions characterized by highly skewed distributions of inter-event times1,2,3,4,5,6,7,8,9,10,11,12,13,14. These temporal features of networks influence the dynamics of network processes, just like the topological structure of static networks does15. As a consequence and similarly to the case of static networks, simple dynamical processes such as random walks16, synchronization phenomena17, consensus formation18 or spreading processes19,20,21,22,23,24,25 can be used as probes to investigate the temporal and structural properties of time-varying networks.

Previous works on the dynamics of spreading processes over complex networks have considered both the topological and the temporal structure of networks11,19,23, as well as the specific impact that the temporal structure bears on the spreading process. The quantities used to quantify the measured effects are typically network averages, such as the outbreak sizes of an epidemic or its prevalence. These average quantities, however, fail to account for important heterogeneities in the arrival times of the spreading process. Recent work26 showed that the non-stationarity and burstiness of empirical temporal networks lead to noisy distributions of arrival times and that shifting the perspective from a global notion of wall-clock time to a node-specific “time” based on node activity allows to expose a clear and robust pattern in arrival “times”.

Here we focus on the distribution of arrival times for spreading processes, based on a wide range of empirical data on time-resolved human proximity. In particular, we seek to identify the dynamic features of the temporal network that are responsible for the observed arrival time distributions. To this aim, we consider temporal networks of human contacts and we define hierarchies of null models and generative models that selectively retain or discard specific properties of the empirical data. We simulate simple spreading processes over these models and perform a comparative analysis of the arrival time distributions. Our results identify the most salient properties that characterize realistic models of human interaction networks and highlight the properties that control the arrival time distributions, with applications to several domains such as opportunistic information transmission and epidemic spread and containment.

We consider time-varying networks of human proximity measured using wearable sensors. The data were collected by the SocioPatterns collaboration (http://www.sociopatterns.org) in different social contexts: two conferences in Italy (HT09) and France (SFHH)7,22, a primary school in France (PS)27 and a paediatric hospital ward in Italy (HOSP)28. Details on the data collection methods are reported in the Supplementary Information description and Table S1. All of the datasets we consider describe the face-to-face proximity relations of the monitored subjects, with a temporal resolution of approximately 20 seconds7,22. For every pair of individuals, the full sequence of individual interactions is resolved, with starting and final timestamps for every close-range proximity relation. These data can be represented as time-varying networks of proximity: nodes represent individuals and a link connecting two nodes indicates that the corresponding individuals are in contact, i.e., in face-to-face proximity of one another.

Results

Epidemic processes and activity clocks

We probe the temporal structure of the empirical networks with a simple Susceptible-Infected (SI) process. The population of nodes (individuals) is split into two compartments: susceptible nodes (S), who have not caught the “infection” and infected nodes (I), who carry the “infection” and may propagate it to others. In this simple epidemic model, infected nodes never recover. A node is randomly selected as the seed from which the infection starts spreading deterministically, through contacts between a susceptible node and an infected one (S + I → 2I). Transmission events are assumed to occur instantaneously on contact.

We fingerprint the temporal network structure of the data by computing the times at which the epidemic process reaches the different nodes. Specifically, we focus on the probability distribution of arrival times for the SI process unfolding over the temporal network. In terms of wall-clock time, the arrival time at a given node is defined as the time elapsed between the start (seeding) of the SI process and the time at which the process reaches the chosen node. It has been shown26 that the distribution of these arrival times is extremely sensitive to several heterogeneities of the empirical data, to the seeding time. In general, it displays strong heterogeneities due to the non-stationary and bursty behavior of empirical temporal networks that cannot be captured by simple statistical models. Thus, we shift to a node-specific definition of “time”: each node is assigned its own “activity clock” that measures the time that node has spent in interaction or, similarly, the number of contact interactions that node has been involved in. The “time” measured by this clock does not increase when the node is isolated from the rest of the network. In the following, for clarity, we will indicate with “time*” the activity-clock readings. The “arrival time*” of the epidemic process at a given node is defined as the increase of its activity clock reading from the moment the SI process is seeded to when it reaches the node. Arrival times* discard by definition many temporal heterogeneities of the empirical data and usually exhibit a well-defined distribution26 that is robust with respect to changes in the starting time of the process and across temporal networks of human contact measured in different contexts. In the following we use activity clocks based on the number of contact events a node has been involved in. The arrival time* at a node, consequently, will be integer-valued and will measure the number of interactions each node was part of from the seeding of the epidemic until the node was infected.

For each empirical time-varying network, we generate a hierarchy of synthetic temporal networks using both a top-down and a bottom-up approach. The synthetic networks are designed to support our analysis by selectively retaining or discarding specific properties of the empirical data.

Top-down approach: null models

We generate null models by applying to the empirical data randomization procedures that erase specific correlations24. We keep the topology of the contact network unchanged. In the “interval shuffling” (IS) procedure, the sequences of contact and inter-contact durations are reshuffled for each link separately, while in the “link shuffling” (LS) procedure24 the unaltered sequences of events are swapped between link pairs. Both procedures destroy the causal structure of the temporal network, but they both preserve the global distributions of contact durations, inter-contact durations and number of contacts. The IS procedure also preserves, for every link, the total number of contact events and the cumulated interaction time, while the LS procedure does not conserve these quantities at the link level.

We also consider a global time shuffling procedure (TS): we build a global list of the empirical contact durations and, for each link, we generate a synthetic activity timeline by sampling with replacement the global list of contact durations according to the original number of contacts for that link. While the global distribution of contact durations and of the number of contacts per link are conserved by construction, all temporal correlations are destroyed and the distributions of inter-contact times differs from the empirical one.

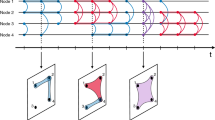
Figure 1 illustrates the three randomization procedures defined above. All the procedures conserve the topology, the distribution of contact durations and the distribution of the number of contacts per link of the empirical networks. Table 1 summarizes the impact of the randomization procedures on different properties of the temporal networks.

Table 1 Properties of the empirical temporal networks that are retained (✓) or discarded (✗) by the various null models. P(τ) is the distribution of inter-contact interval durations. ωAB indicates the cumulated contact durations of an arbitrary link AB and P(ω) is the distribution of cumulated contact durations. nAB indicates the number of contacts per link of an arbitrary link AB and P(n) is the distribution of the number of contacts per link. IS, LS and TS stand, respectively, for Interval Shuffling, Link Shuffling and Time Shuffling
Full size table
Figure 1
figure 1

Example of the shuffling procedures for the simple case of a network with four nodes (A, B, C, D) and two links (A–B and C–D) with their respective contact sequences.

Red (light) segments indicate A–B contacts, while blue (dark) segments indicate C–D contacts. For each link, individual contact intervals are marked with latin letters and inter-contact intervals with greek letters. IS, LS and TS stand, respectively, for Interval Shuffling, Link Shuffling and Time Shuffling. In the TS case the inter-contact intervals are determined by the sampled contact intervals and do not correspond to inter-contact intervals of the original data.

Full size image

Bottom-up approach: generative models

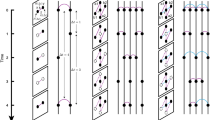
We also define generative models for random temporal networks designed so that the resulting time-varying networks exhibit specific properties of the empirical data, in the spirit of the configuration model for static networks29. We start by creating a static random Erdös-Rényi network with the same number of nodes and the same average degree of the temporally-aggregated empirical contact network. Then we assign to each link a sequence of synthetic contact events, according to different strategies. In the Inter-Contact Time model (ICT) we impose that the global distribution of inter-contact durations is the same as in the empirical data (see the Methods section for details). This is an important case to test against, as it is often considered in the literature that the distribution of inter-contact times plays an important role in determining and constraining spreading processes over temporal networks26. Contact durations are fixed and equal to the average contact duration measured in the empirical data. In the Inter-Contact Time plus Contact-Per-Link model (ICT + CPL) we proceed as in the ICT case, but also impose that the distribution of the number of contact events per link must match the empirical one. In summary, in both models the topology and the contact duration distribution differ from the empirical ones. Table 2 summarizes the properties of the generated temporal networks that are constrained to match those of the empirical data.

Table 2 Properties of the empirical temporal networks that are retained (✓) or discarded (7) by the generative models. As in Table 1, P(τ) is the distribution of inter-contact interval durations. ωAB indicates the cumulated contact durations of individual links and P(ω) is the distribution of cumulated contact durations. nAB indicates the number of contacts per link and P(n) is the distribution of the number of contacts per link. ICT and ICT + CPL stand, respectively, for the Inter-Contact Time model and the Inter-Contact Time plus Contacts-Per-Link model
Full size table

Arrival times measured with activity clocks

From each empirical network, we build synthetic networks according to each null and generative model. We simulate SI processes on both empirical and synthetic networks for different starting times and for different choices of the seed node. We then compute the distributions of arrival times* measured in terms of activity clocks. Figure 2 (panels a and b) compares the arrival time* distributions from the empirical data (HT09 conference and hospital datasets) with those yielded by the null and generative models. The results for the SFHH conference dataset are reported in the SI.

Figure 2
figure 2

Log-binned probability distributions (pdf) of arrival times* (top row) and Kullback-Leibler divergences (middle row for KL and bottom row for KL10+) for the conference dataset (HT09, left column) and the hospital data (HOSP, right column).

In each panel, IS, LS, TS, ICT, ICT + CPL stand respectively for Interval Shuffling, Link Shuffling, Time Shuffling, Inter-Contact Time model and Inter-Contact Time plus Contacts-per-Link model. In the top row, “data” indicates the distribution of arrival times* obtained by simulating an SI process over the empirical temporal network (200 realizations with random starting times for each node of the network taken as seed of the epidemics). For each model, we consider 20 different realizations of the temporal network. For each of these realizations we run 20 different SI epidemics, each with a different random starting time. The arrival times* (top row) for all those runs are aggregated to yield the reported distributions. In the boxplots (middle and bottom row) the box extends from the lower to upper quartiles and the line indicates the median value. The whiskers of the box correspond to the 95% confidence interval.

Full size image

In order to provide a quantitative assessment of the distribution similarity we compute the symmetrized Kullback-Leibler (KL) divergence30 (see Methods) between the distribution of arrival times* for the empirical data and for each model. Given the relevance of large arrival time* values, which may be strongly influenced by causal constraints and in general by the peculiarities of the temporal structure of the network, we also compute the Kullback-Leibler divergence between the tails of the distributions. To this end, we only take into account arrival times* longer than a fixed threshold arbitrarily set to 10. We refer to this restricted Kullback-Leibler divergence as “KL10+” and we have checked that our results are robust with respect to changes in the threshold. Table 3 and Fig. 2 report the symmetrized KL and KL10+ divergences for the conference and hospital datasets we consider.

Table 3 Symmetrized Kullback-Leibler divergence of the arrival times* distributions computed on the original temporal network and on the corresponding synthetic networks, for the conference datasets (HT09 and SFHH) and for the hospital dataset. KL indicates the divergence computed using the entire probability distribution, while KL10+ corresponds to the divergence computed on the distribution tails only, obtained by selecting arrival times* larger than 10
Full size table

Determinants of the arrival time distribution

Using KL and KL10+ as guiding metrics we use the top-down approach to discard features that are unimportant in reproducing the arrival time* distribution and to narrow down a set of necessary features. We then use the bottom-up approach to find the features that are sufficient to model the arrival time* distribution.

The Interval Shuffling (IS) and Link Shuffling (LS) procedures lead to distributions of arrival times* similar to those of the empirical data. This indicates that the causal structure of the temporal network has a small impact on this distribution. Moreover, LS does not preserve the specific assigment of cumulated contact durations ωAB and number of contacts nAB to individual links (see Table 1): we can therefore discard these as explanatory factors of the specific shape of the arrival times* distribution.

According to Table 3 and Fig. 2 (panels c–f) the Time Shuffling (TS) procedure yields a very different distribution for the conference datasets and a different tail for the hospital data. We know that, by design, the TS procedure does not preserve the distribution of inter-contact intervals, which is directly related to the burstiness of contact activity. The failure to adequately model the arrival times* distributions stems thus from this feature and can be related to previous results19,23 showing that burstiness plays an important role in spreading phenomena. Indeed, the distribution of inter-contact interval durations for the synthetic networks are quite different from those measured for the empirical networks (not shown, established by comparing the KL divergences between the corresponding distributions). In the hospital case, this difference between empirical and synthetic inter-contact interval durations is reduced, leading to the reduced difference in arrival times* distributions observed in panel d of Fig. 2 for the TS model.

However, panels c–f of Fig. 2 also show that the distributions of arrival times* obtained for the ICT model, which is designed to preserve the distribution of inter-contact durations, exhibit KL differences that are similar or even larger than those of the TS case discussed above. The corresponding distributions in panels a and b of Fig. 2 are indeed much narrower than the ones obtained with the empirical dataset. This shows that correctly reproducing the distribution of inter-contact durations is not sufficient to adequately model the arrival time* distributions. In order to achieve that, we need to add to the ICT model the additional constraint of preserving the distribution of the number of contacts per link, i.e., to use the ICT + CPL model (see Table 2). This model captures the essential features of the data that are sufficient to reproduce the arrival time* patterns of the empirical data, especially for the tail of the distributions, as shown in panels e and f of Fig. 2. We remark that this model is quite parsimonious, as it does not retain the topology of the empirical network nor the distribution of contact durations or cumulated contact durations.

Activity-correlated classes of links

Despite the success of the ICT + CPL model for the conference and hospital datasets, which we remark are quite different from one another, in the case of primary school data none of these models yields a distribution of arrival times* close to that generated from the empirical data, as shown in the panel a of Fig. 3 and Table 4. In particular the IS and ICT + CPL models both yield similar, narrower distributions.

Table 4 Kullback-Leibler divergences between the arrival time* distributions from the empirical school data and from each of the synthetic networks based on the data. KL10+ indicates the divergence restricted to the tail of the distributions
Full size table
Figure 3
figure 3

a) Log-binned arrival time* distributions for the school dataset (original data, null models and generative models). b) Log-binned arrival time* distributions for synthetic datasets generated by the toy model described in the main text, together with the distributions obtained through the ICT + CPL model from these synthetic datasets. The synthetic datasets exhibit community structure (cs), temporal modulation (tm), or both (cs-tm). Details are given in the Methods section. p1 = 0.8, p2 = 0.2 for the cases with community structure and p1 = 0.5, p2 = 0.5 otherwise, see Methods.

Full size image

Compared to the datasets considered in the previous sections, the school dataset presents a few distinctive features. In the conference cases individuals mix in a rather homogeneous way, but most interactions occur at specific moments typically corresponding to social activities such as coffee breaks7,22. In the hospital case, the interactions display characteristic role-dependent patterns, but contacts are distributed rather homogeneously during the day28. The primary school dataset, on the other hand, exhibits both a strong community structure dictated by class membership and correlated contact patterns across classes determined by the schedule of social activities27. Contacts between children of different classes are possible during specific time intervals only and strongly correlated during such periods, because the school schedule controls class-based activities rather than individual activities.

To tease apart the respective roles of community structure and correlated activity of link groups we study the arrival time* distributions in the case of synthetic datasets exhibiting one or both of these features. These synthetic datasets are created using a toy model that generates temporal networks with tunable community structure (cs) and temporal correlations in the activity of inter-community links. To this aim, we impose a temporal modulation (tm) in the activity of inter-community links: contact events on these links can only occur during specific time intervals (see details in the Methods section). We subsequently compute arrival time* distributions for these synthetic datasets as well as for the corresponding ICT + CPL models. Panel b of Figure 3 shows that, when activity-correlated classes of links are introduced, the arrival time* distributions for the ICT + CPL case deviates significantly from that based on the corresponding synthetic dataset. This is similar to what we reported for the school data (even though the shape of the arrival time* distribution is different) and occurs regardless of the presence (or lack thereof) or a community structure in the synthetic dataset. When the synthetic dataset displays a community structure but no correlations between the activity of inter-community links, the same arrival time* distributions are indeed observed for both the synthetic network and the corresponding ICT + CPL model.

Discussion

The distribution of arrival times at various nodes of an epidemic process unfolding over a temporal network, when measured in terms of activity clocks, displays a behavior that is robust across very different settings and for different starting times of the process, despite the intrinsic heterogeneities and non-stationarities of the temporal network. The arrival time distribution expressed in terms of activity clocks thus represents an interesting tool for investigating the structure of temporal networks beyond their surface features.

The burstiness observed in many real-world networks, indicated by a broad distribution of inter-event times, is known to be an important feature of temporal networks that influences dynamical processes taking place on them. Here we have carried out an analysis based on empirical networks of human interactions, measured in different social environments and we have used suitably-designed null models and generative models for temporal networks to show that the burstiness of inter-event sequences is not the only essential property that needs to be retained when aiming at a realistic model of time-varying contact networks: the heterogeneity of the number of contacts per individual link also plays a fundamental role in determining the arrival times of the spreading process. Our results show that, in fact, it is possible to design parsimonious generative models of temporal networks, such as the ICT + CPL model, based on just the distribution of inter-event interval durations and on the distribution of number of contacts per link. The ensuing synthetic temporal networks adequately model the arrival time distributions of real-world networks measured in diverse settings.

Interestingly, the behavior of the arrival time distribution expressed in terms of activity clocks is sensitive to complex features of the temporal network data such as the presence of activity-correlated classes of links, as exemplified by the case of the school temporal network, where the interplay of the community structure induced by classes and of correlated activity patterns due to schedule activities creates rich temporal structures in the data. We have shown that the presence of classes of links that are only active in a correlated fashion during specific time windows has an impact on the spreading time distribution and breaks down the ability to use parsimonious models such as the ICT + CPL one. Activity-correlated classes of links, which are arguably common in many real-world social systems, are difficult to uncover on the basis of simple statistical observables for the temporal network and their impact on the dynamics of spreading process calls for more research. We have shown that arrival time distributions based on activity clocks are a precious tool in this respect as they have the ability to indicate the presence of such complex structures and correlations. Simple generative models, such as the ICT + CPL model, cannot possibly account for these complex structures and should thus be enriched, when necessary, by introducing additional features such as classes of links with correlated and temporally-localized activity. Here we have shown that toy models that minimally incorporate such features yield deviations in the arrival time patterns similar to those observed for the school temporal network.

Overall, our results call for more work in the direction of both detecting and modeling complex temporal-topological structures in time-varying networks. Similarly, more work is needed to design minimal generative models that incorporate realistic features found in empirical data from real-world scenarios.

Methods

Definition of null and generative models

Here we describe the different shuffling procedures and generative models introduced in the main text. For the top-down approach, we start from the empirical temporal networks, on which we apply the following shuffling procedures:

Interval Shuffling (IS)

The sequence of contact and inter-contact intervals of each link is randomly shuffled. The original contact durations and inter-contact durations are thus preserved. Given a link (a, b) with n contact events, let us denote the contact intervals by (s0, e0), (s1, e1), …, (sn, en). The set of contact durations is thus given by (e0 − s0), (e1 − s1), …, (en − sn) and the set of inter-contact durations is (s1 − e0), (s2 − e1), …, (sn − en−1). We create a synthetic timeline for the link (a, b) by randomly shuffling the sequence of contact and inter-contact intervals and then we randomly and uniformly translate the starting time of the link's new timeline within the remaining time interval T − (en − s0), where T is the full dataset time interval. Consistently, links with n = 1 contact events have an empty set of inter-contact times and the single contact interval is simply randomly displaced in time.

Link Shuffling (LS)

Whole single-link event sequences are randomly exchanged between randomly chosen link pairs. Event-event and weight-topology correlations are destroyed.

Time Shuffling (TS)

Time intervals of the whole original contact sequence are randomly shuffled and reallocated randomly to each link retaining the distribution of the number of contacts per link of the original dataset. Temporal correlations are destroyed. The resulting shuffled network is built with a condition of no intersection between contact intervals in the same link.

In the case of the generative models, we start by creating a static random network with approximately the same degree distribution, the same number of nodes and the same number of links as the empirical network we want to study. Then, we build a temporal network by associating with each link a sequence of contact events, according to the following strategies:

ICT

For each link we set the number of contacts per link equal to the average number of contacts per link of the original data. Each of these contacts is then generated with a duration equal to the average contact duration observed in the empirical data. The time between contact events is set by sampling with replacement the distribution of inter-event times measured in the data.

ICT + CPL

The ICT + CPL model is based on the ICT model described above, with the additional constraint that for each link the number of contacts is not constant, but is set by sampling with replacement the distribution of the number of contacts per link of the empirical data.

Symmetrized Kullback-Leibler divergence

The symmetrized Kullback-Leibler divergence is defined as:

where D(i) is to the distribution of (integer-valued) arrival times* in the empirical data and M(i) is the distribution yielded by the models. To assess the stochastic variability range of the Kullback-Leibler divergence, we generate several realizations of each null model or generative model, we compute the divergence between the distribution yielded by each realization and that of the original data and we show a box plot summarizing the resulting values.

Definition of a toy model with activity-correlated link classes

In order to understand which features of the school data make the distribution of arrival times* not reproducible by the synthetic networks of the ICT + CPL model, we introduce a toy generative model that produces temporal networks with some key features of the original school network, namely the community structure and the synchronization of the activity/inactivity patterns of some groups of links. We start by building a static network with a simple two-community structure: we consider N nodes and divide them into two groups of equal size. Within each group, two nodes are linked with a probability p1. Nodes across the two communities are linked with a probability p2 ≤ p1 (the case p1 = p2 yields a random graph without community structure). This procedure defines the topological structure of the network. We build the temporal network by associating with each link a sequence of contact events. These activity sequences are all generated by sampling a Poisson process with a rate λ = 0.0056 s−1, which was chosen to yield an average number of contacts per link of the same order of the school data over the same global time . For the cross-community links we then remove all events outside of the interval [T/2(1 − δ), T/2(1 + δ)]. This last condition introduces a temporal modulation for the inter-community links, which are only active in the above time window. In the limit δ → 1 we recover the non-modulated case.