Abstract
Long-term and high temporal resolution gravity and deformation data move us toward a better understanding of the behavior of Mt Etna during the June 1995 – December 2011 period in which the volcano exhibited magma charging phases, flank eruptions and summit crater activity. Monthly repeated gravity measurements were coupled with deformation time series using the Differential Synthetic Aperture Radar Interferometry (DInSAR) technique on two sequences of interferograms from ERS/ENVISAT and COSMO-SkyMed satellites. Combining spatiotemporal gravity and DInSAR observations provides the signature of three underlying processes at Etna: (i) magma accumulation in intermediate storage zones, (ii) magmatic intrusions at shallow depth in the South Rift area, and (iii) the seaward sliding of the volcano's eastern flank. Here we demonstrate the strength of the complementary gravity and DInSAR analysis in discerning among different processes and, thus, in detecting deep magma uprising in months to years before the onset of a new Etna eruption.
Similar content being viewed by others
Introduction
Repeated gravity surveys and ground deformation measurements have become effective volcano monitoring tools for mid- to long-term hazard assessment, by providing unique insights into processes that involve mass redistribution and/or pressure changes within volcano edifices1,2. Modeling of deformation sources by using ground deformation data alone usually suffers from the inability of resolving mass and density variations in the subsurface. The combined analysis of time-dependent gravity and surface deformation data can effectively constrain the mass of the source3,4. Depending on its physical properties, the arrival of fresh magma can cause a mass increase that may have little or no interaction with the surrounding medium. In this case, a limited ground deformation occurs, while a significant gravity increase is measurable at the surface5, thus making the analysis of gravity time changes particularly relevant even when negligible ground deformation is observed6,7,8.
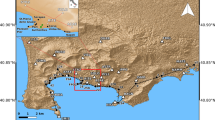
Time-dependent gravity and ground deformation measurements are, therefore, complementary to each other and their regular recording may disclose and clarify complex volcanic dynamics. An extraordinary gravity and ground deformation data set, in terms of continuity and duration, has been gathered at Etna since 1995. Monthly repeated gravity measurements have been carried out along a 24-kilometer West-East trending profile of 19 stations on the volcano's southern flank to monitor the dynamics of the main volcanic and tectonic features (Fig. 1). Earlier efforts at jointly detecting and interpreting deformation and gravity changes in a long-term perspective were hampered by the misplacement of gravity and GPS stations and by the lower temporal resolution of GPS data (yearly geodetic surveys)8.
The closest SAR pixels to the gravity stations are also reported for the ERS/ENVISAT and CSK time series. The major surface fault systems (red lines) border the main rigid blocks (colored shaded areas) of the eastern flank sliding21, which is delimited by the Ragalna fault to the SW and by the Pernicana fault to the NE. Geographical coordinates are expressed in UTM projection, zone 33N. All the figures in this paper were generated using a DEM owned by INGV.
The DInSAR measurements9,10 may overcome these issues allowing the detection of centimeter- to millimeter-scale ground deformation at a high spatial and temporal resolution11. The availability of large SAR data archives, acquired from 1992 to 2010 by ERS/ENVISAT and since 2009 by COSMO-SkyMed satellites, enables us to recognize and measure the deformation evolution of significant portions of Etna volcano with a high density of measurements over nearly 2 decades12. Separate analysis of the DInSAR13 and gravity data14,15 have been recently performed, showing significant correlations between the eruptive and flank dynamics of Etna volcano and the spatiotemporal pattern changes of either DInSAR or gravity data.
We jointly analyze and compare, for the first time, all the available gravity and DInSAR datasets covering the 1995–2011 period in order to detect and interpret common patterns in their spatiotemporal evolution. This long-term and high temporal resolution dataset constitutes a unique opportunity to examine the behavior of Etna's southern flank in a period in which the volcano exhibited different styles of activity characterized by magma recharging, flank eruptions, and fountaining episodes. Here we demonstrate the strength of the complementary gravity and DInSAR analysis in distinguishing the response of Etna volcano to different processes, posing the basis to track the unrest evolution and to forecast the style of future eruptions.
Results
Volcano-tectonic setting and recent eruptive activity
The gravity profile lies in a complex geodynamical context and intersects some of the main structural features of this Etna sector and areas undergoing different dynamical behaviors: the Ragalna fault System, the South Rift, and the eastern flank sliding sector (Fig. 1). The Ragalna fault System composed of a complex arrangement of at least three main faults dissecting the SW flank of the volcano, represents the southwestern boundary of the eastward moving sector16,17, separating a stable block on its western side from the mobile southern sector on its eastern side. The South Rift, radiating from the summit, is probably shallow rooted and has been usually laterally fed by the central conduit12 and exceptionally by the emplacement of peripheral vertically propagating deeper dikes18, as occurred during the 2001 and 2002–2003 flank eruptions. The eastern flank of the volcano shows a fairly continuous seaward motion, due to the interplay of gravity instability and magma intrusion19,20,21.
Between 1995 and 2011, Etna volcano exhibited different eruptive styles characterized by quasi-persistent activity from the summit craters and frequent lateral eruptions from vents situated on the volcano flanks. During the first six years (mid-1995 to mid-2001) the eruptive activity was confined to the summit area, where lava flows, lava fountains and powerful explosive events occurred in rapid succession at the summit craters (Fig. 1). Since 2000, Etna's activity moved toward more explosive styles22. The next four years were marked by two highly explosive and destructive flank eruptions in 2001 and 2002–2003, which coincided with a sharp drop in summit activity, and then by two dynamically singular, passive flank effusions in 2004–2005 and 2006. After the last effusive event occurred in 2008–2009, the volcano remained largely quiescent until 2011, when the Etna activity renewed with frequent, intermittent episodes of lava fountains from the South-East Crater (18 episodes in 2011).
Geophysical constraints on Etna dynamics
This intensive volcanic activity has been marked by significant spatiotemporal changes in DInSAR and gravity data12,15. A joint examination of the deformation and gravity maps (Figs. 2, 3 and Methods) highlights time intervals in which the analyzed signals underwent contemporaneous changes occurring mainly in the central and eastern stations of the profile, while lower amplitude changes are observed in the westernmost stations. From 1995 to 2001, a gravity variation cycle and an overall inflation of the volcano23,24, with horizontal expansion and diffuse uplift, are observed. This style was abruptly interrupted by the 2001 flank eruption and, after the 2002–2003 eruption, a new more complex behavior arose with predominantly negative gravity changes in the central and eastern portions of the profile, accompanied by discontinuous positive and negative increases in height changes and by outstanding horizontal deformation. This behavior stopped in 2009 when, new positive gravity changes were observed and the vertical deformation slowed down after about 8 years of continuous decrease.
(a) Spatiotemporal gravity variations along the West-East profile (y axis) between June 1995 and December 2011 (x axis). All measurements were referred to the outermost station of the profile (Adrano; ADR). (b) Gravity variations after the correction of the free-air contribution estimated from DInSAR derived height changes. (c) Gravity changes filtered of local noise, short-wavelength spatial and seasonal components using a 2-D wavelet multi-resolution analysis as described in Methods14. (d) Etna activity from 1995 to 2011 showing the flank eruptions (FE) and the different eruptive styles at the summit craters (SC).
The gravity-height changes, plotted in a Δg/Δh diagram (Fig. 4), do not show any clear correlation, as usually expected in volcanic areas5. The spatiotemporal gravity and DInSAR changes have varied substantially both in time and in space, and cannot be easily explained by a unique process affecting the whole profile. We can distinguish five main different patterns in the Δg/Δh diagram at stations located in distinct sectors bounded by volcano-tectonic structures (Fig. 1). This could reflect the response of the volcano to different mechanisms. Indeed, in the region covered by the measurements, the dynamics of Etna volcano is generally controlled by three main processes12, which have been constrained by the gravity and DInSAR observations.
Five patterns localized in distinct sectors of the volcano bounded by main volcano-tectonic structures (Fig. 1) are highlighted.
Magma accumulations in storage zones
The first process is related to the inflation of the volcano due to the accumulation of magma rising from depth, which induces positive gravity variations, moderate uplift and horizontal displacements of the volcano flanks. The long-term datasets point out at least three main magma charging phases. A first charging phase started during the late months of 1995, when a gravity increase/decrease cycle begun, which reached the maximum amplitude of about 50 μGal at the beginning of 1997 and ended in mid-1998 (Fig. 3c, box I). A second increase/decrease gravity cycle, affecting mostly the central and western portions of the profile, started at the mid-1999, culminating at the mid-2001 (maximum amplitude about 30 μGal) and continuously decreasing until mid-2002 (Fig. 3c, box II). These two gravity cycles are accompanied by a moderate uplift of about 3 cm and a horizontal displacement of approximately −3 cm and 6 cm in the western and eastern flanks, respectively. After 2001, the gravity increase/decrease cycles faded away accompanied with an overall negative trend in the vertical deformation (about −1 cm/yr) until 2009. After about 8 years of absence of significant gravity cycles, a new marked and persistent increase in gravity changes started at the beginning of 2010 and continued during the last survey carried out in December 2011, when it reached a maximum amplitude of about 60 μGal (Fig. 3c, box III). The increase of gravity field recorded in this period is among the largest ever recorded along the profile. Contemporaneously, the negative trend in the vertical deformation came to an end (TG station in Fig. 2a). By comparing the long-term gravity increase/decrease cycles with a chronogram of the paroxysmal activity at the summit craters and the flank eruptions of Etna, a qualitative correspondence in time between positive gravity changes and intense eruptive activity is observed (Fig. 3).
Usually, gravity-height changes associated with recharging phases at many volcanoes have been found to follow a linear relationship5, which is straightforwardly explained by a pressurized spherical magma chamber embedded in an elastic half-space. The magma is assumed to be fully incompressible and thus, as it is injected or withdrawn, the chamber changes its volume accordingly, deforming the surrounding medium and triggering gravity and elevation changes at the surface5. Following this model and assuming typical density of the basaltic magma (2500–2700 kg/m3), the Δg/Δh ratio, after the free-air correction, ranges between 0.65 and 0.79 μGal/cm25. However, our observations do not confirm this simple model since significant positive gravity changes occur together with slight positive height changes (Fig. 4), thus implying that Δg/Δh should show significantly larger values. If the chamber is not spherical and the magma is considered compressible, the Δg/Δh ratio may be higher26. According to previous gravity14 and geodetic29 investigations, Etna's plumbing system has a multifaceted geometry consisting of storage zones at different depths. The intermediate storage zone lies between 2 and 4 km, at a depth where the SO2, the most abundant gas phase at Etna, starts to exsolve. Assuming at this depth magma with average compressibility30 of about 0.2 GPa−1 and a medium rigidity derived from seismic tomography of 30 GPa29, the Δg/Δh ratio for prolate ellipsoids, such as those detected at Etna from geodetic investigations29,8, may reach a value of about 13 μGal/cm (Fig. 5 and Methods). For an ellipsoidal source with aspect ratio of about 1.6, the modeled Δg and Δh values are in general agreement with the data (red dots in Fig. 5) relevant to the recharging phase occurred in 1997 (Fig. 3c, box I), when magma accumulation was the predominant process. The arrival of high compressibility magma may engender larger values of the Δg/Δh ratio, thus implying significant positive gravity variations accompanied by slight positive height changes, as highlighted by our gravity and DInSAR data at Etna volcano. Even if no claim is made that the model strictly applies to the observations, this result shows a significant qualitative agreement with the gravity residuals of about 40 μGal (Fig. 3c box I; Fig. 4) accompanied by slight height changes of 4 cm (Fig. 2a and 4) observed during the first recharging phase. This implies the arrival of a fresh magma volume of about 17 × 106 m3.
Ellipsoidal sources at constant volume (equivalent to a sphere with radius of 1 km) and with different aspect ratios e between the major and minor axes ranging from 0.2 to 2 (prolate ellipsoid e > 1; sphere e = 1; oblate ellipsoid e < 1) are considered (see Methods). The Δg and Δh values for an aspect ratio of about 1.6 is in general agreement with the data (red dots) observed during the 1997 recharging phase (Fig. 3c, box I).
South Rift magma intrusions
The second process is linked to the South Rift dynamic along which magma preferably ascends and intrudes at shallow depth triggering eruptions and fissures propagations32. It is related to the magma injection and withdrawal in a region recognized to be a preferential pathway of magma rising and a favored intermediate accumulation storage at a depth of 3–5 km b.s.l. in proximity of the western border of the high-density and high-velocity body detected by gravity prospecting33 and seismic tomography34. In the South Rift area (from IF to MS gravity stations; Fig. 1) the gravity and deformation patterns changed drastically since 2002, when gravity and height changes were accompanied by a marked horizontal deformation (Fig. 2b). The magmatic intrusions in the South Rift during the 2001 and 2002–2003 eruptions35,36 pushed the volcano flank apart causing a deformation pattern typical of tensile mechanisms with subsidence in the intrusive area and uplift in the zone surrounding the intrusion37. In agreement with the deformation pattern, also the gravity changes are a fingerprint of the activation of the rift area, displaying across the profile negative variations in the central area bounded by positive variations (Fig. 3). Although changes in the gravity field are generally interpreted only in terms of mass input, numerical models38,37 show that for shallow intrusive sources the predominant gravity contribution originates from the displacement of density boundaries. In such a case also the gravity changes display the distinctive tensile pattern that is strongly different from the concentric pattern due to the contribution of mass input alone31,37. This tensile pattern persisted over the following years in the South Rift area showing an extensional behavior, consistent with a regional control on the short-term activity of the volcano39,40. The negative gravity and height changes in the South Rift area slowed down in late-2009, when the third positive gravity cycle started (Fig. 2a and 3c, RS-TG-VE stations). The high gradient in the horizontal deformation maps indicates the South Rift area as a main border of the sliding eastern flank17, which greatly accelerated after the 2002–2003 eruption.
Eastern flank sliding
The third process is concerned with the predominant eastern flank sliding of Mt Etna, whose dynamic markedly affects the deformation and gravity signals. Clear jumps in the deformation and gravity changes are recognized around active faults crossing the profile, reflecting their relative motions and density discontinuity surfaces. After the 2002–2003 eruption the eastern flank accelerated its seaward sliding with an exceptional horizontal deformation accompanied by vertical changes reaching about −10 cm in the easternmost stations17. High gradients are observed in correspondence to CV and FV stations, which are located across the border of one of the main sliding rigid blocks (Fig. 1). The horizontal deformation shows a spatial step more than 20 cm and the gravity changes reverse in sign with a step of about 50 μGal. Although with a smaller gradient, another clear discontinuity in the ground deformation and gravity changes is detected in the western flank between the CC and CE stations, which could be attributed to the dynamics of the Ragalna Fault System crossing the profile (Fig. 1), whose creep movement increased after the 2002–2003 eruption. In the eastern flank the strongest decrease in the gravity signal started in the 2002 and is accompanied in space and time by a significant horizontal deformation (−38 cm), which is about three times larger than that on the western flank. It is worth noting that the gravity decreases faded out as the horizontal deformation ceased. The short wavelengths of the gravity and deformation fields are indicative of shallow and local sources. In this period, this area was also affected by a significant increase in the shallow seismicity (above 5 km bsl14) associated with movement along the faults that border the sliding blocks of the unstable eastern flank. Concurrently, one of the most significant CO2 emissions has been recorded here by geochemical prospecting41. The intense seismicity could have promoted rock fracture and opening of new voids contributing to density decreases and favoring also gas release41. Density variations related to dilation or contraction of the medium can be reasonably attributed to stress-induced variations in crack porosity ϕ, which accompany seismic activity. Fault zone porosity is expected to change during co-seismic processes due to the formation of new cracks, changes from ineffective (or isolated) to effective (or connected) porosity (rearrangement of the interconnection chains between existing voids), grain size comminution, and gouge evolution42. Assuming average values of basaltic rock density33 ρ0 (2400–2600 kg/m3) and reasonable porosity change values Δϕ (0.003–0.006)42, a negative density change Δρ = ρ0Δϕ of about 7–15 kg/m3 is estimated. Considering such a density decrease within the volume releasing most of the seismic energy after the 2002–2003 eruption, the expected gravity change matches quite well the observed variations along the profile in 2004 (Fig. 6), when the maximum negative change of about 70 μGal is obtained at the gravity stations crossing the eastern region.
The gravity source is modeled by a density decrease of 10 kg/m3 within a rectangular prism55 (width = 1 km, height = 3 km, length = 5 km; red dashed rectangle), covering the volume that released most of the seismic energy after the 2002–2003 eruption. (a) Seismic event distributions from 2003 to 2005 (black circles) in the area covered by the gravity stations (green triangles). (b) West-East section showing the distribution with depth of the seismicity. (c) Computed (blue line) and observed (red line) gravity changes along the profile. Geographical coordinates are expressed in UTM projection, zone 33 N.
Discussion
Focusing on the spatiotemporal evolution of the vertical and horizontal ground deformation as well as of gravity changes, we shed light on the complex interplay among the main processes controlling the Etna dynamics. In particular, our analysis draws out: (i) unusual large and positive values of the gravity and height change ratio, (ii) a clear influence of the volcano structural setting on both deformation and gravity patterns, and (iii) a complex relationship between volcanic and tectonic processes. Since different mechanisms are involved and overlapped, they likely mask their effects with each other, and make it difficult to find a general and simple relationship between gravity and deformation, as usually occurs in closed volcanic systems5.
The analysis of long-period microgravity and DInSAR observations has highlighted, over the last 16 years, a clear signature of the South Rift activity, which shows a tensile pattern typical of extensive mechanisms, the sliding of the eastern flank of the volcanic edifice, which leads to large horizontal displacements and negative gravity changes attributed to an increase in void and crack growth, and some magma charging phases, which result in moderate uplift and cyclic gravity changes. During the main recharging phases, the ratio between gravity and height variations is indicative of an overall mass increase within the volcano with limited ground deformation (Fig. 4), pointing out a poor interaction between the intermediate storage system (2–4 km depth) and the arrival of fresh magma. This suggests that the magma should be highly compressible and rich in volatiles. In fact, recharging phases have been accompanied with high SO2 flux emissions, preceding paroxysm activity and fire fountaining episodes22, in which the gas-rich magma, supplied from intermediate feeding system, propels the lava fountains, following a foam collapse model43,44. The cyclic changes in microgravity could arise from the formation of magma batches in the magma storage region resulting from the convective overturn of shallow degassed and denser magma that is replaced periodically by lower density, gas-rich magma from depth. The convective overturn and recycling, at possibly quite low rate, of magma supplying fresh gas-rich melts is a continuous source of volatiles45 and is recognized to promote intense eruptive cycles at Etna46.
The combined gravity and DInSAR observations provide the signature of recharging phases within the volcano in 1997 and 2001 as well as in 2011, which preceded and accompanied the onset of intense flank eruptions and lava fountaining activity at summit craters (Fig. 3d). Actually, the last magma charging phase preceded by a few months the renewal of the Etna eruptive activity, characterized by 38 episodes of short-lived and high intensity lava fountains from the South-East Crater between 2011 and 2013 (at the time of writing). The quality and quantity of DInSAR data available in terms of spatial and temporal resolution allowed not only capture of the deformation pattern but also interpretation of microgravity changes to detect possible magma rising in months to years before the onset of a new Etna eruption. Ultimately, using complementary gravity and DInSAR data will help move us toward a realistic forecasting of eruptions, which comes from a better understanding of processes happening within a volcano edifice.
Methods
DInSAR measurements
Along the West-East profile we generated a first time series obtained from a data set composed of 132 descending and 155 ascending orbit SAR images, acquired by ERS/ENVISAT satellites (from 1995 to 2009); a second time series was generated by using 119 descending and 121 ascending images acquired by COSMO-SkyMed (CSK) satellites (from 2009 to 2011). In the 2000–2003 period, DInSAR data became discontinuous because of the unavailability of two out of three satellites (ERS1 mission terminated in 2000, ENVISAT began in March 2002) while a gyroscope failure on the remaining satellite (ERS2) occurred in January 2001 and was not recovered until late 2001 when the satellite attitude was again put within the specifications47. The satellite data were processed using the Small Baseline Subset (SBAS) algorithm48, which allows us to detect surface displacements and analyze their temporal evolution by generating deformation time series projected along the radar line of sight (LOS). The LOS ascending and descending deformation time series were subsequently combined to resolve for vertical and horizontal (east-west) displacements. Since for this site the data were acquired quite regularly from both orbits, each ascending acquisition could be combined to a corresponding descending one acquired a few days later17. The obtained vertical and horizontal time series relevant to the 1995–2009 and 2009–2011 time intervals were finally connected by using a continuity criterion, thanks to the higher temporal resolution of CSK data.
Among the obtained deformation time series, we selected those pertinent to coherent SAR pixels that were the closest to each gravity benchmark (the distance between the SAR pixels and the corresponding gravity benchmark ranges from 21 to 700 m for the ERS/ENVISAT series and from 8 to 300 m for the higher resolution CSK data, Fig. 1). Figure 2 shows the horizontal and vertical deformation measured in the West-East profile stations between June 1995 and December 2011. The SBAS time series accuracy is assumed to be less than 1 cm, in accordance with previous studies49. The vertical deformation ranges between −20 cm and 6 cm associated with a horizontal deformation from −13 cm to 38 cm (eastward motion is represented by positive values) over the whole considered period. The most significant displacements are detected starting from 2002 and affect the middle and the eastern part of the profile. In particular, the largest height displacement reached about −20 cm around 2008 in proximity to the TG gravity station, in the middle part of the profile; on the other hand, the maximum amplitude in horizontal displacements (38 cm) is located in correspondence to the CV, FV and MO gravity stations on the eastern side of the profile.
Gravity measurements
Microgravity measurements were conducted along the West-East profile by the "step method"14,50, thus each pair of adjacent stations are connected at least three times in order to monitor continuously instrumental performance. Since its installation (summer of 1994), 121 surveys were carried out quasi-monthly until December 2011 using the Scintrex CG-3M gravimeter (serial # 9310234), which is periodically calibrated along the Catania – Etna absolute-calibration-line15.
All measurements were then referred to the westernmost station of the profile (ADR, Fig. 1), since it is the least likely station to be affected by temporal gravity changes14. The uncertainty in gravity measurements, collected with the Scintrex CG-3M gravimeter, ranges, on average, between ± 7 and ± 11 μGal at the 95 percent confidence interval14. Fig. 3a shows the gravity variations measured in the West-East profile stations from June 1995 to December 2011. To interpret the gravity changes over time, it is necessary to reduce the gravity data for the free-air effect, seasonal variations and several high-frequency disturbances51,14. The observed gravity data were firstly corrected for elevation changes using the DInSAR derived vertical deformation (Fig. 2a) and the theoretical vertical gravity gradient (−3.086 μGal/cm). Vertical uplifts, evaluated by DInSAR time series during the entire period, show large variations able to induce significant gravity changes. Moreover, the high gradient along the profile in the vertical deformation addresses that free-air contributions must be estimated at each station to perform accurate corrections. Thanks to the high spatial resolution and the good accuracy, DInSAR derived height changes could fill the lack of GPS measurements at each gravity station. In Fig. 3b the corrected free-air gravity changes are shown. Free-air corrections do not significantly modify the spatiotemporal gravity map until 2007 (Figs. 3a–b). Afterwards, important free-air contributions are estimated. Particularly, positive gravity changes recorded since 2007 in the easternmost stations fade out after the correction, while in the central and western parts the positive changes are reduced and the negative ones are enhanced as a result of the negative height changes recorded in this area after 2002–2003 (Fig. 2a). The free-air contribution is remarkable in the middle sector of the profile at the TG gravity station in proximity of the South Rift, where a maximum value of about 60 μGal was estimated in correspondence to the largest height changes (−20 cm, Fig. 2a). The free-air corrected gravity map was then filtered using a 2-D wavelet multi-resolution analysis14 to reduce the high frequency variations, related to human and environmental disturbances, and the seasonal fluctuations, mainly due to water-table fluctuations, and to highlight the useful signals (i.e. the volcano-related one). Figure 3c shows the residual spatiotemporal gravity map, where both significant positive and negative gravity changes are observed in the analyzed period.
Gravity-height changes
The ratio between gravity and elevation changes for a spherical chamber charged with incompressible magma, after the free-air correction, is proportional to the magma density ρm as  , where G is the universal gravitational constant52. If the magma is considered compressible, after some algebra following Bonafede and Ferrari26, the Δg/Δh ratio is modified as
, where G is the universal gravitational constant52. If the magma is considered compressible, after some algebra following Bonafede and Ferrari26, the Δg/Δh ratio is modified as  , where μ is the rigidity of the surrounding rock and χ the magma compressibility controlled by magma chamber conditions (i.e., pressure, gas volume fraction, phenocryst content, and temperature). Magma compressibility is very small for a gas-free magma (0.04–0.2 GPa−1)27 but relatively large if volatiles exsolve, reaching, for basaltic magma, 10 GPa−1 depending on depth28, or even more for felsic magma. Considering average values of medium rigidity (0.1–30 GPa), the term
, where μ is the rigidity of the surrounding rock and χ the magma compressibility controlled by magma chamber conditions (i.e., pressure, gas volume fraction, phenocryst content, and temperature). Magma compressibility is very small for a gas-free magma (0.04–0.2 GPa−1)27 but relatively large if volatiles exsolve, reaching, for basaltic magma, 10 GPa−1 depending on depth28, or even more for felsic magma. Considering average values of medium rigidity (0.1–30 GPa), the term  may be relevant28 and range between 1.05 and 9, thus giving a maximum ratio of 6.28 μGal/cm. The Δg/Δh ratio is also affected by the source geometry. While for gravity changes the geometry effect is negligible, for height changes it can strongly affect the solution. At a constant volume, the pressurization of a prolate ellipsoid engenders lower height changes with respect to a spherical source as the aspect ratio increases31. The expected Δg/Δh ratio for ellipsoidal sources at a depth of 3 km with different ellipse aspect ratios from 0.2 to 2 were numerically computed31,53,54, considering also the effect of magma compressibility. The Δg/Δh ratio is larger for prolate ellipsoids and may reach 13 μGal/cm (Fig. 5).
may be relevant28 and range between 1.05 and 9, thus giving a maximum ratio of 6.28 μGal/cm. The Δg/Δh ratio is also affected by the source geometry. While for gravity changes the geometry effect is negligible, for height changes it can strongly affect the solution. At a constant volume, the pressurization of a prolate ellipsoid engenders lower height changes with respect to a spherical source as the aspect ratio increases31. The expected Δg/Δh ratio for ellipsoidal sources at a depth of 3 km with different ellipse aspect ratios from 0.2 to 2 were numerically computed31,53,54, considering also the effect of magma compressibility. The Δg/Δh ratio is larger for prolate ellipsoids and may reach 13 μGal/cm (Fig. 5).
References
Carbone, D., Budetta, G. & Greco, F. Bulk processes prior to the 2001 Mount Etna eruption, highlighted through microgravity studies. J. Geophys. Res. 108, B12, 2556, 10.1029/2003JB002542 (2003).
Currenti, G., Napoli, R. & Del Negro, C. Toward a realistic deformation model of the 2008 magmatic intrusion at Etna from combined DInSAR and GPS observations. Earth Planet. Sc. Lett. 312, 22–27, 10.1016/j.epsl.2011.09.058 (2011).
Battaglia, M., Troise, C., Obrizzo, F., Pingue, F. & De Natale, G. Evidence for fluid migration as the source of deformation at Campi Flegrei caldera (Italy). Geophys. Res. Lett. 33, L01307, 10.1029/2005GL024904 (2006).
Gottsmann, J., Rymer, H. & Berrino, G. Caldera unrest at the Campi Flegrei: A critical evaluation of source parameters from geodetic data inversion. J. Volcanol. Geotherm. Res. 150, 132–145 (2006).
Williams-Jones, G. & Rymer, H. Detecting volcanic eruption precursors: a new method using gravity and deformation measurements. J. Volcanol. Geotherm. Res. 113, 379–389 (2002).
Carbone, D., Budetta, G. & Greco, F. Possible mechanisms of magma redistribution under Mt Etna during the 1994–1999 period detected through microgravity measurements. Geophys. J. Int. 153, 187–200 (2003).
Gottsmann, J. et al. New evidence for the reactivation of Teide volcano. Geophys. Res. Lett. 33, 10.1029/2006GL027523 (2006).
Bonaccorso, A. et al. Magma storage, eruptive activity and flank instability: Inferences from ground deformation and gravity changes during the 1993–2000 recharging of Mt. Etna volcano. J. Volcanol. Geoth. Res. 200, 245–254 (2011).
Gabriel, A. K., Goldstein, R. M. & Zebker, H. A. Mapping small elevation changes over large areas: Differential radar interferometry. J. Geophys. Res. 94, 9183–9191 (1989).
Massonnet, D. et al. The displacement field of the Landers earthquake mapped by radar interferometry. Nature 364, 138–142 (1993).
Sansosti, E., Casu, F., Manzo, M. & Lanari, R. Space-borne radar interferometry techniques for the generation of deformation time series: an advanced tool for Earth's surface displacement analysis. Geophys. Res. Lett. 37, L20305, 10.1029/2010GL044379 (2010).
Solaro, G. et al. SBAS-DInSAR time series in the last eighteen years at Mt. Etna volcano (Italy). 2011 IEEE International Geoscience and Remote Sensing Symposium (IGARSS) 3891–3894, 10.1109/IGARSS.2011.6050081 (2011).
Solaro, G. et al. E. Anatomy of an unstable volcano from InSAR: Multiple processes affecting flank instability at Mt. Etna, 1994–2008. J. Geophys. Res. 115, B10405, 10.1029/2009JB000820 (2010).
Greco, F. et al. Spatiotemporal gravity variations to look deep into the southern flank of Etna volcano. J. Geophys. Res. 115, B11411, 10.1029/2009JB006835 (2010).
Greco, F. et al. Combining relative and absolute gravity measurements to enhance volcano monitoring at Mt Etna (Italy). Bull Volcanol. 74, 1745–1756, 10.1007/s00445-012-0630-0 (2012).
Ruch, J. et al. Detachment depth revealed by rollover deformation: An integrated approach at Mount Etna. Geophys. Res. Lett. 37, L16304, 10.1029/2010GL044131 (2010).
Ruch, J. et al. How do rift zones relate to volcano flank instability? Evidence from collapsing rifts at Etna. Geophys. Res. Lett. 39, L20311, 10.1029/2012GL053683 (2012).
Acocella, V., Behncke, B., Neri, M. & D'Amico, S. Link between major flank slip and eruptions at Mt. Etna (Italy). Geoph. Res. Lett. 30, 24, 2286, 10.1029/2003GL018642 (2003).
Borgia, A., Ferrari, L. & Pasquarè, G. Importance of gravitational spreading in the tectonic and volcanic evolution of Mount Etna. Nature 357, 231–235 (1992).
Rust, D. & Neri, M. The boundaries of large-scale collapse on the flanks of Mount Etna, Sicily. in Volcano Instability on the Earth and Other Planets (eds McGuire, W. J., Jones, A. P. & Neuberg, J.) 193–208 (Geol. Soc. Lond. Spec. Pub., 110 1996).
Bonforte, A., Guglielmino, F., Coltelli, M., Ferretti, A. & Puglisi, G. Structural assessment of Mt. Etna volcano from Permanent Scatterers analysis. Geochem. Geophys. Geosyst. 12, Q02002, 10.1029/2010GC003213 (2011).
Allard, P., Behncke, B., D'Amico, S., Neri, M. & Gambino, S. Mount Etna 1993–2005: Anatomy of an evolving eruptive cycle. Earth Sci. Rev. 78, 85–114 (2006).
Lundgren, P. et al. Coupled magma chamber inflation and sector collapse slip observed with synthetic aperture radar interferometry on Mt. Etna volcano. J. Geophys. Res. 108, 2247, 10.1029/2001JB000657 (2003).
Lanari, R., Lundgren, P. & Sansosti, E. Dynamic deformation of Etna volcano observed by satellite radar interferometry. Geophys. Res. Lett. 25, 10, 1541–1544, 10.1029/98GL00642 (1998).
Carbone, D., Currenti, G. & Del Negro, C. Elastic model for the gravity and elevation changes before the 2001 eruption of Etna volcano. Bull. Volcanol. 69, 553–562, 10.1007/s00445-006-0090-5 (2007).
Bonafede, M. & Ferrari, C. Analytical models of deformation and residual gravity changes due to a Mogi source in a viscoelastic medium. Tectonophysics 471, 4–13 (2009).
Spera, F. J. Physical properties of magmas. in Encyclopedia of Volcanoes (ed Sigurdsson, H.) 171–190 (Elsevier, New York, 2000).
Rivalta, E. & Segall, P. Magma compressibility and the missing source for some dike intrusions. Geophys. Res. Lett. 35, L04306, 10.1029/2007GL032521 (2008).
Bonforte, A., Bonaccorso, A., Guglielmino, F., Palano, M. & Puglisi, G. Feeding system and magma storage beneath Mt. Etna as revealed by recent inflation/deflation cycles. J. Geophys. Res. 113, B05406, 10.1029/2007JB005334 (2008).
Huppert, H. E. & Woods, A. W. The role of volatiles in magma chamber dynamics. Nature 420, 493–495 (2002).
Currenti, G., Del Negro, C. & Ganci, G. Modelling of ground deformation and gravity fields using finite element method: An application to Etna volcano. Geoph. J. Int. 169, 10.111/j.1365–246X.2007.03380.x. (2007).
Cappello, A. et al. Spatial vent opening probability map of Mt Etna volcano (Sicily, Italy). Bull. Volcanol. 74, 2083–2094, 10.1007/s00445-012-0647-4 (2012).
Schiavone, D. & Loddo, M. 3-D density model of Mt. Etna Volcano (Southern Italy). J. Volcanol. Geoth. Res. 164, 161–175 (2007).
Patané, D., De Gori, P., Chiarabba, C. & Bonaccorso, A. Magma ascent and the pressurization of Mount Etna's volcanic system. Science 299, 2061–2063, 10.1126/science.1080653 (2003).
Bonaccorso, A., Currenti, G., Del Negro, C. & Boschi, E. Dike deflection modelling for inferring magma pressure and withdrawal, with application to Etna 2001 case. Earth Planet. Sc. Lett. 293, 121–129, 10.1016/j.epsl.2010.02.030 (2010).
Neri, M. et al. Contrasting triggering mechanisms of the 2001 and 2002–2003 eruptions of Mount Etna (Italy). J. Volcanol. Geotherm. Res. 144, 235–255 (2005).
Currenti, G., Napoli, R., Di Stefano, A., Greco, F. & Del Negro, C. 3D integrated geophysical modeling for the 2008 magma intrusion at Etna: Constraints on rheology and dike overpressure. Phys. Earth Planet. Int. 185, 44–52, 10.1016/j.pepi.2011.01.002 (2011).
Okubo, S. Gravity and Potential Changes due to Shear and Tensile Faults in a Half-Space. J. Geoph. Res. 97(B5), 7137–7144 (1992).
Lanzafame, G., Leonardi, A., Neri, M. & Rust, D. Late overthrust of the Appenine–Maghrebian Chain at the NE periphery of Mt. Etna, Italy. C.R. Acad. Sc. Paris 324(IIa), 325–332 (1997).
Monaco, C. et al. Tectonic control on the eruptive dynamics at Mt. Etna volcano (eastern Sicily) during the 2001 and 2002–2003 eruption. J. Volcanol. Geotherm. Res. 144, 221–233 (2005).
Federico, C., Camarda, M., De Gregorio, S. & Gurrieri, S. Long-term record of CO2 degassing along Mt. Etna's flanks and its relationship with magma dynamics and eastern flank instability. Geochem. Geophys. Geosyst. 12, Q10002, 10.1029/2011GC003601 (2011).
Bizzarri, A. Effects of permeability and porosity evolution on simulated earthquakes. J. Struct. Geol. 38, 243–253, 10.1016/j.jsg.2011.07.009 (2012).
Jaupart, C. & Vergniolle, S. Laboratory models of Hawaiian and Strombolian eruptions. Nature 331, 58–60 (1988).
Bonaccorso, A. et al. From source to surface: Dynamics of Etna's lava fountains investigated by continuous strain, magnetic, ground and satellite thermal data. Bull. Volcanol. 75, 690, 10.1007/s00445-013-0690-9 (2013).
Allard, P. Endogenous magma degassing and storage at Mount Etna. Geophys. Res. Lett. 24, 2219–2222 (1997).
Corsaro, R. A. & Pompilio, M. Buoyancy-controlled eruption of magmas at Mt Etna. Terra Nova 16, 16–22 (2004).
Miranda, N., Rosich, B., Santella, C. & Grion, M. Review of the impact of ERS-2 piloting modes on the sar doppler stability. Proc. of FRINGE 2003 Workshop, Frascati, Italy, 1–5 December 2003 (2004).
Berardino, P., Fornaro, G., Lanari, R. & Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sensing 40, 2375–2383, 10.1109/TGRS.2002.803792 (2002).
Casu, F., Manzo, M. & Lanari, R. A quantitative assessment of the SBAS algorithm performance for surface deformation retrieval from DInSAR data. Remote Sens. Environ. 102, 3–4, pp. 195–210, 10.1016/j.rse.2006.01.023 (2006).
Pistorio, A. et al. High precision gravity measurements using absolute and relative gravimeters at Mount Etna (Sicily, Italy). Annals Geophys. 54, 5, 10.4401/ag-534 (2011).
Battaglia, M. & Hill, D. P. Analytical modeling of gravity changes and crustal deformation at volcanoes: The Long Valley caldera, California, case study. Tectonophysics 471, 45–57, 10.1016/j.tecto.2008.09.040 (2009).
Hagiwara, Y. The Mogi model as a possible cause of the crustal uplift in the eastern part of Izu Peninsula and related gravity change. Bull. Earthq. Res. Inst., Tokyo Univ. 52, 301–309 (1977).
Amoruso, A. & Crescentini, L. Shape and volume change of pressurized ellipsoidal cavities from deformation and seismic data. J. Geophys. Res. 114, B02210, 10.1029/2008JB005946 (2009).
Currenti, G., Del Negro, C. & Ganci, G. Finite element modeling of ground deformation and gravity field at Mt. Etna. Annals Geophys. 51, 1, 105–119 (2008).
Blakely, R. J. Potential Theory in Gravity and Magnetic Applications (Cambridge Univ. Press, New York, 1995).
Acknowledgements
This work has been partially supported by Italian Space Agency (ASI) within the SAR4Volcanoes project, agreement n. I/034/11/0. The authors are also indebted to the staff of INGV-Catania, who ensured the regular working of the gravity network of Etna. The seismic data were extracted from the databases of the VOLUME project (European Commission FP6-2004-Global-3, http://ctwall.ct.ingv.it/volume/index.asp).
Author information
Authors and Affiliations
Contributions
C.D.N., G.C. and E.S. coordinated the writing of the paper and the research it is based on; DInSAR processing and analysis were undertaken by G.S., A.P., S.P. and F.C.; gravity measurements were carried out and analyzed by F.G. with the contribution of R.N.; G.C. assisted in data processing and performed numerical modeling.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Negro, C., Currenti, G., Solaro, G. et al. Capturing the fingerprint of Etna volcano activity in gravity and satellite radar data. Sci Rep 3, 3089 (2013). https://doi.org/10.1038/srep03089
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03089
This article is cited by
-
A long-term charge/discharge cycle at Mt. Etna volcano revealed through absolute gravity and GPS measurements
Journal of Geodesy (2022)
-
Characterization of the response of spring-based relative gravimeters during paroxysmal eruptions at Etna volcano
Earth, Planets and Space (2014)
-
Lava flow hazards at Mount Etna: constraints imposed by eruptive history and numerical simulations
Scientific Reports (2013)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.