Introduction

The interlayer cohesive properties in graphite have been an attractive issue for more than 50 years1,2,3,4,5,6,7,8,9, and revive these years due to the observation of graphene and few-layer graphite10,11,12. Although there exist AB and ABC stackings of graphite in nature, a stable single crystal specimen can be well prepared only for AB-stacked graphite13,14,15. This fact has greatly hindered the research on layer-related properties of graphite and as a result, the overwhelming majority of theoretical efforts have been devoted only to AB-stacked graphite5,6,7,9. Actually, it is a physical challenge to theoretically describe the van der Waals (vdW) interactions in complex materials, and extensive work is still needed for better understanding the interlayer cohesion in graphite both theoretically and experimentally. However, as will be shown in this work, the interlayer binding energies in graphites with various stackings are closely related. Therefore, instead of focusing on only one type of stackings, the present work combines both AB- and ABC-stacked graphites to study interlayer potentials in graphite or graphene-graphene interactions, which can be extracted by combining ab initio calculations with Chen-Möbius inversion16,17,18, and further be employed to study layer-related properties of graphite systems over a wide range.

In this work, we use ab initio calculations to generate binding energies of ABC- and AB-stacked graphite as functions of the layer separation. Afterward, the graphene-graphene interaction potentials are obtained using Möbius inversion procedure. Finally, a few examples are given to show the validity and usefulness of the deduced interlayer potentials. These potentials are expected to be powerful in studying graphites with arbitrary c-axis stacking order19 or layer spacings, which can be too large for ab initio calculations, and in understanding even predicting the transformation of stacking orders in multi-layer graphene20. Further by including the variance of lattice parameters, this method can be extended to study strain effects on stacking orders21.

Results

By evaluating values of the equilibrium interlayer distance, d0, the binding energy, Eb, and the elastic coefficient, C33, and making comparison with experimental values as listed in Table I, we find that PBE/DFT-D2 is the best exchange-correlation functional among the functionals that we choose for presenting the ab initio binding energies of graphites. As a verification, we check the asymptotic behavior of interlayer binding energy of AB-stacked graphene. In Fig. 1, we plot the interlayer binding energy of AB-stacked graphite and a fitting by the function y = A/d4.2 + C as a function of the interlayer distance, d. Obviously, the interlayer binding energy curve from PBE/DFT-D2 between 4 ~ 8 Å satisfies the rule very well, which agrees with previous finding using random phase approximation in AB-stacked graphite6,22. What is more, we note that the PBE/DFT-D2 calculated Eb of AB-stacked graphite is greater than that of ABC-stacked one at equilibrium interlayer distance by 0.25 meV/atom, which qualitatively agrees with the estimation of its natural abundance (80%)23.

Table 1 Ab initio equilibrium interlayer distance d0 (in Å), binding energy Eb (in meV/atom), and elastic constant C33 (in GPa) obtained using various exchange-correlation functionals for AA-, AB-, and ABC-stacked graphites
Full size table
Figure 1: Binding energy of AB-stacked graphite as a function of interlayer distance.
figure 1

The PBE/DFT-D2 results are fitted by the function y = A/d4.2 + C, where C and A are coefficients.

Full size image

Despite of four different arrangements along hexagonal close packed (hcp) 〈0001〉 direction, AB, ABC, ABAC, and AA stackings, there are only two different graphene-graphene interaction potentials due to the three-fold rotation symmetry in individual graphene layers. Herein, we use ϕAB(d) to denote the interlayer potentials between A-B, A-C, or B-C layers, and ϕAA(d) those between aligned layers, i.e., A-A, B-B, and C-C layers. Based on the PBE/DFT-D2 results and using a modified Möbius method as will be introduced in the Method section, interlayer potentials ϕAA/AB(d) can be extracted. In Fig. 2, we plot the interlayer potentials ϕAB(d) and ϕAA(d) as functions of d. As shown in the figure, ϕAB(d) takes its minimum value at d0, and ϕAA(d) monotonically increases from d > 5 Å.(Note that ϕAA(d) is plotted only for large interlayer distances, since equations (8) and (9) requires that d ≥ 2d1, where d1 is the minimum interlayer distance we set for ab initio calculation).

Figure 2
figure 2

Interlayer potentials ϕAB(d) and ϕAA(d).

Full size image

So as to better describe the interlayer potentials, we use the Rahaman-Stillinger-Lemberg (RSL2) function

to fit the deduced interlayer potentials. With the total 12 adjustable parameters, ai, bi, ci, (i = 1, 2, 3), this function can well describe pair interactions between layers. The best-fit parameters for the interlayer potentials are listed in Table II.

Table 2 Best-fit parameters for the interlayer potentials using RSL2 function [see equation (1)]
Full size table

From the deduced interlayer potentials ϕAB(d) and ϕAA(d), we can reproduce the interlayer binding energies of variously stacked graphites as:

where the subscript ϕ means that the functions are evaluated from ϕAA/AB(d), instead of directly obtained from ab initio calculations. The reconstructed binding energy curves of AB- and ABC-stacked graphites are plotted and compared in Fig. 3. It is clearly shown in Fig. 3(a) and (b) that the binding energies of AB- and ABC-stacked graphites are well reproduced. Especially, the interlayer binding energy difference between AB- and ABC-stacked graphites is well distinguished in Fig. 3(c). Also, the obtained binding energy curve of AA-stacked graphite shows good consistency with the ab initio results for d ≥ 2d1, where d1 is the minimum d used in ab initio calculations (data not shown).

Figure 3
figure 3

Binding energy curves of (a) AB- and (b) ABC-stacked graphite as functions of interlayer distance. (c) Comparison of binding energies of AB- and ABC-stacked graphites obtained from interlayer potentials near the equilibrium distance.

Full size image

Discussion

Besides giving us more insight into weak interlayer interactions, interlayer potentials are powerful in studying layer-related properties, such as c-axis phonon dispersion, exfoliation energy, cleave energy, surface energy, and stacking fault energy.

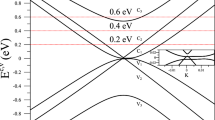
Since interlayer potentials can fully describe the interactions between layers along the hcp 〈0001〉 direction, we can use interlayer potentials to calculate interlayer vibrations. We take a graphene layer as a whole and use the interlayer potentials to describe the graphene-graphene interaction. The phonon dispersion results, which are actually the c-axis vibration spectra, are illustrated in Fig. 4, where the branches of phonon dispersion for AB-stacked graphite are well consistent with those of the neutron scattering data from Ref. 24. In unit of meV, the values of frequency are 17 meV, 1.5 meV, and 0 at the Γ point from the interlayer potentials, which qualitatively agree with the experimental values: 15, 6, and 0 meV24.

Figure 4
figure 4

Phonon dispersion of AB- and ABC-stacked graphites along the c axis.

Full size image

Exfoliation energy, Eexf, is the energy required to remove one graphene plane from the surface of a bulk graphite, and can be used to estimate Eb. With the interlayer potentials, we can easily obtain Eexf. For instance, the exfoliation energy for AB-stacked graphite is followed as:

Compared to equation (2), the Eexf in the above equation is exactly half of the interlayer binding energy. Thereby, the exfoliation energy is about 55.16 meV/atom. Similarly, we can obtain an exfoliation energy 57.14 meV/atom when two graphene layers are exfoliated.

Another method to calculate Eb is to get the cleave energy, Ecl, which is the interaction energy between two semi-infinite crystals. In AB-stacked graphite, it shows that

Apparently, the cleave energy is bigger than the exfoliation energy in AB-stacked graphite. The difference is about 2.3 meV/atom.

The surface energy is defined as the excess free energy per unit area of a particular crystal facet. It is usually calculated using the supercell method: Esurf = (Es − N E0)/2A, where Es is the total energy of the supercell, E0 the bulk energy per layer, A the surface area of the supercell, and the factor 2 derived from two surfaces in the supercell model. Esurf can also be easily computed by interlayer potentials, which yields that the surface energy is about 351 mJ/m2 for AB-stacked graphite. The interlayer potentials may also be used to establish the size of the surface relaxation and the impact on the formation energy. In the present surface relaxation is only between the surface layer and the neighboring layer. The surface relaxation energy from the interlayer potentials is 338 mJ/m2, which is 13 mJ/m2 smaller than the ideal surface energy. The relaxation interlayer distance is about 3.238 Å, while the equilibrium interlayer distance is 3.231 Å. Similarly, we also calculated the surface energy of ABC-stacked graphite along hcp 〈0001〉. Its value is 344 mJ/m2 which is smaller by 7 mJ/m2 than that of AB-stacked graphite. Note that the the surface energy calculated with LDA is only 75 mJ/m2 for AB- stacked graphite as reported in Ref. 25. The large difference is mainly derived from the interlayer cohesive energy of the different exchange-correlation approximations.

Also, commonly seen stacking faults can be studied. We calculate the intrinsic stacked fault energies of AB-stacked graphite according to the equation Esurf = (Esf − Eideal)/Asf. Herein Esf is the energy of the intrinsic stacking fault, Eideal is the energy of the perfect stacking, and Asf is the area of the stacking fault plane.

Ideal stackings are for AB-stacked graphite, for ABC-stacked graphite, for the ABAC-stacked graphite, and for AA-stacked graphite. Herein, we only consider one stacking fault from AB-stacked to AA-, ABC-, and ABAC-stacked graphites. From ABC- to AB-stacked graphite, namely to the stacking fault energy is −8.0 mJ/m2, which also indicates that AB-stacked graphite is more stable than ABC-stacked one. From AB- to AA-stacked graphite, to the stacking fault energy is 148 mJ/m2. From AB- to ABAC-stacked graphite, to , the stacking fault energy is 7.9 mJ/m2, which implies that the interlayer binding energy of ABC-stacked graphite is very close to that of ABAC-stacked graphite.

In summary, we have obtained interlayer potentials ϕAB/AA(d) combining the Möbius inversion method with ab initio results. The interlayer potentials can well reproduce binding energies of graphites with AB or ABC stackings, indicating the validity of the interlayer potentials, and can be used to predict many properties such as c-axis phonon dispersion, exfoliation energy, surface energy, surface relaxation, and stacking fault energies of various graphites. We conclude that the interlayer potentials offer an easy and efficient way to investigate layer-related properties of graphites, and the combination of Möbius inversion method and ab initio calculation may find wide applications in layered structures.

Methods

There exist numerous ab initio calculation methods with different exchange-correlation approximations to deal with the vdW interaction. However, it is still difficult to exactly include the nonlocal long-range vdW interaction. In the present work, we have tested seven different exchange-correlation functionals (see Table I)26,27,28,29. Considering only the interaction between layers, we fix the interatomic distance within each layer and obtain the corresponding total energy at different interlayer distances by changing the interlayer distance. After extracting the sum of energies of individual layers from the total energy, we get the interlayer binding energy as a function of interlayer distance. All ab initio calculations have been performed within the Vienna Ab initio Simulation Package (VASP)30,31. To take into account the small energy change caused by the weak vdW interaction, the cutoff energy is taken as 900 eV, the k mesh in the first Brillouin zone is set to be 16 × 16 × 12, and the convergence of total energy is 2 × 10−7 eV. In order to better describe the graphene-graphene interaction in graphite, we need to select the best exchange-correlation functional for the system for further analysis. As usually done in literature, we use the consistency of calculated results to the experimental values of equilibrium interlayer distance d0, the binding energy Eb, and the elastic coefficient C33, as the criteria. The Morse function32 is chosen as the state function to fit the binding energy values near the ideal interlayer distance to get d0, Eb, and C33.

In our calculations, the interlayer binding energy is defined as the atom-averaged energy difference between separated layers and bound layers as:

where Eb represents the interlayer binding energy in unit of meV/atom, Etot is the total energy of N layers in the calculational model, Eunit corresponds to the energy of a single layer, i.e., graphene, and Natom is the number of atoms per layer. While, the elastic coefficient C33, which is along hcp 〈0001〉 direction in hexagonal lattice, is defined as:

with

where d0 is the equilibrium interlayer distance, and a0 = 1.42 Å is the interatomic distance within a layer.

Given the ab initio results of binding energy functions for AB- and ABC-stacked graphites, we can use the Möbius inversion method to generate interlayer potentials, or graphene-graphene interaction potentials.

In the following, we use Möbius inversion method to get the interlayer potentials from binding energies of AB- and ABC-stacked graphites.

For AB-stacked graphite, the interlayer binding energy EAB(d) is given as

For ABC-stacked graphite, the binding energy can be expressed similarly as

Assuming that EABC(d) and EAB(d) are known, we can combine the equations (8) and (9) to determine ϕAB(d) and ϕAA(d). Introducing the energy difference ΔAB(d) as

we obtain the following formula:

This equation can be written in a simple form:

by introducing ()

The idea of solution is simply to work with the multiplicative closure of the original set , i.e., B is a multiplicative semi-group containing the elements of b, and all products of them16. Correspondingly, the set is extended to another set as

where R(n) satisfies

In the above notation, b−1 refers to the inverse of the arithmetic function b(n), i.e., a mapping from the set back to the natural numbers. Similarly to the traditional Möbius inversion method, we can write down a symmetric form as a solution of ϕAB(d):

and substitute it into equation (14) to determine J(n):

from which J(n) can be obtained recursively.

In order to solve ϕAA(d), we define

and then from equation (8), we have

Then, by virtue of Möbius theorem, ϕAA(d) can be obtained as:

where μ(n) is the Möbius function defined as:

Apparently, the interlayer interactions can be strictly considered up to arbitrary-distance neighboring layers on the bases of the above Chen-Möbius inversion method. According to equations (16) and (19), the premise condition of getting ϕAB(d) and ϕAA(d) is to obtain the interlayer binding energies, EABC(d) and EAB(d). Note that as a consequence, the reliability of interlayer potentials depends on the accuracy of interlayer binding energies, and besides ab initio calculations, experimental binding energy curves, can also be used to generate interlayer potentials.