Introduction

Shor's prime factoring algorithm1 reduces the factorization of a product N = pp′ of distinct odd primes p and p′ to that of finding the order r of a mod N for a randomly chosen base a coprime to N (with 1 < a < N), which can be performed efficiently with a quantum computer. The standard implementation2 factors a b-bit number with 3b qubits using a circuit of depth O(b3); alternative modular exponentiation circuits can be used to reduce either the space (qubit number)3 or time4 requirements. The case N = 15, which has the simplifying property that all orders are powers of 2, has been demonstrated experimentally by several groups2,5,6,7,8. Recent experiments have also factored N = 219,10 and 12811.

In this paper we consider the application of Shor's algorithm to products of special primes of the form

Explicitly,

Fermat proposed that numbers of the form for any k = 0, 1, 2, …, (called Fermat numbers) are prime; however it is now known that the Fermat numbers with 5 ≤ k ≤ 32 are not prime and it is not known whether there are additional primes of this form for larger values of k.

Products of the form

have the special property that the order of a mod N for every base a coprime to N is a power of 2. This follows from Euler's theorem,

where y is a positive integer, ϕ(y) is the number of positive integers less than y that are coprime to y and gcd(a, y) = 1. When p and p′ are odd primes, all pp′ − 1 positive integers less than pp′ are coprime to pp′ except for the p − 1 multiples of p′ and the p′ − 1 multiples of p and these exceptions are distinct, so

(This result also follows from Euler's product formula.) Thus,

Recall that the order r of a mod N is the smallest positive integer x satisfying ax mod N = 1; therefore for a composite of the form (3),

must be a multiple of r. Because r must be an integer, we conclude that for any 1 < a < N with gcd(a, N) = 1, r is a power of 2 as well.

Results

The standard2 order-finding circuit is shown in Fig. 1. The first register has n qubits and the second has m. The modular exponentiation operator in Fig. 1 acts on computational basis states as

where

After the inverse quantum Fourier transform, measurement of the first register is done in the diagonal basis. The probability to observe the value

is

where r is the order and A is the number of distinct values of x such that ax mod N has the same value (this is approximately 2n/r). This probability distribution has peaks at integer values of x near

The number of qubits n in the first register is chosen to enable reliable extraction of the value of r in (12), which depends on whether or not r is a power of 2. In actual applications of Shor's algorithm this will not be known, of course, as the point of the quantum algorithm is to determine r. In this usual situation, measurement will yield (with prob > 4/π2) an x satisfying

By choosing n = 2b qubits in the first register, where b ≡ log2 N, we are guaranteed that j/r will be a (continued fraction) convergent of x/2n. However, for the family of composites considered here, all bases have orders

where the value of ℓmax is discussed below. In this case

and the peaks (12) in (11) occur at integral values

Therefore, as long as we have

qubits in the first register we will be able to determine r, possibly after a small number of repetitions. The simplest way to extract r from x here (assuming x ≠ 0) is to simplify the ratio

down to an irreducible fraction, which will yield both j and r [recall (12)] unless they have happen to have a common factor.

Figure 1
figure 1

Basic quantum circuit for order finding.

Here n = 2b and m = b, where b ≡ log2 N is the number of bits in N.

Full size image

Next we discuss the value of ℓmax (which determines the largest order ) for a given composite N. We do not have an explicit formula for ℓmax. However, when N is a product of distinct odd primes, r can be as large as ϕ(N)/2 (ref. 12), so for an N of the form (3) we have the bound [see (7)]

For example, in the case of N = 51 (k = 0, k′ = 2), the largest order is 24 = 16 and the upper bound is realized. However for N = 85 (k = 1, k′ = 2), it is not (the largest order present is 16, not 32).

The second register stores the values of

and therefore normally requires b qubits. However, for a given a, only r of these values are distinct. Thus we can use fewer than b qubits. This simplification, while not essential, has been used in all gate-based factoring demonstrations to date. The reduction amounts to computing a table of values of ax mod N classically for a given base a, constructing a corresponding quantum circuit and ignoring or eliminating unused qubits in the second register. We note that in addition to being unscalable, this method of constructing the modular exponentiation operator implicitly or explicitly uses the value of the order r, i.e., the answer which the quantum computation is supposed to determine; we discuss this issue further below.

In this work we will adopt an equivalent—but perhaps more systematic and transparent—modular exponentiation circuit construction: We follow the output of ax mod N by a second transformation

which maps the r distinct values of ax mod N to 0, 1, …, r − 1. In (21) we assume that 1 < a < N. We refer to this classical pre-processing of ax mod N as compression. Compression does not adversely affect the operation of the order-finding circuit, but reduces m from b to ℓmax in a systematic manner (and generalizes the “full compilation” method used in Ref. 6.)

Any set of r distinct non-negative integers—in any order—could be used for the output of the compression map (21). However the choice employed here and indicated in (21), is especially simple because it can be compactly written as

Then, after changing the initial state of the second register from to , we have, instead of (8), the compressed modular exponentiation operation

The operation (23) without the modulo r is just the bit-wise COPY shown in Fig. 2 and the effect of the modulo r is to only copy the log2 r least significant bits.

Figure 2
figure 2

Circuit to copy the first register to the second.

Full size image

In conclusion, we require ℓmax qubits in each register, for a total of 2ℓmax qubits. ℓmax can either be computed classically or the bound (19) can be used. We note that the space requirements can be further reduced by using iterative phase estimation13,14,15, but with an increase in circuit depth. This might be useful for ion-trap and optical realizations but probably not for superconducting qubits.

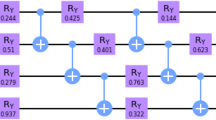
We provide explicit quantum circuits for the cases of N = 51 and 85. In both cases ℓmax = 4 (the largest order is 16), so we require n = 4 qubits in the first register and m = 4 in the second, for a total of 8 qubits. This is significantly fewer than the 3b required for general b-bit numbers (b = 6 when N = 51 and b = 7 when N = 85). It is also fewer than the 2b + 3 qubits required by Beauregard3.

After the compression discussed above, only four different circuits are needed to cover all N = 51 and N = 85 cases, because there are four possible orders. The assignments are listed in Tables I and II and the circuits are given in Figs. 3a–d.

Table 1 N = 51 quantum circuits. The base marked by an asterisk satisfies ar/2 = −1 mod N and will result in a factorization failure in the classical post-processing analysis
Full size table
Table 2 N = 85 quantum circuits. Bases marked by an asterisk satisfy ar/2 = −1 mod N and result in factorization failures in the classical post-processing analysis
Full size table
Figure 3
figure 3

Quantum circuits for factoring 51 and 85.

Note the modification of the input to the last qubit of the second register compared with Fig. 1. The circuits inside dashed boxes are the compressed modular exponentiation operations discussed in the text. Note that the CNOT gates here can be executed in parallel.

Full size image

Circuits for the remaining composites 771, …, 16843009 follow from the method described above and require no more than 2ℓmax qubits. From (19) we find that the total number of qubits required in these cases is bounded by

Discussion

Given the considerable interest in experimental demonstrations of Shor's algorithm, it is reasonable to ask what constitutes a “genuine” demonstration of this important algorithm and whether the cases presented here should be considered as such. In our opinion a genuine implementation should use no knowledge of the value of the order r—including whether or not it is a power of two—because the objective of the quantum stage of the algorithm is to calculate r. Therefore we do not regard the factorization of products of Fermat primes to be genuine implementations of Shor's algorithm. Moreover, such special cases can be efficiently factored classically, by comparing N against a list of products of these primes.

However we do view the circuits presented here as quasi-legitimate implementations of quantum order finding and in our view they are still interesting for this reason. In particular, each eight-qubit circuit presented here is able to detect periods of two, four, eight and sixteen, so there are failure modes where an incorrect period could be observed. But these genuine order-finding instances are nongeneric cases from the perspective of Shor's algorthm. Note that in this work we have simplified the modular exponentiation circuits to reduce their depth. It is also possible to implement uncompiled versions, which do not make any use of the value of r and which would constitute a fully genuine implementation of order-finding (but not of factoring). The main point of this work, that the number of qubits required in the first register is greatly reduced for composites in the series (3), applies to either approach.

Smolin, Smith and Vargo16 recently addressed the question of what should constitute a genuine factoring demonstration by simplifying the entire order-finding circuit for any product of distinct odd primes down to only two qubits. This is possible by implementing the phase estimation iteratively13,14,15 (or the Fourier transform semiclassically17) and by choosing only bases a with order two. Smolin et al.16 show that with knowledge of the factors, it is always possible to find an order-two base and they provide an algorithm for doing so. The circuit of Smolin et al. does not constitute a genuine implementation of Shor's algorithm either. However, the focus of our work is different than that of Ref. 16, as the circuits presented here are still quasi-legitimate implementations of order finding and we do not make explicit use of the factors in simplifying the circuits.

Finally, we note that the r = 16 cases (Fig. 3d) result in a uniform probability distribution for observing computational basis states |x〉 after measurement of the first register, which would also result from an unintended, purely decohering action of the CNOT gates (we thank Alexander Korotkov for this observation). One method of verifying that the circuit is functioning correctly is to perform tomography on the final state. A simpler method, however, is to change the input of the second register from to , as shown in Fig. 4. If the gates are purely decohering, this will not change the output of the first register upon measurement. But if the CNOTs are acting ideally, the entire compressed modular exponentation operator now acts as the identity [because |+〉 ≡ 2−1/2(|0〉 + |1〉) is an eigenvector of the NOT gate] and can be effectively dropped from the circuit, leading to an observation of the final state |0000〉 with unit probability.

Figure 4
figure 4

Changing the input states on the second register to verify coherent operation of the CNOT gates.

Full size image

In conclusion, we have shown that the simple and well-studied case of factoring N = 15 is the first in a series of cases

that have all orders equal to a power of two and that can be factored with fewer resources than that of other products with the same number of bits.

Methods

The results in Tables I and II are found by classically computing the orders r for all bases 1 < a < N satisfying gcd(a, N) = 1. Cases where ar/2 = −1 mod N lead to a failure of Shor's algorithms and are marked by an asterisk. The operation (23) is then implemented by a quantum circuit as described above.