Abstract
Cortical bone, found in the central part of long bones like femur, is known to adapt to local mechanical stresses. This adaptation has been linked exclusively with Haversian remodelling involving bone resorption and formation of secondary osteons. Compared to primary/plexiform bone, the Haversian bone has lower stiffness, fatigue strength and fracture toughness, raising the question why nature prefers an adaptation that is detrimental to bone's primary function of bearing mechanical stresses. Here, we show that in the goat femur, Haversian remodelling occurs only at locations of high compressive stresses. At locations corresponding to high tensile stresses, we observe a microstructure that is non-Haversian. Compared with primary/plexiform bone, this microstructure's mineralisation is significantly higher with a distinctly different spatial pattern. Thus, the Haversian structure is an adaptation only to high compressive stresses rendering its inferior tensile properties irrelevant as the regions with high tensile stresses have a non-Haversian, apparently primary microstructure.
Similar content being viewed by others
Introduction
Complexities of mammalian cortical bone as a material are manifold as its primary constituents, collagenous protein and hydroxyapatite mineral crystals, are intricately arranged in a structure with about seven levels of hierarchy1,2. During the bone's growth, at each level of hierarchy, it dynamically senses the environment of a particular anatomical region and adapts to the local functional needs. Therefore, depending on the anatomical site, bone material may have significantly different microstructural features and therefore, different mechanical properties1,2,3,4,5,6,7,8. Understanding the relationship between the mechanical stresses and the microstructure of bone is vital in prediction of effects of aging and disease on mechanical behavior of bone9,10, as input for more realistic computational models on mechanics of bone11,12, in assessment of mechanical compatibility of implants13, for selection of sites for extracting bone grafts14 etc. It also provides a basis for palaeontologists and anthropologists to infer the functional and behavioral patterns of animals from their bones15 and for forensic scientists a reasonably reliable method for distinguishing human bone from non-human bone16,17.
To understand the functional morphology and the internal load distribution within a bone, numerous studies have focused on the human femur. Biomechanical models that include muscle and joint contact forces have established that the human femur is primarily under compressive load18,19,20,21 which correlates well with the observed uniform circular cross-section and absence of cortical thickening in the human femur diaphysis22. Similar studies on quadruped mammalian femur show that due to angulation of the joint, the bone develops loads transverse to the femoral axis23,24,25,26 giving rise to significant bending stresses27,28.
Studies on the histology of human cortical bone indicate that like many primates and carnivores, the primary fibrolamellar bone is laid initially but soon gets remodeled into Haversian bone. Interestingly, many other mammalian groups, such as, bovids and cervids retain primary fibrolamellar structure even through their adulthood, with only smaller regions remodeling into Haversian bone29. For instance, two different microstructures exist within the cross section at the mid-diaphysis of adult sheep and bovine femur: the posterior is transversely isotropic with randomly arranged Haversian systems (in the cross-sectional plane), the anterior region has orthotropic plexiform structure with microstructurally distinguishable orthogonal directions6,30,31. The two microstructures have different mechanical properties: the elastic modulus6,32, fracture toughness33,34 and resistance to fatigue crack growth35,36,37 of Haversian bone being lower than that of plexiform bone.
The effect of stress on the Haversian microstructure has been studied in the equine radius, where secondary osteons under compression contain transverse collagen while those formed elsewhere contain longitudinal collagen38,39,40. However, until now, bone adaptation to mechanical stresses has been exclusively linked with Haversian remodelling, thereby implying that adapted bone must have secondary osteons41,42. The inferior mechanical properties of Haversian bone have led researchers to question the hypothesis that Haversian internal remodelling occurs primarily to replace primary bone with bone that is well adapted to bear the mechanical stresses29. Can healthy bone be adapting to mechanical stresses in a self-defeating manner? Here, we re-examine the microstructure-stress relationship and hypothesise that bone, at the microstructural level, adapts very differently to compressive and tensile stresses. The hypothesis is supported by correlating the variations in microstructure of the the cortical bone of a domestic goat's femur along its length with the stress field determined from a simple two-dimensional biomechanical model. At sites under high compression, typical Haversian adaptation occurs with scattered secondary osteons. However, under high tensile stresses, we find a compactly layered, non-Haversian, microstructure that is distinctly different from that of the plexiform bone, observed at low stresses. Finally, we present a detailed statistical analysis that unequivocally quantifies the differences in terms of the extent and spatial pattern of the mineralisation. Based on the results of the statistical analysis a discussion is developed on the present thinking on bone adaptation and its applicability to adaptive response under tensile stresses.
Results
Biomechanical model
We first develop a simplified two dimensional biomechanical model for the stance phase of the gait assuming that the internal forces and moments that develop during the stance phase are representative of the amplitude of the dynamic loads that may cause microstructural adaptation. The sagittal plane is chosen for the analysis as the moments acting in this plane are responsible for stresses at the anterior and posterior sites. We set ground reaction for the hind leg equal to 40% of its body weight (BW ≈ 15 kg) and its direction as vertical during the stance and replace muscle and contact forces at the joints by a statically equivalent net force and net moment acting on joint centers23,26. The line joining the contact point with the ground and the center of the hip joint is approximated to be aligned with the vertical as shown in Fig. 1(a). For the static equilibrium of the hind leg, the net in-plane force at the proximal end of the femur is therefore, of the same magnitude as the reaction force from the ground and is acting vertically downward. As a consequence, the static equilibrium of femur in isolation requires an equal and opposite balancing force and a moment at the distal end as shown in Fig. 1(b). The profile of the axis of the bone is approximated by a fourth order Lagrangian polynomial that passes through the measured transverse coordinates at five different locations along the femur as shown as a dotted line in Fig. 1(b). Even though such an approximation does not account for the finer details of the specific bone, it captures the broad features of the bone-axis profile that do not vary significantly from animal to animal and therefore, are more likely to represent the average stress pattern in the femur of a typical quadruped.
(a) Schematic free body diagram of the hind leg of a goat. (b) Free body diagram of the femur in isolation. The angle θ is taken to be 25.48°. (c) Axial stresses along the normalised length of the femur, where the sections S1 to S8 are as in (d). (d) The different sections S1 to S8 are marked on an image of the femur.
Based on the assumptions of the model stated earlier in the section, the femur is a statically determinate structure and thus, for any cross-section along the length, the equilibrium axial force, shear force and the bending moment can be calculated using Euler-Bernoulli beam theory (see supplementary information for details of calculation). The corresponding axial stress field depends only on the BW, joint angulation and the geometrical details of the femur cross-section and is independent of the constitutive behaviour of the bone material. The material constants such as elastic modulus come into play only in the estimation of deformation characteristics of the femur, which is not the focus of the current study. The axial stresses develop due to the combined effect of compression and bending of the bone and its anatomical variation along the length of the femur at the anterior and posterior regions are shown in Fig. 1(c). Both regions develop stresses of comparable magnitude but of opposite nature: tensile at anterior and compressive at the posterior region, which is a consequence of bending stresses being dominant. The magnitude of stress peaks approximately at section S2 of the histological specimens, while section S7 and S8 have low stress [see Figs. 1(c) and (d) for labelling of sections]. The anatomical variation of axial stresses thus determined is qualitatively similar to the three dimensional finite element model predictions for canine femur28 in the following aspects: the anterior region develops tensile stresses while the posterior is in compression and the peak stresses occur nearer to the distal end while the proximal end has negligible axial stress.
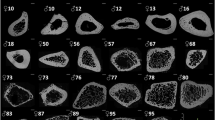
Optical micrographs
We now show that the microstructures are different in regions of high tensile stress (S1–S3 anterior), in regions of low stress (S6–S8 anterior/posterior) and in regions of high compressive stress (S1–S3 posterior), through optical micrographs, back scattered electron detector (BSE) data for mineralisation and energy-dispersive X-ray spectroscopy (EDS) data for calcium content. In the optical micrographs of the different sections shown in Fig. 2, nearer to the proximal end at sections S6–S8, the bone shows similar microstructure at both the anterior and posterior regions. There are layers of woven bone, that is known to have randomly oriented collagen fibrils in the bone matrix conducive for rapid laying of bone, present between layers of primary osteons, typical of fibro-lamellar/plexiform structure29. However, at sections S1–S3 which is approximately at one third bone length from the distal end, within the cross-section there are two distinctly different microstructures present: the posterior region has secondary osteonal growth with random arrangement of the Haversian systems while the anterior region shows compactly layered microstructure with strong banding along the tangential direction. Section S4 also shows differences in microstructure between anterior and posterior sites, though the extent of compaction in anterior and secondary remodelling at the posterior is less in comparison to section S2. By relating the observed microstructure with the stress field obtained from the biomechanical analysis earlier, it is evident that only regions with high compressive stresses have Haversian structure. In regions with low stresses, whether tensile or compressive, the microstructure is the typical fibro-lamellar/plexiform. In the microstructure of the regions with high tensile stresses there is no evidence of Haversian structures or resorption cavities and the lamellae around the osteons merge smoothly with the surrounding bone, typical of primary bone. Interestingly, this apparently primary bone does not have the brick-like structure typical of plexiform bone either.
Mineralisation
To further characterise the apparently primary microstructure found in the regions of high tensile stresses in comparison with the plexiform microstructure of the regions of low tensile stresses, the BSE micrographs of the anterior region of S2 and S7, as shown in Figs. 3(a) and (b), are analysed in detail. From the gray scale data of the BSE images, the spatial pattern of mineralisation is obtained by identifying the spatial location of the brightest 10% pixels such that each data point shown in Figs. 3(c) and (d) corresponds to a region of high mineral content. In section S7, the mineralisation is localised in narrow horizontal bands, with inter-band spacing ℓ* ≈ 135 μm, that span the entire field width and are located approximately at the middle of the woven layers. In contrast, section S2 has much more uniform mineralisation that is evenly spread out with negligible banding. We note that in both the sections there are drying cracks mostly running horizontally through the primary vasculature, while some are oriented vertically, specially in section S7. Many of the cracks have a row of bright pixels contiguous to their boundaries, which is perhaps due to localised charging as, firstly, the curves formed by these row of pixels have exactly the same shape as the crack boundary and secondly, the width of these rows are significantly lower than the width of the highly mineralised bands seen at the central part of the woven layer. Also, the coarse graining of the BSE images show some regions of uniform sparseness, in the left of Fig. 3(d), or denseness, at the top of Fig. 3(c), in the spread of the bright pixels which maybe a result of slight variations in the flatness of the sample surface. Since these artefacts were not obvious in the BSE images during the imaging of the samples, they were harder to avoid.
BSE images of sections (a) S2 anterior and (b) S7 anterior, where the field width is 1475 μm (966 pixels).
The brightest 10% pixels of the BSE images for (c) S2 anterior and (d) S7 anterior. (e) Structure factor S(k) along the direction perpendicular to the banding. Inset: F(z), the probability that the scaled gray scale value is greater than z for S2 and S7. (f) EDS data for calcium content along a line perpendicular to the banding.
The spatial pattern of mineralisation is quantified by studying the structure factor S(k), the Fourier Transform of the two-point correlation function C(y). Here, C(y) = 〈z(xo, yo)z(xo, yo + y)〉, where z is the non-dimensionalised gray scale values obtained by scaling the difference from the mean by the standard deviation, y is the direction perpendicular to the banding and the averaging 〈〉 is done over all spatial points (xo, yo). S(k) for section S7, shown in Fig. 3(e), has a prominent peak at ℓ* ≈ 135 μm, consistent with the inter-band spacing seen in Fig. 3(d). This peak is nearly absent in section S2. More strikingly, the behaviour at large k, corresponding to length scales smaller than a crossover length scale (ξ ≈ 9 μm), representing the transition from one regime to another, is very different for the two sections. For k > ξ−1, S(k) ~ k−2.0 for S7 and S(k) ~ k−0.5 for S2. The k−2.0 behaviour for S7 is the standard Porod law in one dimension43,44 that describes scattering from compact objects with well defined interfaces. For the structure function of S2, the clear deviation from Porod law can be attributed to the absence of well defined mineral-rich, mineral-poor domains45,46. It is to be noted that the cracks are less than 3 μm (2 to 3 pixels) wide and are distributed randomly. Since the structure factor quantifies the periodicity of spatial structure along a single column of pixels, the presence of cracks is not expected to have a significant effect on it. That the statistical characteristics of the mineralisation is independent of the presence of drying cracks is confirmed by identifying comparatively crack free regions of sizes 605 × 401 μm in S2 and 564 × 472 μm in S7 and evaluating the structure factor of the reduced sample size. Other than poorer statistics the structure factor remains unchanged.
In addition to quantifying the spatial pattern of mineralisation, we also characterise the distribution of gray scale values. The probability that the non-dimensionalised gray scale value is larger than z, F(z), is shown in the inset of Fig. 3(e) for S2 and S7. We observe that the tail of the distribution for S7 is distinctly broader suggesting presence of mineral rich and mineral poor regions. Next, the extent of mineralisation in both sections is quantified using EDS line scans along paths orthogonal to the banding. The calcium content obtained from a typical line scan is shown in Fig. 3(f) for both sections. When averaged over six line scans for each section we find the calcium content is 32.3 ± 8.5% higher in S2 than that in S7. The combined evidence shows the presence of a third new microstructure that is non-Haversian and quantifiably different from primary bone. The anatomical location of the new microstructure being at regions with high tensile stresses makes a strong case of it being an adaptation of the bone to high tensile stresses in the local environment.
Discussion
In this paper, a combined histological and biomechanical analysis of the femur of an Indian domestic goat is performed to examine the complex relation between the microstructure and the mechanical stresses in a mammalian cortical bone. We show that, at the microstructural level, adaptation of bone architecture is strongly influenced not just by the magnitude but also by the compressive or tensile nature of the local stress. Haversian remodelling through growth of secondary osteons occurs only in regions under high compressive stresses. In contrast, for high tensile stresses the microstructure is a compactly layered architecture which has no secondary osteonal growth. This apparently primary microstructure not only has on an average 32% higher mineralisation but also the spatial pattern of the mineralisation is quantifiably different from the sparsely layered fibro-lamellar or plexiform structure observed in the low stress region where bone is yet to adapt. Since the Haversian remodelling is shown to be an adaptation only to the compressive stresses in the environment, it cannot be expected to have superior mechanical behavior in tension. This in effect presents a possible solution to the mystery associated with why the adapted Haversian structure has inferior mechanical properties in tension compared to primary bone as reported in several studies.
While the differences in the calcium content between the regions of high tensile stresses and low tensile stresses, as well as in the spatial arrangement of it indicate a strong possibility of differences in the macroscopic properties such as elastic modulus, fracture toughness and fatigue resistance, a detailed study is required to quantify the difference and establish the precise nature of the microstructure-property relation for cortical bone of a goat femur. Such a study is part of just-started projects by the authors but is out of the scope of the present work.
In the present understanding of cortical bone, microstructural adaptation in response to high mechanical stresses is exclusively linked with formation of secondary osteons/Haversian systems. The fact that in the goat's femur, the anterior region near the distal end has high tensile stresses and yet no manifestations of secondary remodelling, raises the question if the present thinking for microstructural adaptation general enough to describe adaptive response of bone under tensile stress? Also, was the apparently primary microstructure of the high tensile stress region initially plexiform which got modified during the goat's life or was it made this way ab initio? These questions are promising areas for further research.
The biomechanical model that we solved shows that bending stresses are strongly dependent on the inclination of the bone to the vertical: expected to disappear for no inclination as in the human femur and have complete reversal in nature of stresses if the bone is inclined to the other side of the vertical, as is the corresponding bone of the foreleg (humerus) of quadrupeds. As per our hypothesised dependence of the microstructure on the nature of the stresses, the anterior of the humerus therefore, should have significant Haversian remodelling. This prediction is well supported by the study on bovine humeral cortical bone which shows dense Haversian microstructure in the anterior quadrant36. Our study therefore explains the reason behind the reported empirical evidence on differences in the microstructure of human and non-human femur which is used as one of the important forensic evidences to distinguish human bone from non-human bone.
Methods
Samples of femur of domestic goats, breed Osmanabadi of Capra hircus that is commonly found in the southern peninsular region of India47, were collected from the local butcher shop within 5 hours of death of the animal (approximately 15 kg in weight and 1.5 years in age). The femurs were stored at −20°C in HBSS soaked gauze and thawed to room temperature before sectioning it using a 0.38 mm hand saw. The specimens were set in PMMA, where sections S2 and S7 were set together in a single PMMA mould to minimise differences in experimental conditions and polished on successively fine grit silicon carbide papers and finally using 1 micron and 0.05 microns alumina suspension to ensure a flat, polished surface.
The optical imaging was performed using a Leitz, Laborlux 12ME optical microscope. BSE imaging was performed using a FEI Quanta 200 SEM mounted with a BSE detector. The images were recorded at 15 kV accelerating voltage and 12.4 mm working distance. EDS line scans were obtained without changing beam characteristics.
References
Qin, Z., Kreplak, L. & Buehler, M. J. Hierarchical structure controls nanomechancial properties of vimentin intermediate filaments. PLoS ONE 4, e7294 (2009).
Launey, M. E., Buehler, M. J. & Ritchie, R. O. On the mechanistic origins of toughness in bone. Annu. Rev. Mater. Res. 40, 25–53 (2010).
Currey, J. D. Mechanical properties of vertebrate hard tissues. Proc. Instn. Mech. Engrs. 212, 399–412 (1998).
Fratzl, P. Biomimetic materials research: what can we really learn from nature's structural materials? J. R. Soc. Interface. 4, 637–642 (2007).
Jeronimidis, G. Structure-property relationships in biological materials., in Elices, M. (Ed.), Structural Biological Materials, Design and Structure-Property Relationships. Pergamon, Amsterdam, pp. 3–29 (2000).
Lipson, S. F. & Katz, J. L. The relationship between elastic properties and microstructure of bovine cortical bone. J. Biomech. 17, 231–240 (1984).
Rho, J.-Y., Kuhn-Spearing, L. & Zioupos, P. Mechanical properties and the hierarchical structure of bone. Med. Eng. Phys. 20, 92–102 (1998).
Meyers, M. A., Chen, P. Y., Lin, A. Y. M. & Seki, Y. 2008. Biological materials: structure and mechanical properties. Prog. Mater. Sci. 53, 1–206 (2008).
Zioupos, P. & Currey, J. D. Changes in stiffness, strength and toughness of human cortical bone with age. Bone 22, 57–66 (1998).
Ager, J. W., Balooch, G. & Ritchie, R. O. Fracture, aging and disease in bone. J. Mater. Res. 21, 1878–1892 (2006).
Carnelli, D., Lucchini, R., Ponzoni, M., Contro, R. & Vena, P. Nanoindentation testing and finite element simulations of cortical bone allowing for anisotropic elastic and inelastic mechanical response. J. Biomech. 44, 1852–1858 (2011).
Besdo, S. & Vashishth, D. Extended Finite Element models of introcortical porosity and heterogeneity in cortical bone. Comput. Mater. Sci. 64, 301–305 (2012).
Hing, K. A. Bioceramic bone graft substitutes: influence of porosity and chemistry. Int. J. Appl. Ceram. Tech. 2, 184–199 (2005).
Pearce, A. I., Richards, R. G., Milz, S., Schneider, E. & Pearce, S. G. Animal models for implant biomaterial research in bone: a review. Eur. Cell. Mater. 13, 1–10 (2007).
Lieberman, D. E., Polk, J. D. & Demes, B. Predicting long bone loading from cross-sectional geometry. Am. J. Phys. Anthropol. 123, 156–171 (2004).
Hillier, M. L. & Bell, L. S. Differentiating human bone from animal bone: a review of histological methods. J. Forensic Sci. 52, 249–263 (2007).
Mulhern, D. M. & Ubelaker, D. H. Differences in osteon banding between human and nonhuman bone. J. Forensic Sci. 46, 220–222 (2001).
Taylor, M. E., Tanner, K. E., Freeman, M. A. R. & Yettram, A. L. Stress and strain distribution within the intact femur: compression or bending? Med. Eng. Phys. 18, 122–131 (1996).
Heller, M. O. et al. Musculo-skeletal loading conditions at the hip during walking and stair climbing. J. Biomech. 34, 883–893 (2001).
Duda, G. N., Schneider, E. & Chao, E. Y. S. Internal forces and moments in the femur during walking. J. Biomech. 30, 933–941 (1997).
Zheng, N., Fleisig, G. S., Escamilla, R. F. & Barrentine, S. W. An analytical model of the knee for estimation of internal forces during exercise. J. Biomech. 31, 963–967 (1998).
Huiskes, R., Janssen, J. D. & Slooff, T. J. A detailed comparison of experimental and theoretical stress-analyses of a human femur. Mechanical properties of Bone 45, 211–234 (1981).
Bergmann, G., Siraky, J., Rohlmann, A. & Koelbel, R. A comparison of hip joint forces in sheep, dog and man. J. Biomech. 17, 907–921 (1984).
Bergmann, G., Graichen, F. & Rohlmann, A. Hip joint forces in sheep. J. Biomech. 32, 769–777 (1999).
Taylor, W. R. et al. Tibio-femoral joint contact forces in sheep. J. Biomech. 39, 791–798 (2006).
Duda, G. N. et al. Analysis of inter-fragmentary movement as a function of musculoskeletal loading conditions in sheep. J. Biomech. 31, 201–210 (1997).
Shahar, R. & Banks-Sills, L. Biomechanical analysis of the canine hind limb: calculation of forces during the three legged stance. J. Vet. Med. 163, 240–250 (2002).
Shahar, R., Banks-Sills, L. & Eliasy, R. Stress and strain distribution in the intact canine femur: finite element analysis. Med. Eng. Phys. 25, 387–395 (2003).
Currey, J. D. Bones: Structure and Mechanics (Princeton University Press, Princeton, 2002).
Lanyon, L. E., Magee, P. T. & Baggott, D. G. The relationship of functional stress and strain to the processes of bone remodeling: an experimental study on sheep radius. J. Biomech. 12, 593–600 (1979).
Van Buskirk, W. C. & Ashman, R. B. The elastic moduli of bone. Mechanical properties of bone. (Edited by Cowin, S. C.)AMD American Society of Mechanical Engineers. New York. 45, 131–143 (1981).
Katz, L. J. et al. The effects of remodeling on elastic properties of bone. Calcif. Tissue. Int. 36, S31–S36 (1984).
Norman, T. L., Vashishth, D. & Burr, D. B. Fracture toughness of human bone under tension. J. Biomech. 28, 309–320 (1995).
Reilly, G. C. & Currey, J. D. The development of microcracking and failure in bone depends on the loading mode to which it is adapted. J. Exp. Biol. 202, 543–552 (1999).
Kim, J. H., Niinomi, M., Akahori, T., Takeda, J. & Toda, H. Effect of microsctructure on fatigue strength of bovine compact bones. JSME Int. J. A48, 472–480 (2005).
Kim, J. H., Niinomi, M., Akahori, T. & Toda., H. Fatigue properties of bovine compact bones that have different microstructures. Int. J. Fatigue 29, 1039–1050 (2007).
Carter, D. R., Hayes, W. C. & Schurman, D. J. Fatigue life of compact bone-II. Effects of microstructure and density. J. Biomech. 9, 211–218 (1976).
Riggs, C. M., Lanyon, L. E. & Boyde, A. Functional associations between collagen fibre orientation and locomotor strain direction in cortical bone of the equine radius. Anat. Embryol. 187, 231–238 (1993).
Mason, M. W., Skedros, J. G. & Bloebaum, R. D. Evidence of strain-mode-related cortical adaptation in the diaphysis of the horse radius. Bone 17, 229–237 (1995).
Fratzl, P., Schreiber, S. & Boyde, A. Characterization of bone mineral crystals in horse radius by small-angle X-ray scattering. Calcif. Tissue Int. 58, 341–346 (1996).
Currey, J. D. The many adaptations of bone. J. Biomech. 36, 1487–1495 (2003).
Lee, T. C., Staines, A. & Taylor, D. Bone adaptation to load: microdamage as a stimulus for bone remodelling. J. Anat. 201, 437–466 (2002).
Porod, G. Chapter 2 in Small-Angle X-ray Scattering (eds. Glatter, O. & Kratsky, O.) (Academic, New York, 1982).
Sorensen, C. Light scattering by fractal aggregates: a review. Aerosol Science Tech. 35, 648–687 (2001).
Shinde, M., Das, D. & Rajesh, R. Violation of the Porod law in a freely cooling granular gas in one dimension. Phys. Rev. Lett. 99, 234505-1–4 (2007).
Dey, S., Das, D. & Rajesh, R. Spatial structures and giant number fluctuations in models of active matter. Phys. Rev. Lett. 108, 238001-1–4 (2012).
Joshi, M. B. et al. Phylogeography and origin of Indian domestic goats. Mol. Biol. Evol. 21, 454–462 (2004).
Acknowledgements
We thank D. Taylor, Trinity College, for his feedback on an earlier version of this paper. We thank Sampath Kumar, S. Sarma and M. Dixit for very helpful discussion and M. Dixit for help in storage of bone. We also thank the Material Science department at IITM for access to their experimental facilities.
Author information
Authors and Affiliations
Contributions
A.M., A.B. and R.R. contributed equally to the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary material for
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Mayya, A., Banerjee, A. & Rajesh, R. Mammalian cortical bone in tension is non-Haversian. Sci Rep 3, 2533 (2013). https://doi.org/10.1038/srep02533
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep02533
This article is cited by
-
Multiscale Effects of Collagen Damage in Cortical Bone and Dentin
JOM (2023)
-
A study of intracortical porosity’s area fractions and aspect ratios using computer vision and pulse-coupled neural networks
Medical & Biological Engineering & Computing (2019)
-
Identifying the animal species used to manufacture bone arrowheads in South Africa
Archaeological and Anthropological Sciences (2019)
-
Differences in femoral morphology between sheep (Ovis aries) and goat (Capra hircus): macroscopic and microscopic observations
Zoomorphology (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.