Introduction

Quantum key distribution (QKD)1,2 is one of the most realistic applications in quantum information. It aims at extending a secret key between two distant parties, commonly noted as Alice and Bob. The unconditional security has been proven even when an eavesdropper, Eve, has unlimited computation power permitted by quantum mechanics3,4,5,6.

The best known protocol of QKD is the BB84 protocol1 presented by Bennett and Brassard in 1984. In BB84, Alice encodes the key information randomly into the X and Z bases and sends quantum pulses to Bob. Bob measures the received pulses in two bases randomly. After that, they compare the basis through an authenticated classical channel. The key can only be extracted from the pulses where they use the same basis and this results in that on average half of the raw data is discarded. That is, the basis-sift factor is 1/2 in the original BB84 protocol. This factor can be improved by the efficient BB84 scheme proposed by Lo et al.7. In the efficient scheme, Alice and Bob put a bias in the probabilities of choosing the Z basis and X basis, which can make the basis sift-factor close to 100% in the infinitely long key limit. The efficient BB84 scheme is experimentally demonstrated in 20098.

In practical QKD systems, a highly attenuated laser or a weak coherent state source is widely used to substitute for a perfect single-photon source which is beyond state-of-the-art technology. A weak coherent state source contains multi-photon components (details shown in Methods). When multi-photon states are used for QKD, Eve can launch attacks, like the photon-number-splitting (PNS) attack9,10, to break the security. Since Eve could have a full control of the quantum channel, she can make the transmittance of multi-photon states to be 100% in the PNS attack. In a conventional security analysis11, Alice and Bob have to assume all the losses and errors come from the single-photon components in the worst scenario case. As a result, the performance of QKD is very poor. To improve the performance of the weak coherent state QKD, Hwang proposed the decoy-state method12. Instead of sending one coherent state, Alice sends pulses with different intensities, so that she can obtain more information to monitor the quantum channel. To maintain the detection statistics of coherent states with different intensities, Eve is not able to change the transmittances of single-photon and multi-photon state freely without being noticed by Alice and Bob. The security of the decoy-state method is proven13, along with various practical schemes14,15. Follow-up experimental demonstrations show that the decoy-state method is a very effective way to improve QKD performance16,17,18,19,20.

Naturally, we can improve the decoy-state method by applying the biased-basis idea of the efficient BB84 protocol. There are a few observations. First, Alice does not need to choose basis when she chooses the vacuum decoy state. Second, if Alice and Bob mainly choose one basis, say Z basis, for key generation, they effectively treat X basis as for quantum channel testing. In this sense, the functionality of X basis is similar to the decoy states. Intuitively, one may expect to combine decoy states and X basis together.

Here, we propose a new decoy-state method with biased basis choice, following the widely used decoy-state scheme, vacuum + weak decoy-state method15 (a quick review is shown in Methods), where Alice sends out pulses with three different intensities, vacuum (with an intensity of 0), weak decoy (with an intensity of ν) and signal (with an intensity of μ) states.

  1. 1

    Alice prepares all the signal pulses (μ) in the Z basis, where the final secure key is extracted from.

  2. 2

    She prepares weak decoy pulses (ν) in the X and Z with certain probabilities.

  3. 3

    If she chooses the vacuum decoy state, she does not need to set any basis.

  4. 4

    Bob measures the received pulses in the X basis and Z basis with probabilities px and pz, respectively.

The scheme is summarized in Table 1. In the new scheme, only 4 sets of preparations are used by Alice. Compared to the original vacuum + weak decoy-state method, where 6 sets are used, the proposed scheme can simplify the system and reduce the cost of random numbers. Later in the simulation, we will show that this scheme can also improve the QKD performance.

Table 1 List of Alice and Bob's operations. Alice prepares and sends Ntotal pulses, with . Bob measures the received pulses with certain probabilities, pz + px = 1
Full size table

Following the GLLP security analysis11, the key generation rate13,21 is given by

where q is the raw data sift factor, including basis-sift factor and signal-state ratio; Iec is the cost of error correction and the rest terms in the bracket is the rate of privacy amplification; f is the error correction inefficiency; Qμ and Eμ are the overall gain and quantum bit error rate (QBER); is the gain of the single-photon components and is its corresponding phase error rate; Q0 is the background gain; H(x) = −x log2(x) − (1 − x) log2(1 − x) is the binary Shannon entropy function. Note that in our scheme, the final key is extracted from Z-basis measurement results, so all the variables in equation (1) should be measured in the Z basis. The phase error rate cannot be measured directly, which, instead, can be inferred from the error rate in the X basis22.

The gain and QBER, Qμ and Eμ, can be measured from the experiment directly. Alice and Bob need to estimate and for privacy amplification. According to the model reviewed in Methods, we have and Q0 = Y0e−μ, where and Y0 are the yield of single-photon components measured in the Z basis and background rate, respectively. In order to lower bound the key rate equation (1), one can lower bound , Y0 and upper bound .

Since that both the vacuum state and the single-photon state are basis independent, the yields of vacuum states and single-photon states in different bases are equal

While a multi-photon state is basis dependent, whose basis information may be revealed to Eve by, for example, PNS attack9, so for any i-photon state (i ≥ 2), in general,

That is, depending on the basis information, Eve may set the yield of i-photon state different for the X and Z bases. As for the error rates, the phase error probability in the Z basis equals to the bit error probability in the X basis

Then, in the finite-key-size situation where statistical fluctuations should be taken into account22,23, we have

Given , we can upper bound by the random sampling argument (details shown in Methods). We need to point out that even though the single-photon state is basis independent, the error rates in two basis may not be the same

This can be easily seen by considering a simple intercept-and-resend attack where Eve measures all the pulses in the Z basis and then she will not introduce any additional error in the Z basis , but .

Results

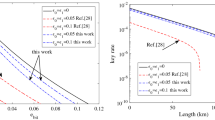
In our simulation, the parameters of the experimental setup are listed in Table 2. Statistical fluctuations are taken into account in the simulation (details shown in Methods). We compare the key generation rate in our scheme with that in the standard BB84 protocol with the vacuum + weak decoy-state scheme. The result is shown in Fig. 1.

Table 2 List of experimental parameters for simulation
Full size table
Figure 1
figure 1

Plot of key rate versus total transmittance.

The solid line shows the result of our scheme and the red line shows the result of the standard BB84 with the vacuum + weak decoy-state method. The simulation parameters are shown in Table 2. The confidence interval for statistical fluctuation is 5 standard deviations (i.e., 1–5.73 × 10−7). The expected photon number of signal state μ is 0.479. For each transmission loss, we optimize all the parameters, ν, Nμ, , , N0, pz and px.

Full size image

As one can see from Fig. 1, the key rate of the proposed biased scheme is larger than that of the standard BB84 with vacuum + weak decoy states by at least 45%. When the transmission loss is 0, the key rate improvement can go up to 80%. As the transmission loss increases, the improvement of the biased scheme decreases. This is because at a larger transmission loss, more pulses for decoy states are needed and Bob also needs a larger px to estimate the privacy amplification part in Eq. (1). The improvement comes from the fact that px is less than 1/2. As px approaches to 1/2, the biased scheme becomes similar to the original scheme, where px = pz = 1/2. It is an interesting prospective question how to apply our scheme to QKD systems with high channel losses24.

For a practical QKD system, one needs to optimize the bias px for the key rate. The dependence of the optimal bias on the transmission loss is shown in Fig. 2, from which we can see that the optimal pz is about 0.95 when the transmission loss is below 3 dB and decreases as the transmission loss increases. The minimal optimal pz is about 0.6, which is close to 1/2. That is why our scheme approaches the standard BB84 with the vacuum + weak decoy-state scheme as the transmission loss increases.

Figure 2
figure 2

Plot of optimal pz versus transmission loss.

Full size image

Discussion

In conclusion, we combine the decoy-state QKD with a biased basis choice to enhance the system performance. The key point of our scheme is increasing the raw data sift factor by setting all signal states in one (Z) basis. We take statistical fluctuations into account and use a rigorous method to upper bound the phase error rate of the single-photon components of the signal state. Comparing the result with that in the standard decoy-state BB84 protocol, we find an improvement in the key generation rate. Meanwhile, we reduce the complexity of the QKD system by assigning all signal states in the Z basis.

Methods

Model

The weak coherent state source is equivalent to a photon-number channel model and its photon number follows a Poisson distribution15:

Define Yi as the yield of an i-photon state; η as the transmittance of the channel measured in dB; Y0 as the background count rate. Then, in a normal channel when there is no Eve's intervention, Yi is given by:

The gain of i-photon states Qi is given by:

The overall gain which means the probability for Bob to obtain a detection event in one pulse with intensity μ is:

The error rate of i-photon states ei is given by

where ed is the probability that a photon hits the erroneous detector and e0 = 1/2. The overall QBER is given by

Without Eve changing Yi and ei, the gain and QBER are given by

Upper bound of

Here, we review the random sampling argument23: using the bit error rate measured in the X basis, , to estimate the phase error rate in the Z basis, , for privacy amplification.

If the key size is infinite, we know that . Otherwise, given , nx (the number of decoy states that Alice sends and Bob measures in the X basis) and nz (the number of signal states that Alice sends and Bob measures in the Z basis), we can give a probabilistic upper bound of such that it is lower than with a small probability Pθx

where θx is the deviation of the phase error rate from the tested value. Here, Pθx is a controllable variable and is equal to 10−7 in the simulation. We have

where the function ξx(θx) is given by

and qx = nx/(nx + nz). Given Pθx, we compute the value of ξx and find the value θx which is the root of equation (16). We get the probabilistic upper bound

Vacuum + weak decoy state

In this protocol, Alice and Bob use two decoy states to estimate the low bound of Y1 and the upper bound of e1. First, they implement a vacuum decoy state to estimate the background counts in signal states

Secondly, they perform a weak decoy state where Alice uses a weaker intensity ν (ν < μ) for the decoy state to estimate Y1 and e1. We have:

and

Note that in our scheme all the parameters for estimating are measured in the Z basis and the parameters for estimating are measured in the X basis. And we must lower bound Y0 to obtain the lower bound of the key rate15. The we get here will substitute ebx in equation (14).

Statistical fluctuation

Here, we consider statistical fluctuations for the decoy-sate method15. We need to modify the estimation of Y1, equation (19) and e1, equation (20).

The total number of pulses sent by Alice is composed of four cases

Since that Alice sends all signal states in the Z basis and the final key is only extracted from the data measured in the Z basis, the parameter q in equation (1) is given by

We follow the statistical fluctuation analysis proposed by Ma et al.25.

where , and are measurement outcomes which means that they are rates instead of probabilities. If we follow the standard error analysis assumption, uα is the number of standard deviations one chooses for the statistical fluctuation analysis. Note that and are used to estimate , so they should be measured in the Z basis. Here we use equation (14) to estimate the upper bound of with