Introduction

Single-cell studies of signaling pathways have provided compelling evidence that molecular noise can shape cellular signal-response systems1,2,3,4,5,6,7. However, the origin of signaling noise and how such noise shapes cellular information processing mechanisms at the molecular level remain unclear. Ladbury and Arold recently argued that “promiscuity” in protein-protein interactions (PPIs) is one of the main sources of noise in signaling networks8. This hypothesis stems from the observation that kinase-phosphatase interaction networks are characterized by a high degree of connectivity, a cacophony of cross-talk and extensive nonspecific interactions, rather than by formation of linear cascades of signaling events as once thought8,9,10,11,12. In budding yeast, for example, a recent study revealed that the Cdc14 phosphatase interacts with 53 different partners, including 23 kinases and 5 phostaphases13. Further, recent estimates of the protein interactome suggest that the number of binary PPIs is around 20,000 in yeast14 and 650,000 in humans15. Most of these PPIs have not been characterized and they appear to make little functional sense10,11. These suggest that the promiscuity of protein interactions is a wide-spread phenomenon that can give rise to complex stochastic effects that may shape cell signaling. Although this hypothesis identifies a main source for signaling noise, it does not identify the conditions under which such signaling noise influences system-level cellular information processing. A better understanding of stochastic effects could lead to new insights into how noisy interactions are integrated and maintained in cellular signaling networks. It could also provide some guidance in the targeted design and engineering of synthetic PPI circuits for specific functions by attenuating or exploiting signaling noise.

To address the extent to which PPIs in signaling networks result in substantial stochastic effects, we examined if and how kinase-phosphatase interaction networks can give rise to specific stochastic effects—called deviant effects—where the underlying fluctuations drive the behavior of the system substantially away from the prediction of the deterministic differential equations based on classical chemical kinetics16. In particular, we focused here on deviant effects in which the expected steady-state behavior of biological systems is substantially deviated in the presence of molecular noise. Compared with the effects from stochastic variability, which is often quantified simply by a statistical dispersion measure, such as the coefficient of variation17,18,19, such deviant effects may affect the regulation of an overall biological system in a more complex and less intuitive manner16,20. For example, such stochastic effects are incorporated in developmental mechanisms of various organisms—from primitive prokaryotes to higher eukaryotes—to stochastically diversify cell types21,22. Also, these effects are predicted to enhance sensitivity amplification of intracellular signal-response systems23. In signaling networks, deviant effects can play a particularly important role in shaping the intracellular information processing mechanism since the behaviors of downstream processes and correct cellular responses depend on the fidelity of signal levels to encode environmental information. While Samoilov and Arkin classified deviant effects16, the conditions under which they emerge in biological systems remain poorly understood. Since the noise level depends strongly on the architecture of biological networks24,25,26,27,28, noisy interactions of proteins may also give rise to deviant effects in cellular information processing. However, the vast extent of PPI networks makes it difficult to discern if a given signaling network can exhibit deviant effects and which interactions are responsible for the stochastic effects.

Rather than focusing on the structural properties of a specific signaling system that exhibits deviant effects, we focused here on topological features capable of giving rise to deviant effects purely from interactions of enzymatic cycles in a bottom-up fashion. To this end, we developed a computational framework to search for deviant effects and systematically explored a range of enzymatic circuit graphs. We determined that the node of each of these circuit graphs is a simple enzymatic cycle that in isolation does not result in deviant effects (Fig. 1a). We analyzed the network conditions under which high levels of deviation can arise in a wide range of enzymatic circuit graphs with three, four and five nodes. We found that, whereas most of the networks we studied exhibit only minor levels of deviation, a small fraction of them is capable of exhibiting deviant effects and shares a common architectural feature. These networks can also give rise to substantial levels of stochastic variability under different conditions, indicating that they have rich stochastic dynamics repertoires. We found that deviant effects can emerge purely from interactions of signaling proteins and that an increase in network size can substantially increase the level of such stochastic effects. We showed that deviant effects can not only alter the steady-state response but also affect the shape and the sensitivity of the stimulus/response curve of signaling systems. These results may have important implications for our understanding of the evolution of cellular signaling systems as well as for the engineering of synthetic cellular signaling networks.

Figure 1
figure 1

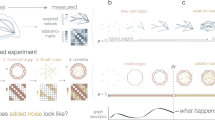
A bottom-up approach to analyze architectural features of deviant effects.

(a) The structure, the mean time evolution and the steady-state average of the network based on a single two-state protein. Here, X is the inactive form of the protein; X* is the active form of the protein; Ef is the enzyme to catalyze the activation of the protein; and Eb is the enzyme to catalyze the inactivation of the protein, while k1 and k2 are the basal activation and inactivation rate constants and kf and kb are the catalytic activation and inactivation rate constants. The superscript ss indicates the steady-state (stationary) random variable whereas the superscript ds indicates the deterministic steady state. (b) An illustration of how enzymatic circuit models are built from the signaling protein motif. Activation of node 1 by node 2 is shown on the left. The active form of the protein in node 2 is used as the enzyme to catalyze the activation of the protein in node 1. Inhibition of node 1 by node 2 is shown on the right. The active form of the protein in node 2 is used as the enzyme to catalyze inactivation of the protein in node 1. (c) An illustration of our framework to analyze the topological features that give rise to deviant effects from simulation of a range of enzymatic circuit models. Networks are generated using a set of constraints (see Materials and Methods) and each node has a set of parameter values. From these the steady-state average of the active form of node 1 is computed for the stochastic model and the corresponding deterministic model and the deviation level is measured.

Full size image

Results

Model setting

In this study, we defined deviant effects to be stochastic effects in which the molecular fluctuations alter the expected steady-state behavior of a signaling network substantially. To study if and how interactions of signaling proteins give rise to the deviant effects, we built signaling network models from the enzymatic circuit motif (Fig. 1a). This enzymatic circuit motif has been utilized to build larger network models to study dynamical properties in different contexts, such as studies of adaptation, switch-like responses, bistability and oscillations29,30,31,32. In this network module, we assume that each signaling protein has two functionally distinct states: the inactive state (X) and the active state (X*). Transitions of the states in a protein can take place at small basal rates; transitions of signaling proteins are mainly regulated by two enzymes: activation of proteins is catalyzed by Ef, while inactivation is catalyzed by Eb. These enzymes are the inputs of the module, while the active state of the protein is the output that in turn can influence other nodes by acting as a catalytic agent (Fig. 1b). In our models, the kinetics of enzymatic reactions simply follows that of bimolecular reactions (Fig. 1a). This allows us to relate possible deviation in the output of the module and the covariance between the inputs and the output. That is, only when the inputs and the output are sufficiently correlated, can the output have possible deviations, provided that the two inputs are deviation free. On the other hand, when Cov(X*, Ef) and Cov(X*, Eb) are both negligible, we will have insignificant levels of deviation in the output and when the two input enzymes are constant and have no deviations, the output have no deviations because both Cov(X*, Ef) and Cov(X*, Eb) become zero. This safeguards the steady state of the isolated module from deviant effects (Supplementary Information (SI) section S1).

To generate signaling networks from this motif, we imposed a set of rules that restricts how signaling proteins can be connected (see Materials and Methods). With this network generation constraint, each of the deterministic kinetic models is found to have only one positive steady state (see Materials and Methods). To search for deviant effects, we simulated each of the networks with various parameter combinations and we measured deviation levels by computing the relative difference between and , the steady-state averages of the active protein in node 1 in the stochastic model and the corresponding noise-free deterministic model, respectively (Fig. 1c and see Materials and Methods).

Positive relations between the deviation and noise levels

We first examined three-node networks. We generated 26 network structures, each of which was simulated with 64 distinct parameter combinations. Our analysis shows that our three-node networks do not result in deviant effects (Fig. S1). Since noise is a necessary factor in giving rise to deviant effects, we set out to understand if there is a positive relationship between deviation levels and noise levels. To uncover which networks have the potential to give rise to higher deviation levels, we measured the average of the five highest deviation levels for each three-node network. Similarly, we measured the potential to exhibit high variability by computing the average of the five highest noise levels for each network. We found that, while the three-node networks we studied exhibited only minor levels of deviation, a positive correlation does exist between the potential for the deviation and the potential for stochastic variation (Fig. S2). Our analysis of networks of different sizes was consistent with this result.

Deviant effects from inhibition of a double positive feedback loop

Next, to check if adding another node to the networks would give rise to deviant effects, we turned our focus to four-node networks. We generated 108 four-node networks, each of which was simulated using 256 distinct parameter combinations. This totaled 27,648 distinct network/parameter combinations. We then simulated the stochastic model and the deterministic model of each combination to calculate the deviation level. While this simulation revealed that most networks are not characterized by deviations, a small fraction of the combinations indeed exhibited extensive deviation (Fig. S3). To determine if the four-node networks also have a positive correlation between the potential for deviation and the potential for stochastic variation, we calculated the average of the ten highest deviation levels and the average of the ten highest noise levels to determine the deviation potential and the stochastic variation potential for each network, respectively. We found that, like in the three-node networks, higher deviation is strongly correlated with higher noise levels (Fig. 2a). In addition, we found that, among all four-node networks we studied, two networks surpassed the deviation and noise potentials (Fig. 2a). Interestingly, the two outlier networks (N4A and N4B) exhibited isomorphism; they both had the same topology with respect to node 1 in that it had a double positive feedback loop between node 1 and its neighboring node while these two nodes were inhibited by the other two nodes (Fig. 2b).

Figure 2
figure 2

Deviation and noise levels of four-node networks.

(a) A scatter plot showing the potential for high deviation and noise levels. Here, each red open circle represents the average of the ten highest noise levels (x-axis) and the average of the ten highest deviation levels (y-axis) from each network. The red circles surrounded by the light blue oval represent the two topologies with the highest deviation and noise levels. (b) The network structures that give the highest deviation and noise potential (N4A top and N4B bottom). Note that N4A and N4B are isomorphic with respect to node 1. (c) Correlations between the noise level and the deviation level of N4A and N4B. Each data point represents the noise and deviation level of one of the two networks (blue circles for N4A and green squares for N4B) for a specific parameter combination. (d) A distribution of that gives the highest level of deviation from N4A. (e) A distribution of that gives one of the highest levels of variability and a low level of deviation from N4A. (f)–(i) The distributions of the parameter combinations, each of which results in the deviation level or the noise level reaching a specified threshold value. The two numbers in the parentheses in each panel indicate the threshold value (left) and the fraction of the total samples that reach this value (right).

Full size image

Are N4A and N4B just random outliers? In the 4-node network models that we studied, 17 out of the 27,648 network/parameter combinations exhibited deviation levels greater than or equal to 0.5. These 17 combinations are made up of only two network structures; 8 are based on N4A, while 9 are based on N4B (Table S1). The composition of the combinations with higher deviation shows a clear correlation between these networks and higher deviation levels. At the same time, most of the parameter combinations in these networks did not result in high deviation levels. Indeed, while there was only a small fraction of combinations that exhibited significant levels of deviation in our 4-node network experiment, this may be simply explained by the relatively small parameter space that we covered in the experiment, which only included a small portion of the high deviation region. These indicate that having specific network structures such as N4A and N4B is a necessary condition for deviant effects, but not a sufficient condition and parameter combinations on top of network structure constraints play an important role in exhibiting deviant effects.

Several biological systems, such as the segmentation clock in zebrafish and secretion of Gonadotropin-releasing hormone, were reported to include similar architectural features (i.e., multiple inhibition connections to a double positive feedback loop) and exhibit synchronized oscillations given much higher nonlinearities and sufficient time-delays in their reaction kinetics33. Also, inhibition of a double positive feedback loop can be seen in G1 and S phases of the yeast cell cycle system in which Wee1 and Myt1 kinases inhibit Cdk1 which is activated by a double positive feedback loop with Cdc2534,35.

To understand if our results were specific to the reaction kinetics we considered for the two-state protein motif or if they were applicable more generally, we changed the reaction kinetics of each node to Michaelis-Menten kinetics and analyzed the deviation and noise levels in the same set of four-node networks. While the added nonlinearity and complexity amplified the deviation and noise levels in general, our results remained intact because the potential for the deviation had a positive relation with the potential for stochastic variation. The same networks, N4A and N4B, also had a substantially higher deviation potential as well as noise level potential compared with the other networks (SI section S2 and Fig. S4).

The topology of N4A and N4B includes a double positive feedback loop and two nodes that inhibit the feedback loop. From a functional perspective, having two inhibition nodes may not seem to change the dynamics of node 1 by much compared with having only one strong inhibition node. In N4A, for example, regardless of the effect of node 4, the steady-state behavior may not change, provided that node 3 provides a strong inhibition within a noise-free, deterministic framework. We note that these dynamics similarities can also be seen in the corresponding network with enzymatic reaction kinetics in which the system can exhibit bistability regardless of the effect of node 4 (Fig. S5). However, our results provide strong evidence that inclusion of such interactions with seemingly neutral effects can substantially increase the level of deviation.

Deviation associated with higher correlation between the feedback nodes

Next, we examined how the topology of N4A and N4B can give rise to deviant effects. Our four-node network simulation data suggest that higher levels of deviation are based on lower steady-state in the stochastic models (Fig. 2d and Fig. S3). With the structure of N4A, , the covariance of the active forms of nodes 1 and 2 in the steady state, is expected to be positive because the positive feedback loop positively correlates node 1 and node 2, while is expected to be negative because inhibition of node 1 by node 3 causes these two nodes to be negatively correlated. Thus, in order to decrease the steady state in the presence of molecular noise in this setting, must be higher or must be lower. That none of the three-node networks exhibited high levels of deviation suggests that, upon addition of node 4, the covariances change substantially to reflect a decrease in the stochastic steady-state average of N4A. To analyze this, we measured how the values of and changed based on the inhibition of node 2 by node 4 in N4A. We found that, by adding node 4, the range of increased by a factor of ten, while the range of only changed by a factor of two (Fig. S6). This suggests that lowering the stochastic steady-state average with inhibition of node 2 by node 4 is associated with an increase in correlation between node 1 and node 2.

Parameter conditions for high deviation and noise levels

While it is clear that the topology of N4A and N4B can substantially strengthen the effects of underlying molecular noise to generate higher deviation and noise levels, how this occurs remains unclear. To gain better insights into the conditions under which this topology generates the highest levels of deviation and noise, we first analyzed the distribution of the deviation and noise levels in the 256 parameter combinations of N4A and N4B. Interestingly, we found that the condition for higher deviation levels is not necessarily the same as that for higher noise levels. Indeed, some parameter sets resulting in higher noise levels exhibit very small deviation levels, whereas higher deviation levels appear to be coordinated with higher noise levels (Fig. 2c).

To gain further insights into the stochastic dynamic repertoire of the topology of N4A and N4B, we analyzed the steady-state distributions of N4A in two sets of parameter combinations resulting in (i) high deviation and noise levels and (ii) a low deviation level and a high noise level. The steady-state distribution of the former shows a long tail with a short head (Fig. 2d). This suggests that the active form of node 1 has a low value most of the time, while it occasionally jumps to higher molecular counts for very short periods of time. The stochastic steady-state average is close to the peak of the distribution and is much lower than the corresponding deterministic steady state (Fig. 2d), suggesting that molecular noise can make the inhibition of node 1 stronger and/or the activation of node 1 weaker. Similarly, the steady-state distribution for the latter has a long tail with a short head (Fig. 2e). However, the steady-state average is even lower, suggesting that the activity of the double positive feedback loop is weaker.

To clarify the conditions under which the topology of N4A and N4B gives rise to high deviation, we analyzed the distribution of parameter values resulting in deviant effects. In addition, to compare the conditions for the high deviation measure with those for the high noise level measure, we also analyzed the distributions of parameters with high noise levels. To this end, we simulated the stochastic model and the deterministic model of N4A with a finer parameter increment with each node having 25 different parameter combinations, resulting in 390,625 distinct parameter combinations in total (see Materials and Methods). We counted the number of parameter combinations that resulted in deviation and noise levels reaching various thresholds (Fig. S7). Using this information, we examined each parameter distribution for the deviation case and the noise case and compared them based on fractions of the combinations reaching given thresholds. The results from the deviation level of 2.0—a level that only 0.01% of the total parameter combinations can achieve—indicate a clear pattern of parameter conditions in which the double positive feedback loop between node 1 and node 2 can be potentially strong and the inhibition from the other two nodes is strong enough to keep the active forms of node 1 and node 2 at a low level (Fig. 2f), making the activity of the positive feedback loop weak most of the time. However, due to the underlying fluctuations, the inhibition from nodes 3 and 4 occasionally becomes weaker, which in turn allows the active form of nodes 1 and 2 to increase rapidly because of the strong positive feedback between them.

The results from a noise level of 1.45—a level that only 0.02% of the total parameter combinations can achieve—also indicate a clear pattern of parameter conditions (Fig. 2g). However, this parameter trend is very different from that of the high deviation level, suggesting that this network topology is able to give rise to high deviation levels as well as high noise levels if parameter values are changed. As we lower the deviation level of parameter distributions to 1.0, the pattern is distorted (Fig. 2h). Also, with a noise level of 1.2, the pattern of parameter conditions becomes distorted (Fig. 2i). Interestingly, however, the parameter distributions from lower deviation and noise levels are more similar. This is also evident in Fig. 2c where the parameter values giving rise to higher deviation levels also exhibit higher noise levels.

Amplification of deviation by adding functionally irrelevant interactions

Our results suggest that in certain architectures of enzymatic circuits, stochastic effects can substantially amplify with an increase in the size of protein interactions. To further test this hypothesis, we explored 436 five-node networks with 1,024 different parameter combinations, resulting in 446,464 network/parameter combinations. The steady-state results from the deterministic models and the stochastic models yielded an increase in the higher deviation levels compared with the four-node networks (Fig. S8). To identify which networks can give rise to high deviation levels as well as high noise levels, we computed the average of the ten highest deviation levels as well as the average of the ten highest noise levels for each network. The results indicated that four networks had a much higher deviation potential compared with the other five-node networks and they also had the highest noise level potential (Fig. S9a). Interestingly, these four networks are all extensions of N4A and N4B in which the fifth node was added to activate one of the inhibitory nodes (Fig. S9b). Furthermore, we found that the networks with the eight highest deviation potentials were classified into four distinct topologies with respect to node 1 and they were all extended from N4A and N4B. To observe how deviation levels changed based on different extensions from this N4A and N4B, we measured the distribution of deviation levels for each of these four topologies. We found that the distributions of the deviation levels from the two topologies with the highest deviation levels (in which the fifth node is an activator node of an inhibitor node) were in agreement and the networks of these topologies were capable of generating substantially higher deviation levels than N4A and N4B (Fig. 3a). On the other hand, when node 5 is added as an inhibitory node, deviation levels did not increase compared with N4A and N4B and they had the same type of distributions (Fig. 3a). This suggests that a stronger inhibition of the double positive feedback loop can result in higher deviation levels.

Figure 3
figure 3

The five-node networks with the highest levels of deviation.

(a) The distributions of the deviation levels from the top four network topologies compared with the distribution of the deviation levels from the four-node topology with the highest deviation potential. Each of the five-node topologies here represents two isomorphic networks with respect to node 1. (b) A specific five-node topology with the highest deviation levels used for sensitivity analysis. (c)–(g) Sensitivity analysis. Heatmap plots showing how the deviation level changes based on changes in parameters in a particular node while keeping the parameters of the other nodes fixed. The black circles indicate the base parameter values.

Full size image

To gain further insights into the conditions under which very high levels of deviation arise, we focused on one specific five-node network with high deviation levels (Fig. 3b) and performed additional simulations with finer parameter changes. We chose one parameter combination that had one of the highest levels of deviation and changed the parameter values one node at a time while keeping the parameter values in the other nodes fixed. The results from this sensitivity analysis showed that the ability to maintain a very high level of deviation and to change the deviation level with respect to parameter changes varies depending on the node. While the deviation level can dramatically decrease based on changes in parameter values from nodes 1 and 2 (Fig. 3c and d), it changes more gradually based on changes in the parameter values of node 3 (Fig. 3e). Interestingly, the results from nodes 4 and 5 indicate that the high level of deviation is robust to changes in these nodes and a much higher level of deviation compared with the three-node and four-node networks can be maintained regardless of the values of the parameters (Fig. 3f and g). This suggests that, while the addition of nodes 4 and 5, at first glance, does not seem to make a lot of influence in the system dynamics, particularly when the inhibition of node 1 by node 3 is already strong, it has a substantial impact in terms of the amplification of deviation levels. Also, these differences in deviation-level sensitivity suggest that molecular noise can shape steady-state stimulus/response curve of signaling systems. Indeed, our simulation results based on applying inhibitory stimuli to various nodes of the network shown in Fig. 3b showed that molecular noise can make the steady-state response more sensitive to one type of stimulus while it can also make the steady-state response more robust to another type of stimulus (Fig. S10). This suggests that molecular noise can give signaling systems a means of being more sensitive to proper signals and more robust to cross-talk signals. Taken together, our results indicate that deviant effects can emerge from an increase in the size of the enzymatic circuit with the addition of seemingly uninfluential protein interactions (Fig. 4) and evolutionary trajectories to amplify deviation levels could have positive effects on mechanisms of cellular signaling.

Figure 4
figure 4

Pathways to increase the deviation level from three-node to five-node topologies.

This shows potential trajectories that increase the deviation level with an increase in the network size. The solid arrows that connect the topologies indicate a substantial amplification in the deviation level, while the dashed arrows indicate neutral transitions with no (substantial) changes in the deviation level.

Full size image

To test the generality of the emergence of deviant effects associated with an increase in the size of enzymatic circuits, we changed the parameter settings in several ways and simulated the chemical kinetic models of the same set of three-node and four-node enzymatic circuit networks. Our analysis showed that four-node networks have higher deviation and stochastic variation levels than corresponding three-node networks and, interestingly, that the same four-node network topology exhibits substantial deviation and noise levels (Fig. S11). These results provide strong evidence that the two types of stochastic effects do indeed have a general tendency to amplify as the size of enzymatic circuits increases.

Discussion

Among the fundamental problems in molecular systems biology is the elucidation of the relation between molecular interaction networks and their dynamical behaviors. While the large complexity of biological systems makes this problem challenging, an exploratory approach to link the architectural features of the system to specific dynamical properties helps us understand general design principles that may be applicable to many organisms. Here, by taking a bottom-up approach, we explored a large number of signaling network conditions to search for unifying properties that can result in deviant effects. We found that, while most of the networks exhibit no deviant effects, a small fraction of the networks does give rise to deviant effects and these few networks have a common network feature. Interestingly, while these networks can also exhibit very high levels of stochastic variability, the conditions leading to these two types of stochastic effects are different. By examining the topological features of these networks via incremental changes in the network size, we found that deviant effects emerge from the integration of certain protein interactions that do not qualitatively influence the dynamics of the base network given the noise-free assumption. In addition, we showed that these stochastic effects can influence not just the variability and the average level of intracellular signals but also the sensitivity of the stimulus/response curve in signaling pathways, extending the list of biological mechanisms that make the stimulus/response curve more sensitive23,29,36. A previous study showed interesting stochastic effects called stochastic focusing where sensitivity of signal-response systems can be amplified with nonlinear, hyperbolic inhibition reactions, whose mean rates become different from the corresponding fluctuation free, deterministic reaction rates23. Our results showed that deviant effects can make signaling networks more sensitive to certain stimuli and to be more robust to others. Such sensitivity differentiation features may be particularly important for signaling pathways that are characterized by a high degree of cross-talk to respond to the “right” signal correctly and to ignore the other signals.

Our findings have two important implications. First, they suggest that various architectures of signaling networks with similar dynamical behaviors can have substantially different stochastic effects. This may improve the development of synthetic signaling circuits by taking the effects of molecular noise into account in the design and implementation of the circuits. This is consistent with a previous synthetic biology study that showed that a native gene circuit and a synthetic one designed to regulate the competence state of Bacillus subtilis have widely different stochastic effects even when their deterministic models predict the same behavior between the two28.

Second, our findings suggest a partial explanation for how large signaling networks with many nonfunctional elements evolved and how they are maintained in cells. Our results suggest several potential evolutionary trajectories that can substantially increase the deviation level while the dynamics of the system remains intact. Thus, if biological circuits with deviant effects have selective advantages, then an increase in the circuit size can occasionally lead to the emergence of such stochastic effects, resulting in an increase in fitness. A previous explanation for why there are so many PPIs in signaling networks suggests that a large number of PPIs may be noisy and would result from (nearly) neutral mutations37. Like our explanation, this one does not couple an increase in the complexity with an increase in fitness. However, if biological networks are assumed to have the intrinsic tendency to grow larger38, then neutral mutations can increase the complexity of PPIs. Our explanation does not contradict this explanation; rather, it complements it by suggesting that the integration of some noisy interactions can lead to higher fitness.

Signaling networks are undeniably complex with many unknowns and nonfunctional interactions. To analyze the properties of such systems, some level of simplification is necessary. In this study, we utilized simple models of interactions of small numbers of signaling proteins to attempt to gain insights into the architectures of signaling networks that can produce deviant effects. To this end, we have made several assumptions to make our computational study feasible and to reduce the complexity of the models. While such a simplification may not be able to capture the dynamical properties of the system quantitatively, it allowed us to explore a large number of enzymatic circuit models to search for the network conditions necessary for deviant effects. Similar approaches to exploring molecular network topologies to search for a given function have also led to better design principles for various response dynamics32,38, oscillations31,39 and reliable information processing mechanisms25,27, as well as understanding of the evolutionary process in network structures for a given function39,40,41. There are limitations in our approach. For example, due to high computational requirements, we were only able to explore limited network/parameter search space for analysis of stochastic effects. Because of this, we cannot say whether or not our findings are generally applicable to all signaling network structures capable of exhibiting deviant effects. However, we believe that our bottom-up approach is a powerful tool to explore not just architectural conditions for various dynamical effects of molecular noise but also potential incremental evolutionary trajectories to increase such effects.

Methods

Network generation constraints

The constraints that we imposed for network generation were as follows: (i) each node was allowed to influence at most one other node; (ii) each node was allowed at most one activation and one inhibition; (iii) if a network had a feedback loop, it involved node 1; and (iv) all nodes in the network were connected.

Fixed point analysis of deterministic models

To count the number of positive steady states in each of the deterministic models in our settings, we utilized the chemical reaction network (CRNT) toolbox (http://www.crnt.osu.edu/CRNTWin). The fixed-point analysis by the CRNT toolbox is based solely on the structure of the model and independent of the values of the model parameters. We applied the CRNT toolbox to all possible reaction network models and we found that each of the deterministic reaction network models with the original reaction kinetic scheme has only one positive steady state.

The mean time evolution

Let be a discrete-state Markov process, which represents the molecular count of the active form of node i at time t. Then, from the basic results of stochastic chemical kinetics42, the mean time evolution of in our setting is characterized by:

where Xi(t), and are the inactive form, the enzyme to catalyze the activation and the enzyme to catalyze the inactivation of node i at time t, respectively, while k1 and k2 are the basal activation and inactivation rate constants and kf and kb are the catalytic activation and inactivation rate constants. Here, if the the effects of the molecular fluctuations on the system dynamics can safely be ignored, then the average of products can be expressed by the product of averages since the covariance terms become zero (e.g., ). Thus, when assuming that there are no fluctuations in , we can express as a deterministic process and we can characterize the mean time evolution of by the ordinary differential equation based on corresponding mass-action kinetics as follows:

The definitions of the stochastic and deterministic steady-state average

We define to be a random variable characterizing , a stationary discrete-state Markov process, which represents the molecular count of the active form of node i with the time-invariant, steady-state distribution. Since the underlying Markov chain of each of our stochastic models is irreducible and positive recurrent, has a unique steady-state distribution. , the probability mass function of this random variable is, thus, characterized by , the probability that . Hence, , the stochastic steady-state average of , is defined by .

is the deterministic counterpart of the steady-state average and it denotes by making the fluctuation-free assumption. Here, is a stationary, continuous Markov process representing the average molecular count of the active form of node i (i.e., the stationary limit of Eq. 2).

Procedure for the main simulations

The deterministic steady-state average of the active form of node 1, , was computed by simulating the system of ordinary differential equations derived from the mass-action kinetic model of each network (i.e., a system of Eq. 2) and checking if the relative change in was less than 0.05 for every 1.0 time unit. The stochastic steady-state average of the active form of node 1, , was computed by simulating 5,000 runs of the stochastic chemical kinetic model of each network via Gillespie's stochastic simulation algorithm43 and periodically checking if the relative change in was less than 0.05 for every 1.0 time unit. In our model setting, the total molecular count of each protein is conserved and set to be 50. To capture small differences in the affinities of protein interactions8, we set the value of each catalytic reaction parameter to be 1 or 5. Since each node has two catalytic reaction parameters (i.e., kf and kb), an N-node network model has 4N parameter combinations with our setting. The basal rate constants, k1 and k2, are assumed to be much smaller. We set the values of these parameters to be 0.1. Note that these parameters are valuated in arbitrary time units. To test the correctness of our simulations, we chose a 3-node network models with specific parameter combinations which are known to be deviation free. The results from this control experiment shows the correctness of our simulation (Fig. S13).

Measure for deviation and noise level

As defined in Samoilov & Arkin (2006)44, the deviant effects are broadly discrete stochastic effects which drive the behavior of the system substantially away from the prediction of the deterministic differential equations based on classical chemical kinetics (or mass-action kinetics). Here, we studied the deviant effects in a specific context, that is, the contribution of molecular fluctuations to substantially deviating from . To this end, we defined the deviation level to be the relative distance of from and computed , where the small constant factor, , was used to discourage a very low level of (i.e., ) from achieving a high level of deviation when the absolute change is minimal.

The noise level of biological systems is often quantified using a measure of the dispersion such as the Fano factor and the coefficient of variation17,18,45. Here, based on the coefficient of variation, noise level was computed to be , where the small constant factor, , was used to discourage a very low level of (i.e., ) from achieving a high noise level when the absolute fluctuation effects are minimal. In this study, we set and to be 1.

Simulations for detailed analyses of the parameter conditions of N4A

For the analysis of the parameter conditions of N4A, we chose the values of the parameters in each node to be 1, 2, 3, 4, or 5. Since each parameter took 5 different values, we had 390,625 different parameter combinations. We only utilized the results from simulations that terminated before the predefined runtime limit. For the sensitivity analysis of the 5-node network, each parameter took values from 1.0 to 5.0 with increment of 0.1.