Introduction

Magnetic anisotropy is not only the origin of long-range-magnetic-order in low dimensional system1, but also plays a vital role in determining the magnetic properties for magnetically hard, magnetically soft2, high-frequency magnetic materials3, ultrahigh density magnetic recording media and spintronic materials. Recently, the growth and magnetic properties of single crystal Fe film on Si(111) surface have been investigated owing to its application in integration of magnetic devices in Si-based technology and new opportunities in spintronics4,5,6,7,8,9,10,11. The research of Fe ultrathin film magnetization has approached down to the atomic level by a powerful spin-polarized scanning tunneling microscopy (SP-STM)12,13,14. In the case of bcc Fe film grown on Si(111) substrate, the six-fold symmetry of magnetic anisotropy energy exists only when magnetization is confined strictly in the Fe(111) plane. A small structural modification is sufficient to destroy the six-fold symmetry as a result of the contributions from other magnetic anisotropy energies7,8. In our previous work, we observed that the six-fold symmetry of the in-plane resonance field for Fe(111) film was changed into the superposition of a four-fold and a two-fold contribution due to the presence of atomic step of the vicinal substrate15. Furthermore, we also observed some difference between ferromagnetic resonance (FMR) results and magnetization measurements. FMR results demonstrated that the azimuthal angular dependence of in-plane resonance field is a six-fold symmetry with a weak uniaxial contribution, while the remanence of hysteresis loops displays a two-fold one16. Therefore, the analysis of the magnetic anisotropy and magnetization reversal should be carried out carefully for Fe(111) films on Si(111) substrate.

Up to date, various methods, such as magnetic hysteresis loop measurement, torque measurement17, ferromagnetic resonance (FMR)7, rotational magneto-optic Kerr effect (ROT-MOKE)18 and magnetic transverse biased initial inverse susceptibility and torque (TBIIST)19, have been developed to determine the magnetic anisotropy constants. Since the coherent domain rotation magnetization reversal for ultrathin film is not always occurred, especially when the applied field is lower than saturation field, the detailed information regarding the magnetic anisotropy cannot be distinguished precisely from the magnetization hysteresis loops. Alternatively, magnetoransport method has been proved to be an ideal probe of magnetic anisotropy constants in the thin single layer films by anisotropic magnetoresistance (AMR)20,21,22,23,24,25,26, which determines the anisotropy field strength by realization of a coherent magnetization reversal (Stoner-Wohlfarth-like). This can be achieved by applying a sufficiently large field to guarantee a true single-domain rotation. Here, we carried out the AMR measurements in ultrathin single crystalline Fe film on vicinal Si(111) substrate. On the basis of AMR curves, the angle between the magnetization and magnetic field and hence the normalized magnetic torque can be derived. Finally, the uniaxial magnetic anisotropy, first- and second-order magnetocrystalline anisotropy constants were precisely obtained by fitting the normalized magnetic toque curves. Our work suggests that the extremely sensitive AMR can provide the detailed contributions of various magnetic anisotropy constants, including the first- and second-order magnetocrystalline anisotropy constants, as well as step-induced in-plane uniaxial magnetic anisotropy constant, of ultrathin Fe single crystal film on vicinal Si(111) surface.

Results

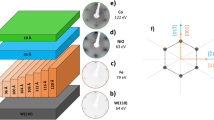
Figure 1(a) shows the schematic configuration of the sample and the coordinate system used in our AMR measurements and data analysis. Although the substrate supplier declares that the Si(111) substrate with orientation accuracy is 0.10° (nominal miscut angle β = 0.10°), a local miscut varies from point to point on the Si surface will take place due to cutting imperfection or mass transport under the direct heating. Recently, we adopted a novel method to tune the terrace width of Si(111) substrate by varying the direction of heating current27. Large scale images (850 nm × 850 nm) of the Si (111) substrate were employed to determine the local variation of miscut angles. The typical large scale STM images indicates that the narrower terraces are companied by a very broad (>400 nm) terrace Figure 1(b). From the section line profile along the perpendicular direction to the terrace steps (Inset of Fig. 1(b)), a single atomic step in Si(111) surface is about 0.30 nm high can be estimated, which is in good agreement with the value reported by Lin et al28. On the basis of the relation between atomic height h and terrace width w, β = arctan(h/w), the local miscut angle β can be various from 0.04° to 0.30° with a mean miscut angle of 0.10°. The sharp LEED pattern plotted in figure 1(b) demonstrates an atomically flat Si(111)-7 × 7 recostructured surface.

Figure 1
figure 1

The schematic configuration of the sample preparation and coordinate system used in AMR measurements and data analysis and STM images of sample surface.

(a) Schematic configuration of the sample and the coordinate system used in our AMR measurements and data analysis; (b) STM image and LEED patterns of 0.1° vicinal Si(111)-7 × 7 reconstructured surface; (c) STM image and LEED patterns of 2 × 2 iron silicide phases obtained at annealing temperature Ta = 700 K for 10 min after 1.5 ML Fe deposited on 0.1° vicinal Si(111) surface; (d) STM image and LEED patterns of 21 ML Fe on p(2 × 2)/Si(111).

Full size image

Figure 1(c) illustrates the STM image of the iron silicide template on the Si (111) substrate and the corresponding 2 × 2 LEED pattern. The iron silicide template comprises of steps separated by the flat p(2 × 2) reconstructed terraces. Compared with Si(111)- 7 × 7 recostructured surface, the step edges in the STM image for p(2 × 2) iron silicide reconstructed surface are not so sharp owing to the random diffusion of Fe atoms on Si substrate and the intermixing between Fe and Si atoms. The atomically flat terraces are generally used as a template for preparing ultrathin Fe single crystalline film. Fig. 1(d) shows the STM image of the iron deposited on p(2 × 2) iron silicide (111)/Si(111) surface for 21 ML and the LEED pattern. The LEED pattern indicates that three-fold symmetry still exists even for a thickness reaching 21 ML, suggesting a bcc Fe(111) film. The epitaxial relationships between the Fe(111) film, the iron silicide template and the Si substrate are following29: and iron silicide . Owing to the large lattice mismatch, STM topographic image shows that Fe atoms aggregate immediately into three-dimensional (3D) islands. The first stage is the growth of uniformly strained wetting layers and elastic energy increases fast with film thickness. The constrained film becomes unstable at a critical thickness and three dimensional islands appear for strain relief. With further increasing film thickness, misfit dislocations are introduced to further relieve stain resulting in deeper facets, dome and ridge-trough structures. The section line in the insert of figure 1(d) indicates that the surface corrugation of grainy thin Fe(111) is rather large. In our previous work, the effect of strain at the Fe/FeSi interface on the magnetic anisotropy has been discussed30. Since thickness of Fe film (about 21 ML) is far thicker than the critical thickness, the strain is released and consequently has no significant influence on magnetic anisotropy constants.

The total free energy density of the system with the external field H is considered as the following formula7:

where the first term is the Zeeman energy, is the unit vector of the magnetic vector and Ms is the saturation magnetization of Fe (taken as the bulk value 1.74 × 106 A/m); the second and third terms are cubic magnetocrystalline anisotropy energy, αi represents the directional cosines of the magnetic vector with respect to the cubic axes [100], [010] and [001], K1 and K2 are the first two cubic magnetocrystalline anisotropy constants; the last three terms sequentially refer to the uniaxial magnetic anisotropy energy and surface magnetic anisotropy energy and out-of-plane demagnetization energy. Ku, Kd and Ks are the corresponding magnetic anisotropy constants. The unit vector with its orientation along the step direction represents the direction of the easy axis of the uniaxial magnetic anisotropy. and are the unit vectors normal to vicinal (111) film plane and the (111) plane, respectively. It should be noted that the unit vector is perpendicular to the vicinal plane, which is different from a simple flat thin (111) crystal plane with its hard axis of the out-of-plane.

Figures 2 (a) and (b) present the angular dependence of the first- and second-order magnetocrystalline anisotropy energy terms in the Fe(111) plane along [11-2] with various miscut angles, where K1 = 4.5 × 104 J/m3 and K2 = 0.05K116, respectively. We can find that the K1 energy term is invariable (solid line circle in Fig. 2(a)) and the K2 energy term is six-fold symmetry in exact Fe(111) plane, i.e. miscut angle β = 0°. However, the K1 energy term can be changed to a four-fold symmetry by a slight misorientation from (111) plane, i.e. β ≠ 0°. Figure 2(b) demonstrates that the symmetry of the K2 energy term keeps unchanged.

Figure 2
figure 2

The angular dependence of magnetocrystalline anisotropy energies.

First- (a) and second- (b) order magnetocrystalline anisotropy energy terms for various miscut angles β, respectively.

Full size image

Since the magnetization reversal process is largely governed by the symmetry, magnitudes and directions of the competing magnetic anisotropy energies, the symmetry of magnetic anisotropy energy is usually probed by magnetic hysteresis loop. The MOKE hysteresis loops at various angles φH between the [-110] axis and magnetic field H, indicate that the easy axis is perpendicular to the step direction, φH = 90° (Fig. 3(a)). Similar phenomena have been reported in the system Fe/W(001) or Au/Co/Cu/Si(111), which have been explained by the step-induced anisotropy31,32. Unfortunately, owing to the small coercivity (<10 Oe) in the sample, only the two-fold symmetry in remanence and coercivity can be confirmed from figures 3(b) and 3(c), respectively. The contribution of magnetocrystalline anisotropy constants K1 and K2 cannot be determined from MOKE measurements.

Figure 3
figure 3

The typical hysteresis loops and angular dependence of in-plane magnetic coercivity and remanence.

Experimental hysteresis loops at 0 and 90 deg. (a), angular dependence of in-plane magnetic coercivity (b) and remanence (c) by means of MOKE.

Full size image

In order to figure out the magnetocrystalline anisotropy constants K1 and K2, we carried out the AMR measurements. We found that the resistances of Si substrate with and without iron silicide buffer layer, which are almost the same values, are quite larger than the resistance of Fe ultrathin film. Furthermore, the Si substrate and iron silicide buffer layer have no contribution to AMR. Therefore, the metallic Fe single crystal film gown on iron silicide buffer layer and Si(111) surface provides an ideal system to perform AMR measurements. In the case of Fe single-crystalline system, the AMR can be expressed as20,21,22,23,24,25,26:

where φM is the angle between the Fe magnetization MFe and the current flow I, and is the resistance at φM = 0° and φM = 90°, respectively.

Figure 4(a) shows the angular dependence of the in-plane AMR with different applied fields. The external magnetic fields are larger than saturation field to guarantee a true single-domain rotation and eliminate the ordinary magnetoresistance effect. During rotation of the sample, the AMR values show an oscillated behavior between the maximum value and minimum value , respectively. However, owing to the magnetic anisotropy, MFe is no longer kept along with the external field H during rotation, i.e. φM < φH. Therefore, the AMR curves do not follow the cos2φH relationship. The correlation between φH and φM can be obtained from Fig. 4 (a) and plotted in Fig. 4 (b).

Figure 4
figure 4

The in-plane AMR curves at different curves and the correlation between φH and φM.

Angular dependence of the in-plane AMR (a) and the correlation between φH and φM at different fields (b).

Full size image

On the basis of the angle difference between φH and φM, we can further calculate the magnetic torque curves from Fig. 4(b) at different external fields. In order to compare magnetic torques at different fields, the normalized magnetic torque was introduced. As shown in figure 5(a), the normalized magnetic torque curves exhibit different shapes with different external field H. In equilibrium state, the torque acting on MFe due to H is equal in magnitude to the torque due to the magnetic anisotropies of the sample. Since the demagnetization field is normal to the Si(111) plane, its contribution to the magnetic torque is zero. According to Eq.(1), the normalized magnetic torque can be written as:

where , β is the miscut angle of the substrate.

Figure 5
figure 5

The normalized magnetic torque curves.

Normalized magnetic torque curves superposed by the first- and second-order magnetocrystalline anisotropies and uniaxial anisotropy at different fields (a) and the normalized torque contributed only by the first- and second-order magnetocrystalline anisotropies at field of 1600 A/m (b), the solid lines are fitting curves. For comparison, the normalized magnetic torque curves were also plotted in Figure 5(a).

Full size image

Although the value of Ks(~106 J/m3) is far larger than that of Ku(~102 J/m3) for ultrathin Fe film15,16, we can calculate from Eq.(3) that the value of torque contributed by Ks is at least two order of magnitude smaller than that contributed by Ku. Therefore, the contribution of surface anisotropy constant to the torque can be neglected.

It can obviously from Eq.(4) that the magnetic torque shows a superposition of two-, four- and six-fold magnetic anisotropies from the step-induced uniaxial magnetic anisotropy Ku, the first-order magnetocrystalline constant K1 and the second-order magnetocrystalline anisotropy constant K2, respectively. The two-fold symmetry disappears gradually with increasing external field H, suggesting that the strength of Ku is very weak. Therefore, in order to distinguish the contribution from Ku, the external field H should be kept slightly larger than the saturation field.

From Eq.(3), we can obviously find that the normalized torque l(φM) is significantly affected by the substrate's miscut angle β. The tendency of the anisotropy energy is complicated. We can find that the four-fold anisotropy energy changes significantly (Fig. 2(a)), while the six-fold anisotropy energy almost does not change with the miscut angle β (Fig. 2(b)). In the case of β = 0.0°, the K1 term is zero. Usually the miscut angle of the substrate cannot be neglected and thus the contribution from the first-order magnetocrystalline anisotropy constant in vicinal (111) plane must be taken into account.

In order to investigate the tiny variation of miscut angles on the fitting parameters, Figure 6 illustrates the fitted magnetic anisotropy constants for various miscut angles β from −0.30° to 0.30°. It is noteworthy that a tiny variation of miscut angles β has no effect on the values of K2 and Ku(Figure 6(a)), whereas significantly affects the fitted values of the first-order magnetocrystalline anisotropy K1(Figure 6(b)). Since the global AMR properties are measured for the whole sample, the use of the mean miscut angle of Si(111) of about 0.10° is reasonable. The fitted value of K1 = 3.4 × 104 J/m3 is comparable with the value of K1 = 4.5 × 104 J/m3 for bulk bcc-Fe.

Figure 6
figure 6

The fitted magnetic anisotropy constants K2 and Ku (a) and K1 (b) for various miscut angles β from −0.30° to 0.30°.

Full size image

The AMR results are consistent with the fitting results from FMR, where K1 = 4.4 × 104 J/m3, K2 = 2.2 × 103 J/m3 and Ku = −5.9 × 102 J/m3 for 45 ML Fe film on Si(111)16. For comparison, we also measured the 45 ML Fe sample in Ref. 16 by FMR to cross-check the measured anisotropy constant obtained by AMR. As shown in figure 5(a), the magnetic anisotropy constants K1 = 4.4 × 104 J/m3, K2 = 2.1 × 103 J/m3 and Ku = −1.1 × 103 J/m3 can be obtained. Both AMR and FMR give almost same values of K1 and K2, while the absolute value of Ku obtained by AMR are slightly larger. A careful comparison between these two techniques to measure the magnetic anisotropy constants is in progress.

The negative value of Ku suggests that the easy axis is perpendicular to the step direction, which is in good agreement with the hysteresis loops (Fig. 3 (a)). By using the magnetic anisotropy constants, the angular dependence of coercivity and remenance were also simulated in term of coherent rotation magnetization reversal, as illustrated in Figs. 3(b) and (c), respectively. We can observe that the calculated remanence is consistent with experimental one, whereas the calculated coercivity deviates the experimental one significantly in the easy axis direction. The significant deviation implies that the magnetization reversal is not governed by coherent rotation and consequently, magnetic hysteresis loop cannot provide a detailed symmetry of magnetic anisotropy energies.

The contribution of K1 and K2 to magnetic torque is about one order of magnitude smaller than that of uniaxial magnetic anisotropy constant Ku. In order to separate their contributions, Fourier analysis and inverse Fourier transform are used to analyze the torque curve. If we deduct the contribution of the uniaxial magnetic anisotropy constant Ku to the magnetic torque, it is obviously shown in figure 5(b) that the normalized magnetic torque curve is the superposition of a four-fold and a six-fold anisotropy contributed only from first- and second-order magnetocrystalline anisotropy constants, respectively.

Discussion

We present the MOKE and AMR measurements of Fe single crystal film on 0.1° vicinal Si(111) substrate with atomically flat ultrathin p(2 × 2) iron silicide as buffer layer. Unfortunately, owing to the small coercivity (<10 Oe) in the sample, only the two-fold symmetry in remanence and coercivity can be observed, while the contribution of magnetocrystalline anisotropy constants K1 and K2 cannot be determined from MOKE measurements. On the other hand, the AMR results demonstrate that the symmetry of magnetocrystalline anisotropy energy changes from the six-fold to a superposition of six-fold, four-fold and a weakly uniaxial contribution due to the tiny misorientation from Fe(111) plane. Although the use of AMR to measure the magnetic anisotropy was introduced long time ago20,21,22,23,24,25,26, to our knowledge, a precise determination of various magnetic anisotropy constants of Fe(111) film on Si(111)-7 × 7 surface with so small miscut angle was not reported in literature. The fitted value of the first-order magnetocrystalline anisotropy K1 is significantly influenced by the tiny variation of miscut angles β. On the other hand, the values of K2 and Ku are unchanged. Our work suggests that the AMR measurements can precisely separate the detailed contributions of various magnetic anisotropy constants of single crystalline Fe ultrathin film grown on vicinal Si(111) surface.

Methods

The sample was prepared on Si(111) wafers with nominally miscut angle of 0.1° along [11-2] using an ultrahigh vacuum molecular beam epitaxial chamber (MBE) equipped with the scanning tunneling microscope(STM) and low-energy electron diffraction(LEED). The base pressure of MBE is kept around 2 × 10−10 mbar and all the experiments were conducted at room temperature. After a well-established procedure15,16, the well-defined reconstructed Si(111)-7 × 7 surface was obtained. The buffer layer was deposited on the wafers for 1.5 ML of Fe (99.999% purity) heated by e-beam bombardment with a deposition rate of 1.5 ML/min, then annealed at 700 K for 10 min. This procedure gives a highly ordered 2 × 2 periodic iron silicide structure to prevent the Fe/Si intermixing6. Fe film with thickness of 21 ML was deposited on the iron silicide template. The STM (VT-STM) measurements were performed at the Si substrate, iron silicide template and the Fe film. A non-magnetic NaCl with thickness of 14 ML was deposited on the sample as a capping layer to protect samples oxidization.

The MOKE measurements were carried out at room temperature and described in detail elsewhere15,16. The home-made AMR setup consists of a Wheatstone bridge, a Lock-in amplifier (Stanford Research Systems SR830 DSP), a temperature controller (Stability < 0.0012°C/h) and a rotational sample stage. Magnetic field is provided by a Helmholtz coil. In the experiments, a sufficiently large and stable field is applied to guarantee a true single-domain behavior of the specimen. The application of Wheatstone bridge and highly stable temperature controller ensures the sensitivity of AMR better than 0.01% in the entire measurements. The sample size is 3 mm × 5 mm for AMR measurements, which were performed with a standard four-point method.