Introduction

Because fluorescence probes and proteins have been designed extensively to be specific to particular cellular functions such as signal transduction and gene expression within cells, fluorescence microscopy has become an invaluable tool in biology. However, a primary limitation of fluorescence microscopy is that it cannot resolve sub-cellular structures beyond the diffraction limit1. In many biological experiments, this resolution limit is not satisfactory for investigating the structures and functions of macromolecules. In order to address this problem, super-resolution far-field fluorescence microscopy has been investigated extensively for the past decade2,3,4,5,6,7,8. A foundational concept behind this super-resolution microscopy is to exploit non-linear optical phenomena. For example, in stimulated emission depletion (STED) microscopy2, a Gaussian-shaped excitation beam and a red-shifted doughnut-shaped STED beam are used to sharpen the effective point spread function (PSF) by quenching excited fluorophores at the rim of the PSF. Unlike STED, stochastic optical reconstruction microscopy (STORM) and photoactivated localization microscopy (PALM)7,8 are based on the single molecule imaging principle4,5,6 by localizing the sparsely activated fluorophores using photoswitchable probes. However, considering that the large inventories of the existing fluorophores or fluorescent proteins are not photoswitchable, a new super-resolution imaging architecture that is compatible with the conventional experimental protocols and fluorescence probes should be developed in order to increase the use of super-resolution microscopy in biological experiments.

The structure illumination microscopy (SIM)9 partially fulfills this need because it improves the optical resolution by synthesizing the extended aperture from multiple images with distinct spatial modulations. Moreover, the resolution of the SIM can be further enhanced using the non-linear dependence of the emission rate of fluorescent probes on the intensity of the excitation laser3 at the expense of the increased possibility of cell damage resulting from the higher intensity of the excitation laser. Although the basic form of the SIM remains extremely useful due to its compatibility with standard probes and experimental protocols, it requires sophisticated optical alignment and relatively high laser intensity in order to generate precise illumination patterns.

Recently, in an attempt to alleviate the requirements of the SIM, structured illumination microscopy using speckle illumination has been developed by our research group10,11 and others12. The key concept of these two approaches is to replace the patterned illumination with unknown speckle illuminations and to compensate for the blindness of the illumination patterns by exploiting the statistical properties of the speckle illuminations. For example, we exploited the fully developed speckle patterns being nearly incoherent10,11, whereas the authors in Reference12 assumed that the temporal average of speckle illumination is roughly homogeneous over the specimen. However, in many experimental conditions, these assumptions often fail, which results in degraded performance. Therefore, in this paper, we develop a new super-resolution speckle illumination microscopy without any assumptions of the statistical properties of the speckle illumination. Instead, we exploit the minimal requirement that is common for all super-resolution imaging: the locations of the fluorescent probes do not vary during image acquisition.

Recall that the fluorescent emission intensity measured at position r at time t is given by

where hD(·) denotes the diffraction-limited PSF of the detector optics and J(r′, t) denotes the emission photon flux at r′ through an excitation of fluorophores at time t. Here, the photon flux (J) is determined by

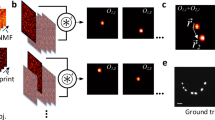
where χ(r′) is the unknown fluorescent probe density at r′ and Φ(r′, t) denotes the unknown optical flux at r′ that originated from an illumination beam as well as a fluorescent emission from the neighboring fluorescent probes. As shown in Figure 1, for speckle illuminations, the optical flux (Φ(·, t)) that results from the speckle illumination varies randomly along time t, whereas the locations of the fluorescent probes (χ(·)) do not vary as long as the specimen is stably mounted during the acquisition. This implies that regardless of the illumination changes, the product χ(r′)Φ(r′, t) should have the same spatial support and have non-zero values for all t in positions where χ(r′) ≠ 0. Then, the fluorescent emission lights excited by multiple speckle patterns are measured using a diffraction-limited lens. Using a reconstruction algorithm under joint support constraint, our goal is to obtain the locations and magnitudes of the fluorophores from the multiple speckle illuminated fluorescent microscopy images.

Figure 1
figure 1

Principle of joint support recovery for super-resolution microscopy using speckle illumination.

The fluorescent emission lights excited by multiple speckle patterns are measured through a diffraction-limited lens. Using a nonlinear reconstruction algorithm under a joint support constraint, we can obtain the locations and magnitudes of the fluorophores from the multiple speckle illuminated fluorescent microscopy images.

Full size image

The image recovery from multiple measurements under the aforementioned joint support constraint has been studied extensively in the signal processing community. Indeed, these types of problems are often called the multiple measurement vector (MMV) problems13,14,15,16 and a variety of advanced mathematical algorithms and theories to address the problems exist16,17,18,19. Among these algorithms, we implement the multiple sparse Bayesian learning (M-SBL) algorithm17 due to its well-known noise robustness and high performance. More specifically, M-SBL formulates the recovery framework using an empirical Bayesian setup in order to exploit the support for the unknown signals being common during multiple measurements acquisition (see Supplement for more details of the M-SBL). Mathematically, it has been demonstrated that the common support constraint improves the resolution compared with the conventional recovery algorithm16. This is the key clue for improving the resolution beyond the diffraction limit in our proposed method.

Results

Quantitative analysis

First, we performed a numerical simulation as shown in Figure 2. See the Methods section for the detailed parameter settings used in the numerical study. From 300 speckle illumination images, the proposed method resolved two lines with distance at full-width at half-maximum (FWHM)/3 while the conventional image and its deconvolution image using the standard Lucy-Richardson method cannot distinguish these two lines. The results indicate that our proposed method can achieve up to threefold resolution improvement over the diffraction limit.

Figure 2
figure 2

Numerical resolution phantoms.

The first column images correspond to the ground truth images of the resolution phantoms. Conventional wide-field images, standard Lucy-Richardson deconvolution images and our reconstruction results are presented in the next three columns, respectively.

Full size image

Next, we prepared an equiangular radial nanopattern as shown in Figure 3 (see the Methods section for details of the sample preparation). We took a sample with 500 random realizations of the speckle illumination. Compared with the conventional wide-field image in Figure 3(d) and the Lucy-Richardson deconvolution microscopy result in Figure 3(c), the reconstruction using the proposed method in Figure 3(b) exhibts well-resolved lines with a minimum distance of 80 nm. Furthermore, the reconstruction result is well matched to the SEM image in Figure 3(a).

Figure 3
figure 3

Radial nanopattern with a minimum distance of 80 nm: (a) detail of a SEM image, (b) reconstruction using the proposed method from the 500 speckle illuminations, (c) deconvolution image using the Lucy-Richardson algorithm and (d) the diffraction limited image.

Full size image

Finally, multiples patches from randomly scattered and aggregated 50 nm nanoparticles were used and are presented in Figure 4 (see the Methods section for details on the sample preparation). As shown in the second row of Figure 4, the reconstruction results using the proposed method revealed a clearer configuration of the nanoparticles than that from the diffraction-limited images (third rows in Figure 4) and our results were comparable with the SEM images (first row in Figure 4). As can be seen from Figure 4, empty spaces exist around or between the nanoparticles and they have various distances, as marked. Our proposed method successfully resolved these spaces.

Figure 4
figure 4

Reconstruction results of randomly scattered nanoparticles.

First row: scanning electron microscope (SEM) images. Second row: proposed super-resolution images from the 500 speckle illuminations. Third row: diffraction-limited wide-field microscopy images.

Full size image

Super-resolution imaging of sub-cellular structure

We also applied our method to real bio-samples. The outer membrane of the mitochondria of a HeLa cell was stained with a fluorescent dye (Alexa 488)(see the Methods section for details of the sample preparation). Then, we imaged the sample with 500 random realizations of the speckle illumination. As shown in Figures 5(a) to 5(c), our method exhibits much clearer mitochondria structures, whereas the diffraction-limited conventional image and its deconvolution image failed to resolve them. In the close-up images (Figures 5(d) to 5(i)), our method revealed better boundary profiles of the mitochondria outer structure than the other images.

Figure 5
figure 5

Mitochondria structure in the HeLa cell with its outer membrane stained with a fluorescent dye (Alexa 488): (a) conventional wide-field image, (b) deconvolution image of (a), (c) proposed super-resolution image from 500 speckle illuminations, (d,f,h) detail images of the dashed line boxes in (a–c), respectively and (e,g,i) detail images of the solid line boxes in (a–c), respectively.

The scale-bars are 2 μm in (a–c) and 500 nm in (d–i).

Full size image

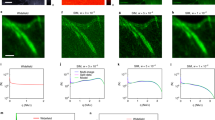
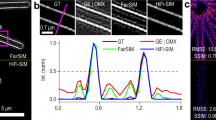
Next, the sub-cellular structures such as microtubules in the HeLa cell were imaged using a 488 nm argon laser as shown in Figure 6. Microtubules are rope-shaped polymers of tublins and the diameter of the microtubule is known as 25 nm. The microtubules were stained with Alexa488 and 400 speckle images were taken. As shown in Figures 6(a) and 6(b), the microtubule structure is clearly resolved in the proposed method compared with the diffraction-limited conventional image. In the close-up images, i.e. Figures 6(c) to 6(d), the proposed method successfully resolves two adjacent microtubule lines that are 84 nm apart, which is a threefold resolution improvement over the diffraction limit.

Figure 6
figure 6

Microtubule structure in the HeLa cell stained by a fluorescent dye (Alexa 488): (a) diffraction-limited image; reconstruction images using (b) the Lucy-Richardson deconvolution method and (c) the proposed method from 500 speckle illuminations; and (d) line profiles of the dotted areas in (a–c).

The light-blue line is from a diffraction-limited image; the dark blue line is from the Lucy-Richardson deconvolution; the red line is from the proposed method. Note that the proposed image can resolve a distance of 84 nm, which corresponds to threefold improvement in the resolution over the diffraction limit. The scale-bars are 500 nm in (a,b) and 250 nm in (c,d).

Full size image

Discussion

In this paper, we developed a novel far-field super-resolution microscopy using random speckle illumination and joint support recovery. In order to generate the random illumination, quasi-random speckle patterns from a coherent source were used. We performed experiments using the simulated data, real samples of radial nanopatterns and nanoparticles as well as bio samples using standard probes and experimental protocols. A spatial resolution improvement more than threefold was achieved and a distance of 84 nm distance was resolved in a real bio-sample.

The proposed method has many unique advantages. First, unlike the SIM, a sophisticated control for the generation of illumination patterns is not required because the randomness of the illuminations is exploited rather than pre-designed structures. Second, unlike the blind SIM that assumes that the average the speckle illumination is homogeneous across the specimen20, the proposed method exploits the algebraic property of the joint support, which is the minimal assumption for all super-resolution microscopy, but it can still improve the resolution over the blind SIM despite the underlying statistics. Third, a high power laser that generates a saturated emission is not required, as the non-linearity of the proposed method results from the joint support recovery rather than optical phenomenon. Accordingly, the unique characteristics of the proposed method will be beneficial to many standard bio-imaging experiments.

Methods

Numerical simulation

For a quantitative analysis of the proposed method, we performed experiments using simulated data, nanopatterns and nanoparticle samples. In a simulated experiment as shown in Figure 2, parallel lines with the distances at the full-width at half-maximum (FWHM), FWHM/2 and FWHM/3 of the diffraction limit, were illuminated by a series of 300 speckle illuminations. The average number of emitted photons was set to 22/nm2. The images were obtained after blurring by a Gaussian PSF with 270 nm FWHM and 100 background photons were added to each CCD pixel with a pitch size of 45 nm. The measurement noise was modeled as a Poisson noise with a small additive Gaussian readout noise with a variance of 3. In order to simulate the diffraction-limited speckle illuminations, we first generated fully developed speckles21 where both real and imaginary parts of the electromagnetic fields of the speckles follow zero-mean Gaussian distributions with the same variance. Then, the fully developed speckles are low-pass filtered with the Gaussian PSF whose FWHM is the same as that of the detector PSF under the assumption that the imaging system is an epi-fluorescence microscopy.

Equiangular radial nanopatterns

The nanofabrication procedures are as follows. First, hydrogen silsesquioxane (HSQ, negative tone electron-beam resist) and Rhodamine 6 G dyes were mixed. Then, the mixture was spin-coated on a glass substrate. The sample was exposed to an e-beam after soft baking. The unexposed region was dissolved in the following development, while the exposed region (radial nanopatterns) remained on the substrate. Finally, equiangularly divergent lines with 100 nm in line width and height were obtained with a minimum gap of 80 nm as shown in Figure 3(a).

Nanoparticles

For quantitative analysis, we prepared specimens of fluorescent silica shelled nanoparticles with diameters of 50 nm (CELL-STALKER™CSR, Biterials) that contained Rhodamine B isothiocyanate (RITC, Ex/Em = 515 nm/578 nm). The SEM and fluorescence microscopy images of the same regions were also obtained. In order to achieve this, we used μ-Dish 35 mm Grid-500 (Ibidi©, Germany), which has a 500 μm two-dimensional grid array with lettered and numbered fields. When we acquired the fluorescence image on the dish, the position of the grid was also recorded. After acquiring the fluorescent images, the recorded grid position in the SEM was found and then the SEM images of the same regions were acquired. In order to achieve uniform dispersion of the nanoparticles, the substrate was rinsed with distilled water, dried with filtered dry air and treated with oxygen plasma (60 seconds at medium power in a Harrick Scientific plasma cleaner) in order to leave a hydrophilic surface with a low contact angle. Then, the substrate was mounted vertically and the diluted nanoparticle solution flowed over the substrate (1:9, nanoparticle (2 mg/ml) in DI water) through pipetting it.

Cell preparation

Antibodies against cytochrome c and TOM20 (for mitochondria) were purchased from BD Biosciences. A microtubule marker (AE-8) was purchased from Santa Cruz Biotechnology. Alexa Fluor 488-conjugated goat anti-mouse and goat anti-rabbit IgG were purchased from Molecular Probes. HeLa cells were grown in Dulbeccos complete medium (JBI) supplemented with 10% heat-treated fetal calf serum (Invitrogen), 100 U/mL penicillin and 100 g/mL streptomycin. For the immunostaining, the cells grown in the culture dish with cover glasses were fixed with 4% paraformaldehyde for 15 min at room temperature, permeabilized with 0.15% Triton X- 100 in PBS for 15 min at room temperature and then blocked with 3% bovine serum albumin in PBS for 45 min at room temperature. The cover glasses with cells were incubated for 2 hr with the primary antibodies indicated in the figures. After washing with PBS, the glasses were incubated for 1 hr with the secondary antibody with the fluorescent material. The cover glasses were mounted with a fluorescent mounting medium (Dako).

Imaging system

As shown in Figure 7, an Olympus IX71 microscopy was used after modifying the epi-fluorescence illuminator: a 488 nm Argon laser (Stellar-Pro-L 488/100, Modu-Laser) and a low power 532 nm continuous wave diode pumped solid state laser (SDL-532-500, Shanghai Dream Lasers Technology) were used to excite the samples through an ND filter. The excitation lasers were combined with a dichroic mirror (DM) (LM01-503, Semrock) and then one excitation laser can be selected using a mechanical shutter. The excitation laser was illuminated onto the rotatable diffuser through an expansion lens (herein, LI = −25 mm) and the scattered light collected by a pair of lens (L1 = 100 mm and L2 = 100 mm) was focused on the back focal plane of the objective lens (O), which was a 100× oil-immersion lens with 1.30 NA (UIS2, Olympus) reflected by dichroic mirror (DM) (FF405/496/560/651, Semrock). Telescope lenses L1 and L2 are achromatic lenses (Thorlabs, AC254-200-A, f = 200 mm). The fluorescence emission light was collected with an identical objective lens (O) and the collected light was filtered with a dichroic mirror (DM) (FF405/496/560/651, Semrock) and an emission band-pass filter (F2) (FF01-422/503/572-25, Semrock). Using a function generator (AFG310, Tektronix), we controlled the synchronization between the rotation of the diffuser (D1) and the imaging acquisition time of the electron-multiplying CCD (EMCCD) camera (D2) (Luca-S, Andor), which had a pixel size of 10 μm. The customized diffuser (D1) consists of a rotatable diffusive disc with a rough surface on a motorized rotation stage. The diffusive disc is also coated with TiO2 nanoparticles mixed with liquid glue. The rotation speed of the diffuser was one rotation per 500 pulses and each pulse of the diffuser rotation is synchronized with a camera acquisition frame. In front of the camera, the additional magnification lens (L3, 1.6× magnification) and adapter for the IX71 (U-TV1X-2 with U-CMAD3, Olympus) were used. The quantum efficiency (QE) of the EMCCD camera in our experiments has approximately 50% and the CCD acquisition rate was set to 10 Hz in all the experiments.

Figure 7
figure 7

Experimental image system constructed through modifications of the epi-fluorescence microscopy.

The excitation laser (532 nm or 488 nm) is combined by the dichroic mirror (DM1) and scattered by the diffuser (D1) in front of the illumination optics (LI, L1 and L2); then, the scattered light is focused on the sample plane by the objective lens (O). The emission fluorescence signal returns through the dichroic mirror (DM2) and the emission filter (F); it is also magnified by the tube lens (L3) in front of an EMCCD camera (D2).

Full size image

We prevented axial directional drifts using a nanometer scale positioning system (Nano-F200S, Mad City Labs) and feedback control system. The feedback control was implemented with additional reference lights such a HeNe laser or near infrared laser. The reference light is combined with the excitation laser between two telescope lenses and is reflected from the boundary surface of the oil and cover glass; then, the reflected light is passed through the relay lenses and cylindrical lens and then imaged by the extra camera. Due to the astigmatism of the cylindrical lens, the reference images of the reflected light corresponding to the axial space between the objective lens and cover glass can be obtained. According to the reference images, we created a customized feedback control system, which provided a few tens of nanometers stabilization performance. While the system maintains the axial space between the objective lens and cover glass, the focal plane of the objective lens can be maintained for the total acquisition time.

Image reconstruction

In order to begin the image reconstruction, the PSFs must be estimated. For the simulated data, our joint sparse recovery algorithm used the same Gaussian PSF of 270 nm FWHM that was used to generate the data. In the real experiments, the measured PSFs were used: for example, the measured Gaussian PSF of 270 nm FWHM was used for the 488 nm excitation laser (mitochondria in Figure 5 and microtubule in Figure 6, respectively). For the 532 nm excitation laser (i.e. the radial nano pattern in Figure 3 and the nano-bead experiments in Figure 4), the measured Gaussian PSF was 300 nm, which was used for joint support recovery.

For the joint sparse recovery algorithm, we used the multiple sparse Bayesian learning (M-SBL) algorithm due to its proven effectiveness for joint support recovery (See the Supplement for a more detailed description of the M-SBL). In order to reduce the computational complexity, each image frame was divided into overlapping 1.2 μm × 1.2 μm blocks and the M-SBL was applied to each block after subtracting its temporal average. In order to avoid boundary artifacts, the central 1 μm2 area from each reconstructed 1.2 μm × 1.2 μm image was used. In order to consider the multiple overlapping blocks when generating the final pixel values in a gradual manner, a 2D cosine weighting was used for each block, where the weighting factor for the cosine weighting was designed such that its value was one at the center and zero in the four corners. Then, the final image was generated as a sum of the cosine weighted multiple 1 μm2 area. In order to accelerate the overall execution time, the M-SBL was implemented on an Nvidia Tesla C1060 graphic processing unit (GPU) using Compute Unified Device Architecture (CUDA) programming. In order to suppress the off-focus fluorescence signal in the biological sample (Figures 5 and 6), the fluorephores at the in-focus locations and three times broader off-focus PSFs locations were reconstructed together, from which the off-focus fluorphores were excluded in the final image.

Depending on the samples, the reconstruction pitches were set equal to the CCD pitch (Figures 2, 4 and 5) or one third of the CCD pitch (Figures 3 and Figure 6). The reconstruction time of the proposed method, e.g. Figure 2, was approximately 2.9 sec for 1 μm2 area reconstruction using 300 speckle image frames with our GPU implementation.