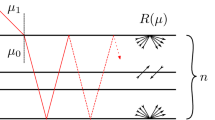
Abstract
An accurate and efficient solution of the radiative transport equation is proposed for modeling the propagation of photons in the three-dimensional anisotropically scattering half-space medium. The exact refractive index mismatched boundary condition is considered and arbitrary rotationally invariant scattering functions can be applied. The obtained equations are verified with Monte Carlo simulations in the steady-state, temporal frequency and time domains resulting in an excellent agreement.
Similar content being viewed by others
Introduction
In many research fields the radiative transport equation (RTE) is the fundamental equation for describing particle transport like neutron propagation in reactor physics1 or photon propagation in atmospheric physics, in astronomy, or in biophotonics2,3,4. For quantitative investigations of the photon transport in biological media the RTE is used for all scales, i.e. for macroscopic, mesoscopic and microscopic applications5, where interference effects don't have to be taken into account. For example, it is applied for non-invasive investigations of the light propagation in the human brain, in small animals, or for quantitative microscopy6,7,8,9,10.
The RTE is usually solved with numerical methods. In the case of isotropic scattering half-space media the RTE can be solved analytically as it is reported in the publications11,12,13,14. In the field of biophotonics mainly the Monte Carlo (MC) method is applied15. Due to the long simulation time needed with numerical methods until accurate results are received the RTE is often approximated by the diffusion equation. Within the diffusion approximation (DA) analytical solutions can be obtained for several geometries16,17,18,19. However, it is well-known that the DA fails in the high spatial and temporal frequency domain (TFD) resulting in a breakdown of the diffusion theory for small distances to sources and boundaries as well as for short time values. The fact that adequate analytical solutions are still rare but of great interest is underlined by many recently published articles which present diffusion theory based models20 or approximated solutions of the RTE21.
In this article we report on radiative transport solutions for describing the propagation of photons in the three-dimensional anisotropically scattering half-space medium. The effect of Fresnel reflection at the interface which is present in nearly all measurements is also considered. The semi-infinite geometry is abundantly used in all three measurement domains16,17,22,23. The accuracy of the derived equations is demonstrated in the figures below by comparisons with Monte Carlo simulations showing an excellent agreement.
Results
In the following we give an overview regarding the applied analytical approaches and the appropriate numerical calculation steps for obtaining the proposed radiative transport solution. We start with the derivation in the TFD where the quantities of interest are the demodulation and the temporal phase shift between the injected specific intensity and the measured signal.
The specific intensity caused by a sinusoidally modulated pencil beam

which enters the boundary of the semi-infinite scattering medium z ≥ 0 becomes G(r, ŝ, t) = G(r,ŝ) exp(iωt), where  and
and  is the angular modulation frequency. The complex amplitude obeys the RTE2,3
is the angular modulation frequency. The complex amplitude obeys the RTE2,3

where μt = μa + μs + iω/c is the frequency dependent total attenuation coefficient, μa the absorption coefficient, μs the scattering coefficient, c = c0/n is the velocity of light in the scattering half-space with refractive index n. The detection of the specific intensity takes place at the spatial position  , whereas the unit vector
, whereas the unit vector  specifies the direction of the photon propagation and f(ŝ·ŝ′) is the scattering phase function which is normalized to unity. The exact boundary condition (BC) corresponding to a pencil beam which enters the half-space z ≥ 0 is defined in the angular domain
specifies the direction of the photon propagation and f(ŝ·ŝ′) is the scattering phase function which is normalized to unity. The exact boundary condition (BC) corresponding to a pencil beam which enters the half-space z ≥ 0 is defined in the angular domain  and is given by
and is given by

where R(μ) is the Fresnel reflection coefficient12 and μ = cosθ. Here Green's function in the frequency domain is separated into its ballistic and diffuse contribution3 according to G(r,ŝ) = G(r,ŝ) + I(r,ŝ). By substituting this ansatz in (2) we obtain the first RTE

whose solution under consideration of the BC (3) yields the ballistic component

where Θ(z) denotes the Heaviside step function. Taking into account this component we obtain the second RTE for the diffuse part

which has to be solved subject to the BC

The particular solution of (6) can be evaluated rapidly by performing a similarity ansatz. It can be shown that

with Hankel transformed coefficients

is a complete and exact solution of the RTE (6) for appropriate spectral components Ilm(q) = (−1)mIl,−m(q). Moreover Ylm(θ, χ) with χ = φ − φρ are the spherical harmonics (SH) and Jm(x) are the Bessel functions of the first kind. Inserting (8) together with (9) in (6) and making use of recurrence relations for the SH and the Bessel functions leads to the following set of linear equations labeled by l = m, m + 1, … for m = 0, 1, … according to

with the quantities σl = μt − flμs. The remaining quantities are given by  , blm = cl,−m and
, blm = cl,−m and  . The expansion coefficients of the scattering phase function are defined as
. The expansion coefficients of the scattering phase function are defined as

where Pl(x) are the Legendre polynomials. The system of linear equations (10) written in matrix notation becomes

Now the solution to the boundary-value problem (7) can be achieved by considering additionally the general solution to the homogeneous RTE. In our recent study26 we solved the homogeneous problem in the steady-state domain by applying the method of rotated reference frames24,25. Although the obtained solution is formally exact its successful application is impossible for several situations of high practical importance due to numerical shortcomings. Therefore, we reconsidered the homogeneous problem in the TFD and obtained the following complete new result

where

with

and αi = Re(ξi). The eigenvalues ξi and the eigenvector components  follow as solution of the generalized eigenvalue problem
follow as solution of the generalized eigenvalue problem

which can be translated into a standard eigenvalue problem because det(S + iqB) ≠ 0. The characteristic equation of (16) is given by

where λi are the eigenvalues of the matrix (S + iqB)−1 A. Note that in the steady-state domain which entails that ω = 0 the eigenvalues ξi = 1/λi are strictly real-valued. The corresponding nontrivial solution |ui(q)〉 ≠ 0 to the eigenvalue ξi is that which is given by the eigenvector to λi. The general solution to the RTE (6) for the semi-infinite geometry is now obtained via superposition of the homogenous and particular part.
Next, we apply the generalized Marshak BC24,25,27 for satisfying equation (7) and to determine the unknown constants Ci(q) within the homogenous solution. At this stage the solution to the RTE (6) for the semi-infinite geometry is completed. In view of diagnostic and therapeutical applications the back-scattered light R(ρ) = − ∫ μI(ρ, 0, ŝ)dŝ and the internal fluence Φ(r) = ∫ I(r, ŝ)dŝ are quantities of particular interest. By making use of the derived specific intensity as well as of the orthogonality relation  , we find the following expressions for the reflectance
, we find the following expressions for the reflectance

and for the fluence in z ≥ 0

The above derived solution can be evaluated for an arbitrary angular frequency. Therefore, we can reconstruct the time-resolved impulse response or Green's function for the diffuse specific intensity according to

The frequency dependent coefficients from system (10) satisfy the condition  . In addition, the real and imaginary parts of I(r, ŝ, ω) are connected by the Hilbert transform so that it is sufficient to invert e.g. only the real part. Green's function of the time-dependent RTE for the semi-infinite medium is complete by adding the ballistic contribution
. In addition, the real and imaginary parts of I(r, ŝ, ω) are connected by the Hilbert transform so that it is sufficient to invert e.g. only the real part. Green's function of the time-dependent RTE for the semi-infinite medium is complete by adding the ballistic contribution  .
.
The derived solutions to the RTE are verified by comparisons with MC simulations28 in three different measurement domains. The lateral intensity profile of the collimated incident beam is modeled by a Gaussian function according to S(ρ) = 2/(πη2) exp(−2ρ2/η2), where η denotes the radius of the beam. Due to the convolution theorem we have to multiply the right-hand side of system (12) with the Hankel transformed distribution S(q) = exp(−q2η2/8). The ballistic specific intensity becomes now  . In most cases shown below the absorption coefficient and the reduced scattering coefficient of the semi-infinite medium are assumed to be μa = 0.01 mm−1 and
. In most cases shown below the absorption coefficient and the reduced scattering coefficient of the semi-infinite medium are assumed to be μa = 0.01 mm−1 and  , respectively, which are typical values for biological tissue in the near-IR spectral range. If not stated otherwise we consider the Henyey-Greenstein (HG) scattering phase function4 for different values of the anisotropy factor g, where the corresponding expansion coefficients are given by fl = gl. The relative refractive index of the non-scattering medium is set to 1.0 whereas the refractive index of the scattering medium is set to n = 1.4 if not stated otherwise. In the following we refer to the developed transport solution as the modified spherical harmonics method (MSHM).
, respectively, which are typical values for biological tissue in the near-IR spectral range. If not stated otherwise we consider the Henyey-Greenstein (HG) scattering phase function4 for different values of the anisotropy factor g, where the corresponding expansion coefficients are given by fl = gl. The relative refractive index of the non-scattering medium is set to 1.0 whereas the refractive index of the scattering medium is set to n = 1.4 if not stated otherwise. In the following we refer to the developed transport solution as the modified spherical harmonics method (MSHM).
We start with the spatially-resolved reflectance in the steady-state domain which is caused by an incident unmodulated light source having two different beam radii η. Figure 1 contains the reflectance obtained from equation (18) as well as the result of the MC method. An excellent agreement is obtained for both beam radii. Thus, we also computed the relative differences between both methods in the case of the smaller beam radius and included them in the inset. Within the stochastic nature of the MC simulations an exact agreement is found.
Figure 2 displays the steady-state reflectance as function of the radial distance for a semi-infinite medium having two different absorption coefficients. For the less absorbing tissue we computed the relative differences between the MC simulation and the MSHM which are depicted in the inset. In accordance with the first comparison the MSHM leads practically to the same reflectance as the MC simulations for both absorption coefficients.
For the next comparison the absorption coefficient of the scattering half-space is significantly increased relative to the figures above. Figure 3 shows the steady-state reflectance obtained from the MC simulation (symbols), the MSHM (solid lines) and the DA (dashed lines). In that cases the DA cannot be applied for modeling adequately the back-reflected photons which is a well-known shortcoming of the diffusion theory.
The influence of the scattering phase function on the spatially resolved reflectance is considered in figure 4. To this end we use the HG phase function with g = 0.9 for the case of a highly forward scattering medium and the Rayleigh function f(ŝ · ŝ′) = 3[1 + ( ŝ · ŝ′)2]/(16π) for the case of almost isotropic scattering. Within the MSHM this function is given using the expansion coefficients fl = δl0 + 0.1δl2. The solid lines correspond to the MSHM whereas the symbols display the results of the MC simulations. In addition, the reflectance in DA29 caused by the assumed Gaussian beam is represented by the dashed line. Again, the agreement between the analytical and the numerical solution of the RTE is excellent, whereas DA performs bad especially at short distances.
We now consider the Mie phase function i.e. the solution of Maxwell's equations for the scattering of a plane wave by a sphere30. To this end we computed the expansion coefficients according to Eq. (11). In figure 5 the spatially-resolved reflectance for the Mie phase function and the Rayleigh function are shown and compared to the results obtained by the MC method (symbols). For calculation of the Mie phase function a sphere having a diameter of 1 μm and a refractive index of 1.59 is assumed to be surrounded by water with index 1.33. The wave length of the unpolarized incident plane wave is assumed to be λ = 633 nm. The refractive index of the scattering medium is set to n = 1.33.
Figure 6 displays the internal steady-state fluence according to equation (19) due to an unmodulated narrow incident Gaussian beam with radius η = 0.05 mm. The fluence is evaluated very close to the reflecting boundary at z = 0.05 mm. Similar as in the comparisons above the MSHM (solid line) coincidences excellently with the internal fluence obtained from the MC simulation (noisy curve and open circles in the inset).
In figure 7 we show a comparison between the MSHM and the MC method in the TFD. To this end we evaluated the reflectance R(ρ) = A(ρ) exp[−iϕ(ρ)] according to equation (18) for two values of the angular modulation frequency ω = 2πf which covers the typical frequencies used in diffuse optical imaging. The amplitude A(ρ) = |R(ρ)| and the phase shift ϕ(ρ) = −arg[R(ρ)] are verified with MC simulations. Here the corresponding MC results are obtained via a discrete Fourier transformation of the time-resolved reflectance caused by an infinitely short light pulse. The inset shows the phase shift for the smaller source-detector separations which exhibits an noticeable curved course due to the Gaussian intensity profile of the incident beam. It can be seen that the MSHM enables an accurate modeling of the sinusoidally modulated reflected light.
For the next comparison we evaluated equation (18) for a variety of angular modulation frequencies to reconstruct the time-resolved impulse response for the reflected light R(ρ, t) according to equation (20). Figure 8 shows the time-resolved reflectance for two different source-detector separations. Here the solid lines correspond to the MSHM, the noisy curves (and the symbols in the inset) are the result of the MC simulations and the dashed lines denote the solution of the diffusion equation under the extrapolated BC4. The radius of the lateral intensity profile is η = 0.5 mm. While the MSHM and MC simulation are in excellent agreement for both source-detector separations the DA shows significant differences compared to the transport theory solutions even for relatively large time values.
For a fixed source-detector separation of ρ = 4.05 mm we investigated the influence of the refractive index mismatch on the time-resolved reflectance. Figure 9 displays the result of the MSHM (solid lines), the MC simulation (noisy curves, symbols in the inset) and the DA (dashed lines). The radius of the lateral intensity profile is η = 0.3 mm.
Similar to the previous comparison the DA cannot be applied for accurate modeling the photon propagation for both matched and mismatched BC for early times.
Discussion
In conclusion, we have proposed a radiative transport solution for modeling the photon propagation in the three-dimensional semi-infinite medium which is an essential advance in view of the currently available solutions and approaches for solving the three-dimensional RTE. To this end the RTE was solved subject to the exact specular reflecting BC. The particular solution to the inhomogeneous RTE was obtained without recourse to the spatially-resolved impulse response by seeking a similarity solution which can be evaluated rapidly and accurately. In contrast to the classic spherical harmonics method (PN approximation) the proposed solution exhibits decisive differences and novelties. For example, the system of linear equations (12) as well as the eigenvalue problem (16) depend only on the scalar wave number q instead of the two-dimensional vector q = (q1, q2) resulting in considerable simplifications and reduced computational cost. In addition, the number of equations is reduced by a factor of 2. The derived equations were successfully verified by comparisons with MC simulations in the three commonly measurement domains showing, within the stochastic nature of the simulations, an exact agreement.
Finally, we mention that the proposed method can be extended in several ways. For example, arbitrary spatial and temporal shapes of the incident source can be considered and the solid angle for calculating the reflectance can be changed. A further important extension is that solutions for more complicated geometries such as the layered tissue structure can be obtained without alteration of the overall solution approach which will be presented in a forthcoming article.
Methods
Implementation and evaluation
The proposed solution was implemented with a non-optimized MATLAB script. The zero order Hankel transform which appears in Eqs. (18) and (19) was evaluated using the Gaussian Legendre quadrature method with 240 supporting points. The time-resolved reflectance was generated from the frequency domain Green's function via the discrete Fourier transform. The computation time needed for obtaining the results in the steady-state and the TFD was about one second whereas the time-resolved reflectance required about 30 seconds. The corresponding MC simulation time took about 20 hours for the steady-state domain and about four days in the TFD and time domains.
We additionally note that due to convenience the specific intensity of the incident beam which has entered the scattering medium was normalized to unity. This means that the specular reflection at the entry into the semi-infinite medium has not been considered. However, this effect can be easily taken into account by multiplying the final results above with the transmission coefficient T = 1 − (n − 1)2/(n + 1)2.
The ballistic contribution
In order to derive the ballistic contribution we can consider the inhomogeneous version of Eq. (4)

One possibility to solve this equation is given by performing the Fourier transform Gb(k, ŝ) = ∫ Gb(r, ŝ)e−ik·rd3r. Therefore, the spectral component for the infinite medium becomes

whose inverse is a standard transform pair which corresponds with Eq. (5). It can be seen that the infinite-space Green's function is simultaneously the wanted half-space Green's function which satisfies the specular reflection BC (3).
References
Case, K. M. & Zweifel, P. F. Linear transport theory (Addison-Wesley, New-York, 1967).
Chandrasekhar, S. Radiative transfer (Dover Publications, New-York, 1960).
Ishimaru, A. Wave propagation and scattering in random media (Academic Press, New York, 1978).
Martelli, F., Del Bianco, S., Ismaelli, A. & Zaccanti, G. Light propagation through biological tissue and other diffusive media: theory, solutions and software (SPIE Press, Bellingham, 2010).
Ntziachristos, V. Going deeper than microscopy: the optical imaging frontier in biology. Nature Methods 7, 603–614 (2010).
Backman, V. et al. Detection of Preinvasive Cancer Cells. Nature 406, 35–36 (2000).
Weissleder, R. & Ntziachristos, V. Shedding light onto live molecular targets. Nature Medicine 9, 123–128 (2003).
Wang, L. V. Multiscale photoacoustic microscopy and computed tomography. Nature Photonics 3, 503–509 (2009).
Xu, X., Liu, H. & Wang, L. V. Time-reversed ultrasonically encoded optical focusing into scattering media. Nature Photonics 5, 154–157 (2011).
Ntziachristos, V., Ripoll, J., Wang, L. V. & Weissleder, R. Looking and listening to light: the evolution of whole-body photonic imaging. Nat. Biotechnoloy 23, 313–320 (2005).
Williams, M. M. R. The three-dimensional transport equation with applications to energy deposition and reflection. J. Phys. A: Math. Gen. 15, 965–983 (1982).
Williams, M. M. R. The searchlight problem in radiative transfer with internal reflection. J. Phys. A: Math. Theor 40, 6407–6425 (2007).
Williams, M. M. R. Three-dimensional transport theory: An analytical solution of an internal beam searchlight problem-I. Annals of Nuclear Energy 36, 767–783 (2009).
Ganapol, B. D. & Kornreich, D. E. Three-dimensional transport theory: An analytical solution of an internal beam searchlight problem-II. Annals of Nuclear Energy 36, 1242–1255 (2009).
Wang, L. V., Jacques, S. L. & Zheng, L. MCML–Monte Carlo modeling of light transport in multi-layered tissues. Computer Methods and Programs in Biomedicine 47, 131–146 (1995).
Patterson, M. S., Chance, B. & Wilson, C. Time resolved reflectance and transmittance for the non-invasive measurement of tissue optical properties. Applied Optics 12, 2331–2336 (1989).
Farrell, T. J., Patterson, M. S. & Wilson, B. A diffusion theory model of spatially resolved, steady-state diffuse reflectance for the noninvasive determination of tissue optical properties in vivo. Med. Phys. 19, 879–888 (1992).
Arridge, S. R., Cope, M. & Delpy, D. T. The theoretical basis for the determination of optical pathlengths in tissue: temporal and frequency analysis. Phys. Med. Biol. 37, 1531–1560 (1992).
Liemert, A. & Kienle, A. Light diffusion in N-layered turbid media: frequency and time domains. J. Biomed. Opt. 15, 025003 (2010).
Vitkin, E. textitet al. Photon diffusion near the point-of-entry in anisotropically scattering turbid media. Nature Communications 2, 587 (2011).
Martelli, F. et al. Heuristic Greens function of the time dependent radiative transfer equation for a semi-infinite medium. Opt. Express 15, 18168–18175 (2007).
Torricelli, A. et al. Time-Resolved Reflectance at Null Source-Detector Separation: Improving Contrast and Resolution in Diffuse Optical Imaging. Phys. Rev. Lett. 95, 78101 (2005).
Pifferi, A. et al. Time-Resolved Diffuse Reflectance Using Small Source-Detector Separation and Fast Single-Photon Gating. Phys. Rev. Lett. 100, 138101 (2008).
Panasyuk, G. Y, Schotland, J. C. & Markel, V. A. Radiative transport equation in rotated reference frames. J. Phys. A: Math. Gen. 39, 115–137 (2006).
Machida, M., Panasyuk, G. Y., Schotland, J. C. & Markel, V. A. The Green's function for the radiative transport equation in the slab geometry. J. Phys. A: Math. Theor. 43, 065402 (2010).
Liemert, A. & Kienle, A. Light transport in three-dimensional semi-infinite scattering media. J. Opt. Soc. Am. A 29, 1475–1481 (2012).
Modest, M. F. Radiative heat transfer (Academic press, London, 2003).
Kienle, A. Lichtausbreitung in biologischem Gewebe dissertation (University of Ulm) (1994).
Kienle, A. & Patterson, M. S. Improved solutions of the steady-state and the time-resolved diffusion equations for reflectance from a semi-infinite turbid medium. J. Opt. Soc. Am. A 14, 246–254 (1997).
Bohren, C. F. & Huffman, D. R. Absorption and scattering of light by small particles, Wiley-Interscience, New York (1998).
Author information
Authors and Affiliations
Contributions
A.L. derived the analytical RTE solutions. A.K. developed the Monte Carlo program. Both authors wrote the article and discussed the results.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Liemert, A., Kienle, A. Exact and efficient solution of the radiative transport equation for the semi-infinite medium. Sci Rep 3, 2018 (2013). https://doi.org/10.1038/srep02018
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep02018
This article is cited by
-
A novel spatially resolved interactance spectroscopy system to estimate degree of red coloration in red-fleshed apple
Scientific Reports (2021)
-
Verification method of Monte Carlo codes for transport processes with arbitrary accuracy
Scientific Reports (2021)
-
Analytical solutions of the radiative transport equation for turbid and fluorescent layered media
Scientific Reports (2017)
-
There’s plenty of light at the bottom: statistics of photon penetration depth in random media
Scientific Reports (2016)
-
A New Route for Unburned Carbon Concentration Measurements Eliminating Mineral Content and Coal Rank Effects
Scientific Reports (2014)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.