Abstract
We present an anisotropic optical feedback technique for controlling light polarisation. The technique is based on the principle that the effective gain of a light mode is modulated by the magnitude of the anisotropic feedback. A new physical model that integrates Lamb's semi-classical theory and a model of the equivalent cavity of a Fabry-Perot interferometer is developed to reveal the physical nature of this technique. We use this technique to measure the phase retardation, optical axis, angle, thickness and refractive index with a high precision of λ/1380, 0.01°, 0.002°, 59 nm and 0.0006, respectively.
Similar content being viewed by others
Introduction
Polarisation is a very fundamental property of light and is necessary to account for the vectorial character of electromagnetic waves. Many processes in optics are determined by the polarisation states of the beams involved. Recently, research into the polarisation of light in lasers with optical feedback has attracted considerable interest1,2,3,4,5,6,7,8,9. Floch and co-workers1,2 observed the polarisation switches and a hysteresis effect by changing the intracavity anisotropy values of a laser. Stephan and co-workers3 experimentally and theoretically studied the polarisation changes induced by optical feedback from a polariser external to the cavity. However, in the prior works, the duty ratio of the two polarisation states could not be controlled; thus, the effect of the switches in polarisation could not be used for optical measurements.
We present a completely new technique for polarisation control based on anisotropic optical feedback. In this new technique, a birefringent crystal or other material with birefringent characteristics placed in a feedback cavity forms an anisotropic feedback cavity. The azimuth of the optical axis, phase retardation, thickness and refractive index of the birefringent material determined the magnitude of the anisotropy of the optical feedback cavity. The polarisation states flip from the initial polarisation direction to the orthogonal direction as the length of the feedback cavity is tuned. The position of the polarisation flip is determined by the characteristics of the birefringent materials. We measure the position of the polarisation flip to calculate the characteristic parameters.
In this study, we build an anisotropic optical feedback system to control the polarisation of light and to observe polarisation flipping. We also present a new physical model that integrates Lamb's semi-classical theory and a model of the equivalent cavity of a Fabry-Perot interferometer to analyse the dynamics of polarisation flipping. New physical phenomena are observed through this anisotropic optical feedback system.
Birefringent materials, such as optical wave plates, are widely used in optical systems related to ordinary light polarisation, such as laser heterodyne interferometers, optical filters, optical isolators and ellipsometers10,11,12. The precision of the optical wave plate determines the precision of these optical systems. To manufacture high precision wave plates, high precision methods for measuring phase retardation are needed. Some methods for phase retardation measurements have been proposed13,14,15, however, these methods have low precision for multiorder half-wave plates and a careful alignment of several polarisation components is needed. The complicated setups for such experiments and data analysis are also expensive. In this study, a polarisation control technique to achieve phase retardation measurements with a high precision of λ/1380.
Many materials exhibit strong optical birefringence, such as wave plates, biological tissues, liquid crystals and fibres. For these materials, the azimuth of the optical axis determineds the performance of the materials. For a birefringent fibre, the optical axis must be accurately aligned with a particular axis of the device to avoid polarisation cross coupling. In many biological tissues, the azimuth of optical axis directly correlates with the long-axis orientation of collagen fibres. Therefore, it is important to determine the azimuth of optical axis of birefringence materials. Some methods have been proposed to measure the azimuth of optical axis. Polarisation sensitive optical coherence tomography (PS-OCT) is a noninvasive imaging technique used to determine the birefringence of materials and the azimuth of the optical axis16,17,18. Of the methods for optical axis determination listed above, some require expensive instrumentation and the others cannot meet the high requirements in measurement accuracy and resolution required for industrial and scientific use. In this study, we use a polarisation control technique to measure the optical axis with a precision of 0.01°.
Angle measurements are important in many applications, such as the control of adaptive optical systems, the automation of manufacturing, robotics and coordinate-measuring instruments. Autocollimators19,20 and interferometers21,22 are traditionally employed to measure angles. Although these two methods provide high precision, devices based on these methods are usually large, thus, in many cases, the devices are difficult to integrate with machines for online measurements in many cases. In this study, we use the polarisation control technique to achieve angle measurement with a precision of 0.002°.
The thickness and refractive index are fundamental parameters of optical materials. Some methods for measuring the thickness and refractive index, such as the minimum deviation method, total internal reflection method and interferometeric methods, have been proposed and applied in industry areas. However, one problem, common to all of these methods, is that the thickness and refractive index cannot be measured simultaneously. In this study, we use a polarisation control technique to measure the thickness and refractive index simultaneously with a precision of 59 nm and 0.0006.
Results
Polarisation control system
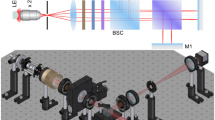
The experimental setup employed in this work is shown in Figure 1a. The setup consists of four parts: a light source, a feedback cavity, a detecting part and a signal acquisition system.
Experimental setup for polarisation control and measurement curves.
(a) Experimental setup. D1, D2, photo detectors; M1, M2, high reflectors; M3, window film; S, birefringent sample; ME, feedback mirror; PZT, piezoelectric transducer; P, polariser; DA, digital–to–analogue signal converter; AD, analogue–to–digital signal converter; AMP, voltage amplifier. (b) Measured curves.
The extraordinary light source is a He-Ne gas laser with a wavelength of 632.8 nm. The resonator is composed of mirrors M1 and M2 with reflectivities of 99.8 and 98.8%, respectively and a window film M3. The resonator is half-intracavity, with a length of 150 mm. The laser mode is single mode, linearly polarised and initially polarised in the x direction, as shown in Figure 1a. The ratios of gaseous pressures in the resonator are He:Ne = 9:1 and Ne20:Ne22 = 1:1.
The feedback cavity is formed by M2 and the the feedback mirror ME, with the birefringent sample S between the mirrors. The length of the feedback cavity is 100 mm. ME has a reflectivity of 10% and is used to reflect laser beams back into the resonator. A piezoelectric transducer (PZT) ,which is driven by a triangular voltage wave is used to tune, push and pull ME. The birefringent sample S is made up of quartz material and the optical axis orientation is parallel to the sample surface. The surface roughness and parallelism of the wave plate are less than 1 nm and 5, respectively.
The detection system is formed by the polariser P, detector D2 and oscilloscope 2. Polariser P is used to separate the different polarisation states of the laser. In our experiment, the polarisation direction of the polariser is orthogonal to the initial direction of the laser polarisation, as shown in Figure 1a. When the direction of the laser polarisation is the same as that of the polarisation direction of the polariser, the beam can reach and be detected by detector D2. Otherwise, the output voltage of D2 remains at the minimum voltage. Thus, changes in the output voltage for detector D2 indicate polarisation flipping for the laser.
The signal acquisition system consists of detector D1 and oscilloscope 1. D1 is used to measure the laser intensity.
Polarisation flipping curve
For the case in which the length of the feedback cavity is tuned with the PZT, the experimental results for polarisation flipping and intensity transfer are shown in Figure 1b.
In Figure 1b, the top curve shows the output from D1 for the laser intensity. The curve differs from that for conventional laser feedback phenomena. Firstly, minima at the B and F points occur whereas the conventional laser feedback curves are similar to a cosine shape23. Second, the polarisation state flips 90° vertically at positions B and F. The distance between positions A and D or E and H is one period of λ/2. The position, B or F, of the polarisation flip is determined by the phase retardation magnitude of the sample S.
The middle curve in Figure 1b shows the voltage output from D2. Initially, when the PZT is not scanned, we change the polarisation direction of the polariser P so that the direction is orthogonal to the initial polarisation state of the laser and the laser cannot pass through the polariser. Then, the minimum voltage is observed on oscilloscope 2. When the PZT is scanned, the polarisation flipping occurs, as shown in Figure 1b. The polarisation states changes between the x and y directions. Thus, a square wave is observed on oscilloscope 2. Each transition indicates a single polarisation flip.
The lowest curve in Figure 1b is the driving voltage applied to the PZT. The voltage is a triangular wave with a maximum of 100 V. At this voltage, the maximum displacement of the PZT is 0.5 μm.
The relation between the position of the flip and the magnitude of the phase retardation is shown in Figure 2a.
Phase retardation measurement
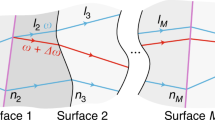
In the feedback cavity, light passes through the birefringent sample S twice, so the retardation of ordinary light and extraordinary light in Figure 2a is 2δ, where δ is the phase retardation of the birefringent material S. Based on Figure 2a, the relation between the position of the polarisation flip and the phase retardation can be expressed by:

where C is the point with intensity equal to that point B and G is the equivalent of F. lBC is the difference in the length of the feedback cavity between points C and B and lAD, lFG and lEH are defined similarly. VBC is the PZT voltage between points C and B and VAD, VFG and VEH are defined similarly.
According to the relation given in Eq. (1), the phase retardation of the birefringent material or wave plate can be measured with high precision. The measurement results are shown in Figure 2b. The results indicate that the reproducibility of the phase retardation measurement is better than λ/1380, as shown in Figure 2b.
Optical axis determination
If the sample S is rotated perpendicular to the direction of laser propagation to change the angle between the optical axis and the direction of the laser polarisation, the curves for the polarisation flips differ, as shown in Figure 3. If the optical axis is close to the x-axis, the gradient of the polarisation state decreases. The gradient becomes zero when the optical axis is parallel to the x-axis. This result can be used to determine the azimuth of the optical axis. The gradient of the intensity of the polarisation states is highly sensitive to the relative positions of the optical axis and the initial polarisation direction of the laser. The resolution of the azimuth of the optical axis is better than 0.01°.
Angle measurement
If the sample S in the feedback cavity is rotated, the phase retardation of the birefringent material is changed due to interference effects at the surface of S (Fig. 4a). The relation between the angle θ and the phase retardation δ is given by

where rob-a and reb-a are the reflectivities from the wave plate to air of ordinary light and extraordinary light, respectively; toa-b and tea-b are the transmittances from air to the wave plate of the ordinary light and extraordinary light, respectively; and tob-a and teb-a are the transmittances of from the wave plate to air of the ordinary light and the extraordinary light, respectively. Eoo and Eee are the electric field vectors of the ordinary and extraordinary light, respectively, through the wave plate; E′oo and E′ee are the amplitudes of the ordinary and extraordinary light, respectively; and ϕo and ϕe are the phases of the ordinary light and extraordinary light, respectively. Eo and Ee are the initial electric field vectors of the ordinary and extraordinary incident light, respectively; and k = 2π/λ. noo and nee represent the refractive indices of the ordinary light and extraordinary light, respectively, at a rotation angle of θ. no and ne are the refractive indices of the ordinary light and extraordinary light, respectively, when the rotation angle is zero.
Therefore, the variation in the phase retardation reflects the angle of rotation of the birefringent sample S. The relation between the phase retardation and the angle of rotation of sample S, as given by Eq. (2), can be used to measure the angle variation. The experimental curve of the variation of the phase retardation with angle is shown in Figure 4b. The advantages of this method for angle measurement are: low cost, effective power, compact, flexible, fast response and high precision.
The angular resolution of this laser feedback method can be estimated by Eq. (3). Where R is the angular resolution of laser feedback instrument; the 0.1° is about the repeatability of phase retardation measurement of laser feedback instrument; the angular magnitude of 0.2° is the half-cycle of phase retardation variation; the phase retardation magintude of 10° is the amplitude of phase retardation variation.

According to Eq.(3), the angular resolution is 0.002° in the range of ±15°.
Thickness and refractive index measurement
To simultaneously measure the thickness and refractive index, we eliminate the interference effect at the surface of the sample S with a refractive index matching liquid or an antireflection coating. We choose a quartz wave plate as the birefringent material and rotate the plate around the slow axis to determine the relations among the phase retardation, rotation angle, thickness and refractive index. Through a simple derivation, the relation can be expressed as

where d is the thickness of the quartz wave plate, no and ne are the refractive indices of ordinary light and extraordinary light at a wavelength ofλ and N is the order of the wave plate.
In Eq. (4), there are four unknowns. If the sample S is rotated four times or more times, there will be four or more equations to solve for the unknown variables, as given by Eq. (5):

Experimentally, a series of phase retardations is measured as the wave plate is rotated. The measurement data are listed in Table 1. The angle is measured with an autocollimators.
We fit the data in Table 1 to Eq. (4). The numerical solutions for the unknown variations are listed in Table 2. The actual values for the thickness and refractive indices are measured by interferometry and the deviation method, respectively. The measurement precision are 10 nm and 10−6, respectively. The measured values are given as the results calculated from the experimental data. The results show that the maximum error of the thickness is 59 nm; this error shows reasonable agreement between the measured values and the actual thickness of the quartz wave plate, as measured by interferometry. The maximum error of the refractive indices for ordinary light and extraordinary light is 0.0006.
Discussion
When the length of the feedback cavity is scanned with the PZT, the effective gains of the ordinary light and extraordinary light are modulated. We integrate a model of using the equivalent cavity of a Fabry-Perot interferometer and Lamb's semi-classical theory to analyse the variation in the effective gains.
The model for the equivalent cavity of a Fabry-Perot interferometer is given by24

where Roeff and Reeff are the equivalent mirror reflectivities for ordinary light and extraordinary light, R2 is the reflectivity of the high reflector M2, r2 and t2 are reflection and transmission coefficients of the high reflector M2, re is the reflection coefficient of mirror ME, k = 2π/λ is the wave number, λ is the wavelength of the laser and δ is the phase retardation of the birefringent material.
According to Lamb's semi-classical theory, the effective gain is given by25

where α′o and α′e are the effective gains for ordinary light and extraordinary light, αo and αe are the net gains for ordinary light and extraordinary light, θoe and θeo are the mode competition coefficients, βo and βe are the self-saturation coefficients.
Based on Eq. (6), a polarisation flip occurs under conditions of αo > 0, αe > 0, α′o > 0, α′e < 0 or αo > 0, αe > 0, α′o < 0, α′e > 0. The expressions for the effective gain will be calculated in the next section.
In Eq. (6), the net gain α can be expressed by

where Zi is the plasma dispersion function, η is the degree of relative excitation degree, which is approximately 1.33 and ξ is the frequency parameter. Zi, ξ and F are expressed by26

where νo and νe are the frequencies of the ordinary light and extraordinary light, ν0 is the centre frequency of the laser and Δ is the longitudinal mode spacing, which is approximatelly 833 MHz.
The self-saturation coefficients are given by

where γa = 24 MHz, γb = 83 MHz and Hr is the real part of the complex function H. The other parameters are given by

where γ = 210 MHz, Ja is the angular momentum quantum number, m is a constant and  = 1. The competition coefficients θ for the modes are given by
= 1. The competition coefficients θ for the modes are given by

Based on Eqs (5)–(11), we can obtain the effective gain of the laser for different feedback cavity lengths. At some lengthes, the effective gain of the ordinary light is greater than 0 and at other lengths, the effective gain of the extraordinary light is greater than 0, as shown in Figure 5. However, the effective gains for ordinary and extraordinary light cannot be greater than 0 for the same feedback cavity under our experimental conditions. According to Lamb's semi-classical theory, the laser mode flips when the effective gain is greater than 0. Therefore, the polarisation state flip and laser intensity transfer occur when the length of the feedback cavity is tuned with the PZT. The experimental results for the polarisation flipping and intensity transfer are shown in Fig. 1b.
In conclusion, we have demonstrated an anisotropic feedback system for polarisation control. A new physical model was constructed to analyse the polarisation flipping induced by anisotropic optical feedback. We have lready achieved a high precision of λ/1380 in phase retardation measurements. We also applied the polarisation control system to measure the optical axis, angle, thickness and refractive index with precisions of 0.01°, 0.002°, 59 nm and 0.0006, respectively.
Methods
Feedback mirror driven by a PZT
We used a PZT from Physik Instrumente Inc. (PI, Germany) as a driver to push and pull the feedback mirror as a triangular voltage wave was applied to the PZT. The PZT parameters are listed in Table 3.
Data acquisition and analysis
The datas were acquired with an acquisition card from National Instruments Inc. (NI, USA). The Labwindows/CVI program developed by NI was used to analyse the data.
Materials
Quartz material was used in the experiments.
References
Floch, A. L., Ropars, J. M. & Lenornamd, G. Dynamics of laser eigenstates. Phys. Rev. Lett. 52, 918–921 (1984).
Ropars, G., Floch, A. L. & Naour, R. L. Polarization control mechanisms in vectorial bistable lasers for one-frequency systems. Phys. Rev. A. 46, 623–640 (1992).
Stephan, G. & Hugon, D. Light polarization of a quasi-isotropic laser with optical feedback. Phys. Rev. Lett. 55, 703–706 (1985).
Panajotov, K. et al. Polarization switching induced by phase change in extremely short external cavity vertical-cavity surface-emitting lasers. Appl. Phys. Lett. 84, 2763–2765 (2004).
Jiang, S. et al. High-frequency polarization in vertica-cavity surface-emitting lasers. Appl. Phys. Lett. 63, 3545–3547 (1993).
Li, H. et al. Stable polarization self-modulation in vertica-cavity surface-emitting laser. Appl. Phys. Lett. 72, 2355–2357 (1998).
Chen, Y. C. & Liu, J. M. Temperature-dependent polarization behavior of semiconductor lasers. Appl. Phys. Lett. 45, 731–733 (1984).
Agrawal, G. P. Effect of fiber-far end reflections on intensity and phase noise in GaAsp semiconductor laser. Appl. Phys. Lett. 45, 957–959 (1984).
Seo, D. S. et al. Compound cavity modes in semiconductor lasers with asymmetric optical feedback. Appl. Phys. Lett. 54, 990–992 (1989).
Rothen, A. The ellipsometer, an apparatus to measure thickness of thin surface films. Rev. Sci. Instrum. 16, 26–30 (1945).
Rothen, A. & Hanson, M. Optical measurements of surface films. I. Rev. Sci. Instrum. 19, 839–841 (1948).
Rothen, A. Improve method to measure the thickness of thin films with a photoelectric ellipsometer. Rev. Sci. Instrum. 28, 283–285 (1957).
Yao, L., Zhiyao, Z. & Runwen, W. Optical heterodyne measurement of the phase retardation of a quarter-wave plate. Opt. Lett 13, 553–555 (1988).
Wang, B. & Hallamn, W. Accuracy assessment of a linear birefringence measurement system using a Soleil–Babinet compensator. Rev. Sci. Instrum. 70, 4066–4070 (2001).
Cattaneo, S., Zehnder, O., Gunter, P. & Kauranen, M. Nonlinear optical technique for precise retardation measurements. Phys. Rev. Lett. 88, 243901–243903 (2002).
De Boer et al. Two-dimensional birefringence imaging in biological tissue by polarization-sensitive optical coherence tomography. Opt. Lett. 22, 934–946 (1997).
De Boer et al. Imaging thermally damaged tissue by polarization sensitive optical coherence tomography. Opt. Express. 3, 212– (1998).
De Boer, J. F., Milner, T. E. & Nelson, J. S. Determination of the depth-resolved Stokes parameters of light backscattered from turbid media by use of polarization-sensitive optical coherence tomography. Opt. Lett. 24, 300– (1999).
Luther, G. G. & Deslattes, R. D. Single axis photoelectronic autocollimator. Rev. Sci. Instrum. 55, 747–750 (1984).
Schuda, F. J. High-precision, wide-range, dual-axis, angle monitoring system. Rev. Sci. Instrum. 54, 1648–1652 (1983).
Hussain, G. & Ikram, M. Optical measurements of angle and axis of rotation. Opt. Lett. 33, 2419–2421 (2008).
Shi, P. & Stijins, E. Improving of the linearity of the Michelson interferometric angular measurement by a parameter compensation method. Appl. Opt. 32, 44–51 (1993).
King, P. G. & Steward, G. J. Metrology with an optical maser. New Sci. 17, 180–180 (1963).
Groot, P. J. Ranging and velocimetry signal generation in a backscatter modulated laser diode. Appl. Opt. 27, 4475–4480 (1988).
Lamb, E. Theory of an optical maser. Physics Review. 134, A1429–A1450 (1964).
Dovle, W. M. & White, M. B. Effects of Atomic Degeneracy and Cavity Anisotropy on the Behavior of a Gas Laser. Physical Review. 147, 359–367 (1966).
Acknowledgements
This work was supported by the Key Program of the National Natural Science Foundation of China (NSFC) (No. 61036016) and the Scientific and Technological Achievements Transformation Project of the Beijing Municipal Education Commission.
Author information
Authors and Affiliations
Contributions
W.C. designed the experiments, developed the concept, constructed up the optical hardware and wrote the software to control the system and data acquisition. S.Z. designed the experiments, developed the concept and supervised the entire project. X.L. contributed to the design of the system and considerably improved the presentation of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Chen, W., Zhang, S. & Long, X. Polarisation control through an optical feedback technique and its application in precise measurements. Sci Rep 3, 1992 (2013). https://doi.org/10.1038/srep01992
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01992
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.