Abstract
Recent experimental advances have measured individual coin components in discrete time quantum walks, which have not received the due attention in most theoretical studies on the theme. Here is presented a detailed investigation of the properties of M, the difference between square modulus of coin states of discrete quantum walks on a linear chain. Local expectation values are obtained in terms of real and imaginary parts of the Fourier transformed wave function. A simple expression is found for the average difference between coin states in terms of an angle θ gauging the coin operator and its initial state. These results are corroborated by numerical integration of dynamical equations in real space. The local dependence is characterized both by large and short period modulations. The richness of revealed patterns suggests that the amount of information stored and retrieved from quantum walks is significantly enhanced if M is taken into account.
Similar content being viewed by others
Introduction
Since the seminal work on quantum walks (QW) by Aharonov et al.1, different versions and applications of the original proposal have been investigated2,3,4,5. The ultimate goal is to determine the probability ρ of finding the moving particle, hence the amplitude of wave function, as function of position and time. In the discrete time quantum walk formulation (DTQW)1, the dynamics is dictated both by the usual Hamiltonian operator and by a unitary operator acting on so-called coin variables. They influence, in different ways, the jumping probability from the particle's current place to any of the lattice sites. In such cases, ρ is obtained by summing up the square modules of the different wave function components associated to the coin states.
In contrast, very little attention has been paid until now to the dynamics of the individual coin components6,7, both from theoretical8,9 and experimental10,11,12,13,14 points of view. Indeed, only very recently experimental measurements7 were able to identify and separate the two coin state contributions to ρ. In this particular case, the influence of coin operator is reflected in the photon polarization. In the other exhaustively investigated electron system, the coin operator acts on the spin variable. The identification of coin state components opens new perspectives for a fine control of quantum walks. However, Ref. 7 does not provide a deeper analysis of each state contribution. This is the main motivation for this work, in which we explore in detail several features of the difference between square modulus of coins states. For the sake of brevity, it will be denoted by M, much inspired by the notation for magnetization of spin systems. Thus, we consider ρ and M as independently measurable physical properties of the moving particle.
The general framework we propose allows for the identification of global and local properties. They are interpreted, respectively, as the corresponding average properties associated to the coin states (polarization or spin component), or as expression of complex (e.g. periodic, modulated, commensurate or incommensurate) microscopic patterns. For the sake of definitiveness, we consider the simple one dimensional chain (with open or closed boundary conditions) with two coin states and investigate the properties of the differences between the square modules of the two components. We were able to derive exact analytical results for the global properties, while numerical integration of the wave function complements our results for local properties for distinct initial conditions. Of course the presented framework can be extended to higher dimension geometries and/or to a larger number of coin states.
We think that, by a detailed characterization of M, other properties of DTQW can be explored. The results we discuss herein are obtained for a field free condition and, despite the fact that the output of DTQW dynamics may look random, it is essentially deterministic. If we consider the action of external fields, it is possible to connect DTQW to other recently discovered properties of nano-devices, which have been unified into the so-called spintronics15 framework.
In such nano-structures, the mean free path between successive collisions of charge carriers becomes larger than the typical dimension of the devised structure. This way, they reach their destination before undergoing collisions, thus preserving its spin, which can be measured and controlled by proper external magnetic fields. For instance, in a pure charge current one has access only to Ic = I↑ + I↓ ≠ 0 but, in a spin-polarized current, it is possible to independently measure Ic = I↑ + I↓ ≠ 0 and Is = I↑ − I↓ ≠ 0, where ↑↓ indicates spin components in the up and down directions. Ic and Is are related, respectively, to the quantities ρ and M we investigate in this work. Although we restrict ourselves to field free conditions, it is possible to adequately enrich the model by adding external electric and magnetic fields, in such a way that it is possible to have situations in which Ic ≠ 0 but Is = 0, as well as Ic = 0 but Is ≠ 0. In this last extreme condition, the spin current is characterized only by its magnetic properties, as it carries no net electric charge.
Similar field combinations leading to the observed spin-Hall effect (SHE) and the inverse spin-Hall effect (ISHE)16,17,18,19 might be explored within DTQW with the inclusion of the proper fields. In the first case, which is observed in metals with strong spin-orbit interaction, carriers with opposite spins in Ic are deflected to opposite sides of the film by creating a spin current. In the inverse situation, up (or down) spin carriers are deflected according to their charge and magnetic field direction. This way, spin and charge currents are induced by the original charge and spin currents in the device.
We consider a spin 1/2 particle in a linear chain where it can occupy any available site. A discrete time evolution operator Ŵ can be defined in a Hilbert space  , where
, where  and
and  are the subspaces in which the time dependence of the chain position and spin components are embedded. Ŵ acts on the state vector
are the subspaces in which the time dependence of the chain position and spin components are embedded. Ŵ acts on the state vector  , with position |Φ〉 and spin |σ〉 components. The discrete position and time variables are indicated, respectively, by x and nτ → n.
, with position |Φ〉 and spin |σ〉 components. The discrete position and time variables are indicated, respectively, by x and nτ → n.
Within a given time step n, two successive operations are carried out by the operator Ŵ: i) the coin operator Ĉ acts on the spin component; ii) the shift operator Ŝ updates the wave function magnitude at each chain sites taking into account the new spin state. These actions are formally indicated by the expression

We decompose the spin component |σ〉 in terms of the |0〉 and |1〉 eigenvectors of Pauli matrix, i.e., |σ〉 = αR|0〉 + αL|1〉. The spin eigenstate magnitudes αR and αL are related to the jump (or shift) dynamics. Thus, the coin operator Ĉ is expressed by a unitary matrix

which is a generalization (for 0 ≤ θ ≤ π/2)) of the usual Hadamard operator Ĥ obtained by taking θ = π/4. If we start with a nearest neighbor tight-binding Hamiltonian with unitary hopping probability

the Ŝ operator is expressed by

Finally, from Eqs. (1)–(4), a single expression for Ŵ can be written, which describes the evolution of the state vector |Ψ(x, n)〉.
Results
Analytic properties
For convenience, we describe the wave function representation of |Ψ(x, n)〉 using two component vector amplitudes in order to separate the spin particle states according to the framework reported in Ref. 8. Thus,

where ψR(x, n) and ψL(x, n) are amplitudes at time n and lattice position x of a walker with, respectively, upper and lower internal degree of freedom. From Eqs. (1)–(4) the evolution of the wave function is given by transformation

Introducing the Fourier transform

the wave function evolution obeys the following simple form  , where
, where

Thus, as a function of the initial state (n = 0), the wave function at time n is  . In the sequence, using a standard approach8, we diagonalize
. In the sequence, using a standard approach8, we diagonalize  and after a tedious but straightforward calculation, the wave function components in Fourier space at time n:
and after a tedious but straightforward calculation, the wave function components in Fourier space at time n:


In Eqs. (9) and (10), sin ωk = cos θ sin k. We assume that the initial condition (n = 0) is such that the particle is at position x = 0 and the coin is in the state σ(η) = cos η|0〉 + i sin η|1〉. Using the inverse Fourier transform, we can obtain the real space wave function that leads to the probability density ρ(x, n) of observing a particle at time n and position x and to the value of M(x, n) defined by:


Asymptotic properties of the ψR(x, n) and ψL(x, n) wave functions in the large time limit have been analyzed8,9 by decomposing ρ = ρslow + ρfast. Essentially, ρslow corresponds to the non-oscillating term and ρfast to the remaining oscillating one. The contribution of the fast component is of lower order in n than that from the slow one and, for the large time limit, we can write ρ ~ ρslow. For instance, when the initial condition is η = 0,  takes the form8
takes the form8

where kα is the solution of dωk/dk + α = 0 and α = x/n. Using similar steps, it is possible to show that M(α, n) ~ Mslow(α, n), so that we obtain asymptotically the expression Mslow = −αρslow. The corresponding global values is calculated by integrating the local expression for Mslow over the position variable

which is valid for all values of η.
Numerical consequences
Numerical values of the state vector Ψ(x,n) have been obtained for a large number of initial conditions η, different choices of coin operator angle θ and system size 2L + 1. For the sake of definitiveness, we always consider x ∈ [−L,L]. The asymptotic magnetization depends on the values of both η and θ, as illustrated by the curves  and
and  in Fig. 1. It is possible to see that the numerical values corroborate the analytical expressions given above. For arbitrary initial combinations of up and down components, the typical patterns change continuously from one of the extreme cases to the other. The extreme values of
in Fig. 1. It is possible to see that the numerical values corroborate the analytical expressions given above. For arbitrary initial combinations of up and down components, the typical patterns change continuously from one of the extreme cases to the other. The extreme values of  , which depend on the initial conditions, lie in the interval
, which depend on the initial conditions, lie in the interval  . In Fig. 1b we illustrate the dependence of
. In Fig. 1b we illustrate the dependence of  . It is amazing to see that, by an adequate choice of the coin operator (through the selected value of θ), it is possible to obtain asymptotic states running from zero to unitary average magnetization per particle.
. It is amazing to see that, by an adequate choice of the coin operator (through the selected value of θ), it is possible to obtain asymptotic states running from zero to unitary average magnetization per particle.
The numerical integration allows for identifying several distinct patterns of local magnetization. Since we consider finite systems, the investigation of open boundary conditions is limited to time interval in which the probability of occupation of the x = ±L sites is negligible. From that time on, circular geometry condition becomes effective, i.e., ψ(L + 1) = ψ(−L).
Typical symmetric and antisymmetric patterns for L = 50 are shown in Fig. 2 for the θ = η = π/4 (a) and η = 0, θ = π/8 (b). In both cases, open boundary conditions persist until  , when clear non-zero values of M(±L,n) are obtained. In the first case, we observe a first rhombic structure characterized by antisymmetric rhombuses with respect to the center of the chain (x = 0). It is characterized by the dominant presence of positive and negative values of M(x,n) for x ∈ (0,L) and x ∈ (−L, 0), respectively. The circular geometry conditions becomes effective producing interference patterns that start at the boundary x = ±L and evolve towards the center of the chain. In this process, we note an inversion of the magnetization, with predominance of positive (negative) values of M at the left (right) side of the chain. The resulting patten is a tile of superposed antisymmetric rhombic units, with the wide parts being successively placed at x = 0 and x = 50 ≡ −50. For the antisymmetric initial condition, rhombuses are displaced with respect to the center of the chain, giving rising to superposed diagonal stripes going from left to right (positive M) and from right to left (negative M).
, when clear non-zero values of M(±L,n) are obtained. In the first case, we observe a first rhombic structure characterized by antisymmetric rhombuses with respect to the center of the chain (x = 0). It is characterized by the dominant presence of positive and negative values of M(x,n) for x ∈ (0,L) and x ∈ (−L, 0), respectively. The circular geometry conditions becomes effective producing interference patterns that start at the boundary x = ±L and evolve towards the center of the chain. In this process, we note an inversion of the magnetization, with predominance of positive (negative) values of M at the left (right) side of the chain. The resulting patten is a tile of superposed antisymmetric rhombic units, with the wide parts being successively placed at x = 0 and x = 50 ≡ −50. For the antisymmetric initial condition, rhombuses are displaced with respect to the center of the chain, giving rising to superposed diagonal stripes going from left to right (positive M) and from right to left (negative M).
Local values of M(x, n) and of the global probability density ρ(x, n) for two distinct choices of initial conditions for wave function and coin state when x ∈ [−50, 50].
For M, blue, white and red indicate the ranges 1 ≤ M ≤ 0.001, 0.001 ≤ M ≤ −0.0001, −0.001 ≤ M ≤ −1. For ρ, colors change smoothly from blue to red as ρ increases. Free propagation with local interference occurs until n = 50. Periodic boundary conditions give rise to rhombic patterns. In (a), M shows periodicity in time direction. In (b), interference pattern has smaller coherence. Panels (c) and (d) show the dependence of ρ for the same initial conditions as (a) and (b), respectively.
Plots for ρ like those shown in Fig. 2 are obtained, with the major difference being related to the fact that 0 ≤ ρ ≤ 1. As in the space-temporal patterns for ρ reported in Ref. 8, the observed presence of positive and negative values of M is absent in the corresponding plots for ρ. Similar plots are typical for larger values of L, provided the time axis becomes also scaled by the same factor. The values of M(x, n) for n = 28 correspond to the difference between experimental points (or blue and red bars) of Fig. 1 of Ref. 7.
To obtain a more precise insight on the possible presence of periodic magnetization we evaluate  , which measures how close two local magnetization patterns are for different instants of time n and m. The results are displayed in Fig. 3 (a) and (b), for the same conditions used to draw Fig. 2. Fig. 3a uncovers the presence of both short period correlated pattern for small values of both n and m, when Δm(i,j) reach largest absolute values. Next, the results indicate the persistence of the overall modulation pattern of the local magnetization, with period ~ 140 alternating between correlated and anti-correlated patches. They are, however, subject to a fading process that amounts to a decrease in the magnitude and a smoothing process leading to less sharp boundaries between the local values. Fig. 3b shows a different pattern, with a shorter period. It is also possible to note the disappearance of clear square tile that characterizes Fig. 3, which is replaced by diagonal stripes with decreasing correlation. Evidence of long period anti-correlated patches, as in (a), disappears being replaced by a mixture of short and large period of a stronger correlated local magnetization.
, which measures how close two local magnetization patterns are for different instants of time n and m. The results are displayed in Fig. 3 (a) and (b), for the same conditions used to draw Fig. 2. Fig. 3a uncovers the presence of both short period correlated pattern for small values of both n and m, when Δm(i,j) reach largest absolute values. Next, the results indicate the persistence of the overall modulation pattern of the local magnetization, with period ~ 140 alternating between correlated and anti-correlated patches. They are, however, subject to a fading process that amounts to a decrease in the magnitude and a smoothing process leading to less sharp boundaries between the local values. Fig. 3b shows a different pattern, with a shorter period. It is also possible to note the disappearance of clear square tile that characterizes Fig. 3, which is replaced by diagonal stripes with decreasing correlation. Evidence of long period anti-correlated patches, as in (a), disappears being replaced by a mixture of short and large period of a stronger correlated local magnetization.
Color code plots indicating the dependence of Δm(i,j) (panels (a) and (b)) and Δρ(i,j) (panels (c) and (d)) with respect to two instants of time.
In (a), a large period modulation is observed by the presence of square tile for values of n or m. Inside each square, high frequency modulation patterns are indicated by alternating green and yellow tiles. In (b), long range modulation almost vanishes, being replaced by short period correlation along the diagonal separated by cyan stripes. Results for Δρ(i,j) produce basic features (square tiles or diagonal stripes), but details have been blurred in comparison to those in Δm(i,j).
Plots for ρ are shown in Fig. 3c and 3d. For the two cases defined by the same initial conditions as in panels (a) and (b), the resulting patterns for  fade out in comparison to those shown in Fig. 3. The general structure related to short and long periods is well reproduced, but the measure Δm is much richer in details than that for Δρ.
fade out in comparison to those shown in Fig. 3. The general structure related to short and long periods is well reproduced, but the measure Δm is much richer in details than that for Δρ.
Let us now consider the time evolution of M(x, n) for fixed values of x. Typical patterns are illustrated in Fig. 4 for L = 500 and five different values x = jL/5, j = 1, 2, 3, 4, 5. They can be brought in contact with the rhombic pattern in Fig. 2. Once a site enters the region of non-zero magnetization, M(x, n) has large amplitudes corresponding to the darker border regions. The amplitudes decay as n increases, until the site enters a new rhombic region, where M becomes negative. At this moment, the amplitude suffers a sudden increase that is followed by a decaying phase. This is a periodic behavior that will be repeated for any value of x. The regions where M remains positive or negative depend on x. So, for j = 1, 2, regions of positive M are larger than those with negative M, situation that is inverted for j = 3 and 4. j = 5 corresponds to a site at the boundary x = L. In this case, there is no separation between regions of positive and negative values of M. Positive and negative values coexist in any time window. The sudden increase in the magnitude of M persists until the moment where the site L leaves one of the rhombs and enters the next one. The symmetric condition η = π/4 causes M(x = 0,n) to vanish identically for all values of n.
In order to stress differences between the two independent measures ρ and M, it is convenient to consider Fourier decompositions in the frequency space,  and
and  , as shown in Fig. 5. There ω has been normalized to the interval [−0.5,0.5]. Since the two independently defined measures are orthogonal, the Fourier decomposition clearly evidence differences in the parity of the considered signal. Of course both of them depend on the position x. For any value of x,
, as shown in Fig. 5. There ω has been normalized to the interval [−0.5,0.5]. Since the two independently defined measures are orthogonal, the Fourier decomposition clearly evidence differences in the parity of the considered signal. Of course both of them depend on the position x. For any value of x,  is dominated by a peak at ω = 0, while the band extremes at ω = ±0.5 depend on x. They decrease monotonically as j goes from 1 to 5. At j = 5 the band edge peak vanishes identically. The spectrum also present two further vanishing points at ω = ±0.25, for any value of x. The transform of the magnetization
is dominated by a peak at ω = 0, while the band extremes at ω = ±0.5 depend on x. They decrease monotonically as j goes from 1 to 5. At j = 5 the band edge peak vanishes identically. The spectrum also present two further vanishing points at ω = ±0.25, for any value of x. The transform of the magnetization  is dominated by the peaks at ω = ±0.5, while the peak at ω = 0 depends on x. In the limit x → L, the central peak vanishes identically.
is dominated by the peaks at ω = ±0.5, while the peak at ω = 0 depends on x. In the limit x → L, the central peak vanishes identically.
Amplitude of the Fourier transform  and
and  for x = 10, 250 and 500.
for x = 10, 250 and 500.
Signals are restricted to ω ∈ [0,0.5]. Common features are the broad composition of the signal and the zero amplitude at ω = 0.25. Dominant peaks at the center or at edge of the band depend both on the parity of the signal (ρ or M) and on the value of x.
Discussion
The standard DTQW on a chain with N sites has 2N degrees of freedom, but the traditional way of looking at the system output neglects half of available information. Through the analysis of M, the difference between the squared amplitudes of the wave function associated to each of the coin states, it is possible to access the sofar neglected information. The first immediate output of this analysis is that the presence of non-zero values of M indicates a preponderant contribution of one of the coin states in the value of ρ. Having a physical meaning similar to that of actual magnetization in magnetic systems, it provides a measure of the ordering of coin states as a function of space and time. The experimental access to the individual coin state components has recently been achieved by an optical system where photons play the role of walkers. Our results explore in detail several properties of M. Besides being orthogonal to the information displayed by ρ, the results for M offer a brighter contrast. This increases the possibility of designing DTQW devices for specific information storage and manipulation. By a simple algebraic combination of ρ and M it becomes possible to single out the dynamical behavior of each coin state. With the adopted formalism, it becomes possible to treat richer conditions where the presence of external fields, acting in different ways on individual coin states, may produce targeted effects similar to those treated nowadays in spintronics. Other important aspect is related to the influence that the combination of there two measures may have in connection to quantum entanglement problems. Nevertheless, further work is required to devise feasible protocols to explore these ideas.
As a final comment, we could not devise if the proposed method developed here can be extended to the continuous time quantum walk (CTQW)2,20,21 formulation of the problem. In such case, the algebraic structure of the pertinent quantum walk is related to that of the continuous time (classical) random walk (CTRW), both of which can be described with the help of an imaginary (CTQW) or real (CTRW) exponential evolution matrix22.
Methods
The analytical results have been obtained by the usual manipulation methods of dynamical equations, which includes Fourier transforming, averaging, matrix algebra and sum rules.
The numerical results are obtained from the successive evaluation of the time dependent wave function  . The discrete
. The discrete  evolution operator is obtained from Eqs. (1)–(4). Since the output if purely deterministic, no use of pseudo-random number generator is required. Time and space numerical averages are performed whenever required. All results were obtained by FORTRAN codes generated by the authors.
evolution operator is obtained from Eqs. (1)–(4). Since the output if purely deterministic, no use of pseudo-random number generator is required. Time and space numerical averages are performed whenever required. All results were obtained by FORTRAN codes generated by the authors.
References
Aharonov, Y., Davidovich, L. & Zagury, N. Quantum random walks. Phys. Rev. A 48, 1687–1690 (1993).
Farhi, E. & Gutmann, S. Quantum computation and decision trees. Phys. Rev. A 58, 915–928 (1998).
Ribeiro, P., Milman, P. & Mosseri, R. Aperiodic quantum random walks. Phys. Rev. Lett. 93, 190503.1–190503.4 (2004).
Oliveira, A. C., Portugal, R. & Donangelo, R. Decoherence in two-dimensional quantum walks. Phys. Rev. A 74, 012312.1–012312.8 (2006).
Di Franco, C., Mc Gettrick, M. & Busch, Th. Mimicking the probability distribution of a two-dimensional Grover walk with a single-qubit coin. Phys. Rev. Lett. 106, 080502.1–080502.4 (2011).
Romanelli, A. Distribution of chirality in the quantum walk: Markov process and entanglement. Phys. Rev. A 81, 062349.1–062349.6 (2010).
Schreiber, A. et al. Decoherence and disorder in quantum walks: from ballistic spread to localization. Phys. Rev. Lett. 106, 180403.1–180403.4 (2011).
Nayak, A. & Vishwanath, A. Quantum walk on the line. arXiv:quant-ph/ 0010117.1–0010117.20 (2000).
Grimmett, G., Janson, S. & Scudo, P. F. Weak limits for quantum random walks. Phys. Rev. E 69, 026119.1–026119.6 (2004).
Karski, M. et al. Quantum walk in position space with single optically trapped atoms. Science 325, 174–177 (2009).
Schmitz, H. et al. Quantum walk of a trapped ion in phase space. Phys. Rev. Lett. 103, 090504.1–090504.4 (2009).
Zähringer, F. et al. Realization of a quantum walk with one and two trapped ions. Phys. Rev. Lett. 104, 100503.1–100503.4 (2010).
Broome, M. A. et al. Discrete single-photon quantum walks with tunable decoherence. Phys. Rev. Lett. 104, 153602.1–153602.4 (2010).
Schreiber, et al. Photons walking the line: a quantum walk with adjustable coin operations. Phys. Rev. Lett. 104, 050502.1–050502.1 (2010).
Žutić, I., Fabian, J. & Das Sarma, S. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 76, 323–410 (2004).
Dyakonov, M. I. & Perel, V. I. Possibility of orienting electron spins with current. Sov. Phys. JETP Lett. 13, 467–469 (1971).
Dyakonov, M. I. & Perel, V. I. Current-induced spin orientation of electrons in semiconductors. Phys. Lett. A 35, 459–460 (1971).
Hirsch, J. E. Spin Hall effect. Phys. Rev. Lett. 83, 1834–1837 (1999).
Saitoh, E., Ueda, M., Miyajima, H. & Tatara, G. Conversion of spin current into charge current at room temperature: Inverse spin-Hall effect. Appl. Phys. Lett. 88, 182509.1–182509.3 (2006).
Konno, N. Quantum random walks in one dimension. Quantum Inf. Process. 1, 345–354 (2002).
Strauch, F. W. Connecting the discrete- and continuous-time quantum walks. Phys. Rev. A 74, 030301(R).1–030301(R).4 (2006).
Mulken, O. & Blumen, A. Continuous-time quantum walks: Models for coherent transport on complex networks. Phys. Rep. 502, 37–87 (2011).
Acknowledgements
The authors acknowledge the financial support of the Brazilian agencies FAPESB (project PRONEX 0006/2009) and CNPq. Both authors acknowledge also the National Institute of Science and Technology for Complex Systems.
Author information
Authors and Affiliations
Contributions
A.M.C.S. and R.F.S.A. designed research, performed calculations, analyzed results and wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Souza, A., Andrade, R. Coin state properties in quantum walks. Sci Rep 3, 1976 (2013). https://doi.org/10.1038/srep01976
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01976
This article is cited by
-
Negative correlations can play a positive role in disordered quantum walks
Scientific Reports (2021)
-
Quantum-inspired cascaded discrete-time quantum walks with induced chaotic dynamics and cryptographic applications
Scientific Reports (2020)
-
Fast and slow dynamics for classical and quantum walks on mean-field small world networks
Scientific Reports (2019)
-
The defect-induced localization in many positions of the quantum random walk
Scientific Reports (2016)
-
Quantum walk on the line through potential barriers
Quantum Information Processing (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.


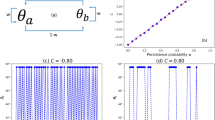

 between the numerical and the analytical results (Eq. (11)).
between the numerical and the analytical results (Eq. (11)). for typical values of θ. (b)
for typical values of θ. (b)  for η = 0. Symbols indicate numerical results while curves correspond to analytical results from Eq. (12).
for η = 0. Symbols indicate numerical results while curves correspond to analytical results from Eq. (12).


