Introduction

Since the beginning of banking the possibility of a lender to assess the riskiness of a potential borrower has been essential. In a rational world, the result of this assessment determines the terms of a lender-borrower relationship (risk-premium), including the possibility that no deal would be established in case the borrower appears to be too risky. When a potential borrower is a node in a lending-borrowing network, the node's riskiness (or creditworthiness) not only depends on its financial conditions, but also on those who have lending-borrowing relations with that node. The riskiness of these neighboring nodes depends on the conditions of their neighbors and so on. In this way the concept of risk loses its local character between a borrower and a lender and may become systemic. A systemically risky node in a financial network is one that – should it default – will have a substantial impact (losses due to failed credits) on other nodes in the network. Note that this notion of systemic risk is different from the risk of not getting payed back, the credit default risk.

The assessment of the systemic riskiness of a node turns into an assessment of the entire financial network1. Such an exercise can only be carried out with information on the asset-liability network. This information is, up to now, not available to individual nodes in that network. In this sense, financial networks – the interbank (IB) market in particular – are opaque. This in-transparency makes it impossible for individual banks to make rational decisions on lending terms in a financial network, which leads to a fundamental principle: opacity in financial networks rules out the possibility of rational risk assessment and consequently, transparency, i.e. access to system-wide information is a necessary condition for any systemic risk management. Note that recently an alternative notion for systemic importance of banks for the fluid transmission of credit through the IB market has been discussed in terms of “controllability”2.

The banking network is a fundamental building block in our globalized society. It provides a substantial part of the funding and liquidity for the real economy3. The real economy – the ongoing process of invention, production, distribution, use and disposal of goods and services – is inherently risky and introduces a third type of risk, the economic risk. This risk originates in the uncertainty of payoffs from investments in business ideas, which might not be profitable, or simply fail. This economic risk can not be eliminated from an evolving economic system, however it can be spread, shared and diversified. One of the roles of the financial system is to distribute the risk generated by the real economy among the actors in the financial network. The financial network can be seen as a service to share the burden of economic risk. By no means should this service by itself produce additional systemic risk on top of economic risk endogenously. Neither should the design and regulation of financial networks introduce mechanisms that leverage or inflate the economic risk. As long as systemic risk is endogenously generated within the financial network, this system is not yet properly designed and regulated. In this paper we show that, unless a certain level of transparency is introduced in financial networks, systemic risk will be endogenously generated within financial networks. Systemic risk is hard to reduce with traditional regulation schemes4,5. By introducing a minimum level of transparency in financial networks, endogenous risk can be drastically reduced without negative effects on the efficiency or volume in the financial services for the real economy. We think that the following results on systemic risk management hold generally. However, for demonstration purposes we use a specific setup of banks in the IB network that finance demands from the real economy.

Asset-liability or exposure data needed for systemic risk assessment in actual financial networks such as the IB market, does exist on various levels of reliability. In some developed countries IB loans are directly recorded in the ‘central credit register’ of central banks6,7. In several countries the exposure matrix can be estimated from IB payment data, as in8,9. The capital structure of financial agents, which is also necessary for systemic risk assessment, is available in most countries through standard reporting to central banks. Payment systems record financial flows with a time resolution of one second, see e.g.10. Several studies have been carried out on historical data of asset-liability networks6,9,11,12,13,14, including overnight markets15 and financial flows16. However, exposure networks, payment flows and balance sheets do not yet provide a complete picture. For a more complete view on the actual risk networks it would be necessary to integrate data of credit derivative (issuer-holder) networks and collateral networks (who holds what collateral for what loan). The true risk network is a multiplex network where the same set of financial agents is connected by various networks, including the asset-liability network, the derivative and the collateral network, posing significant data challenges. For simplicity, in this work we assume that it is possible (for central banks) to compute network metrics based on the asset-liability matrix at any time (as a proxy of the true systemic risk network), which in combination with the capital structure of banks, allows to define a systemic risk-rating of banks.

Network metrics can be used to systematically capture the fact that systemic risk spreads by borrowing. Borrowing from a systemically risky bank makes the borrower systemically more risky, since its default might tip the risky lender into default which then may cause system wide effects. These metrics are inspired by PageRank, where a web page, that is linked to a famous page, gets a share of the ‘fame’. A metric similar to PageRank, the so-called DebtRank, has been recently used to capture systemic risk levels in financial networks17. In this paper we present an agent based model of the IB network that allows to estimate the extent to which systemic risk can be reduced by introducing transparency on the level of the DebtRank. For computational efficiency we propose a measure based on Katz centrality18, which we refer to as Katz rank. Both are closely related to the concept of eigenvalue centrality19. Betweenness centrality has been used to determine systemic financial risk before12. To demonstrate the risk-reduction potential of feeding information of the DebtRank back into the system, we use a simple toy model of the financial- and real economy which is described in the next section. Interbank models of similar design were used before in different contexts20,21,22.

The central idea of this paper is to operate the financial network in two modes. The first reflects the situation today, where banks don't know about the systemic impact of other banks and where all IB credits are traded with the same interest rate, the so-called ‘inter bank offer rate’, rib. We call this scenario the normal mode.

The second mode introduces a minimum regulation scheme, where banks choose their IB trading partners based on their DebtRank. The philosophy of this scheme comes from the fact that borrowing from a systemically dangerous node can make the borrower also dangerous, since she inherits part of the risk and thereby increases overall systemic risk. Note, that a default of the borrower from a systemically dangerous bank affects not only the lender, but possibly also all other nodes from which the lender has borrowed. The idea is to reduce systemic risk in the IB network by not allowing borrowers to borrow from risky nodes. In this way systemically risky nodes are punished and an incentive for nodes is established to be low in systemic riskiness. Note, that lending to a systemically dangerous node does not increase the systemic riskiness of the lender. We implement this scheme by making the DebtRank of all banks visible to those banks that want to borrow. The borrower sees the DebtRank of all its potential lenders and is required (that is the regulation part) to ask the lenders for IB loans in the order of their inverse DebtRank. In other words, it has to ask the least risky bank first, then the second risky one, etc. In this way the most risky banks are refrained from (profitable) lending opportunities, until they reduce their liabilities over time, which makes them less risky. Only then will they find lending possibilities again. This mechanism has the effect of distributing risk homogeneously through the network and prevents the emergence of systemically risky nodes in a self-organized critical way: risky nodes reduce their credit risk because they are blocked from lending, non-risky banks can become more risky by lending more. We call this mode the transparent mode.

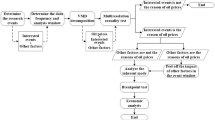
The model. The agents in the model are B banks, F firms and households. For simplicity every bank has only one firm as commercial client, F = B. This simplification is to some extend justified by the fact that for example in Germany the number of large corporations and the number of relevant banks are of the same order of magnitude23,24. In Fig. 1 we show a schematic structure of the model. For details of the implementation, see SI. At every timestep each firm approaches its main bank with a request for a loan. The size of these loans is a random number from a uniform distribution. Banks try to provide the requested firm-loan. If they have enough cash reserves available, the loan is granted. If they do not have enough, they approach other banks in the IB market and try to get the amount from them at an interest rate of rib. Not every bank has business relations with every other bank. Interbank relations are recorded in the IB bank-relation network, A. If two banks i and j, are willing to borrow from each other, Aij = 1, if they have no business relations, Aij = 0. We model the IB relation network with fully connected networks, random graphs and scale-free networks, see SI. A fully connected bank-relation network means that Aij = 1, for all pairs (i, j). In this case any bank can do business with any other and there is no special network topology or bias in business relations. If a bank does not have enough cash and can not raise the full amount for the requested firm-loan on the IB market, it does not pay out the loan. If the bank does pay out a loan, the firm transfers some of the cash to the households as ‘investments’ for future payoffs (wages, invest in new machines, etc.). Loans from previous timesteps are paid back after τ timesteps with an interest rate of rf–loan > rib. The fraction of the loan not used to pay back outstanding loans, ends up at the households (for details see SI).

Figure 1
figure 1

Schematic structure of the model.

Firms approach their bank for firm-loans. These loans are transferred to the households, where they are redistributed to other firms or are deposited in banks. If a bank can not service a firm-loan because it presently does not have the requested sum available in the bank, it tries to get the necessary funding through an interbank loan from an other bank. If it can get an IB loan, the firm-loan is payed out, if it can not, the firm will receive no loan.

Full size image

Households use the money received from firms to (1) deposit a certain fraction at the bank, for which they get interest of rh, or (2) to consume goods produced by other firms (details in SI). This money flows back to firms (the firms' profits) and is used by those to repay loans. If firms run a surplus, they deposit it in their bank accounts, receiving interest of rf–deposit. The two actions of the households effectively lead to a re-distribution and re-allocation of funds at every timestep. For simplicity we model the households as a single (aggregated) agent that receives cash from firms (through firm-loans) and re-distributes it randomly in banks (household deposits) and among other firms (consumption).

Specifically, at time t a bank-firm pair is chosen randomly and the following actions take place:

  1. i

    banks and firms repay loans issued at time t − τ

  2. ii

    firms realize profits or losses (consumption)

  3. iii

    banks pay interest to households

  4. iv

    firms request loans

  5. v

    households re-distribute cash obtained from firms

  6. vi

    liquidity management of banks in the IB market, including: IB re-payments, firm-loan requests, defaulted firms and re-distribution effects from households

  7. vii

    firms pay salaries and make investments

  8. viii

    firms or banks default if equity- or liquidity problems arise

A new bank-firm pair is picked until all are updated (random sequential update); then timestep t + 1 follows.

During the simulation, firms and banks may be unable to pay their debts and thus become insolvent. Firms are declared bankrupt if they are either insolvent, or if their equity capital falls below some negative threshold. Banks are declared bankrupt if they are insolvent, or have equity capital below zero. Negative equity of firms can result from a large loss (households do not buy there) or a series of losses on its investments. Negative equity of banks can arise through the bankruptcy of a firm or another bank and the subsequent failure of their loan repayments. See SI for details. If a firm goes bankrupt the bank writes off the respective outstanding loans as defaulted credits and realizes the losses. If the bank has not enough equity capital to sustain these losses it goes bankrupt as well. After the bankruptcy of a bank there occurs a default-event for all its IB creditors. This may trigger a cascade of bank defaults. For simplicity, there is no recovery for IB loans. This assumption is reasonable for the short run, which matters in practice for short term liquidity25. A cascade of bankruptcies happens within one timestep. After the last bankruptcy is taken care of, the simulation is stopped. We model a closed system of banks, firms and households, meaning that there are no in- or out-flows of cash from the model.

In the normal mode the model captures the current market practice, where banks follow a simple strategy to manage their liquidity. If a bank needs additional liquidity (for providing a firm-loan request, or for its own re-payments of IB loans) it contacts banks it is connected with in the IB relation network A and asks them for IB loans. In the normal mode, bank i asks its neighbors j (with ) in random order. If bank j can provide only a fraction of the requested IB loan, bank i takes it and continues to ask an other neighbor bank from (in random order) until the liquidity requirements of i are satisfied.

A simple modification to improve the stability of the system is to avoid borrowing from banks with a large systemic impact. For this a minimum level of transparency of the IB market is necessary. For all banks we compute systemic risk metrics based on the IB liability network Lij(t) and the equity of banks (t), at timestep t (details in SI). In particular we compute the DebtRank 17 and – for comparison – the Katz rank (see methods). The most risky bank has rank 1, the least risky has rank B, see methods.

In contrast to the normal mode, before bank i asks its neighbors for IB loans, it orders them (the banks contained in set ) according to their inverse Debt- or Katz rank. It then asks its neighboring banks in the order of their inverse rank, i.e. it first asks the least risky, then the next risky, etc. The rank is computed at the beginning of each timestep. In this way the low-risk banks are favored because the likelihood for obtaining (profitable) IB deals is much higher for them than for risky banks, which are at the end of the list and will practically never be asked.

In reality this implies that the banks know the DebtRank of each of their neighboring banks. This transparency is not available in the present banking system. Note however, that in many countries central banks have all the necessary data to compute the DebtRank. A possible way to implement such an incentive scheme in reality, is presented in the discussion.

We further implement a version of the transparent IB market, where the DebtRank is computed after every transaction that takes place in the IB market, instead of being computed at the beginning of the day. This version we refer to as the fast mode.

Results

We simulate the above model with the parameters given in SI, for 500 timesteps. Results are averages over 10,000 identical simulations. Fit parameters to the following distribution functions are collected in SI Table 2.

In Fig. 2 (a) we show the distribution of losses to banks for the the normal mode (red), where the selection of counterparties for IB loans is random and the transparent mode (blue), where banks sort their potential counterparties according to their inverse DebtRank and then approach the least risky neighbor first for the IB loan. The fast mode is shown in green. The normal mode shows a heavy tail in the loss distribution, which completely disappears in the transparent and fast modes, where there are no losses higher than 50 and 40 units, respectively. Of course losses do not entirely disappear in the transparent scheme, since the economic risk that firms bring to the banking system can not be completely eliminated. The fast mode appears to be slightly safer than the transparent mode. Fits to all curves are found in SI.

Figure 2
figure 2

Comparison of the normal mode (red), i.e. random selection of counterparty for IB loans, with the transparent IB market (blue), where the order of counterparty selection is determined by the inverse DebtRank.

The fast mode is shown in green. (a) Distribution of total losses to banks , (b) distribution of cascade sizes of defaulting banks and (c) distribution of transaction volume in the IB market . We performed 10,000 independent, identical simulations, each with 500 timesteps, 100 banks and the simulation parameters given in SI Table I. A is a fully connected graph.

Full size image

The distribution of cascade-sizes of defaulting banks is seen in Fig. 2 (b). Again the normal mode shows a heavy tail, meaning that in a non-negligible number of events, defaults of a single bank trigger a cascade of liquidity and equity problems through the system. In some cases up to 80 % of the banks collapse. In the transparent mode the likelihood for contagion is greatly reduced and the maximum cascade size is limited by 40 banks in the transparent and about 30 in the fast mode.

In Fig. 2 (c) we show the transaction volume in the IB market of the three modes, normal (red), transparent (blue) and fast (green). The transparent and fast modes show a higher transaction volume indicating a more efficient IB market, where liquidity from banks with excess funds is more effectively channeled to those without. We verified, that the ratio of requested- to provided firm-loans, the efficiency , yields ~ 1, irrespective of the mode.

In Fig. 3 we show the normalized DebtRank for all individual banks, for the normal (red) and the transparent scheme (blue). Banks are rank-ordered according to their DebtRank so that the most risky bank is found to the very left, the safest to the very right. It is clear that the systemic risk impact in the transparent mode is spread more evenly throughout the system, whereas in the normal mode some banks appear to be much more dangerous to the system.

Figure 3
figure 3

Normalized DebtRank, for individual banks in the normal (red) and the transparent mode (blue).

Banks are ordered according to their DebtRank, the most risky is to the very left, the safest to the very right. The distribution is an average over 1000 simulation runs with an ER network and shows the situation at timestep t = 100.

Full size image

In Fig. 4 we compare the losses for DebtRank (red) and Katz rank (blue). The performance of the two definitions is hardly distinguishable. Also the other systemic risk measures show no noticeable difference, for cascade size and transaction volume distributions , see SI.

Figure 4
figure 4

Comparison of the performance of the DebtRank (red) and the Katz rank (blue) for the losses, .

Both rank definitions provide practically identical results. Same simulation parameters as in previous figure.

Full size image

Figure 5 shows the distribution of losses , for the (a) normal and (b) transparent mode, as computed with an Erdös-Rényi (ER) contact network (red) with γ = 0.115 and a scale-free (SF) network (produced with the Barabási-Albert algorithm, see SI) with the same average connectivity (〈k〉 = 11.5). In both modes the SF network leads to a slightly riskier situation. The situation for cascade sizes and transaction volume is depicted in SI Fig. 3, where we also show and discuss the effects of connectivity on the three measures in SI Fig. 4.

Figure 5
figure 5

Distributions of losses for the normal (a) and transparent mode (b), for an ER (red) and a SF network (blue), both with the same average connectivity 〈k〉 = 11.5.

Full size image

We compute the distribution of the time to first default , for the normal and the transparent modes. Both distributions are practically Gaussian (kurtosis ~ 3.3, skewness ~ 0.4) with mean and standard deviation of and , respectively. This is expected, since typically the first default is triggered by a firm-default, which is (to first order) independent of the situation in the IB market, but only depends on the parameters describing the firms (μi, σreturn, Cdefault) and households (σ, ρ), see SI.

Finally, in Fig. 6 we show the effect of the bank selection process induced by the transparent mode on the IB liability network topology. The distributions of in-degrees k of the IB liability network sgn(Lij) for the normal (red) and transparent mode (blue) are shown at timestep t = 100 for a totally connected bank-relation network, Aij = 1 for all ij. The in-degree of sgn(Lij), for bank i is the total number of different banks, i has granted loans to within the last τ timesteps. In the normal mode (random order of loan requests) the emerging liability network shows a Poisson distributed in-degree distribution (green), with λ = 2.14. The IB network topology of the normal node nicely coincides with the expected result from random linking. On average, half of the banks have excess liquidity and can provide loans to other banks. In the transparent mode only banks with a low DebtRank provide IB loans. This leads to fewer banks lending on the IB market and is reflected in Fig. 6 by the high number of nodes with an in-degree of zero. The total demand for IB loans (which is approximately the same as in the normal mode) is now serviced by fewer banks with a low DebtRank. As a result, the in-degree distribution of the transparent mode broadens and is well fitted by a Weibull distribution with a = 7.13 and b = 1.62 (green). Regardless of the number of links, a bank with a low DebtRank, i.e. a bank that has borrowed little or nothing on the IB market, is not systemically risky. The out-degree distribution (total number of different banks a bank has received loans from) is mainly influenced by the cash needs of a bank. Therefore the out-degree distribution in the transparent mode is similar to the in-distribution in the normal mode, which is shown in SI Fig. 2.

Figure 6
figure 6

Distributions of in-degrees k of the IB liability network sgn(Lij) for the normal (red) and transparent mode (blue), for the case where the bank-relation network was fully connected (Aij = 1 for all ij).

The in-degree distribution (total number of different banks, a bank has granted loans to) is affected in the transparent mode because only banks with a low DebtRank provide loans to others. For the normal mode the distribution can be well fitted by a Poisson with λ = 2.14; the transparent mode is better fitted with a Weibull distribution with a = 7.13 and b = 1.62 (green lines). The distributions are an average over 1000 simulation runs and shows the situation at time t = 100.

Full size image

Discussion

We showed that the systemic risk, endogenously created in a financial network by the inability of banks to carry out correct risk-estimates of their counterparties, can be drastically reduced by introducing a minimum level of transparency. This becomes possible by introducing an incentive that makes borrowers more prone to borrow from systemically safe lenders. As a measure of the fraction of systemic risk of individual agents we use network centrality measures, such as the DebtRank and make it available to all nodes in the network at each point in time. We could show that the efficiency of the financial network with respect to the real economy is not affected by the proposed regulation mechanism. For this we verified that neither the volume of credit to firms (real economy) was reduced or lowered in the transparent scheme ( ~ 1 in all modes), nor that the trading volume in the IB market was lower than in the normal mode. On the contrary we could even find a slight increase in trading volume in the transparent mode. Maintaining of efficiency is possible since the regulation re-distributes risk in order to avoid the emergence of risky agents that might threaten the system and does not reduce the trading volume in the real economy or in the IB liability network. Risky nodes that are low in DebtRank, are barred from the possibility of lending their excess reserves to others. This deprives them from making profits on IB loans, but also reduces their risk of being hit by defaulted credits. They only receive payments and do not issue more risk, meaning that over time they become less risky. Less risky banks are allowed to take more risk (lend more) and make more profits. The proposed mechanism makes the system safer in a self-organized critical manner. We explicitly show how this selection process re-shapes the IB network from a random graph in the normal mode to a fat tailed degree distribution in the transparent mode.

Note, that in our scheme the borrower determines who borrows from whom. Usually the lender is concerned if the borrower will be able to repay the loan. However, this credit default risk is not necessarily of systemic relevance. Lending to a bank with a large systemic risk can have relatively little consequences for the systemic importance of the lender, or the systemic risk of the system as a whole. In contrast, if a bank borrows from a systemically dangerous node the borrower inherits part of this risk and increases the overall systemic risk. These facts are conveniently incorporated in the definition of the Debt- and Katz rank.

We found that the performance of the method is surprisingly insensitive to the choice of the particular centrality measure, or to the actual topology of the IB relation network (scale-free or random). Also the average connectivity of the network is not relevant, as long as it remains in sensible regions . This suggests that the essence of the proposed scheme is that risk is spread more evenly across the network, which practically eliminates cascading failures.

A way to implement the proposed transparency in reality would be that central banks regularly compute the DebtRank of the asset-liability network (as reported or inferred from payment systems) and make it available to all banks. To enforce the regulation, the central bank could monitor IB loans through the payment system and severely punish borrowers who failed to find less risky lenders. Note however, that the asset-liability network is only an approximation to the true risk network which is a multiplex network, meaning that the banks are linked by at least three risk-relevant networks: the asset-liability, the credit derivative and mutual collateral-holding networks. To derive practicable effective risk networks from the multiplex poses future technical challenges. A more market driven mechanism to obtain the same self-organized critical regulation dynamics is subject to further investigations. For future work it would be interesting to study the aspects of “contrability” introduced in2 within the context of the presented transparency scheme. Currently, banks have no incentive whatsoever to disclose their systemic risk levels to others and one could only force them to do so, or – formulated more positively – create appropriate incentives. This is maybe only possible with changes in the current jurisdiction.

Methods

DebtRank

DebtRank is a recursive method suggested in17 to determine the systemic relevance of nodes in financial networks. It is a number measuring the fraction of the total economic value in the network that is potentially affected by a node or a set of nodes. Let Lij denote the IB liability network at a given moment (loans of bank j to bank i) and Ci is the capital of bank i, see SI. If bank i defaults and can not repay its loans, bank j loses the loans Lij, see SI. If j has not enough capital available to cover the loss, j also defaults. The impact of bank i on bank j (in case of a default of i) is therefore defined as

Given the total outstanding loans of bank i, , its economic valve is defined as . The value of the impact of bank i on its neighbors is . To take into account the impact of nodes at distance two and higher, it has to be computed recursively,

where β is a damping factor. If the network Wij contains cycles the impact can exceed one. To avoid this problem an alternative was suggested17, where two state variables, hi(t) and si(t), are assigned to each node. hi is a continuous variable between zero and one; si is a discrete state variable for 3 possible states, undistressed, distressed and inactive, . The initial conditions are , ; hi(1) = 0, and si(1) = D, ; si(1) = U, (parameter Ψ quantifies the initial level of distress: , with Ψ = 1 meaning default). The dynamics of hi is then specified by

The sum extends over these j, for which sj(t − 1) = D,

The DebtRank of set Sf (set of nodes in distress at time 1), is and measures the distress in the system, excluding the initial distress. If Sf is a single node, the DebtRank measures its systemic impact on the network. The DebtRank of Sf containing only the single node i is

The normalized DebtRank is .

Katz rank

The Katz centrality can be used to capture the risk of contagion in IB networks and is defined as

To ensure that the Katz centrality converges, we set α = 1/κ1, where κ1 is the largest eigenvalue of Lij. The overall multiplier β is not important, for convenience we set β = 1. We define the Katz rank in the following way: the most risky bank i, with the highest Katz centrality gets Katz rank , the least risky bank j (lowest Katz centrality) gets . Note, that banks that only borrow (in-links only) may cause contagion and have non-zero Katz centrality. Banks that only provide loans (out-links) have zero Katz centrality. Loan sizes, neighbors and their neighbors, etc., are included in the centrality.

Systemic risk measures

For measures of systemic risk in the system, we use the following three observables: (1) time to first default as the timesteps of the simulation before the first default of a bank occurs, , (2) the size of the cascade, as the number of defaulting banks triggered by an initial bank default and (3) the total losses to banks following a default or cascade at t0, .

Efficiency measures

To quantify the efficiency of the banking system we use the ratio of the sum of requested loans by the firms to the sum of loans actually payed out to firms, at a given time t, averaged over time,

The efficiency of the system is then the time average , taken over the simulation. As another measure of efficiency we use the transaction volume in the IB market at a particular time t = T in a typical simulation run,

The first term represents the new IB loans at timestep T, the second the loans that are repaid. We set T = 100.