Abstract
Animal behaviour exhibits fractal structure in space and time. Fractal properties in animal space-use have been explored extensively under the Lévy flight foraging hypothesis, but studies of behaviour change itself through time are rarer, have typically used shorter sequences generated in the laboratory and generally lack critical assessment of their results. We thus performed an in-depth analysis of fractal time in binary dive sequences collected via bio-logging from free-ranging little penguins (Eudyptula minor) across full-day foraging trips (216 data points; 4 orders of temporal magnitude). Results from 4 fractal methods show that dive sequences are long-range dependent and persistent across ca. 2 orders of magnitude. This fractal structure correlated with trip length and time spent underwater, but individual traits had little effect. Fractal time is a fundamental characteristic of penguin foraging behaviour and its investigation is thus a promising avenue for research on interactions between animals and their environments.
Similar content being viewed by others
Introduction
Fractal structure characterizes a diverse array of natural systems, from coastlines, DNA sequences and cardio-pulmonary organs, to temporal fluctuations in temperature, heart rate and respiration1,2,3,4,5,6,7,8,9,10,11. Spatial and temporal patterns of animal behaviour have also been described as fractal, exhibiting self-similarity or self-affinity across a range of measurement scales. For example, fractal movements (a.k.a. Lévy walks) are super-diffusive and thus theoretically adaptive in heterogeneous and unpredictable environments where they can enhance the probability of resource encounters over Brownian (random) movements (Lévy Flight Foraging Hypothesis)12,13,14,15. In the temporal domain, various physiological impairments or other challenges can lead to complexity loss in behavioural sequences, i.e. increased periodicity or stereotypy16,17,18,19,20,21. The latter is congruent with studies of altered physiology in stress and disease in humans, which have underpinned the hypothesis that fractal structure is adaptive because it is more tolerant to variability extrinsic to the biological or physiological system producing it4,6,11,22,23. Fractal analysis can thus help us understand the structure and function of animal behaviour.
However, while exploring fractal properties in spatiotemporal data is currently a hot topic in the movement ecology literature, less attention has been paid to strictly temporal fluctuations in behaviour, despite that the first studies of fractal time appeared nearly two decades ago19,24,25,26 and that temporal complexity has been linked to individual quality or health (see above). There are two main obstacles to assessing fractal time in behaviour sequences. First, generating sufficiently long time series to perform meaningful analyses is no easy task because accurately recording behaviours continuously is difficult, particularly under natural conditions; all but 3 studies of fractal time were experimental16,17,27. There is debate about whether fractal analyses apply to shorter sequences because scaling is theoretically asymptotic28,29,30,31 and while the methods used may be sensitive to long-range dependence they may not always be specific, i.e. one can always find a higher order short-range correlated model to describe apparently fractal patterns32,33. Furthermore, irrespective of sequence length, single values produced by fractal analysis to characterize observed sequences by their long-range correlative properties (i.e. scaling exponents) may not represent the entire range of measurement scales examined; scaling exponents may be scale-dependent rather than scale-independent as theoretically predicted34,35. While scale-dependency can undoubtedly provide useful information about animal responses to salient features at various scales36,37,38,39, multiple scaling regions means that single exponents cannot accurately characterize their behaviour. Alternatively, log-log plots of fluctuation as a function of scale, upon which calculation of scaling exponents is typically based, may appear linear even in the absence of scaling35,40,41. Unfortunately, few – if any – studies of fractal time in animal behaviour have critically addressed these issues sensu34,35, leaving questions about the robustness of their results.
In this study, we address these issues by applying fractal analysis to binary sequences of foraging behaviour (i.e. diving and the gaps between successive dives) collected via bio-logging from a marine predator. Bio-logging can be described as the use of animal-attached devices to investigate “phenomena in or around free-ranging organisms that are beyond the boundary of our visibility or experience”42. This approach is indispensable for monitoring behaviours of animals that cannot be systematically observed because accurate records of various behavioural parameters can be attained at fine time scales over long periods43,44. In addition to increasing the robustness of fractal results, such lengthy sequences allow us to better assess the fit of the regression line in the double logarithmic plot and thereby test for its accuracy and the potential for multiple scaling regions. In one of the first investigations of fractal time, the authors note that identifying fractal scaling in the behaviour of their study subjects (Drosophila melanogaster) was only possible following the development of technology capable of accurately recording behaviour at previously unavailable resolutions (i.e. 0.1 s in this case)25. Bio-logging technology offers similar advantages for the study of fractal properties in temporal sequences of wild animal behaviour and we expect this merger of techniques to yield valuable information about general qualitative properties in sequences of animal behaviour in situ.
We were able to use behaviour sequences of little penguins (Eudyptula minor) spanning complete foraging trips, ca. 50,000 data points at 1 second sampling intervals (215 ~ 216 points across ca. 15 hours); among the longest continuous binary sequences of animal behaviour that have been used in studies of fractal time. Such waveform behaviour sequences can mitigate some issues concerning sequence length because data can be recorded at very fine resolutions (e.g. <1 s)18,25,45. Previous studies using this approach have examined behavioural sequences with 211 or 212 total data points16,17,27,46,47, but total observation periods have typically remained in the range of ca. 30–60 minutes, i.e. 2048–4096 data points, with few exceptions27. Short sequences such as these can be problematic under natural conditions because animal activity patterns tend to occur in rhythms with strong temporal variation in behavioural performance. Context-specific (e.g. within bout) analyses of complexity can provide useful information16, but they do not allow us to assess correlational properties at larger time scales incorporating multiple bouts and modes of behaviour.
We employed 4 fractal analytical methods to avoid potentially misleading results that can occur when relying on any single method48,49, including Detrended Fluctuation Analysis (DFA; both linear- and bridge-detrended versions), the Hurst Absolute Value method and the Box-counting method to determine whether temporal sequences of penguin behaviour are consistent with patterns expected if they were generated by a long-memory process characterized by scaling. We examine whether a single scaling exponent can characterize entire foraging sequences, whether scaling is restricted to a certain range of scales within these sequences, or whether multiple scaling regions must be considered. We then use the scaling exponents generated to test whether general differences exist in relation to individual traits (age, sex, chick age and body mass) and whether the various methods produce consistent results across individuals. Finally, we compare these results with those generated by more traditional, frequency-based approaches commonly used to quantify marine animal foraging behaviour.
Results
Frequency-based dive parameters
During the study period, little penguin foraging trips lasted for a mean ± s.d. of 14.8 ± 0.9 hours (range: 12.1–16.9). Within each foraging trip, penguins spent 35.4 ± 10.6% of the time underwater (range: 21.3–55.4). Individual dives within the sequence lasted for a mean ± s.d. of 29.8 ± 6.3 seconds (mean range: 20.0–39.9), with mean dive depths of 12.3 ± 3.0 meters below the surface (mean range: 4.9–16.8). Correlations between these dive parameters are shown in Fig. 1a.
Correlations between diving parameters for both (a) frequency-based and (b) fractal measures.
Lower-left panels show correlation scatterplots while upper-right panels give Pearson's correlation coefficients along with their respective confidence intervals. Measurement types are shown diagonally between these panel blocks.
Scaling exponents
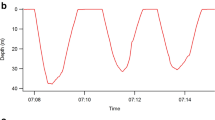
All fractal measures point to the existence of temporal scaling in observed sequences of penguin foraging behaviour. The mean ± s.d. scaling exponents were: αDFA = 0.88 ± 0.06; αDFAb = 1.89 ± 0.05; HAV = 0.80 ± 0.06; Db = 1.10 ± 0.07. Examination of αDFA shows that the original binary sequences (example shown in Fig. 2a) were characteristic of fractional Gaussian noise (fGn: αDFA ∈ (0,1)), which was confirmed by the fact that the integrated sequences (examples shown in Fig. 2b) measured via DFAb produced αDFAb ∈ (1,2), characteristic of fractional Brownian motion (fBm). Furthermore, our estimates of the Hurst exponent H using αDFA and αDFAb are in agreement with the expected theoretical relationships (αfGn ≈ αfBm−1) and the Pearson correlation coefficient of 0.93 for values of αDFA and αDFAb further confirms their compatibility (Fig. 1b). Agreement between other measures was fair, ranging between absolute values of |0.66| and |0.89| for all other combinations. Negative correlations involving Db were predicted by the inverse relationship expected between Hurst and fractal dimension estimates. Finally, that 0.5 < H < 1 for all estimates of H clearly suggests that little penguin foraging sequences are characterized by persistent long-range dependence (positive autocorrelation); i.e. behavioural patterns tend to persist across long time frames and scale accordingly, although they did not persist across all scales examined (see below). Note that all scaling exponents presented above were calculated using the best scaling region which is derived in the next section.
Example of (a) a single little penguin female's binary foraging sequence denoted 1 for diving and −1 for lags between successive dives and (b) integrated (cumulatively summed) dive sequences from 5 different little penguin females showing variation in foraging patterns and resultant changes in αDFA values.
The bold solid line indicates the integrated dive sequence corresponding to the binary sequence shown above.
Validation of scaling regions
A closer examination of the log-log plot of F(n) versus n in DFA shows that scaling does not persist across all scales examined (Fig. 3). The R2 – SSR procedure demonstrates that the best scaling region lies between 27 ~ 212, ca. 128 ~ 4096 s or 2.1 ~ 68.3 min (Fig. 3A, B). However, the compensated slope procedure places values at the 2 largest scales within the range of variation expected given some element of noise (Fig. 3C) and thus scaling may persist to 214, 16384 s or 273.1 min, spanning more than 2 orders of magnitude; i.e. a similar correlation structure is found at all of these measurement scales. To be conservative, we calculated scaling exponents using only the range of scales included in the best scaling region by both methods, i.e. 27 ~ 212. If on the other hand we relied only on R2 values as many previous studies have done, we might have included all scales in this region given that all values were greater than 0.997 in DFA across sequences using all scales examined (Fig. 3) and given the similar mean values of αDFA using the best and full range of scales (0.877 and 0.865, respectively).
Validation of scaling regions in sequences of diving behaviour from little penguins.
(A) The R2 – SSR procedure determines the values of log(scale) that maximize the coefficient of determination and minimize the sum of squared residuals (*), corresponding to the range of scales across which the data reflect strong scaling behaviour (filled circles shown in (B)). Note that when all scales are used (+) the coefficient of determination remains comparable to that of the best scaling region, indeed all regression fits produced R2 values greater than 0.997, but the sum of squared residuals increases dramatically. In this case, the estimates of αDFA for the best scaling region and the full range of scales are also comparable at 0.877 and 0.865, respectively. (C) The compensated slope procedure allows testing the effect that varying the scaling exponent has on dispersion around a “zero-slope” (solid line), the point at which the scaling exponent is a true representation of the sequence. The scaling exponent derived from the best scaling region produces values that best approximate a zero-slope (Δ), with all points examined falling within the 95% confidence intervals (dotted lines) generated by 1000 simulations of random variation around a zero-slope. Therefore, these observed sequences do exhibit fractal structure with power-law scaling behaviour, i.e. strong linearity in the log-log plot of fluctuation as a function of scale, at least across the scales outlined in (B).
Increasing the sampling resolution from 1 s to a maximum of 30 s did not significantly alter resultant αDFA values, despite that total sequence lengths decreased from a mean of 54000 data points to ca. 10800, 5400, 2700 and 1800 for 5, 10, 20 and 30 s intervals, respectively. Values of αDFA were 0.88 ± 0.06, 0.88 ± 0.06, 0.87 ± 0.07 and 0.84 ± 0.08 when using the best scaling regions from each set of sequences, respectively. Pearson correlation coefficients for comparisons between these and values from the 1 s interval sequences were 0.88, 0.86, 0.84 and 0.87. There was also considerable overlap in their best scaling regions. However, while scaling was found to begin at ca. 2 min when using the higher-resolution 1 s sequences, the lower-bound limits of the scaling region were higher in all of these lower-resolution sequences (range: ca. 4–5 min). Conversely, the R2 – SSR procedure included slightly larger upper-bound limits for the 5, 10 and 20 s interval sequences, extending to ca. 85 min in each case (respectively 1024, 512 and 256 data points) as opposed to the ca. 68 min scaling limit (4096 data points) for 1 s intervals. Perhaps because of the considerably shorter sequence lengths, scaling regions in the 30 s interval sequences capped at ca. 64 min (128 data points), as did the 1 s interval sequences. Like the original results, the compensated-slope procedure applied to these sequences also included all of the largest scales in the best scaling region, pushing the potential upper-bound limit of the scaling region to over 340 min from the 273 min estimated above.
Variation in scaling exponents and frequency-based dive parameters
Individual differences between study subjects could not explain any significant portions of the variation in either scaling exponents (Table 1) or summary statistics (Table 2) from observed foraging trips, with one exception: initial body mass was positively associated with scaling exponents generated by DFAb. Because αDFAb is inversely related to fractal dimension, this result suggests that birds with greater body mass at the beginning of the foraging trip performed less temporally complex dive sequences than did initially lighter birds. However, none of the three other fractal measures produced similarly significant relationships between these variables, although the effect size was indeed largest for body mass in all cases. Therefore, while the relationship between body mass and complexity must remain equivocal until further data can be examined, we observed fair agreement across measures in the effects of these four variables on complexity.
We observed a number of associations between frequency-based dive parameters and scaling exponents (Table 3). First, total time spent underwater had a significant positive effect on exponents measured by DFA and DFAb and the inverse effect on the box-counting dimension; i.e. complexity increased with dive time in all three cases. Given that time spent underwater ranged from ca. 21–55% across foraging trips, these results mimic those from the simulated sequences in which αDFA increased as the probability function diverged from 50–50 (see Supplentary Table S1). However, since randomized surrogate sequences analysed by DFAb and box-counting all produced H = 0.5 (see Supplentary Information), the effect of total time spent underwater on these scaling exponents cannot be explained completely by such altered distributional characteristics. Second, trip durations were positively associated with both DFAb and HAV; i.e. complexity decreased with sequence length using these indices. Finally, we found a negative association between mean dive duration and αDFAb, but no relationship between this summary statistic and other fractal measures. Similarly, mean dive depth, which was highly correlated with mean dive duration (0.9 in all model correlation matrices), was unrelated to observed scaling exponents. Note that despite the strong positive correlations between these two variables, we found no evidence for excessive variance inflation (<10 in all cases) and have therefore left all terms in the statistical models. The weight of evidence therefore suggests that dive sequence complexity may well be associated with total time spent underwater and foraging trip duration, but is generally independent of both mean dive duration and depth.
Discussion
We demonstrated that binary sequences of little penguin foraging behaviour resemble patterns expected if they were produced by a long memory process characterized by temporal scaling; binary sequences were consistent with fractional Gaussian noise (fGn: 0 < H < 1) while integrated sequences were consistent with fractional Brownian motion (fBm: 1 < H < 2). Scaling exponents of all analyses fit their expected theoretical relationships, fell in the range 0.79 < H < 0.9 and therefore suggest strong persistence in dive sequences. In other words, any given region within a dive sequence is dependent upon patterns that occurred much earlier in the sequence, more so than would be expected of stochastic or even short-range dependent sequences. The persistence of the autocorrelation means that long diving events tend to be followed by long diving events and vice versa. Upon closer examination of the local slopes produced by the log-log plot of fluctuation as a function of scale using DFA, the data indicate that the best-scaling region ranged from windows of 27 (2 min) ~ 212 (68 min) or 214 (273 min), which in the latter case would constitute temporal scaling across more than 2 orders of magnitude, a rarity among behavioural studies. Within this range of scales, therefore, there is no single scale at which dive sequences can be fundamentally measured or distinguished.
In this way, our results correspond well with the many recent studies that have demonstrated fractal patterns in the Lévy-like movement paths of various marine animals. This indicates a search strategy which approximates theoretically optimal behaviour, allowing an organism to maximize its encounter rates with resources under heterogeneous conditions13,14,15,50,51. Thus we return full circle to the original studies of fractal time in animal behaviour which first demonstrated the link between resource distribution and temporal complexity25,26. Further investigation in the temporal domain is now warranted on at least two key accounts. First, studies such as ours, while admittedly ignoring the spatial location of an organism, focus on behavioural performance itself, in this case the sequential distribution of diving inclusive of changes in behavioural state, which may better address actual prey search and pursuit than does simple spatial data. In fact, fractal patterns in the distribution of any relevant behaviour through time can be investigated using this approach and to date, studies have investigated not only foraging and movement but also vigilance, posture and even reproductive and social behaviours16,17,18,20,27,52. The fact that animals do engage in multiple behaviours may make simple interpretation of sequential patterns in any given behaviour problematic. In this respect, seabird foraging behaviour provides a particularly useful model system for studies of fractal time, with switches between periods that crudely consist of prey search/pursuit and surface recovery53,54; two clearly contrasting and mutually exclusive behaviours sensu55 and characteristic of behavioural intermittence56. Still, for marine birds and pinnipeds, temporal patterns of behaviour must arise not only as the outcome of prey encounters and distributions, but also of physiological limitations related to respiration57. Scaling exponents therefore represent behavioural complexity in a global rather than specific sense, resulting from multiple interacting variables, which would be expected of any complex adaptive system.
Second, there is a growing body of evidence suggesting that various stressors can lead to loss of complexity in behaviour sequences, i.e. the progression of behaviour through time becomes more periodic or stereotypical. This also suggests that scaling exponents can be used to characterize some aspect of individual or environmental quality. A number of studies have tested this hypothesis, showing that impairments or challenges ranging from parasitic infection through toxic substance exposure to increased exposure to anthropogenic disturbance16,17,18,19,20,21,27,58 are all associated with such complexity loss16,17,18,19,21,58. This may have major implications concerning the viability of individuals operating in a sub-optimal state. It will be interesting to determine whether similar examples of complexity loss can be demonstrated using spatial data collected from challenged individuals. Although the animal movement ecology literature on statistical patterns of search is growing with reference to optimality and response to environmental cues, little attention has been paid to intrinsic factors that might cause variation in scaling across individuals under the same ecological conditions55. Indeed, there seems to be a divide in the current literature in which spatial patterns (animal locations through time) and temporal patterns (behavioural changes through time) are generally discussed in relation to extrinsic (e.g. landscape variables) and intrinsic (e.g. health states) control mechanisms, respectively. Integration of these two domains and the framework through which their results are interpreted should therefore be a goal of future research, to further our understanding of how animals respond to scales in both time and space and to investigate whether complexity loss is a feature of both.
A key result of our study, however, is that scaling did not persist across all scales examined, a common limitation of using this approach to characterize complete sequences. Indeed, this has been a major criticism of using fractal analysis in studies of animal behaviour in the past59,60, although this criticism has been rebutted persuasively34, largely because previous studies had not critically assessed the data upon which their scaling exponents were based. In the present study, the lack of clear scaling at smaller scales likely reflects a combination of: (1) the influence of the mean individual dive durations, which were larger than most of these smaller scales at 29.4 ± 20.6 s; (2) decay of the strong short term autocorrelation; and, (3) mathematical error when small numbers of data points are used in regression analyses. At the largest scales, it is impossible to determine whether the bias in scaling is due to its absence or simply the paucity of available windows, i.e. an artefact of finite sequence length. This can only be answered by collecting sequences of greater length, which should continue to be a goal in future studies. What is promising, however, is that changing the resolution of the data did not lead to significant changes in the fractal properties of observed sequences, although our results do suggest that higher- and lower-resolution sequences may be better at detecting the presence of scaling at small and large scales, respectively.
In addition to these measurement-related issues, there may be biological reasons to expect changes in the correlation structure of foraging sequences at certain scales. This may in part reflect certain habitat characteristics and how animals interact with their environments at different scales. For example, the tortuosity of foraging paths in wandering albatross (Diomedea exulans) differs across three scaling regions: patterns at the smallest scales (~100 m) reflect adjustment to wind currents, at medium scales (1–10 km) food-search behaviour and at the largest scales (>10 km) long-distance movement between patches and change in local weather conditions61. For central place foragers like the penguins studied here, travel between foraging sites and the colony, which can constitute a considerable portion of the total sequence length (trip duration), may lead to scaling breaks at large scales. However, this cannot explain the deviation from scaling we observed at large scales because our sequences began only when the first instances of diving were observed, eliminating any effects of such movement types. Landscape heterogeneity can also affect scaling in animal movements, such as in American martens (Martes americana) where movement paths are determined by microhabitat features at small (<3.5 meters) but not larger scales38 and in grazing ewes where such features affected movements at scales greater than a threshold value (5 meters)39. While addressing variation in microhabitat structure is beyond the scope of the current study, prey locations are likely to have contributed strongly to deviations from scaling at small scales. This would be compounded in seabirds by the necessary pauses in foraging as animals return to the surface to breathe57. Strong short-term autocorrelation can result from bouts in which animals dive to similar depths in pursuit of prey within a patch and then surface to replenish oxygen reserves before repeating the process62.
In addition to the distinction between real and perceived scaling breaks, another difficulty in inferring fractal structure is that it is generally always possible to find a short-range correlated model of higher order and complexity to fit any sequence with finite length33; i.e. all real world data. For example, DFA failed to distinguish between a real long-range dependent process and a short-range one generated by the super-position of three first-order autoregressive processes32. In real-world data, simple autoregressive models have been used to predict the correlation structure of sequential dive depths in macaroni penguins (Eudyptes chrysolophus) with some precision63. However, other recent evidence also using successive measurements of dive depths strongly suggests that such sequences are rather consistent with long memory processes in most cases15,50,51. Indeed, short-range correlations cannot adequately model many biological and physical phenomena found in nature, which is why more parsimonious models of long-range dependence were developed33. Our study is among the first to examine binary time series of animal behaviour with lengths up to 216, sequences spanning 4 orders of magnitude and thus nearing and in some cases even exceeding those used in many simulation studies. Therefore, our results offer compelling support for long-range fractal structure in penguin dive sequences.
Ultimately, while describing the scaling exponents of behavioural sequences accurately is a fundamental component of this research, what may be of more interest to many researchers is the next step; the ability to apply such quantifiable properties in distinguishing between the behaviours of various groups of individuals or taxa. In this regard, our study did not show any clear differences in the complexity signatures of individuals in relation to age, sex, or chick age and produced only weak evidence for an effect of initial body mass. Similarly, these variables also did not affect any of the summary statistics measured. There is considerable variation across studies in the impacts of such biological factors on seabird behaviour64,65,66,67, so it remains difficult to make any strong inferences based on as small a data set as that used here. However, it is clear that certain aspects of foraging behaviour such as time spent underwater and trip duration can be correlated with dive sequence complexity. Our simulated data show that DFA can be sensitive to variation in the probability distribution of dives, but further analysis of the scaling region easily distinguished between simulated and observed behaviour (see Supplementary Information). Furthermore, reshuffling the dives produced random sequences in 3 of our 4 fractal methods, all of which correlated well with DFA, particularly DFAb. Together, these results suggest that time spent underwater and trip duration cannot on their own explain the variation in fractal scaling observed. It is also notable that neither mean dive duration nor depth was related to a sequence's fractal properties. Therefore, the sequential distribution of dives within a sequence is ultimately the key factor, adding weight to our assertion that temporal fractal analyses provide a metric that describes a fundamental property in animal behaviour: fractal time26.
In conclusion, we show here that penguin dive sequences exhibit a complex fractal structure through time and relate this structure to a combination of extrinsic (environmental) and intrinsic (self) organizational control elements. The application of fractal tools to temporal sequences of animal behaviour should be explored further, particularly in, though far from limited to, organisms that are often used as indicator species for climate and environmental change, like the penguins examined here and many other top predators in marine ecosystems. The merger of bio-logging and fractal analysis represents an important opportunity to do so, promising to advance our understanding of the many interactions that occur between animals and the environments in which they are found.
Methods
Study site & subjects
This study was conducted during the guard stage of the 2010 breeding period (October 26 – November 26) with free-living little penguins (Eudyptula minor) at the Penguin Parade, Phillip Island (38°31′S, 145°09′E), Victoria, Australia. Birds from this colony were marked with injected passive RFID transponders (Allflex, Australia) as chicks68. We collected diving data consisting of single full-day foraging trips from 28 penguins, 14 males and 14 females, guarding 1- to 2-week-old chicks. Each penguin's age was determined from the date of transponder injection. Sex was determined using bill depth measurements69. We captured the birds in artificial wooden burrows and fitted them with time-depth data loggers (ORI400-D3GT, Little Leonardo, 12 × 45 mm, 9 g) set to record depth to a resolution of 0.1 m with an accuracy of 1 m (range: 0–400 m) at one-second intervals. Devices were attached using waterproof Tesa® tape (Beiersdorf AG, Hamburg, Germany) along the median line of the lower back feathers to minimize drag70 and facilitate rapid deployment and easy removal upon recapture71. After a single foraging trip, each bird was recaptured in its nest box and the logger and tape were removed. All birds were weighed before and after logger attachment. Fieldwork was approved by the Phillip Island Animal Experimentation Ethics Committee (2.2010) and the Department of Sustainability and Environment of Victoria, Australia (number 10006148).
Frequency-based dive parameters
We first characterized dive sequences during each foraging trip with commonly-used summary statistics, including: (1) trip length; (2) mean dive duration; (3) mean dive depth; and, (4) total dive time, i.e. total time spent below the surface during a trip. After recovery, data were downloaded from the loggers and analysed using custom-written programs in IGOR Pro, version 6.22A (Wavemetrics, Portland, Oregon). We consider diving to have occurred only when the depth at a given sampling interval was greater than 1 m. We include Pearson correlation tests to examine relationships between these parameters.
Fractal analyses
We applied 4 methods to estimate the scaling behaviour of observed dive sequences. We emphasize Detrended Fluctuation Analysis or DFA2 because it has become a mainstream method for examining scaling behaviour in time series data and remains the only method used to examine binary sequences of animal behaviour, though it is not without its critics72. For comparison, we used two variants of DFA (see below), but also two other measures in the Hurst Absolute Value (HAV) method73,74 and the box-counting method75. We performed DFA and HAV using the package ‘fractal’76 and box-counting with the package ‘fractaldim’77, in R statistical software v.2.15.078.
Signal class
A critical first step in examining fractal structure in any data set for which the signal class is not a priori known is to determine whether the sequences reflect fractional Gaussian noise (fGn) or fractional Brownian motion (fBm). Choosing an appropriate scaling exponent estimator and correctly interpreting the results require knowledge about the class of the original signal30,31,41. We therefore tested the signal class of these sequences to determine whether they reflect fGn or fBm by examining the scaling exponent calculated by DFA (αDFA), with αDFA ∈ (0,1) indicating fGn and αDFA ∈ (1,2) indicating fBm.
Detrended fluctuation analysis (DFA)
DFA is a robust method used to estimate the Hurst exponent79,80, i.e. the degree to which time series are long-range dependent and self-affine30,73. The method is described in9 and its application to binary sequences of animal behaviour can be found in16,18,27. Other names for this method include linear detrended scaled windowed variance30 and residuals of regression73. The following description of DFA is taken from the above studies.
First, we coded dive sequences as binary time series [z(i)] in wave form containing diving (denoted by 1) and lags between diving events (denoted by −1) at 1 s intervals to length N. Diving behaviour was recorded at all t during which the subject was submerged to a depth greater than 1 m. Series were then integrated (cumulatively summed) such that

where y(t) is the integrated time series.
After integration, sequences were divided into non-overlapping boxes of length n, a least-squares regression line was fit to the data in each box to remove local linear trends (ŷn(t)) and this process was repeated over all box sizes such that

where F(n) is the average fluctuation of the modified root-mean-square equation across all scales (22, 23, … 2n). The relationship between F and n is of the form

where α is the slope of the line on a double logarithmic plot of average fluctuation as a function of scale. Like all estimators of the Hurst exponent, αDFA = 0.5 indicates a non-correlated, random sequence (white noise), αDFA <0.5 indicates negative autocorrelation (anti-persistent long-range dependence) and αDFA >0.5 indicates positive autocorrelation (persistent long-range dependence)9. Theoretically, αDFA is inversely related to the fractal dimension, a classical index of structural complexity81 and thus smaller values reflect greater complexity (see Theoretical Relationships between Scaling Exponents below).
In addition to the standard (linear) form of DFA, we also used a bridge detrending method in our analysis, which is reportedly more appropriate to fBm signals49 and sequences of lengths greater than 21230. Bridge-detrended Fluctuation Analysis (hereafter DFAb) differs in two distinct ways from the linear form. Bridge-detrended Fluctuation Analysis (hereafter DFAb) differs in two distinct ways from the linear form. First, rather than using the regression line that best fits all data points in each window to detrend the sequence, the slope of the line bridging only the first and last points in each window is calculated30. Second, since it was suggested to work well with fBm rather than fGn sequences49 and assuming that original binary sequences in this study were of the class fGn, we first integrated our time series before applying DFAb, meaning that observed sequences were integrated twice during application of DFAb but only once during DFA. We refer to the scaling exponent generated by this analysis as αDFAb.
Hurst absolute value method (HAV)
We calculated the Hurst exponent H directly using the Absolute Value method. While fractal dimension estimates theoretically provide information about both memory and self-similarity or self-affinity, a previous study has shown that DFA, while giving robust estimates of long-range dependence (serial correlation), fails to capture the self-similarity parameter in data with certain non-Gaussian distributional characteristics74. The same study showed that the absolute value method, on the other hand, captured both parameters. Using this method, time series of length N are divided into smaller windows of length m and the first absolute moment is calculated as

where X(m) is a window of length m and 〈X〉 is the mean of the entire series. The variance δ scales with the window size m as

where HAV is the scaling (absolute value) exponent. Note that while DFA first integrates the time series before calculation, HAV is calculated from the original time series, which in this case is the binary sequence of dives and their lags.
Box-counting dimension
We also employ a classical measure of fractal dimension to measure sequence complexity; box-counting75,82. The principle behind box-counting is simple. First, the integrated curve of the time series is placed within a single box, which is subsequently divided into smaller and smaller equally-sized boxes of size n. We use the entire range of scales from total sequence length down to the resolution of the data (i.e. 1 s). At each value of n, the number of boxes required to cover the curve is counted, with the expected relationship

where n is the box size, N(n) represents the number of boxes required to cover the curve at each box size, k is a constant and Db is the box-counting dimension, which is estimated from the slope of the least squares regression line on the log-log plot of N(n) as a function of n.
Validation of scaling region
We use various methods to ensure the validity of our DFA results. There are algorithmic reasons why values diverge from scaling at small and large scales in a given analysis and some of these are specific to the method used. For example, omitting some of the smallest and largest scales from the analysis is recommended when using DFA and DFAb; excluding the largest scales can reduce variance but increase bias, whereas excluding the smallest scales reduces bias but increases variance30. The range of scales used should therefore be selected to maximize the fit of the regression line, i.e. minimize the mean squared error, on the double logarithmic plot30. Similarly, excluding scales smaller than 1/5 of the total sequence length as well as the two largest scales is recommend when using box-counting75. Alternatively, multiple scaling regions may also exist for biological reasons as a response of an organism to temporal or spatial scale34,36,37,38. Therefore, we independently determined the appropriate range(s) of scales within which strong scaling behaviour existed in our observed sequences using two procedures described in detail in35.
The R2 – SSR procedure involves the creation of a series of regression windows in which the number of data points (scales) ranges from a minimum of 5 (for valid regression analysis) to the maximum number of scales examined, 14 in our case. Each window was then slid across the entire data set so that the smallest windows provided 8 regression estimates, the next window size 7 and so on until only a single regression was performed on the largest window covering all scales. For fractal sequences, there should be a point at which, on a plot of the coefficient of variation (R2) versus the sum of squared residuals (SSR), points converge to maximize the former and minimize the latter. This allows for the identification of the best scaling regions to be used in the calculation of scaling exponents in observed sequences. We performed this analysis on the mean values of F(n) and n across all observed sequences and therefore do not test for variation in scaling regions across individual birds.
The compensated-slope procedure uses a scaling factor c to ‘compensate’ the scaling behaviour such that, in the case of DFA,

where F(n) is the fluctuation about the box size n as described above, c is the compensation exponent taking values of c ∈ (0, 1) for self-affine curves such as those examined here and Df is the fractal dimension estimate for the sequence. By varying c between 0 and 1, we can find the value at which our dimension estimate (based on the range of scales determined via the R2 – SSR procedure) and compensated slope converge to 0 to produce a straight line (if scaling exists) with slope zero on the plot of Log(nc*n−Df) versus Log(n). Here, we used 5 values for c, the lowest (0.70) and highest (1.00) of which for illustrative purposes and the middle three values representing the minimum, best and maximum estimates of αDFA derived from the sliding windows used in the R2 – SSR procedure. We then bootstrapped 1000 simulations to determine whether variation from this zero slope in observed sequences could be explained by noise, i.e. data points fall within the 95% confidence intervals, or whether scaling was simply unlikely given the fractal dimension estimate produced.
While the procedures described above are robust, many previous studies have relied on less convincing measures to support their results, such as high coefficients of variation for the slope of the double logarithmic plot and showing that surrogate sequences in which observed data points have been shuffled to break any serial correlation results in the expected relationship αDFArandom = 0.516,27,46. We also present R2 values in our study and take the mean of 10 surrogate sequences for each observed sequence (i.e. N = 28*10 = 280), but additionally apply the R2 – SSR and compensated-slope procedures to these randomized sequences for comparison with observed sequences. Furthermore, we computed αDFA for simulated random binary sequences of various lengths (211 ~ 216 s) and distributions of diving behaviour (100 simulations for each of 5 binary probability distributions, i.e. diving versus its lag, at 0.25, 0.33, 0.50, 0.66 and 0.75) for comparison with observed and surrogate data. The results of these analyses are presented as Supplementary Information online.
Finally, in addition to the original 1 s interval sequences, we also applied the linear form of DFA to sequences sampled at 5, 10, 20 and 30 s intervals to determine whether the same scaling relationship would hold given different data resolutions. We also applied the R2 – SSR and compensated-slope procedures to these sequences to determine whether their scaling regions corresponded to those in the high-resolution 1 s interval sequences.
Theoretical relationships between scaling exponents
Most scaling exponents and other fractal dimension estimates are theoretically related. For example, αDFA provides a robust estimate of the Hurst exponent H30,73, such that
for fGn: H = αDFA
for fBm: H = αDFA − 1
In addition, H itself is inversely related to fractal dimension, here the box-counting dimension, such that for one-dimensional time series like those examined here

While these measures are theoretically related, in practice the various methods often lead to different results, either because of mathematical differences or non-linearity in the series themselves73,83,84. Therefore, we estimated each of these parameters separately using the methods described above for a more robust interpretation of the results. We include an analysis of Pearson correlation coefficients to test for agreement between the four measures used.
Statistical analyses
Using the scaling exponents estimated via the above methods as Gaussian-distributed response variables (X2 goodness-of-fit tests, P>0.05), we constructed general linear mixed-effects (LME) models to determine whether age, sex, initial body mass and the age of the young chicks being guarded were associated with variation in penguin dive sequence complexity (N = 28). We could not use final body mass to calculate mass gain during trips because measurements were taken hours after birds had returned to the nest and had already fed their chicks. We used the same approach to test whether these individual factors could explain variance observed in the summary statistics for each foraging trip, which were also Gaussian-distributed across individuals (X2 goodness-of-fit tests, P>0.05). For all models, we set the date on which data were collected for each individual as a random factor in our analyses to control for temporal variation. All LME models were run using the nlme package85 in R. Models were fit by restricted maximum likelihood, using all factors and covariates in a single full model to estimate the parameter effects. Finally, we used a general linear model (GLM) to test whether the summary statistics themselves could explain variation in the observed scaling exponents. In all models, we tested for variance inflation caused by correlation between fixed effects using the car package in R86. If the variance inflation factor exceeded 10, we arbitrarily removed one of the 2 correlated variables and ran the model again. We set the alpha level for all statistical analyses at 0.05.
References
Havlin, S. et al. Scaling in nature: from DNA through heartbeats to weather. Physica A -Statistical Mechanics and Its Applications 273, 46–69 (1999).
Peng, C. K. et al. Long-range correlations in nucleotide sequences. Nature 356, 168–170 (1992).
Stanley, H. E. et al. Scaling and universality in animate and inanimate systems. Physica A -Statistical Mechanics and Its Applications 231, 20–48 (1996).
Goldberger, A. L., Rigney, D. R. & West, B. J. Chaos and fractals in human physiology. Sci. Am. 262, 43–49 (1990).
Peng, C. K. et al. Quantifying fractal dynamics of human respiration: age and gender effects. Ann. Biomed. Eng. 30, 683–692 (2002).
West, B. J. & Goldberger, A. L. Physiology in fractal dimensions. Am. Sci. 75, 354–365 (1987).
Mandelbrot, B. B. How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science 156, 636–638 (1967).
Glenny, R. W., Robertson, H. T., Yamashiro, S. & Bassingthwaighte, J. B. Applications of fractal analysis to physiology. J. Appl. Physiol. 70, 2351–2367 (1991).
Peng, C. K., Havlin, S., Stanley, H. E. & Goldberger, A. L. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time-series. Chaos 5, 82–87 (1995).
Nelson, T. R., West, B. J. & Goldberger, A. L. The fractal lung: universal and species-related scaling patterns. Experientia 46, 251–254 (1990).
Shlesinger, M. F. & West, B. J. Complex fractal dimension of the bronchial tree. Phys. Rev. Lett. 67, 2106–2108 (1991).
Viswanathan, G. M., Da Luz, M. G. E., Raposo, E. P. & Stanley, H. E. The physics of foraging. (Cambridge University Press, 2011).
Bartumeus, F. Levy processes in animal movement: an evolutionary hypothesis. Fractals 15, 151–162 (2007).
Viswanathan, G. M., Raposo, E. P. & da Luz, M. G. E. Levy flights and superdiffusion in the context of biological encounters and random searches. Physics of Life Reviews 5, 133–150 (2008).
Sims, D. W. et al. Scaling laws of marine predator search behaviour. Nature 451, 1098–1102 (2008).
MacIntosh, A. J., Alados, C. L. & Huffman, M. A. Fractal analysis of behaviour in a wild primate: behavioural complexity in health and disease. J. Royal Soc. Interface 8, 1497–1509 (2011).
Alados, C. L., Escos, J. M. & Emlen, J. M. Fractal structure of sequential behaviour patterns: an indicator of stress. Anim. Behav. 51, 437–443 (1996).
Alados, C. L. & Weber, D. N. Lead effects on the predictability of reproductive behavior in fathead minnows (Pimephales promelas): a mathematical model. Environ. Toxicol. Chem. 18, 2392–2399 (1999).
Motohashi, Y., Miyazaki, Y. & Takano, T. Assessment of behavioral effects of tetrachloroethylene using a set of time series analyses. Neurotoxicol. Teratol. 15, 3–10 (1993).
Rutherford, K. M. D., Haskell, M. J., Glasbey, C. & Lawrence, A. B. The responses of growing pigs to a chronic-intermittent stress treatment. Physiol. Behav. 89, 670–680 (2006).
Seuront, L. & Cribb, N. Fractal analysis reveals pernicious stress levels related to boat presence and type in the Indo-Pacific bottlenose dolphin, Tursiops aduncus. Physica A -Statistical Mechanics and Its Applications 390, 2333–2339 (2011).
West, B. J. Physiology in fractal dimensions: error tolerance. Ann. Biomed. Eng. 18, 135–149 (1990).
Goldberger, A. L. Fractal variability versus pathologic periodicity: complexity loss and stereotypy in disease. Perspect. Biol. Med. 40, 543–561 (1997).
Shimada, I., Kawazoe, Y. & Hara, H. A temporal model of animal behavior based on a fractality in the feeding of Drosophila melanogaster. Biol. Cybern. 68, 477–481 (1993).
Shimada, I., Minesaki, Y. & Hara, H. Temporal fractal in the feeding behavior of Drosophila melanogaster. J. Ethol. 13, 153–158 (1995).
Cole, B. J. Fractal time in animal behavior: the movement activity of Drosophila. Anim. Behav. 50, 1317–1324 (1995).
Alados, C. L. & Huffman, M. A. Fractal long-range correlations in behavioural sequences of wild chimpanzees: a non-invasive analytical tool for the evaluation of health. Ethology 106, 105–116 (2000).
Delignieres, D. et al. Fractal analyses for ‘short’ time series: A re-assessment of classical methods. J. Math. Psychol. 50, 525–544 (2006).
Weron, R. Estimating long-range dependence: finite sample properties and confidence intervals. Physica A -Statistical Mechanics and Its Applications 312, 285–299 (2002).
Cannon, M. J., Percival, D. B., Caccia, D. C., Raymond, G. M. & Bassingthwaighte, J. B. Evaluating scaled windowed variance methods for estimating the Hurst coefficient of time series. Physica A: Statistical Mechanics and its Applications 241, 606–626 (1997).
Eke, A. et al. Physiological time series: distinguishing fractal noises from motions. Pflugers Archiv-European Journal of Physiology 439, 403–415 (2000).
Maraun, D., Rust, H. W. & Timmer, J. Tempting long-memory - on the interpretation of DFA results. Nonlinear Processes in Geophysics 11, 495–503 (2004).
Beran, J. Statistics for long-memory processes. (Chapman and Hall/CRC, 1994).
Seuront, L., Brewer, M. & Strickler, J. R. in Handbook of scaling methods in aquatic ecology ((eds Seuront, L. & Strutton, P. G.) 333–359 (CRC Press, 2004).
Seuront, L. Fractals and multifractals in ecology and aquatic science. 344 (Taylor and Francis, LLC, 2010).
Wiens, J. A., Crist, T. O., With, K. A. & Milne, B. T. Fractal patterns of insect movement in microlandscape mosaics. Ecology 76, 663–666 (1995).
Nams, V. O. Using animal movement paths to measure response to spatial scale. Oecologia 143, 179–188 (2005).
Nams, V. O. & Bourgeois, M. Fractal analysis measures habitat use at different spatial scales: an example with American marten. Can. J. Zool. 82, 1738–1747 (2005).
Garcia, F., Carrere, P., Soussana, J. F. & Baumont, R. Characterisation by fractal analysis of foraging paths of ewes grazing heterogeneous swards. Appl. Anim. Behav. Sci. 93, 19–37 (2005).
Clauset, A., Shalizi, C. & Newman, M. Power-Law Distributions in Empirical Data. SIAM Review 51, 661–703 (2009).
Delignieres, D., Torre, K. & Lemoine, L. Methodological issues in the application of monofractal analyses in psychological and behavioral research. Nonlinera Dynamics, Psychology and Life Sciences 9, 451–477 (2005).
Boyd, I. L., Kato, A. & Ropert-Coudert, Y. Bio-logging science: sensing beyond the boundaries. Memoirs of the National Institute of Polar Research 58, 1–14 (2004).
Ropert-Coudert, Y. & Wilson, R. P. Trends and perspectives in animal-attached remote sensing. Frontiers in Ecology and the Environment 3, 437–444 (2005).
Ropert-Coudert, Y., Kato, A., Gremillet, D. & Crenner, F. in Sensors for Ecology: Towards integrated knowledge of ecosystems ((eds LeGalliard, J. F., Guarini, J. M. & Gaill, F.) 17–41 (Centre National de la Recherche Scientifique (CNRS), Institut Écologie et Environnement (INEE) 2012).
Kembro, J. M., Marin, R. H., Zygaldo, J. A. & Gleiser, R. M. Effects of the essential oils of Lippia turbinata and Lippia polystacha (Verbenaceae) on the temporal pattern of locomotion of the mosquito Culex quinquefasciatus (Diptera: Culicidae) larvae. Parasitol. Res. 104, 1119–1127 (2009).
Kembro, J. M., Perillo, M. A., Pury, P. A., Satterlee, D. G. & Marin, R. H. Fractal analysis of the ambulation pattern of Japanese quail. Br. Poult. Sci. 50, 161–170 (2009).
Rutherford, K. M. D., Haskell, M. J., Glasbey, C., Jones, R. B. & Lawrence, A. B. Fractal analysis of animal behaviour as an indicator of animal welfare. Anim. Welf. 13, S99–S103 (2004).
Gao, J. B. et al. Assessment of long-range correlation in time series: How to avoid pitfalls. Physical Review E 73, (2006).
Stroe-Kunold, E., Stadnytska, T., Werner, J. & Braun, S. Estimating long-range dependence in time series: An evaluation of estimators implemented in R. Behav. Res. Methods 41, 909–923 (2009).
Humphries, N. E. et al. Environmental context explains Lévy and Brownian movement patterns of marine predators. Nature 465, 1066–1069 (2010).
Sims, D. W., Humphries, N. E., Bradford, R. W. & Bruce, B. D. Lévy flight and Brownian search patterns of a free-ranging predator reflect different prey field characteristics. J. Anim. Ecol. 81, 432–442 (2012).
Rutherford, K. M. D., Haskell, M. J., Glasbey, C., Jones, R. B. & Lawrence, A. B. Detrended fluctuation analysis of behavioural responses to mild acute stressors in domestic hens. Appl. Anim. Behav. Sci. 83, 125–139 (2003).
Houston, A. I. & Carbone, C. The optimal llocation of time during the dive cycle. Behav. Ecol. 3, 233–262 (1992).
Kooyman, G. L. Diverse divers: physiology and behavior. (Springer-Verlag, 1989).
Reynolds, A. M. On the origin of bursts and heavy tails in animal dynamics. Physica A -Statistical Mechanics and Its Applications 390, 245–249 (2011).
Bartumeus, F. Behavioral intermittence, Levy patterns and randomness in animal movement. Oikos 118, 488–494 (2009).
Kramer, D. L. Thebehavioral ecology of air breathing by aquatic animals. Can. J. Zool. 66, 89–94 (1988).
Seuront, L. & Leterme, S. Increased zooplankton behavioral stress in response to short-term exposure to hydrocarbon contamination. The Open Oceanography Journal 1, 1–7 (2007).
Turchin, P. Fractal analyses of animal movement: A Critique. Ecology 77, 2086–2090 (1996).
Benhamou, S. How to reliably estimate the tortuosity of an animal's path:: straightness, sinuosity, or fractal dimension? J. Theor. Biol. 229, 209–220 (2004).
Fritz, H., Said, S. & Weimerskirch, H. Scale–dependent hierarchical adjustments of movement patterns in a long–range foraging seabird. Proc. R. Soc. Lond. B Biol. Sci. 270, (2003).
Mori, Y. Dive bout organization in the chinstrap penguin at seal island, Antarctica. J. Ethol. 15, 9–15 (1997).
Hart, T., Coulson, T. & Trathan, P. N. Time series analysis of biologging data: autocorrelation reveals periodicity of diving behaviour in macaroni penguins. Anim. Behav. 79, 845–855 (2010).
Ropert-Coudert, Y., Kato, A., Naito, Y. & Cannell, B. L. Individual diving strategies in the Little Penguin. Waterbirds 26, 403–408 (2003).
Le Vaillant, M. et al. How age and sex drive the foraging behaviour in the king penguin. Marine Biology 160, 1147–1156 (2013).
Kato, A., Ropert-Coudert, Y. & Chiaradia, A. Regulation of trip duration by an inshore forager, the little penguin (Eudyptula Minor), during incubation. The Auk 125, 588–593 (2008).
Zimmer, I., Ropert-Coudert, Y., Poulin, N., Kato, A. & Chiaradia, A. Evaluating the relative importance of intrinsic and extrinsic factors on the foraging activity of top predators: a case study on female little penguins. Marine Biology 158, 715–722 (2011).
Chiaradia, A. & Kerry, K. R. Daily nest attendance and breeding performance in the Little Penguin Eudyptula minor at Phillip Island, Australia. Mar. Ornithol. 27, 13–20 (1999).
Arnould, J. P., Dann, P. & Cullen, J. M. Determining the sex of little penguins (Eudyptula minor) in northern Bass Strait using morphometric measurements. Emu 104, 261–265 (2004).
Bannasch, D. G., Wilson, R. P. & Culik, B. Hydrodynamic aspects of design and attachment of a back-mounted device in penguins. J. Theor. Biol. 194, 83–96 (1994).
Wilson, R. P. et al. Long term attachment of transmitting and recording devices to penguins and other seabirds. Wildl. Soc. Bull. 25, 101–106 (1997).
Bryce, R. M. & Sprague, K. B. Revisiting detrended fluctuation analysis. Sci. Rep. 2 (2012).
Taqqu, M. S., Teverovsky, V. & Willinger, W. Estimators for long-range dependence: an empirical study. Fractals 3, 785–788 (1995).
Mercik, S., Weron, K., Burnecki, K. & Weron, A. Enigma of self-similarity of fractional Levy stable motions. Acta Physica Polonica B 34, 3773–3791 (2003).
Liebovitch, L. S. & Toth, T. A fast algorithm to determine fractal dimensions by box counting. Phys. Lett. A 141, 386–390 (1989).
Constantine, W. & Percival, D. fractal: fractal time series modeling and analysis. R package version 1.1-1, <http://CRAN.R-project.org/package=fractal> (2011).
Sevcikova, H., Gneiting, T. & Percival, D. fractaldim: estimation of fractal dimensions. R package version 0.8-1, <http://CRAN.R-project.org/package=fractaldim> (2011).
R: a language and environment for statistical computing. v.2.15.0. (R Foundation for Statistical Computing, Vienna, Austria, 2012).
Hurst, H. E. Long-term storage capacity of reservoirs. Transactions of the American Society of Civil Engineers 116, 770–808 (1951).
Mandelbrot, B. B. & Van Ness, J. W. Fractional brownian motions, fractional noises and applications. SIAM Review 10, 422–437 (1968).
Mandelbrot, B. B. The fractal geometry of nature. (W. H. Freeman and Company, 1983).
Longley, P. A. & Batty, M. On the Fractal Measurement of Geographical Boundaries. Geographical Analysis 21, 47–67 (1989).
Rea, W., Oxley, L., Reale, M. & Brown, J. Estimators for long range dependence: an empirical study. (2009).<http://arxiv.org/abs/0901.0762>.
Gneiting, T. & Schlather, M. Stochastic models that separate fractal dimension and the Hurst effect. Society for Industrial and Applied Mathematics 46, 269–282 (2004).
Pinheiro, J., Bates, D., DebRoy, S. & Sarkar, D. nlme: Linear and Nonlinear Mixed Effects Models. R package version 3.1-98, <http://CRAN.R-project.org/package=nlme> (2011).
Fox, J. & Weisberg, S. An R companion to applied regression Second Edition edn, (Sage, 2011).
Acknowledgements
We thank Concepción Alados for her constructive comments on earlier versions of this manuscript. We also thank Phillip Island Nature Parks for their continued support, in particular Peter Dann, Marcus Salton, Leanne Renwick and Paula Wasiak. The Australian Academy of Science has been a great supporter to this collaborative work. AM was financially supported by the Japan Society for the Promotion of Science through its (1) Research Exchange Grant and (2) Core-to-Core Program AS-HOPE project administered by the Kyoto University Primate Research Institute. LP was supported by grants from the CNRS and Régiond'Alsace. This study was further supported in part by the French National Research Agency (ANR-2010-BLAN-1728-01, Picasso).
Author information
Authors and Affiliations
Contributions
A.M., Y.R.-C. and A.K. conceived of the experiment. L.P. collected the data and analysed the frequency-based measures presented. A.C. managed the field site and data collection. A.K. analysed and converted the raw data from the loggers and arranged the data set. A.M. conducted all fractal analyses and wrote the manuscript. All authors contributed to manuscript discussion and revision.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
MacIntosh, A., Pelletier, L., Chiaradia, A. et al. Temporal fractals in seabird foraging behaviour: diving through the scales of time. Sci Rep 3, 1884 (2013). https://doi.org/10.1038/srep01884
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01884
This article is cited by
-
The relevance of a right scale for sampling when studying high-resolution behavioral dynamics
Scientific Reports (2023)
-
Aggressive dominance can decrease behavioral complexity on subordinates through synchronization of locomotor activities
Communications Biology (2019)
-
The fractal organization of ultradian rhythms in avian behavior
Scientific Reports (2017)
-
Shallow divers, deep waters and the rise of behavioural stochasticity
Marine Biology (2017)
-
Optimal search patterns in honeybee orientation flights are robust against emerging infectious diseases
Scientific Reports (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.