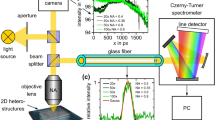
Abstract
The Raman scattering of single- and few-layered WS2 is studied as a function of the number of S-W-S layers and the excitation wavelength in the visible range (488, 514 and 647 nm). For the three excitation wavelengths used in this study, the frequency of the A1g(Γ) phonon mode monotonically decreases with the number of layers. For single-layer WS2, the 514.5 nm laser excitation generates a second-order Raman resonance involving the longitudinal acoustic mode (LA(M)). This resonance results from a coupling between the electronic band structure and lattice vibrations. First-principles calculations were used to determine the electronic and phonon band structures of single-layer and bulk WS2. The reduced intensity of the 2LA mode was then computed, as a function of the laser wavelength, from the fourth-order Fermi golden rule. Our observations establish an unambiguous and nondestructive Raman fingerprint for identifying single- and few-layered WS2 films.
Similar content being viewed by others
Introduction
Individual monolayers of transition metal dichalcogenides such as MoS2 and WS2 have recently caught the attention of the scientific community because these 2-dimensional semiconductors could have properties more attractive for specific applications than those of graphene1,2 and boron nitride3,4. A single layer of MX2 [M = (Mo or W) and X = (S, Se or Te)] typically contains one atomic layer of metal atoms with 6-fold in-plane coordination, hexagonally packed between two trigonal atomic layers of chalcogenide atoms. In single-layer form, the absence of interlayer coupling plus the lack of inversion symmetry (for supported films) leads to optical and electronic properties that differ markedly from those of the bulk5,6,7,8,9. For example, the electronic band structure transitions from an indirect gap (in the bulk) to a direct gap in the monolayer7 and valley polarization (i.e. “valleytronics”) can be induced in monolayer MoS2 by circularly polarized light10,11. While MoS2 has received copious attention in the search for new properties and potential applications of 2D semiconductors8,9,12,13,14,15,16,17,18,19, little attention has been paid to monolayer and few-layer WS2. In this respect, we have recently demonstrated the synthesis of single-layer WS2 triangular islands and observed intense room-temperature photoluminescence (PL) associated with specific edges20. Although Raman spectroscopy has become a very powerful tool for studying graphene21,22,23 and MoS213,17,18,19,24,25, the Raman scattering of single- and few-layered WS2 still remains largely unexplored. Raman spectroscopy can not only be used to identify the number of layers13,21,22,25,26, but also probe subtle details in the electronic band structure and phonon dispersion through resonant Raman scattering21,27. Here we provide the first systematic study of the Raman response in monolayer and few-layer WS2 as a function of the laser excitation wavelength. We report a novel resonant second-order Raman feature in single-layered WS2 and discuss the general characteristics of the phonon modes that can provide a fingerprint for monolayer WS2.
Results
As previously reported20, the synthesis of single- and few-layered WS2 triangular 2D islands follows a two-step approach of thermal evaporation of tungsten trioxide (WO3) followed by sulfurization (see Methods section). The sample morphology, crystal structure and chemical composition were studied by means of scanning and transmission electron microscopy (SEM, TEM) (Figures 1a–c)20. Electron diffraction (inset in Figure 1b) reveals large single crystal domains with a high degree of crystallinity. Atomic force microscopy (AFM) was used to determine the number of layers within these WS2 triangular islands (Figures 1d). We extracted the thickness and wavelength-dependent behavior of the lattice vibrations in these 2D islands by correlating AFM images with Raman spectroscopy maps.
(a) SEM image of a monolayer WS2 triangular island.(b) TEM image of a WS2 island transferred to a lacey carbon grid with inset showing the electron diffraction pattern of the entire region. (c) High-resolution phase-contrast TEM image showing the hexagonal arrangement of the WS2 structure with inset showing the Fourier transform of the micrograph. (d) AFM image of a WS2 island and the corresponding height profile along the dashed line. (e) and (f) Room-temperature Raman spectra from a monolayer WS2 region, using the 514.5 and 488 nm laser excitation, respectively, including Lorentzian peak fits for 514.5 nm data. The inset in (f) shows the atomic displacements for the in-plane phonon mode E12g(Γ) and the out-of-plane phonon mode A1g(Γ) for two adjacent layers, the dashed line represents the weak inter-layer van der waals interaction.
Raman spectra for bulk (i.e. multi-layered) WS2 and MoS2 have been previously studied. In a backscattering geometry, these spectra include first-order modes at the Brillouin zone center (E12g(Γ) and A1g(Γ)) plus a zone-edge mode – activated by disorder – which has been identified as the longitudinal acoustic mode at the M point, LA(M). The longitudinal acoustic phonons LA(M) are in-plane collective movements of the atoms in the lattice, similar to the sound waves. They are periodic compressions and expansions of the lattice that occur along the direction of propagation. The symbol (M) refers to the specific direction and magnitude of the momentum q of the phonon; in the phonon dispersion (frequency vs. momentum), they appear at the M-point of the Brillouin zone. Additional peaks correspond to multi-phonon combinations of these modes28,29,30. Previous reports on monolayer MoS2 and chemically exfoliated WS214 have focused exclusively on the first-order E12g(Γ) and A1g(Γ) optical modes. Resonant Raman scattering in single-layered dichalcogenides has not previously been observed.
Figures 1e and f show typical Raman spectra of monolayer WS2 regions using 514.5 nm and 488 nm excitations. For λexc = 488 nm, the Raman spectrum is dominated by the first-order modes: LA(M) at 176 cm−1, E12g(Γ) at 356 cm−1 and A1g(Γ) at 418 cm−1. However, when monolayer WS2 is excited at 514.5 nm, the Raman spectrum becomes very rich, revealing many second-order peaks that are stronger than those observed in the bulk material. Figures 1e and 1f give symmetry assignments for several peaks according to previous reports in bulk and fullerene-like WS2 nanostructures. For λexc = 514 nm, it is remarkable that the intensity of the strongest second-order Raman peak, the 2LA(M) mode at 352 cm−1, is approximately twice the intensity of the first-order A1g(Γ). Although the 2LA(M) mode overlaps with the first-order E12g(Γ) mode at 356 cm−1, the multi-peak Lorentzian fitting shown in Figure 1e clearly separates their individual contributions.
The samples contain a large number of monolayer islands (1L), plus enough multilayer islands (see Figure 2a) to study the thickness dependence of the Raman response. The AFM height profile shown in Figure 2e confirms the presence of one and few-layered regions within a single island. Raman mapping of this island at λexc = 514 nm provides spatial maps of the 2LA(M) intensity and the A1g(Γ) mode frequency and intensity, as shown in Figures 2b,c,d. The absolute intensity of the 2LA(M) mode increases with decreasing the number of layers, while the intensity of the A1g(Γ) displays the opposite behavior. The softening of the A1g(Γ) mode with decreasing number of layers (depicted in Figures 2c, e) presumably results from weaker interlayer contributions to the phonon restoring forces.
(a) AFM image of a WS2 triangular island, which varies from four to one layers thick.Also Raman mappings of the same WS2 island (using 514.5 nm laser excitation): (b) intensity of the 2LA second-order mode, (c) frequency and (d) intensity of the A1g mode. (e) Line profiles along the red horizontal line in each image corresponding to height, 2LA intensity, A1g intensity and A1g peak position (ω). The Raman mappings as well as the intensity profiles refer to the maximum intensity of the peaks (not the integrated intensities).
Figure 3 summarizes the WS2 Raman spectra as a function of island thickness and excitation wavelength. For λexc = 647 nm, the absolute intensity of all Raman modes increases with the number of layers, which suggests that at this wavelength the Raman intensity is mainly affected by the scattering volume. A baseline related to the low-energy tail of the photoluminescence (which is centered around 630 nm20) appears for 3L and becomes more obvious in thinner samples. As reported in a previous work20, room-temperature PL is associated with a transition from indirect-gap few-layer WS2 to direct-gap monolayer WS2. Raman spectra taken with λexc = 488 nm also showed an increase in the absolute intensity from 1L to 3L. However, the intensities for bulk are lower than for the 1L case. Such a behavior has been previously observed in graphene31 and MoS213 deposited on SiO2/Si substrates and is mainly attributed to optical interference in both the excitation laser and the Raman signal emitted by the sample. In contrast to these relatively familiar behaviors, the response at λexc = 514.5 nm is a special case: the second-order Raman peaks, in particular the 2LA(M) mode, increase in intensity with decreasing number of layers and reach a maximum for the monolayer.
Raman spectra collected from regions with different WS2 thicknesses (1L, 2L 3L and bulk) using three different excitation wavelengths: (a) 488 nm, (b) 514.5 nm and (c) 647 nm.
For each individual wavelength all the spectra, including that from the bulk, were acquired using the same experimental conditions of laser power and collection time.
We performed multi-peak Lorentzian fittings on each spectrum to obtain the thickness-dependent frequency of the main WS2 Raman peaks (2LA(M), E12g(Γ) and A1g(Γ)) for each wavelength, as shown in Figure 4a. The A1g(Γ) mode blueshifts when increasing the number of WS2 layers. This hardening of the A1g mode is consistent with the increasing restoring force caused by van der Waals interactions established among layers and it is in agreement with previous results reported for MoS218. The E12g(Γ) and 2LA(M) phonon modes, however, exhibit very subtle redshifts when increasing the number of layers. It is worth noticing that in WS2, the close proximity of the 2LA(M) and E12g(Γ) increases the error in determining the frequency shift of both modes. The change in frequency is of the order of magnitude of the error bar, which is also affected by the fitting process, thus making more difficult to establish a clear frequency dependence with the number of layers. An anomalous behavior of the E12g(Γ) mode has been previously reported in few-layered MoS2 films13,18,24 and it might be caused by a stronger dielectric screening of the long-range Coulomb interactions between the effective charges in thicker samples25. A change in dielectric screening with the number of layers is also expected for WS2.
Intensity ratios and peak frequencies of WS2 Raman modes.
(a) Frequencies of the A1g,  , and 2LA Raman modes as a function of thickness (number of WS2 monolayers) for the three excitation laser lines. Each point represents an average over ten different positions and the error bars correspond to the standard deviations (b) Thickness-dependent intensity ratios of
, and 2LA Raman modes as a function of thickness (number of WS2 monolayers) for the three excitation laser lines. Each point represents an average over ten different positions and the error bars correspond to the standard deviations (b) Thickness-dependent intensity ratios of  (for λexc = 514.5 nm) and
(for λexc = 514.5 nm) and  (for λexc = 488 and 647 nm).
(for λexc = 488 and 647 nm).
We also studied the relative intensities of the strongest Raman peaks for each λexc as a function of the number of layers, as shown in Figure 4b. For λexc = 488 nm and λexc = 647 nm, the most intense features in the Raman spectrum correspond to the E12g(Γ) and A1g(Γ) modes and the intensity ratio  does not show major changes with the number of layers. The most interesting scenario again occurs for λexc = 514.5 nm. In this case, the strongest Raman peaks are those associated with the 2LA(M) and A1g(Γ) phonon modes. The relative intensity
does not show major changes with the number of layers. The most interesting scenario again occurs for λexc = 514.5 nm. In this case, the strongest Raman peaks are those associated with the 2LA(M) and A1g(Γ) phonon modes. The relative intensity  increases dramatically for double- and single-layered films. We have repeated the experiment in different regions of the samples and also in WS2 films suspended on a TEM grid; the ratio
increases dramatically for double- and single-layered films. We have repeated the experiment in different regions of the samples and also in WS2 films suspended on a TEM grid; the ratio  is always larger than 2 only for monolayer films; thus it provides an accurate fingerprint for monolayer WS2. We attribute the intense 2LA signal in monolayer WS2 at λexc = 514.5 nm to a double-resonant (DR) Raman process which is possible only in the specific electronic band structure of the monolayer, as described below.
is always larger than 2 only for monolayer films; thus it provides an accurate fingerprint for monolayer WS2. We attribute the intense 2LA signal in monolayer WS2 at λexc = 514.5 nm to a double-resonant (DR) Raman process which is possible only in the specific electronic band structure of the monolayer, as described below.
Table 1 summarizes the frequency for the main Raman modes as well as the intensity ratio for the most intense peaks, as a function of the number of layers and the excitation wavelength.
Discussion
Figure 5 shows the phonon dispersion and electronic band structures for bulk and monolayer WS2, obtained using the density functional perturbation theory in the local density approximation. The experimental Raman peak at 176 cm−1 falls in the range of the calculated zone-edge acoustic phonons. This mode has been identified with the longitudinal acoustic mode around the M point of the Brillouin zone28,30 , although an alternative identification with the K point has been proposed by at least one group29. This finite-wavevector mode is presumably activated by disorder to become Raman active28. The precise doubling of frequency for the peak at 352 cm−1 strongly suggests that such a peak is a second-order mode originated from the same phonon. The unique sensitivity of second-order resonant Raman processes to precise phonon wavevectors enables us to unambiguously identify the second-order 352 cm−1 peak (and by extension, the first-order 176 cm−1 peak) with the M-point LA phonon, as described below.
Phonon dispersion plus density of states [left]; and electronic band structures [right] for WS2 monolayer [top] and bulk [bottom], respectively.
The electronic band structure in (b) was calculated by LDA with 1.94 eV band gap; the dashed line corresponds to the bottom of the conduction band with a rigid shift to match the experimental 2.1 eV band gap. Although the phonon dispersions for monolayer and bulk are very similar, their band structures are clearly different. While the direct gap at the K point remains almost the same; the electronic bands between Γ-M and Γ-K undergo major changes associated with the indirect-to-direct bandgap transition from bulk to monolayer. The horizontal dashed lines in (b) and (d) are guides for the eye to visualize better these differences.
The double resonant Raman process involves two phonons with equal and opposite momentum and an intermediate excited electronic state that resonates with the electronic band structure (in addition to the resonance for the initial optical transition, hence the term double resonance). For a second-order Raman process to satisfy the requirements for double resonance, the optical excitation energy must match a vertical electronic transition (vertical black arrows in Figure 6) and the conduction band must contain quasi-isoenergetic electronic states (dashed red arrows in Figure 6) at a momentum difference corresponding to the phonon momentum ±q (or similarly for the valence band in the case of phonon-hole scattering). The momentum dependence of the electronic structure and phonon dispersion must combine to produce sharp peaks in momentum space for the double resonant process, in order to produce a sharp Raman feature.
Schematic of the double-resonant Raman process that generates the 2LA(M) experimental peak.
Calculated data from the valence (blue) and conduction (red) bands are used for the visualization. An incident photon with energy hνi produces a vertical electronic transition (black vertical arrow) from valence to conduction band. The electron in the conduction band then experiences two electron-phonon scattering events, the first scattering event involving a phonon with momentum +q and the second involving a phonon with momentum –q (red dashed double arrow). Finally another vertical transition from conduction to valence band emits a Raman-shifted photon with energy hνf.
Since the most important structure in the double-resonant process typically arises from the complex interplay of electron and phonon dispersion relations, the essential features of double-resonant Raman processes can be captured in a ‘reduced’ calculation under a simplifying assumption of constant scattering matrix elements for the component scattering events. Thus the ab initio electronic and phonon band structures can be used to compute the reduced intensity of the 2LA mode from the fourth-order Fermi golden rule – for details, see the Methods section. The numerical results corresponding to this model are summarized in Figure 7, where the reduced intensity of the 2LA double resonant mode at different q-points is plotted as a function of the laser wavelength. The reduced intensities for the bulk and the monolayer were investigated in the vicinity of the three laser excitations: 488, 514.5 and 647 nm. At 488 and 647 nm the Raman intensity of the bulk is always greater than the monolayer (not shown). However, the monolayer exhibits a pronounced resonant peak close to 514.7 nm. Furthermore, by restricting the phonon wavevectors allowed in the calculation, it is possible to clearly identify the reciprocal space location of the dominant phonon contributions to the double resonance. In particular, Figure 7 compares the contributions from phonons in the vicinity of K and M; the dominance of the M-point contribution is obvious, which justifies the identification of this process with 2LA(M).
Reduced Raman intensity of the 2LA Raman line at the vicinity of K and M as a function of laser energy using a double-resonant model for both bulk and monolayer WS2 .
Although the reduced intensities were also investigated around 488 and 647 nm (not shown), the monolayer system shows a resonant peak only for the vicinity of 514.7 nm.
In the bulk system, changes in the electronic structure drive the system out of resonance for both electron-phonon and hole-phonon mediated processes. By comparing Figure 5(b) and 5(d) it can be observed that the direct band gap at the K point is similar for both bulk and monolayer WS2. However, the electronic bands between Γ-M and Γ-K exhibit major differences, which reveal an indirect to direct band gap material transformation when the system transitions from bulk to monolayer. This tendency persisted after a small rigid shift of the conduction band was applied to correct the well-known DFT underestimation of the band gap and match the experimental gap of 2.1 eV32, which is similar to the GW-corrected direct gap of 2.1 eV33.
In summary, we have systematically studied the thickness- and wavelength-dependent Raman behavior for newly synthesized single- and few-layered two-dimensional WS2 crystals. Our results reveal that the A1g(Γ) mode softens while the 2LA(M) and E12g(Γ) modes present a very subtle hardening with decreasing number of WS2 layers. The analysis presented here unambiguously confirms that the 176 cm-1 feature arises from an M-point phonon. In addition, a striking increase in the intensity of the 2LA(M) mode occurs with 514 nm laser excitation. This behavior can be explained in terms of a double resonance process which is active only in the monolayer. Both frequency shifts and changes in relative intensity can provide an unambiguous, nondestructive identification of monolayer WS2. The more singular dispersion relations of electrons and phonons in two dimensions (as compared to three) facilitate the generation of sharp Raman features via a complex double-resonant process. This mechanism may be more broadly applicable in characterizing the structural, electronic and vibrational properties of other layered systems.
Methods
Synthesis
WO3 thin films (5–20 Å) were thermally deposited on SiO2/Si substrates in high vacuum (10−5–10−6 Torr). Subsequently, the films were transferred into a quartz tube reactor. During the sulfurization of the WO3 films, samples were kept at 800°C for 30 min under an Argon flow and S vapors were generated from S powders placed up-stream in a lower temperature region (~250°C) which was independently controlled.
For the TEM observations, we transferred as-grown WS2 islands onto gold Quantifoil® TEM grids (from SPI), which contain a polymer thin film with 2 μm periodic holes. The WS2 islands were released from the original Si/SiO2 wafer by two methods, both of which involved etching in 15 M KOH. The first approach34 spin-coats the wafer with a PMMA solution (495k) at 3000 RPM for 30 seconds. The polymer was then allowed to cure overnight at room temperature. The edge of the wafer was marked with a sharp blade to expose the Si/SiO2 surface and the wafer was subsequently immersed in 15 M KOH. The PMMA/WS2 film was released by the effect of the caustic solution and could be fished out with the TEM grid. The TEM grid was then placed on absorbent paper and thoroughly washed with deionized water. Finally, the PMMA was dissolved with acetone droplets. In an alternative PMMA-free approach35, the TEM grid was placed on the Si/SiO2 wafer containing the WS2 islands. One drop of IPA was allowed to dry on the TEM grid and after 10 minutes the wafer was immersed in 15 M KOH. The grid was released and placed on absorbent paper and washed thoroughly with deionized water.
Characterization
WS2 films were characterized by Raman and PL spectroscopies performed in a Renishaw inVia confocal microscope-based Raman spectrometer with a spectral resolution better than 1 cm−1. We used 488, 514.5 and 647 nm laser excitations, keeping the laser power under 0.2 mW at all times. The 520 cm−1 phonon mode from the silicon substrate was used for calibration. The Raman spectra for the bulk were collected from WS2 powder, 99% (Sigma-Aldrich). High-resolution transmission electron microscopy was carried out in a JEOL 2010F equipped with an energy dispersive X-ray (EDX) spectrometer, with an accelerating voltage of 200 kV, field-emission source, ultra-high resolution pole piece (Cs = 0.5 mm) and a 1.9 Å Scherzer limit. SEM observations were performed in a FEI XL30 SEM at 6 kV and an LEO 1530 FESEM operated at 1 kV. Non-contact atomic force microscopy was performed in a MFP-3D-SA from Asylum Research.
Theoretical modeling
Electronic structure calculations are carried out using density functional theory in the local density approximation, with the Ceperley and Adler exchange correlation functional parametrized by Perdew and Zunger, as implemented in the plane-wave code CASTEP36 within Materials Studio 5.5 (software by Accelrys at accelrys.com). The structures are geometrically optimized until the energy difference reached 5 × 10−6 eV/atom with a maximum force of 0.01 eV/Å. The plane wave cutoff energy was 720 eV with a norm-conserving pseudopotential on a grid of 9 × 9 × 2 k-points and a FFT grid of 30 × 30 × 108 for the WS2 crystal and 30 × 30 × 180 for the WS2 isolated layer; (the WS2 layer has a larger cell in the c direction). The phonon density of states and dispersion curves were calculated with the above parameters using density functional perturbation theory as implemented in CASTEP, using a linear response methodology that works well for insulators37.
The optimized unit cell lattice parameters for the WS2 crystal are a = b = 3.147Å and c = 12.167 Å, while the experimental values reported are: a = b = 3.153 Å and c = 12.323 Å.38 For the WS2 monolayer, the calculated a and b parameters (a = b = 3.146 Å) are almost the same as those for the bulk crystal. The distance between the layers is set to 20 Å to eliminate interlayer interaction.
The double resonant Raman reduced intensities of the 2LA mode were modeled using the Fermi golden rule generalized to fourth order27. Electron-two-phonon-electron, electron-two-phonon-hole and hole-two-phonon-hole processes were considered. The scattering matrix elements were held constant, so that, one summand of  of the electron-electron two-phonon process is expressed as:
of the electron-electron two-phonon process is expressed as:

The sum is over k-points k, q-points q, valence bands v, conduction bands c and phonon branches a and β. For the bulk WS2 structure, 234 k-points were used to sample the Brillouin zone, the three highest valence bands, the three lowest conduction bands and two phonon branches over 24 q-points. For monolayer WS2, 234 k-points were also used to sample the Brillouin zone, the two highest valence bands, the two lowest conduction bands and one phonon branch over 12 q-points. The reduced intensity is computed as the sum over all possible processes using the density functional theory band structure after a small rigid shift was applied to the conduction bands to account for the well-known underestimation of the calculated band gap within DFT. Only the electron-two-phonon-electron processes are found to contribute significantly to the difference in intensity between the monolayer and the bulk.
References
Geim, A. K. & Novoselov, K. S. The rise of graphene. Nature Materials 6, 183–191 (2007).
Novoselov, K. S. Graphene: Materials in the Flatland (Nobel Lecture). Angewandte Chemie-International Edition 50, 6986–7002 (2011).
Ci, L. et al. Atomic layers of hybridized boron nitride and graphene domains. Nature Materials 9, 430–435 (2010).
Jin, C. H., Lin, F., Suenaga, K. & Iijima, S. Fabrication of a Freestanding Boron Nitride Single Layer and Its Defect Assignments. Physical Review Letters 102 (2009).
Albe, K. & Klein, A. Density-functional-theory calculations of electronic band structure of single-crystal and single-layer WS2. Physical Review B 66 (2002).
Ding, Y. et al. First principles study of structural, vibrational and electronic properties of graphene-like MX(2) (M = Mo, Nb, W, Ta; X = S, Se, Te) monolayers. Physica B-Condensed Matter 406, 2254–2260 (2011).
Ma, Y. D. et al. Electronic and magnetic properties of perfect, vacancy-doped and nonmetal adsorbed MoSe(2), MoTe(2) and WS(2) monolayers. Physical Chemistry Chemical Physics 13, 15546–15553 (2011).
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically Thin MoS(2): A New Direct-Gap Semiconductor. Physical Review Letters 105 (2010).
Splendiani, A. et al. Emerging Photoluminescence in Monolayer MoS(2). Nano Letters 10, 1271–1275 (2010).
Xiao, D., Liu, G. B., Feng, W. X., Xu, X. D. & Yao, W. Coupled Spin and Valley Physics in Monolayers of MoS2 and Other Group-VI Dichalcogenides. Physical Review Letters 108, 196802 (2012).
Cao, T. et al. Valley-selective circular dichroism of monolayer molybdenum disulphide. Nature Communications 3, 10.1038/ncomms1882 (2012).
Eda, G. et al. Photoluminescence from Chemically Exfoliated MoS(2). Nano Letters 11, 5111–5116 (2011).
Lee, C. et al. Anomalous Lattice Vibrations of Single- and Few-Layer MoS(2). Acs Nano 4, 2695–2700 (2010).
Matte, H. S. S. R. et al. MoS(2) and WS(2) Analogues of Graphene. Angewandte Chemie-International Edition 49, 4059–4062 (2010).
Radisavljevic, B., Radenovic, A., Brivio, J., Giacometti, V. & Kis, A. Single-layer MoS(2) transistors. Nature Nanotechnology 6, 147–150 (2011).
Yin, Z. Y. et al. Single-Layer MoS2 Phototransistors. ACS Nano 6, 74-80 (2012).
Zhan, Y., Liu, Z., Najmaei, S., Ajayan, P. M. & J, L. Large-Area Vapor-Phase Growth and Characterization of MoS2 Atomic Layers on a SiO2 Substrate. Small 8, 966–971 (2012).
Li, H. et al. From Bulk to Monolayer MoS2: Evolution of Raman Scattering. Advanced Functional Materials 22, 1385–1390 (2012).
Lee, Y. H. et al. Synthesis of Large-Area MoS2 Atomic Layers with Chemical Vapor Deposition. Advanced Materials 24, 2320–2325 (2012).
Gutiérrez, H. R. et al. Extraordinary room-temperature photoluminescence in WS2 monolayers. Nano Letters nl3026357 (2012).
Ferrari, A. C. et al. Raman spectrum of graphene and graphene layers. Physical Review Letters 97 (2006).
Gupta, A., Chen, G., Joshi, P., Tadigadapa, S. & Eklund, P. C. Raman scattering from high-frequency phonons in supported n-graphene layer films. Nano Letters 6, 2667–2673 (2006).
Yoon, D. et al. Variations in the Raman Spectrum as a Function of the Number of Graphene Layers. Journal of the Korean Physical Society 55, 1299–1303 (2009).
Najmaei, S., Liu, Z., Ajayan, P. M. & Lou, J. Thermal effects on the characteristic Raman spectrum of molybdenum disulfide (MoS(2)) of varying thicknesses. Applied Physics Letters 100, 013106 (2012).
Molina-Sanchez, A. & Wirtz, L. Phonons in single-layer and few-layer MoS2 and WS2. Physical Review B 84, 155413 (2011).
Gorbachev, R. V. et al. Hunting for Monolayer Boron Nitride: Optical and Raman Signatures. Small 7, 465–468 (2011).
Venezuela, P., Lazzeri, M. & Mauri, F. Theory of double-resonant Raman spectra in graphene: Intensity and line shape of defect-induced and two-phonon bands. Physical Review B 84, 035433 (2011).
Frey, G. L., Tenne, R., Matthews, M. J., Dresselhaus, M. S. & Dresselhaus, G. Optical properties of MS2 (M = Mo, W) inorganic fullerene-like and nanotube material optical absorption and resonance Raman measurements. Journal of Materials Research 13, 2412–2417 (1998).
Sourisseau, C., Cruege, F., Fouassier, M. & Alba, M. 2Nd-Order Raman Effects, Inelastic Neutron-Scattering and Lattice-Dynamics in 2H-Ws2. Chemical Physics 150, 281–293 (1991).
Stacy, A. M. & Hodul, D. T. Raman-Spectra of Ivb and Vib Transition-Metal Disulfides Using Laser Energies near the Absorption Edges. Journal of Physics and Chemistry of Solids 46, 405–409 (1985).
Wang, Y. Y., Ni, Z. H., Shen, Z. X., Wang, H. M. & Wu, Y. H. Interference enhancement of Raman signal of graphene. Applied Physics Letters 92, 043121 (2008).
Beal, A. R. & Liang, W. Y. Excitons in 2H-Wse2 and 3R-Ws2. Journal of Physics C-Solid State Physics 9, 2459–2466 (1976).
Jiang, H. Electronic Band Structures of Molybdenum and Tungsten Dichalcogenides by the GW Approach. Journal of Physical Chemistry C 116, 7664–7671 (2012).
Reina, A. et al. Large Area, Few-Layer Graphene Films on Arbitrary Substrates by Chemical Vapor Deposition. Nano Letters 9, 30–35 (2009).
Regan, W. et al. A direct transfer of layer-area graphene. Applied Physics Letters 96, 113102 (2010).
Clark, S. J. et al. First principles methods using CASTEP. Zeitschrift Fur Kristallographie 220, 567–570 (2005).
Refson, K., Tulip, P. R. & Clark, S. J. Variational density-functional perturbation theory for dielectrics and lattice dynamics. Physical Review B 73, 155114 (2006).
Schutte, W. J., Deboer, J. L. & Jellinek, F. Crystal-Structures of Tungsten Disulfide and Diselenide. Journal of Solid State Chemistry 70, 207–209 (1987).
Acknowledgements
M.T., H.R.G., A.L.E. and V.H.C. acknowledge funding from the U. S. Army Research Office MURI grant W911NF-11-1-0362. This research was partially supported by the Materials Simulation Center of the Materials Research Institute, the Research Computing and Cyberinfrastructure unit of Information Technology Services. MT acknowledges JST-Japan for funding the Research Center for Exotic NanoCarbons, under the Japanese regional Innovation Strategy Program by the Excellence. M.T. and V.H.C. also acknowledge support from a Penn State Center for Nanoscale Science Seed grant on 2-D Layered Materials (DMR-0820404). This publication was also supported by the Pennsylvania State University Materials Research Institute Nanofabrication Lab and the National Science Foundation Cooperative Agreement No. ECS-0335765. Electron microscopy characterization facilities within the Materials Research Institute at the Pennsylvania State University were also used for this research. A.R.B.M. and J.-C.C. acknowledge financial support from the F.R.S.-FNRS of Belgium. This research is directly connected to the ARC on « Graphene StressTronics » sponsored by the Communauté Française de Belgique.
Author information
Authors and Affiliations
Contributions
M.T., H.T. and H.R.G. designed the experiments. The synthesis of the samples was carried out by N.P.L., H.R.G. and A.L.E. The Raman spectra were acquired by A.B. and H.R.G. Theoretical calculations were performed by H.T., F.L.U., A.R.B.M., J.-C.C., V.C. and C.-I.C. AFM characterization was performed by B.W. and H.R.G. TEM sample preparation was carried out by A.L.E. and H.R.G. TEM observations were carried out by H.R.G. SEM characterization was carried out by A.L.E. and N.P.L. All the authors contributed to the manuscript preparation and discussion of results.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Berkdemir, A., Gutiérrez, H., Botello-Méndez, A. et al. Identification of individual and few layers of WS2 using Raman Spectroscopy. Sci Rep 3, 1755 (2013). https://doi.org/10.1038/srep01755
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01755
This article is cited by
-
Observation of single-molecule Raman spectroscopy enabled by synergic electromagnetic and chemical enhancement
PhotoniX (2024)
-
Strain tuning MoO3 vibrational and electronic properties
npj 2D Materials and Applications (2024)
-
Vertical two-dimensional WS2 flakes grown on flexible CNT film for excellent electrochemical performance
Rare Metals (2024)
-
WS2(RE)/Si2(X)H co-doped heterojunctions for wide-spectrum and high-performance photodetections
Journal of Optics (2024)
-
Tungsten disulfide and reduced graphene oxide composite as efficient catalyst for the reduction of picric acid in aqueous media
Journal of Materials Science (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.