Introduction

Acentral issue arising in the context of networked systems is the ability to efficiently control, track, or detect the behavior of the constituent nodes of a network. In static networks or slowly evolving networks, a solution to this problem often involves computing a dominating set of the network. A dominating set of a network (graph) with node set V is a subset of nodes S ⊆ V such that every node not in S is adjacent to at least one node in S. Example problems in whose solution the dominating set (or some variant of it) has been shown to play a part include optimal sensor placement for disease outbreak detection1, controllability of networks2 and social influence propagation3,4. The smallest dominating set of constitutes its minimum dominating set (MDS). Thus, the MDS of a network is the smallest subset of nodes such that every node of the network either belongs to this subset or is adjacent to at least one node in this set. The MDS is an important construct if the inclusion of members into the dominating set comes at a certain non-zero cost. For example, in the case of network sensor placement, if placing a sensor has a non-zero cost and if each sensor can eavesdrop on all its neighbors, then the MDS nodes define the lowest cost placement that allows all nodes to be monitored. Continued interest in network control, detection and efficient spreading or curbing of network flows motivates our interest in understanding the scaling behavior of the MDS on stylized network models of real networks.

In particular, we focus on the properties of the MDS in scale-free networks that are characterized by a power law degree distribution (P(k) ~ k−γ). These networks constitute a class of stylized networks which bear strong resemblance to several real-world networks including social, infrastructural and biological networks. Typically, values of the power law exponent γ lie in the range 2 < γ < 35,6, although there are few examples of networks with γ < 2 value; for example the co-authorship network in high-energy physics7 and some email networks8. Several algorithms have been developed and used in previous works to generate scale-free networks. Most of these methods are more general solutions to the problem of constructing a network from any prescribed degree distribution9,10, applied to a power-law degree distribution.

The mathematical literature focusing on bounds on dominating sets is vast11. In most prior works (with the exception of12 to be discussed below), the MDS has not been studied systematically for scale-free networks over a significantly varying range of γ. For example, Cooper et al.13 studied the behavior of MDS size on the special class of scale-free networks generated by preferential attachment14 (corresponding to γ = 3) and found that minimum dominating sets as well as minimum h-dominating sets (where every node needs to be dominated at least h times) have sizes that are bounded above and below by functions linear in N, where N is the number of nodes in the network. Other studies have focussed on MDS sizes for random regular graphs and Erdős-Rényi (ER)15 graphs. Zito16 studied the size of the minimum independent dominating set on r-regular random graphs (with 3 ≤ r ≤ 7) and showed that the size of this set (and therefore the MDS) is upper bounded by a linear function of N. Recently, Bíró et al.17 improved the pre-factor of the O(N) bound of the size of the MDS in r-regular graphs based on a greedy algorithm18,19,20,21. Wieland et al.22 derived general bounds for dense ER graphs (with fixed edge probability), showing that the MDS size scales as log N (with no direct applicability to sparse graphs with fixed average degree).

A recent study12 has focused on the behavior of the MDS size on model scale-free networks with varying degree exponent, as well as empirical networks. The authors employed the Havel-Hakimi algorithm23,24 with random (Monte-Carlo) edge swaps25 (HHMC) for constructing synthetic networks and they used a binary integer programming method to obtain the MDS. They reported that the MDS size decreases as γ is lowered, making heterogeneous networks very easy to control. However, our study of a variety of scale-free network families suggests a more complicated picture. In particular, we find that details of the network generation process and the choice of the maximum degree cutoff, bear an enormous influence on the dependence of MDS size on γ, even when the average degree 〈k〉 is kept fixed. The latter constraint is motivated by the need of comparing networks (from the MDS perspective) with the same amount of “resources”, i.e., fixed average edge-cost per node, or equivalently, fixed average degree in unweighted networks. Naturally, for γ < 2 and fixed average degree, there is only a finite (but large) parameter range in terms of γ and N with realizable networks. Nevertheless, motivated by the existence of several such real-world sparse networks26,27, we also investigate networks from various ensembles in this regime and, in particular, how easy or hard it is to dominate them. On the other hand, when keeping the minimum degree fixed in this regime, the number of edges increase faster than the number of nodes and those networks are becoming inherently easy to dominate. For γ > 2 keeping the average or the minimum degree fixed are equivalent constraints in the large network-size limit.

Finding the exact MDS is one of the well-known NP-hard problems of graph theory. While it has been proven that finding a sublogarithmic approximation to the MDS is also NP-hard, a logarithmic approximation of the MDS28 can be found by a simple greedy algorithm18,19,20. The greedy algorithm is ideal for practical applications as it provides a logarithmic approximation for the MDS and runs in time linear in the number of edges. This is certainly superior in comparison to binary integer programming-based methods (used in Ref. 12) that have unknown (network structure dependent) polynomial run time, exponential run time in the worst case and yield no significantly better approximation to the MDS size in finite waiting time than the greedy algorithm, according to our experiments.

In practice, one could imagine a scenario where rather than dominating all nodes of the network, it is sufficient to dominate some (large) fraction of nodes. This reduces to the problem of finding a partial minimum dominating set (pMDS)29 which is the smallest subset of nodes (and possibly a subset of the full MDS) such that at least some given fraction of the nodes are either in the set or adjacent to a node in this set. We investigate the scaling of both the MDS as well as the pMDS with respect to the network size N.

Results

We start with a short description of the three network construction methods that we utilize to generate three classes of networks with the same power-law degree distribution and a predefined average degree. Each method is a general degree sequence sampling method applied to degree sequences drawn from discrete power-law distributions with predefined parameters. The degree sequence is treated as a list of stubs (half-edges) for each node; pairs of stubs are connected to form edges. The methods are identified by four-letter abbreviations and are as follows:

  • Configuration model10,9 (CONF networks), where we randomly pick any two edge stubs and connect them, until there are no more stubs to connect. This results in a multigraph; we reduce multiple links to single links and remove self loops, to get a simple graph.

  • a Markov chain Monte Carlo method25 (HHMC networks), where we first build a simple graph deterministically by the Havel-Hakimi algorithm and then we randomize the links by swapping pairs of edges. The number of the attempted edge swaps is four times the number of edges in the network (see Supplementary Information Sections S.1 and S.4).

  • a sequential algorithm that generates samples from all possible realizations of a given degree sequence30 (DKTB networks, named after the authors). The DKTB graph-construction algorithm is based on the underlying theorems proven in Ref. 31.

We use two possible subclasses of each network class, according to the maximum degree cutoff kmax. Either there is no explicit cutoff, having kmax = N − 1 (where N is the network size), or we use a structural cutoff , resulting in uncorrelated scale-free networks32,33. When we have the cutoff, we indicate it in the name of network type as cCONF, cDKTB, or cHHMC, where c stands for cutoff.

As indicated in the results and in our figures, the average degree of each individual network is kept fixed at a predetermined value throughout all samples of each dataset. Details on controlling the average degree are included in the Methods section, technical data is provided in the Supplementary Information, Section S.3.

Results shown in the next subsections are generated by running a sweep of network size N and power-law exponent γ values, generating hundreds of network realizations and averaging MDS size among them for each parameter combination. The MDS of each individual network is found by a greedy algorithm.

MDS scaling with network size

Figures 1(a)–(c) show the MDS size for networks without any explicit upper cutoff on degree (kmax = N − 1). For CONF networks, the MDS size scales linearly with N for all γ values. In striking contrast, DKTB networks and HHMC networks show a marked transition in the scaling behavior at γc ≈ 1.9. For γ > γc, MDS size scales linearly with N, whereas for γ < γc, the MDS size appears to lose its dependence on N in the asymptotic limit. Figures 1(a)–(c) focus on a subset of all considered γ values, which range from γ = 1.6 to 3.00, to clearly show the scaling transition for DKTB and HHMC networks.

Figure 1
figure 1

The size of MDS scaling with N, 〈k〉 = 14, for all network types, averaged over 400 network realizations with 5 greedy searches for each at every data point.

The figure insets show the same data on log-log scales. Error bars are shown for all data points (however, they may be very small and hidden by the larger symbols).

Full size image

Figures 1(d)–(f) show in contrast that with the structural degree cutoff, , for all network classes the MDS size scales linearly with N irrespective of the γ value.

To better understand this scaling, we can derive a lower bound for the MDS size by considering a “best case scenario” for dominating the network. We use the continuous probability density function fK(k) equivalent to the discrete degree distribution and we define l(k′) as the expected number of nodes above a certain degree threshold k′:

In the “best case”, the neighborhoods of these nodes are disjoint sets (not overlapping) and therefore each node with degree k dominates k + 1 nodes (itself and its neighbors). Then we can find the appropriate degree threshold to ensure the domination of all nodes by the following:

Therefore, l(k*) sets a lower bound for the size of MDS. Note, that these formulae can be used with any degree distribution and k* can always be found numerically. Figure 2 shows the l(k*) bounds for power-law distributions as a function of N with 〈k〉 = 10.

Figure 2
figure 2

The scaling of the calculated lower bound of MDS size in power-law distributions, for various power-law exponents, 〈k〉 = 10.

(a) kmax = N − 1, (b) . Figure insets show l(k*) bounds on log-log scales. See Supplementary Information (S.7) for details.

Full size image

There are multiple consequences of the lower bound's scaling. For kmax = N − 1 networks, the possibility of an O(N)-to-O(1) transition of MDS size is supported by l(k*) (Fig. 2): it exhibits an O(1) behavior for γ < 2, while it progresses to a linear scaling with N for γ > 2 [Fig. 2(a)], similar to the results of DKTB and HHMC networks. For networks with , when γ < 2 and l(k*) ~ N when γ > 2. Note, however, that the convergence to the asymptotic behavior is extremely slow for 2 < γ < 3 [see insets of Figs. 2(a) and (b)]. Thus, for the case of structural cutoff, the lower bound indicates that the MDS size can never become O(1) and we cannot expect a sharp scaling transition. Derivation of the asymptotic behavior of l(k*) is included in the Supplementary Information (Section S.7).

Scaling of partial dominating sets

Next, we study the scaling behavior of the partial MDS size with N as we vary the value of the required dominated fraction z. In Figure 3, we present results for the DKTB class of networks; our findings are qualitatively similar for CONF and HHMC network classes and networks with . Results for these networks are shown in Supplementary Information (Figs. S7 and S8).

Figure 3
figure 3

The size of partial MDS scaling with N, 〈k〉 = 14, averaged over 400 network realizations and 5 greedy searches for each, (a) DKTB, γ = 1.7, (b) DKTB, γ = 2.5, (c) cDKTB, γ = 1.7, (d) cDKTB, γ = 2.5.

The dominated fraction of nodes is expressed as percentage of the network size. Error bars are shown for all data points (however, they may be very small and hidden by the larger symbols).

Full size image

Below a certain value of , where is the highest realized degree in the network, the pMDS trivially contains only the node with highest degree. Apart from this trivial case, for , the size of the pMDS exhibits the same scaling as the full MDS in the different γ regimes (Fig. 3). In other words, DKTB and HHMC networks display a transition in the scaling behavior of pMDS size from linear dependence on N to virtually no dependence on N at γ ≈ 1.9, while CONF networks always show a linear scaling of pMDS size with N.

For a baseline-comparison to the partial MDS size obtained by greedy algorithm, we also study the expected number of nodes needed to dominate a given fraction of the network using random node selection, giving a partial random dominating set (pRDS). We run the random search five times on each realization to obtain an expected RDS size. Figure 4 compares pRDS with pMDS, showing that a simple random node selection gives approximately an order of magnitude larger dominating set than the greedy method. Note also, that in order to reach full domination using random node selection, we would need to include almost all nodes of the network in the dominating set. Further, for reference, in Fig. 4 we also show the known upper bound, obtained for optimized random selection of the dominating set (oRDS)18 but also applicable to the greedy algorithm11,18,19, for a graph with minimum degree kmin: . Note, that in our network construction schemes with fixed average degree, kmin = kmin(N, γ, 〈k〉), hence the small jumps in the above bound when plotted as a function of N for fixed γ and 〈k〉.

Figure 4
figure 4

Comparison of partial MDS and partial RDS scaling with N for DKTB (a, b) and cDKTB (c, d) networks (without and with structural cutoff, respectively); 〈k〉 = 14, averaged over 400 network realizations and 5 greedy searches for each.

The dominated fraction of nodes is expressed as a percentage of the network size. For reference, we also show the upper bound (dashed lines) for an optimized random dominating set (oRDS)11,18 (see text).

Full size image

MDS scaling with power-law exponent

To measure the dependence of MDS size on γ, we find the MDS for a fixed network size of N = 5000 nodes. Results for various 〈k〉 values are presented in Figure 5(a) for networks with no structural cutoff and in Figure 5(b) for networks with a structural cutoff.

Figure 5
figure 5

The size of MDS as a function of γ for various network types and average degrees, N = 5000, averaged over 200 network realizations with 5 greedy searches for each at every data point.

(a) for networks with no degree cutoff; (b) for networks with the structural cutoff. (c) shows the scaled MDS size vs. γ for HHMC networks with 〈k〉 = 14 for various system sizes. (d) Scaled MDS size for the largest network and the best-fit power-law (solid red curve) in the vicinity of (and above) the transition point, |MDS|/N ∝ (γ − γc)β with β ≈ 0.37. Inset: same data as in (d) after shifting the horizontal axis and on log-log scales.

Full size image

We find a surprising trend in several cases. Perhaps, most intriguing is the trend seen in the case of CONF networks where the MDS size appears to have a non-monotonic dependence on γ. Traversing increasing γ values on a coarse scale, the MDS size starts out large at low γ, reaches a global minimum in the range 1.9 < γ < 2.3 and then grows again as γ increases. However, generating network samples with a finer resolution of γ values (Δγ = 0.01, reaching the resolution of error between desired and achieved γ values), we also notice the existence of kinks in addition to the large scale non-monotonicity.

By probing the dependence of MDS size on γ for DKTB and HHMC networks at fine resolution similar to one used for CONF, we find only minor traces of kinks, but they are within the error margin of MDS size. On a coarse scale, we find quantitatively similar results for both network classes. The MDS size curve is flat at very low values of γ and then increases steadily beyond γ ≈ 1.9. When γ > 3, the MDS size of all three network types converge to the same value, indicating that beyond this point the structure of these networks are very similar [Fig. 5(a)].

The dependence of MDS size on γ is strikingly different for networks with a structural cutoff [Fig. 5(b)]. In this case, all three network classes show identical results for given network parameters. For increasing γ values the size of MDS first decreases, then reaches its minimum at approximately 2.5 < γ < 3.0 and increases again when γ > 3. Since all three classes display almost indistinguishable results, we can infer that these networks are structurally very similar. Kinks like those seen in CONF networks are also observed here, but with a much smaller amplitude.

In the vicinity of (and above) the transition point, we also found that for sufficiently large DKTB (not shown) and HHMC [Fig. 5(c)] networks, the scaled MDS size can be reasonably well approximated with a power-law,

with β ≈ 0.37 [Fig. 5(d)] (see Discussion and Supplementary Information S.10 for further details).

Discussion

As demonstrated clearly by the results, the specific method used for generating a network ensemble has a profound influence on the MDS size. This suggests that there are distinctive features in the structures of networks generated by the different classes. From the details of the generation methods, it might appear that DKTB and HHMC classes produce networks that are similar in structure and this is certainly corroborated by our results. However, their distinction from networks in the CONF class seems to disappear when a structural cutoff is introduced in the degree distribution. Although we cannot rigorously demonstrate that particular structural features are responsible for the observed scaling behavior, we conjecture on the origin of the distinct behaviors shown in the Results.

It should be noted that Del Genio et al.34 have shown the non-existence of realizable graphs with a power-law degree sequence with 0 ≤ γ ≤ 2. However, as they point out, their arguments refer to the situation where the prescribed degree sequence has to be perfectly satisfied. In our methods, networks with 1 ≤ γ ≤ 2 are realized by removing some edge stubs from the degree sequence that cause nongraphicality. For CONF networks, pruning of multiple links and self loops perform this task, while for DKTB and HHMC networks, a Havel-Hakimi-based graphicality correction algorithm is applied (see Methods and Supplementary Information Section S.1 for details). It is notable, that we can choose appropriate parameters such that even after pruning, or graphicality-preserving stub removal, we have a network whose degree distribution (in particular, its tail) approximates the desired power-law. (For the degree distribution of the networks obtained this way, see Supplementary Information S.9.) As a result of these procedures, our networks in this range of γ are not exact realizations of perfect power-law degree sequences and therefore do not contradict the fundamental results of Ref. 34.

When the structural cutoff is not imposed on the degree sequence, the non-graphicality below γ = 2 plays an important role in the scaling transition of the MDS size with N. When γ < 2, there are too many edge stubs in the prescribed degree sequence and some of them have to be removed to resolve nongraphicality. Different network construction methods solve this problem differently. With respect to MDS scaling behavior, the key difference is in the treatment of the highest degrees. In case of CONF, the formation of multiple links is allowed during the stub connection process and the duplicate links are pruned later. Since the realized multiple links predominantly connect stubs belonging to high-degree nodes with each other33,35, the large degrees of the hubs are effectively wasted in connections that do not improve their potential to dominate. Furthermore, as a consequence, the interconnections of low degree nodes become more dominant, forming a relatively sparse web, which necessitates the inclusion of many nodes in the dominating set, preventing it to become O(1). However, in case of the Havel-Hakimi-based graphicality correction (used in HHMC and DKTB methods) the stubs of the highest degree nodes are connected first, ensuring that these nodes are present in the network as hubs. The MDS scaling transition can therefore be explained by the scaling of the largest realized degree (also known as the natural cutoff of the degree sequence), 33,36. When γ < 2, the MDS size becomes O(1) because the largest degree and potentially the second and third largest degrees become O(N) and the network is dominated by these nodes. In essence, we find that the domination transition is directly related to the underlying graphicality transition34: the same underlying structural properties which are responsible for the graphicality transition34 in the infinite network-size limit allow for the O(N)-to-O(1) domination transition for large but finite DKTB and HHMC networks. In other words, those finite DKTB and HHMC network realizations which happen to exist for γ < 2 can be dominated by an O(1) MDS. The sharp emergence of the O(N) minimum dominating set (and the existence of the domination transition) is also supported by the power-law behavior of the scaled MDS size just above the transition point [Fig. 5(d)].

The small difference between our numerically observed value of the domination transition at around γ ≈ 1.9 and the γ = 2 value of the graphicality transition34 might lie in finite-size effects and in the log(N) accuracy of the greedy algorithm with respect to the size of the true MDS [Figs. 5(c) and (d)].

The different treatment of largest degrees in different network classes can be illustrated by plotting against γ, see Figure 8. Note, that for the theoretical value we need to derive and evaluate the exact formula from the degree distribution, see Supplementary Information Section S.6. Further, the markedly different structure of CONF networks compared to HHMC and DKTB networks in the absence of a structural cutoff also shows up in the network visualizations in Fig. 6.

Figure 6
figure 6

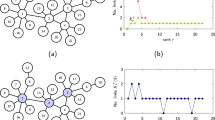
Visualization of typical scale-free networks of each type with kmax = N − 1 at three different power-law exponent values, embedded by the SFDP layout engine of Graphviz visualization software37.

In all networks, N = 1000 and 〈k〉 = 14; the colored nodes belong to the MDS.

Full size image
Figure 7
figure 7

Visualization of typical scale-free networks of each type with at three different power-law exponent values, embedded by the SFDP layout engine of Graphviz visualization software37.

In all networks, N = 1000 and 〈k〉 = 14; the colored nodes belong to the MDS.

Full size image
Figure 8
figure 8

Scaling of maximum realized degree with power-law exponent γ, for various network sizes.

(a) theoretical expected value from power-law distribution, (b) degree sequence with graphicality correction (HHMC and DKTB networks), (c) degree sequence after pruning multiple links (CONF networks).

Full size image

In contrast, with the structural cutoff, networks generated using the three different methods appear to share similar structure as can be seen in Fig. 7, from the similar scaling of MDS size with N and the dependence of MDS size on γ. The restrictive cutoff precludes the scaling of MDS size from becoming O(1), as shown by the l(k*) lower bound in Fig. 2(b).

The non-monotonic behavior of the size of the MDS with γ (with the exception of the DKTB and HHMC constructions with no maximum degree cutoff) are in part the consequence of the stringent constraint of resources for domination (fixed average degree, i.e., fixed number of edges for fixed N): for small and decreasing values of γ, while maintaining a fixed average degree for a given network size N, the minimum degree decreases and there are O(N) number of such nodes. However, in the DKTB and HHMC networks the largest hub can have O(N) links and it has the potential alone to connect to (and dominate) the nodes with the lowest degree, hence the monotonic behavior with γ (and the transition to O(1) domination) for these networks [Fig. 5(a)].

Kinks seen in the curves of MDS size when plotted against γ are the result of controlling the average degree with very high precision. Smooth change of the control parameters introduces gradual changes in the network structure, however, the average degree does not change smoothly (although it is monotonic; see Supplementary Information Section S.3). Conversely, when we probe a range of γ values, we need a smooth control over the average degree, requiring non-smooth changes in control parameters and hence in the network structure. Therefore, we can expect that any structure-dependent quantity, like the MDS size, will show kinks with respect to γ.

The results reported by Nacher et al.12 suggest that for a given 〈k〉, decreasing γ results in a monotonic lowering of the MDS size. However, they only studied the HHMC method of network generation with a variable cutoff. By introducing a well-defined structural cutoff and in addition studying two other classes of networks, we show that precise details of the network construction have a strong impact on the trend in MDS size as γ is varied.

In summary, we have shown through extensive numerical experiments, that the size of the minimum dominating set approximated by a greedy algorithm undergoes a transition in its scaling with respect to N only for particular methods of network construction in the absence of a structural cutoff. For the configuration model construction, or the other construction methods with a structural cutoff, no such transition is observed. However, intriguingly, in the presence of a structural cutoff, the MDS size increases as γ is lowered below 2. Thus our results demonstrate that it is not sufficient to have a scale-free network with γ < 2 to have an easily dominated (easily controllable) network; intricate details in the wiring of the network must also be taken into consideration.

Methods

As the first step of network construction, we generate a discrete power-law degree distribution and we also calculate the cumulative distribution function (CDF) associated with the desired discrete power-law degree distribution. Then, using inverse sampling of the CDF, we generate the degree sequence of the network. We find that using a discrete distribution results in much better accuracy of the desired power-law exponent than sampling degrees from a continuous distribution with rounding.

Once the degree sequence is generated, each node is assumed to have as many edge stubs as its degree. The process of network generation connects pairs of edge stubs to form edges, the three network construction methods (CONF, DKTB, HHMC) carry out this task differently, according to their specific algorithms. In CONF and DKTB, the random selection of edge stubs gives a random realization of the degree sequence. In contrast, the HHMC method connects edge stubs deterministically (using the Havel-Hakimi algorithm) and a random realization is obtained by a Markov chain of swapping edge pairs. The mixing time of this Markov chain is determined empirically, see Supplementary Information (Section S.4).

HHMC and DKTB methods are “exact methods” since they do not alter the given degree sequence while constructing the network. Therefore, we must supply them with graphical degree sequences, i.e. sequences for which it is assured that a simple graph realizing that sequence exists. To ensure graphicality, we devised a graphicality correction method (See Supplementary Information, Alg. 1 in S.1), based on the Havel-Hakimi algorithm. The goal of the original algorithm is to test the graphicality of a degree sequence. It reports failure when some stubs of a node cannot be connected to other nodes. Instead of reporting failure, we simply remove these stubs from the degree sequence, making the remaining sequence graphical. This correction precedes the network construction step for HHMC and DKTB networks, but it is not needed for CONF networks, because every degree sequence is graphical for a multigraph. We effectively remove any non-graphicality of the degree sequences when we remove multiple links and self loops to create a simple graph.

The final step of network generation is to ensure that we have a single connected component. Further details are provided in Supplementary Information Section S.1, including a flow diagram that illustrates all steps of the network generation procedure.

We control the average degree of the networks by setting an appropriate lower degree cutoff kmin. In order to have a very fine control over the average degree, we also remove a given fraction f of the lowest degrees from the degree distribution, . To calibrate which kmin and f values result in which average degrees, we constructed a high-accuracy lookup table by generating network samples for all possible parameter combinations of kmin, f, N and γ, for all network classes. By numerically inverting this table, we can find the needed parameters to achieve any desired average degree for any given network class. Details on this construction, the corresponding lookup table and achieved accuracy are included in the Supplementary Information (Section S.3).

Note, that the smallest reachable γ is defined by 〈k〉. The average degree of a network increases rapidly as γ decreases for given kmin (see Figure S2 in the Supplementary Information) and for a given γ the lowest 〈k〉 is obtained when kmin = 1. Consequently, for a fixed 〈k〉, the lowest possible γ is the value at which the 〈k〉 vs. γ curve for kmin = 1 attains the desired 〈k〉. This lower limit on γ for each 〈k〉 can be determined from the lookup tables. We study the MDS scaling behavior in 8 ≤ 〈k〉 ≤ 16 range, because it allows for a wide range of γ values.

Since finding the MDS is NP-hard, we approximate the exact solution by using a sequential greedy algorithm. Starting with an empty set , at each step the algorithm adds that node to which yields the largest increase in the number of dominated nodes in the network. When there are multiple candidate nodes yielding the maximal increase in domination, the algorithm chooses one randomly (uniformly among candidates). These steps continue until all nodes are dominated and then the algorithm terminates with storing the approximated MDS. The greedy algorithm yields a (1 + log N) approximation28 to the size of MDS and has a time complexity of O(E). See the Supplementary Information for implementation details.

We found that the MDS sizes given by the greedy algorithm for any single network follow approximately a Gaussian distribution, with at least an order of magnitude smaller standard deviation than the standard deviation of average MDS size among multiple network samples. (See distributions and histograms obtained by the greedy search in the Supplementary Information, section S.8.) Therefore, for any given network, we find it sufficient to run the greedy algorithm five times, to obtain a reliable estimate of the average MDS size. Similarly obtained results for all network realizations for a given combination of parameter values and a given network class are averaged to obtain an estimate of the mean greedily approximated MDS size.

In order to find the pMDS for a given dominated fraction z, we use the same greedy approach as for the full MDS, except that we terminate the algorithm when the desired fraction of nodes are dominated.