Abstract
Earth's cusp proton aurora occurs near the prenoon and is primarily produced by the precipitation of solar energetic (2–10 keV) protons. Cusp auroral precipitation provides a direct source of energy for the high-latitude dayside upper atmosphere, contributing to chemical composition change and global climate variability. Previous studies have indicated that magnetic reconnection allows solar energetic protons to cross the magnetopause and enter the cusp region, producing cusp auroral precipitation. However, energetic protons are easily trapped in the cusp region due to a minimum magnetic field existing there. Hence, the mechanism of cusp proton aurora has remained a significant challenge for tens of years. Based on the satellite data and calculations of diffusion equation, we demonstrate that EMIC waves can yield the trapped proton scattering that causes cusp proton aurora. This moves forward a step toward identifying the generation mechanism of cusp proton aurora.
Similar content being viewed by others
Introduction
The magnetospheric cusp plays an essential role by acting a most direct connection between the ionosphere and the interplanetary medium through magnetic reconnection1. Magnetic reconnection tends to occur whenever the directions (or at least one component) of magnetospheric and interplanetary magnetic fields become antiparallel2. During reconnection, magnetic field lines in the subsolar region become open via connecting the solar wind magnetic field. Following the open filed line, solar energetic protons can leak through the magnetopause and enter the Earth's cusp region3,4. However, a minimum magnetic field exists off the equator in the high latitude dayside cusp region5, allowing the protons with higher perpendicular velocities to be trapped there due to the first adiabatic invariant (Fig. 1). A key unanswered question, both theoretically and observationally, is how the protons escape from the cusp region. Proton precipitation into the atmosphere requires a scattering mechanism that violates the first adiabatic invariant. The scattered protons are subsequently removed at low altitude by collisions with the neutral atmosphere, causing the cusp proton aurora. In the basically collisionless magnetosphere, such scattering occurs during interactions with plasma waves. One important plasma wave, electromagnetic ion cyclotron (EMIC) wave is capable of interacting with protons, efficiently scattering protons into the atmosphere6. However, it has not been possible so far to identify whether the EMIC wave is indeed responsible for the cusp proton aurora, because there has been a lack of information on the power and distribution of the EMIC wave in the cusp region. The notable events that occurred on April 21, 2001, perhaps provide an excellent opportunity to identify such mechanism.
Results
On April 21, 2001 an interplanetary coronal mass ejection (CME) started to interact with the magnetosphere when Cluster spacecrafts were traveling around the cusp region. This interaction produced a strong magnetic storm (Dst = −103 nT) in the Earth.
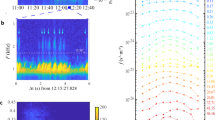
Figure 2a shows proton fluxes at two different indicated energies of 6.5 and 10.53 keV collected by CIS instrument onboard Cluster satellites. When Cluster satellite travels into the cusp region at 21:45 UT, proton fluxes are observed to be greatly enhanced by a factor of ~ 103 higher than those in the adjacent region and remained at a high level until around 22:53:00 UT when Cluster satellite approaches the cusp boundary layer.
Satellite data on 21 April 2001 storm.
(a), Proton fluxes at different indicated energies collected by CIS instrument onboard Cluster satellites. The arrow denotes the time (21:45 UT) when Cluster satellite travels into the cusp region. Proton fluxes are greatly enhanced in the cusp region by a factor of ~ 103 higher than that in the adjacent boundary region. The vertical line indicates the time (22:53 UT) when a steep drop in flux occurs, corresponding to the cusp boundary. The shaded region represents occurrence of the observed enhanced electromagnetic ion cyclotron (EMIC) waves (b) and the cusp proton aurora (c–h). (b), EMIC wave data collected by the Cluster FGM instrument for 10 minutes duration. EMIC waves are left hand polarized electromagnetic waves at frequencies below the proton gyrofrequency. The color bar on the right gives the wave power spectral density for the wave magnetic field. The wave power changes dramatically and maximizes basically at frequencies from 0.1–0.5 Hz. The white line denotes the local proton cyclotron frequency fcp (fcp = qB/(2πmp)), where q is the proton charge, mp is the proton rest mass and B is the ambient magnetic field strength. (c–h), Auroral snapshots as a function of magnetic local time (MLT) and magnetic latitude (MLat) obtained by FUV-SI12 onboard IMAGE spacecraft. The arrow indicates the location of the cusp proton aurora at each time. Cusp proton aurora occurs basically in 11:00 MLT and ~ 70°–80° MLats and are shifted to the noon sector.
Figure 2b shows strong wave (identified as EMIC) activities for 10 minutes duration observed by FMG instrument onboard Cluster satellite. The power spectrum of EMIC wave is obtained by performing a wavelet coherence analysis7. The wave power changes dramatically and maximizes basically at frequencies from 0.1–0.5 Hz, corresponding to the typical EMIC wave frequency range.
Figures 2c–h show the brighten and intensified proton aurora in the dayside cusp region (12 MLT, latitude between 70 and 88) observed by FUV-SI12 instrument onboard IMAGE spacecraft8 when IMAGE spacecraft travels in the region 65~70 MLat. The SI12 instrument detects the Doppler-shifted Lyman-α photons corresponding to precipitating charge-exchanged protons with energies of a few keV. After 22:45 UT, the proton aurora in the dayside cusp region began to brighten and lasted for ten minutes until 22:55 UT. The high latitude proton cusp aurora in this case was shifted to the noon sector (around 12 MLT) and to higher latitude (towards 80), consistent with the previous observations9,10.
An important feature of this event is that the proton fluxes drop dramatically and the cusp proton aurora are intensified during the period from 22:44:18 UT to 22:55:30 UT, corresponding to the occurrence of strong EMIC wave activities. Since the typical energy for the cusp proton aurora lies in the range ~ 5–10 keV, such correlated data above suggests that the dramatic depletion in proton fluxes and the intensified cusp proton aurora should be strongly associated with enhanced EMIC waves.
In the quasi-linear theory, cyclotron wave-particle interactions occur when the wave frequency equals a multiple of the particle gyrofrequency in the particle reference frame. These cyclotron wave-particle interactions yield efficient exchange of energy and momentum between the waves and particles, causing particle scattering. Cyclotron wave-particle interactions can be described via pitch angle and momentum diffusion coefficients. Then, the temporal evolution of the particle distribution function can be obtained by evaluating the diffusion coefficients and solving the Fokker-Planck diffusion equation11. Here, we use this approach to simulate changes in the protons distribution following their injection into the cusp region.
To calculate the diffusion coefficients by EMIC waves, a detailed knowledge of the amplitudes and spectral properties of the waves is required. Here, we assume that the wave spectral density follows a typical Gaussian frequency distribution12, with a center fm, a half width δf, a band between f1 and f2. Considering that EMIC waves vary dramatically in this event (Fig. 1b), we choose two representative times and present a least squares Gaussian fit to the observed spectral intensity, together with the corresponding fitting parameters (Fig. 3).
Gaussian Fitting curves.
Wave power spectral intensity  versus frequency at two representative times 22:48:39 UT (upper) and 22:51:37 UT (lower). Modeled Gaussian fit (solid) to the observed spectra (dot) is shown, together with the fitted wave amplitude Bt, the peak wave frequency fm, the bandwidth δf, the lower and upper bands f1 and f2.
versus frequency at two representative times 22:48:39 UT (upper) and 22:51:37 UT (lower). Modeled Gaussian fit (solid) to the observed spectra (dot) is shown, together with the fitted wave amplitude Bt, the peak wave frequency fm, the bandwidth δf, the lower and upper bands f1 and f2.
Then we calculate diffusion coefficients for EMIC waves by using those fitting parameters (Fig. 4). Diffusion coefficients are found to strongly depend on pitch angle and energy. Pitch angle or cross diffusion term can extend to small pitch angles and covers a broad region of pitch angle and energy, whereas momentum diffusion term is confined within a very limited region of pitch angle and energy and drops rapidly when pitch angle decreases to zero. A clear boundary occur for each momentum or cross diffusion coefficient: momentum or cross diffusion coefficients become most pronounced at a few keV within this boundary and decrease sharply outside this boundary. Moreover, pitch angle and cross diffusion coefficients are higher than the momentum diffusion coefficients by a factor of ~ 102 and 10 or above respectively at lower pitch angles, e.g, below 10°, implying that pitch angle diffusion dominates over the energy diffusion while the cross diffusion terms should also contribute to proton-EMIC interaction.
Diffusion rates on 22:48:39 UT (left) and 22:51:37 UT (right).
Proton pitch angle (Dαα, a, d), momentum (Dpp, b, e) and cross (Dαp, c, f) diffusion rates for resonant EMIC wave interactions with cusp protons. (a), (d), pitch angle Dαα or (c), (f), cross Dαp covers a broad region of pitch angle and energy, extending to small pitch angles. (b), (e), Dpp drops rapidly when α decreases to zero, limited within a small region of pitch angle and energy. Combined scattering by all three diffusion rates leads to rapid pitch-angle scattering between 1 and 10 keV at lower pitch angles and the resultant cusp auroral precipitation into the atmosphere on a timescale comparable to a few minutes.
We use those diffusion rates in Figure 4 as input to solve a two-dimensional Fokker-Planck diffusion equation by a recently introduced hybrid difference method13. We calculate PSD evolution of protons due to EMIC waves and then simulate the evolution of differential flux j by the subsequent conversion j = p2f. Since there is currently no data for the variation of the differential flux versus the pitch angle α, we average the flux over the pitch angle with the relation  to compare with the observation. The results (Fig. 5) confirm that the simulation gives an adequate fit to the observed data, i.e., the averaged flux of energetic protons drops with the gyroresonant time very rapidly by a factor of ~ 10 within 6 minutes. We therefore conclude that EMIC waves are indeed responsible for the precipitation of the energetic protons into the atmosphere, leading to the resultant proton aurora.
to compare with the observation. The results (Fig. 5) confirm that the simulation gives an adequate fit to the observed data, i.e., the averaged flux of energetic protons drops with the gyroresonant time very rapidly by a factor of ~ 10 within 6 minutes. We therefore conclude that EMIC waves are indeed responsible for the precipitation of the energetic protons into the atmosphere, leading to the resultant proton aurora.
Evolution of the proton flux due to wave scattering.
Starting with an initial condition representative of protons, we show the averaged flux due to scattering by EMIC waves from a numerical solution to the two-dimensional Fokker-Planck diffusion equation. EMIC causes a remarkable loss of low-energy (6.50 and 10.53 keV) protons, leading to the strongest proton auroral precipitation in the 11:00 MLT sector.
Discussion
The present modelling is the first study to associate EMIC waves with the origin of cusp proton aurora. Our results definitively show that EMIC waves scatter the trapped energetic protons to precipitate into the atmosphere, forming the cusp proton aurora. Considering that the cusp is highly variable in particle density, ambient magnetic field and even cusp locations14, this will potentially change the time scale or amplitude for the proton precipitation but will not change the basic properties of EMIC-proton interaction. Therefore, this conclusion obtained by calculations at a particular time period should be generally valid though the properties of EMIC waves and dynamics in the cusp region are different under different geomagnetic times.
It should be pointed out there are possibly additional mechanisms responsible for generation of the cusp proton aurora. At first, magnetic reconnection is really needed to inject protons into the cusp region. EMIC waves then scatter those trapped protons into the loss cone via wave-particle interaction. Hence, combination of magnetic reconnection and EMIC waves yields the resultant cusp aurora. Secondly, a few percent of protons with initial high parallel velocities may not be trapped and can directly precipitate into the atmosphere, contributing to cusp proton aurora. Finally, electrostatic waves which have not a magnetic field component can also be another generation mechanism. To investigate this, we have examined (not shown for brevity) the electric field data in the period of interest. Unfortunately, there is no realistic wave data in the frequency range from a few Hz to ~ 40 kHz. Only slightly noticeable (or very weak) wave data are observed around 55~65 kHz between 22:40–22:50 UT. Since the proton gyrofrequency is very low ~ 1 Hz in the case of study, it is very hard for the electrostatic wave with such high frequency to efficiently resonant with protons and scatter protons into the loss cone. However, considering that electrostatic wave is very common in the cusp region, the electrostatic wave still possibly produces efficiently scattering of protons during different periods and/or locations. This deserves a further study.
Methods
To calculate the diffusion rates, we assume that EMIC waves propagate along the ambient field line in a simple hydrogen-electron plasma and the wave spectral density  follows a typical Gaussian frequency distribution with a center fm, a half width δf, a band between f1 and f215.
follows a typical Gaussian frequency distribution with a center fm, a half width δf, a band between f1 and f215.

here  is the wave amplitude in units of Tesla and erf is the error function. Diffusion coefficients due to EMIC waves are then computed in the cusp region with the observed magnetic field amplitude of 45 nT and the background proton number density of 30 cm−3.
is the wave amplitude in units of Tesla and erf is the error function. Diffusion coefficients due to EMIC waves are then computed in the cusp region with the observed magnetic field amplitude of 45 nT and the background proton number density of 30 cm−3.
The evolution of the proton phase space density is calculated by solving the pitch angle and momentum diffusion equation

here, p is the proton momentum, α is the pitch angle, Dαα, Dpp and Dαp = Dpα represent diffusion coefficients, respectively, in pitch angle, momentum and cross pitch angle-momentum. The explicit expressions of those local diffusion coefficients for field-aligned propagating EMIC waves can be found in the previous works16,17.
The initial condition is modeled by a kappa-type distribution function of energetic protons18:

here np is the number density of energetic protons, l indicates the loss-cone index, κ represents the spectral index, Γ is the gamma function, θ2 stands for the effective thermal parameter scaled by the proton rest mass energy mpc2 (~938 MeV).
Boundary conditions are chosen as follows. For the pitch angle operator, f = 0 at α = 0 to simulate a rapid precipitation of protons (Fig. 1d) and ∂f/∂α = 0 at α = 90°. For the energy diffusion operator,  (0.1 keV) = const at the lower boundary 0.1 keV and
(0.1 keV) = const at the lower boundary 0.1 keV and  (0.1 MeV) = const at the upper boundary 0.1 MeV based on the observation (Fig. 1c).
(0.1 MeV) = const at the upper boundary 0.1 MeV based on the observation (Fig. 1c).
Based on the observational data we choose the following values of parameters: θ2 = 0.5 × 10−6 (~5 keV), l = 0.01, κ = 3 and np = 4.1 cm−3. The equation is solved using the recently introduced hybrid difference method13. This method is efficient, stable and easily parallel programmed. The numerical grid is 91 × 101 and uniform in pitch angle and natural logarithm of momentum.
References
Smith, M. F. & Lockwood, M. Earth's magnetospheric cusps. Rev. Geophys. 34, 233 (1996).
Fuselier, S. A., Anderson, B. J. & Onsager, T. G. Electron and ion signatures of field line topology at the low-shear magnetopause. J. Geophys. Res. 102, 4847 (1997).
Crooker, N. U. Reverse convection. J. Geophys. Res. 97, 19363–19372 (1992).
Phan, T. et al. Simultaneous Cluster and IMAGE observations of cusp reconnection and auroral proton spot for northward IMF. Geophys. Res. Lett. 30 (2003).
Tsyganenko, N. A. & Stern, D. P. Modeling the global magnetic field of the large-scale Birkeland current system. J. Geophys. Res. 101, 27187–27198 (1996).
Summers, D., Thorne, R. M. & Xiao, F. Relativistic theory of wave-particle resonant diffusion with application to electron acceleration in the magnetosphere. J. Geophys. Res. 103, 20487–20500 (1998).
Grinsted, A., Moore, J. C. & Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 11, 561–566 (2004).
Mende, S. B. et al. Far ultraviolet imaging from the IMAGE spacecraft, 3, Spectral imaging of Lyman-alpha and OI 135.6 nm. Space Sci. Rev. 91, 271 (2000).
Fuselier, S. A. et al. Cusp aurora dependence on interplanetary magnetic field Bz. J. Geophys. Res. 107(A7), 1111 (2002).
Frey, H. U. et al. Proton aurora in the cusp. J. Geophys. Res. 107(A7), 1091 (2002).
Thorne, R. M., Ni, B., Tao, X., Horne, R. B. & Meredith, N. P. Scattering by chorus waves as the dominant cause of diffuse auroral precipitation. Nature 467, 943–946 (2010).
Glauert, S. A. & Horne, R. B. Calculation of pitch angle and energy diffusion coefficients with the PADIE code. J. Geophys. Res. 110, A04206 (2005).
Xiao, F., Su, Z., Zheng, H. & Wang, S. Modeling of outer radiation belt electrons by multidimensional diffusion process. J. Geophys. Res. 114, A03201 (2009).
Dunlop, M. W., Cargill, P. J., Stubbs, T. J. & Woolliams, P. The highaltitude cusps: HEOS2. J. Geophys. Res. 105, 27509 (2000).
Lyons, L. R., Thorne, R. M. & Kennel, C. F. Pitch angle diffusion of radiation belt electrons within the plasmasphere. J. Geophys. Res. 77, 3455–3474 (1972).
Summers, D. Quasi-linear diffusion coefficients for field-aligned electromagnetic waves with applications to the magnetosphere. J. Geophys. Res. 110, A08213 (2005).
Xiao, F., Chen, L., He, Y., Su, Z. & Zheng, H. Modeling for precipitation loss of ring current protons by electromagnetic ion cyclotron waves. J. Atmos. Sol. Terr. Phys. 73, 106 (2011).
Vasyliunas, V. M. A survey of low-energy electrons in the evening sector of the magnetosphere with ogo 1 and ogo 3. J. Geophys. Res. 73(9), 2839–2884 (1968).
Acknowledgements
This work was supported by 973 Program 2012CB825603, the National Natural Science Foundation of China grants 40931053, 40925014, the Aid Program for Science and Technology Innovative Research Team in Higher Educational Institutions of Hunan Province and the Construct Program of the Key Discipline in Hunan Province.
Author information
Authors and Affiliations
Contributions
F.L.X. and Q.G.Z. led the idea and modelling, Z.P.S. and C.Y. contributed modelling, Z.G.H. and Y.F.W. contributed data analysis and interpretation and Z.L.G. contributed plotting Fig. 1.
(Cusp proton aurora and trapped protons).
(upper). Schematic diagram showing the protons trapped in the cusp B-field minimum plane based on T96 magnetic field topology. The black spiral lines represent trajectories of the trapped proton due to the first adiabatic invariant. The blue lines denote the magnetic field lines. The color represents the magnetic strength in nT. Wave-particle interaction occurs around the minimum B position and acts as a potential mechanism to scatter the trapped protons into the atmosphere. (lower). The cusp aurora formed by the protons from the solar wind via magnetic reconnection.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Xiao, F., Zong, Q., Su, Z. et al. Determining the mechanism of cusp proton aurora. Sci Rep 3, 1654 (2013). https://doi.org/10.1038/srep01654
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01654
This article is cited by
-
Generation of proton aurora by magnetosonic waves
Scientific Reports (2014)
-
Effect of chorus normal angle on dynamic evolution of radiation belt energetic electrons
Astrophysics and Space Science (2014)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.