Introduction

When we apply a shear force to a solid object on a solid substrate to start a sliding motion, the shear force must be greater than the maximum static friction force. When the object is sliding, the kinetic friction force applies. Friction plays an important role in various phenomena ranging from those at the nanometre scale to earthquakes; the phenomenon of friction has been investigated since ancient times1,2,3,4,5. From the engineering point of view, friction is required to be small in certain cases and large in other cases. The control of friction is one of the key factors towards achieving improvements in green technology and nanotechnology. In the 15th century da Vinci discovered that the friction force is proportional to the applied loading force and is independent of the apparent contact area between two solid surfaces1,2,3,4,5. This behaviour of friction was rediscovered by Amontons approximately 200 years later; this law is now called Amontons' law of friction and holds for various systems at first approximation1,2,3,4,5. The ratio of the friction force to the loading force is called the friction coefficient and according to Amontons' law, this coefficient does not depend on the loading force or the apparent contact area. The mechanism of friction was explained in the mid-twentieth century by Bowden and Tabor1. For actual solid surfaces in contact with each other, because of surface roughness, only a tiny fraction of the surfaces form junctions, the so-called real contact points. Amontons' law is explained as resulting from the increase in the total area of real contact points, that is, the real contact area, in proportion to the loading force and the constant binding energy per unit real contact area1,2,3,4,5,6,7. However, the mechanism and the validity of Amontons' law are still discussed actively2,3,4,5,6,7,8,9,10,11,12,13.

Another interesting problem concerning sliding friction is the question of how a macroscopic object begins to slide. Usually, it is considered that a shear force smaller than the maximum static friction force does not induce any slip motions. However, recent measurements of the instantaneous local real contact area density of poly-(methyl methacrylate) (PMMA) show that precursors appear as local slips at the interface under shear forces well below the maximum static friction force and this force corresponds to the onset of bulk sliding14,15,16,17. If the shear force is applied slowly from the trailing edge of the sample, a discrete propagation sequence for the local slip appears15. Each front of the slip starts from the trailing edge and stops after propagating a certain length greater than that of the previous front. When the slip front reaches the leading edge, bulk sliding occurs. Similar behaviour is observed in numerical studies based on 1D17,18,19,20 and 2D21 spring-block models. The variation in the front velocity and the front velocity's dependence on the stress distribution have been observed in experiments14,16 and have been examined using numerical approaches18,21,22. A slow precursor with a finite front velocity has been investigated with a 1D continuum model23,24. The precursor dynamics are expected to relate to the inhomogeneity of the system and are expected to be important to the understanding of friction. In fact, ref. 9 reported that the macroscopic static friction coefficient μM, which corresponds to the maximum static friction force, varies with the experimental loading configuration and this variation is related to the precursor dynamics. Similar behaviour for the maximum static friction force has also been investigated with a 1D spring-block model25. Despite these studies, however, the mechanism of the precursor and its relation to the maximum static friction force have not been clarified theoretically.

In this study, using both numerical and analytical methods, we investigate the precursor dynamics and the relation of these dynamics to the macroscopic static friction coefficient μM of an elastic object in contact with a rigid substrate and we show that μM decreases as pressure or system length increases. This behaviour indicates the systematic breakdown of Amontons' law. In the present system, the elastic object is subject to viscous damping and a friction force that obeys Amontons' law locally; however, the law breaks down for the overall system. The breakdown of the law results from a quasi-static precursor appearing in the propagation of local slips before the onset of bulk sliding and from the transition of the quasi-static precursor to a dynamic precursor at a certain critical precursor length. For sufficiently large or small pressures or system lengths, μM becomes nearly constant and Amontons' law approximately holds. The relation of μM to the critical precursor length and the mechanism of the breakdown are clarified analytically with a 1D effective model. These behaviours arise from the distribution of pressure on the bottom of the object, which results from the torque induced by the shear force and from the competition between the viscous damping and the velocity-weakening friction. Consequently, the behaviours do not depend on the details of the system. It is known that Amontons' law does not apply under some conditions, such as in the presence of strong adhesion, in the absence of multiple real contact points, with nonlinear dependence of the real contact area on the applied load, with surface detachment, with a change in surface conditions and for gels2,3,4,6,10,11. However, the mechanism of the breakdown of Amontons' law discussed in this paper is different from those known previously. In addition, a theoretical prediction of the behaviour of the friction coefficient is given for the first time. These results will provide new approaches to control friction.

Results

Finite element method (FEM) calculation

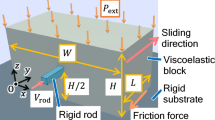
We first analyse the friction behaviour for an elastic block with length L, width W and height H along the x-, y- and z-axes, respectively, on a rigid substrate (see Fig. 1(a)) using a 2D finite element method (FEM). We assume that the block has viscous damping proportional to the strain rate and has friction stress proportional to the pressure at the interface; that is, the local friction force obeys Amontons' law. Note that the resolution of the models employed in this work is larger than the mean distance between the real contact points between the two surfaces and smaller than the length scale of the variation of the stresses discussed below. The validity of the law on this length scale for PMMA is supported by the proportionality of the real contact area to the loading pressure7, with the assumption of a constant binding energy per unit real contact area and the law's validity is consistent with the friction experiments in which the size of the apparent contact area is on the order of 1 mm2 in a multiple real contact point configuration6. The local friction coefficient is given by the local static friction coefficient μS when the local slip velocity is equal to zero and it decreases linearly from μS to the local kinetic friction coefficient μK with increasing until the local friction coefficient finally equals μK at velocities greater than characteristic velocity vc. The plane stress condition is assumed along the y-axis. We apply a uniform pressure Pext = FN/(LW) to the top surface, where FN denotes the loading force. The shear force FT is applied from the trailing edge at height h by means of a rigid rod with a width of 0.1H. The rod moves with a constant velocity V that is sufficiently slow. We set W = 1 and h = H/2. The results shown here do not depend on the details of the system parameters. However, for the quantitative calculations, we employ two parameter sets; parameter set (A) simulates a model viscoelastic material and (B) simulates PMMA. Hereafter, we employ quantities normalised by the mass density, Young's modulus and viscosity and these quantities are expressed with a tilde. The following results are obtained for . (See Methods for more details regarding the FEM calculation, the velocity dependence of the local friction coefficient and the parameters.).

Figure 1
figure 1

(a) An elastic object under uniform pressure Pext = FN/(LW) on a rigid substrate is pushed at height h by a rigid rod with shear force FT.(b) The ratio as a function of . The horizontal line indicates the value of μM. The inset shows an enlarged view of the box indicated by the red outlines. (c) The local slip region is shown in red in the plane. The horizontal line indicates the critical length of the quasi-static precursor . (d) The normalised instantaneous local density of the real contact area in the region of the box indicated by blue outlines in (c). The thin line indicates the position of the precursor front. The results are obtained for , and parameter set (A).

Full size image

Figure 1(b) shows the ratio as a function of the displacement of the rod , where denotes time. The ratio repeatedly shows a nearly linear increase and a periodic large drop after the first drop. In this work, we focus on the periodic regime. The periodic behaviour corresponds to a periodic stick-slip motion. The large drop is caused by a large slip accompanied by bulk sliding. The value of at the peak of the curve is the maximum static friction force. The inset shows an enlarged view of the box indicated by the red outline. A sequence of small drops in is clearly observed before the onset of bulk sliding at . As discussed below, each small drop is accompanied by a rapid local slip. This behaviour has previously been observed in certain experiments15 and numerical studies17,18,19,20,21. Figure 1(c) shows the local slip region, where the slip velocity at the interface has a finite value, in the plane. Here, denotes the position at the bottom of the object. At values well below the maximum static friction force, the shear force induces a slow precursor slip from the trailing edge and this precursor slip is called the quasi-static precursor. The velocities of the local slip and the front of this precursor are proportional to the driving velocity and they are vanishingly small. The precursor length increases with increasing . When reaches a critical length , the quasi-static precursor becomes unstable and transforms to a leading rapid precursor with large slip and front velocities. The leading rapid precursor nucleates near the trailing edge. The front of the leading rapid precursor begins with a velocity close to that of sound and in a manner similar to the supershear rupture observed in experiments9,16. Subsequently, the front velocity reduces and approaches the Rayleigh wave velocity. When the front enters the leading edge, bulk sliding occurs and FT shows a large drop in value.

Figure 1(d) shows the normalised instantaneous local density of the real contact area in the region of the box indicated in (c). The local density is calculated from the local slip velocity and decreases with increasing velocity. (See Methods for this calculation.). Before the onset of bulk sliding at , a discrete sequence of rapid precursors, similar to that observed in experiments15, appears at and this set of precursors causes the sequence of small drops in observed in the inset of (b). This type of precursor is called the bounded rapid precursor. Each precursor nucleates in the region with a front velocity that is close to the velocity of sound and is independent of the driving velocity and nucleates in a manner similar to the leading rapid precursor. Subsequently, the front decelerates and stops after propagating a certain length. The propagation length of the precursor front increases with . This increase is also observed in experiments15. The local slip velocity of this precursor is considerably larger than that of the quasi-static precursor shown in (c); however, this slip velocity decreases with decreasing driving velocity in contrast to the behaviour of the slip velocity for the leading rapid precursor. The quasistatic precursor observed in (c) almost disappears for the real contact area density shown in (d) because of its vanishingly small slip velocity. The disappearance of the quasi-static precursor is also consistent with the results of certain experiments15.

We define the macroscopic static friction coefficient μM to be the peak value of in Fig. 1(b). The pressure dependence of μM is shown for various values of the system length in Figs. 2(a) and 2(b) for parameter sets (A) and (B), respectively. Clear decreases in μM are observed with increasing or values. It can be shown that μM also depends on the apparent contact area. These behaviours indicate the breakdown of Amontons' law and the extensive property of the friction force. This pressure dependence is consistent with the results of experiments conducted with PMMA8,9. The magnitudes of the normalised parameters, and , depend on the mass density, Young's modulus and the viscosity coefficient. Therefore, in contrast to the general belief that the friction coefficient depends mainly on the surface properties, μM also depends on these bulk material parameters, as noted in ref. 25. The variation in μM results from the formation of the precursors before the onset of bulk sliding. Figure 3(a) shows that μM is scaled by the critical length of the quasi-static precursor normalised by the system length, , for each parameter set. The dependence of on , shown in the inset, with this scaling of μM on indicates the dependence of μM.

Figure 2
figure 2

Macroscopic static friction coefficient μM as a function of for parameter sets (A) (a) and (B) (b).

The lines with symbols indicate the results of the FEM calculation. Thin lines indicate analytical results based on the 1D effective model, where we set α = 0.2. Lines of the same colour correspond to the same value of .

Full size image
Figure 3
figure 3

(a) Macroscopic static friction coefficient μM as a function of for various values of and .The open symbols indicate results for the parameter set (A) with (), 1.0 () and 4.0 () and the filled symbols indicate those for (B) with (), 0.04 () and 0.08 (). The lines show the theoretical result as obtained with equation (2). The inset shows the dependence of for parameter set (A). (b) The normalised pressure and (c) the ratio of the shear stress to the pressure at the interface for the magnitudes of indicated by arrows in Figs. 1(b) and 1(c). The arrows in (c) indicate the positions of the precursor front. The three horizontal lines μS, μM and μK in order from the top of the panel. The parameters are the same as those for Figs. 1(b–d).

Full size image

Figure 3(b) shows the pressure at the interface for the magnitudes of indicated by arrows in Figs. 1(b, c). The applied pressure at the top surface is uniform; however, is not uniform and increases with . Similar pressure distributions are observed in experiments9,16 and result from the torque induced by the shear force 19. The low pressure causes the local maximum static friction force to be small. As a result, the quasi-static precursor starts from the trailing edge at . Figure 3(c) shows the ratio of the shear stress at the interface to the pressure, . Immediately after bulk sliding stops, this ratio approximately equals the value of μK (dashed line) for the entire interface because of the large local slip velocity accompanied by the bulk sliding and the finite relaxation time of the local stress. The magnitude of is equal to the local friction stress at the instant of the vanishing acceleration of the rapid local slip and this magnitude has almost no change during the deceleration and after stoppage because of the finite relaxation time. However, in the region of length where the quasi-static precursor front has passed, equals μS (straight line) because is given by the local friction stress for vanishing velocity . When reaches the critical length , the quasi-static precursor transforms to the leading rapid precursor. Subsequently, the front of this rapid precursor enters the leading edge of the system quickly and bulk sliding occurs. The stress distribution has almost no change during the propagation of this front because of the short duration of the propagation. As a result, μM is determined by and this relation is shown analytically below. Note that the stress relaxes slightly after the appearance of each of the bounded rapid precursors and the stress recovers its original value quickly through the following quasi-static precursor, as shown in Fig. 1(d). Figure 3(c) also shows that can be larger than the macroscopic static friction coefficient μM without precipitating any local slip, as was observed in experiments9,16.

Analysis based on a 1D effective model

To analyse the abovementioned numerical results, we employ a 1D effective model in which the degrees of freedom of the elastic object along the z-axis are neglected. The equation of motion of the model is expressed by

Here, denotes the displacement along the x-axis at the interface, is the friction stress and denotes the characteristic length of the variation in the (xz) component of the stress. We employ α as a fitting parameter. The normal and the shear stresses are respectively given by and , where denotes the effective viscosity and and represent effective elastic constants (see Methods for these parameters and the boundary condition.). We assume that the pressure at the interface is given by , which simulates the FEM result shown in Fig. 3(b). Hereafter, we set the origin of to be the position of the pushing rod just after bulk sliding stops. The adiabatic solution of equation (1) with a precursor of length is obtained analytically and the solution gives for (see Supplementary Information). Hence, increases adiabatically with an adiabatic increase in . This adiabatic increase in length indicates the precursor is quasi-static. A similar relation between the precursor length and the shear force is obtained with a 1D spring-block model; however, in this case the precursor is not adiabatic20. When reaches a critical length , the quasi-static precursor becomes unstable and transforms to the leading rapid precursor. The leading rapid precursor leads to bulk sliding. Substituting the adiabatic equation and the relation between and into the expression for the shear force and setting , we obtain

for . As shown in Fig. 3(a), this relation agrees well with the FEM calculation, even for .

The critical length is obtained by a linear stability analysis of equation (1) in the limit of vanishing (see Supplementary Information). The analysis provides the equation for the n-th eigenvalue of the time evolution operator for the fluctuation by

where , and . Here, the off-diagonal terms, which are of a higher order in , are neglected. The eigenvalue gives the instability condition of the adiabatic solution. The instability results from the appearance of a positive real part for any eigenvalue. For small values of , the viscosity expressed by the second term in equation (3) stabilises the adiabatic motion. However, the velocity-weakening friction force expressed by the last term leads to instability in motion for large . In the present case, the oscillating fluctuation corresponding to a complex with a positive real part never grows, because the backward motion of the oscillation relaxes the local shear stress and this motion is inhibited by the friction stress. Instead, this oscillating fluctuation yields the bounded rapid precursors observed in Fig. 1(d).

The appearance of the positive real part of at , where denotes the subcritical length, yields the first bounded rapid precursor and the appearance of with n ≥ 1 is considered to yield each of the subsequent precursors appearing at . Further increase in causes to become real and positive at ; a positive, real results in the growing instability and causes the leading rapid precursor and the subsequent bulk sliding. The relation between and is given by the instability condition, . As mentioned above, the instability is caused by the competition between the viscosity and the velocity-weakening friction force, which are expressed by the second and last terms in equation (3), respectively. Hence, decreases as or increases because the last term is enhanced by ; for , as is easily seen from equation (3) (also see Supplementary Information). This result is consistent with that of the FEM calculation shown in the inset of Fig. 3(a). By inserting , which is given by the abovementioned relation, into equation (2), we obtain the pressure and system length dependence of μM and μM decreases with increasing or . The results are shown in Figs. 2(a,b). The analytical results agree with the FEM calculation semiquantitatively for parameter set (A) and qualitatively for parameter set (B). The deviation of the analytical results from the FEM calculation may arise from the absence of internal degrees of freedom along the z-axis in the 1D effective model given by equation (1).

Discussion

In this work we observed three types of precursors prior to the occurrence of bulk sliding: the quasi-static precursor and the bounded and the leading rapid precursors. The latter two are seen to correspond to those observed in experiments9,14,15,16,17. The quasi-static precursor is also observed in numerical studies23, but not in experiments9,14,15,16,17, because it vanishes away in the local density of the real contact area measured in experiments, as previously discussed. Some numerical studies17,19,20,21 do not report this precursor. The lack of this precursor is because local friction coefficient discontinuously decreases as velocity increases in these studies. This discontinuous decrease in the local friction coefficient corresponds to a vanishing vc and a subsequently vanishing stable region for the quasi-static precursor. In ref. 22, a model similar to the present FEM model is employed; however, the value of the viscosity coefficient corresponds to . This result is also consistent with the absence of the quasi-static precursor.

In ref. 9, it was reported that μM varies with a certain acceleration length of the leading rapid precursor. The acceleration length is difficult to define in the present work and this difficulty may result from a loading configuration different from that of the experiment. The relation of μM with the acceleration length will be studied in future work. However, the measured values of μM in ref. 9 show a tendency to decrease with an increase in the loading force and depend on the stress distribution in the system. These behaviours are consistent with those observed in the present work.

Earthquakes are among the largest friction phenomena on the earth. Many large earthquakes are preceded by foreshocks. In the 2011 Tohoku-Oki earthquake with magnitude 9, the propagation of slow slip preceding the main shock was observed over approximately 1 month26. The behaviour is similar to the propagation of the precursor front observed in this work. The present results will provide new insights into earthquake behaviour.

In conclusion, using both numerical and analytical methods, we show that the macroscopic static friction coefficient μM of an elastic object decreases with increasing pressure or system length. The magnitude of μM also depends on the apparent contact area and the bulk material parameters. These behaviours indicate the systematic breakdown of Amontons' law. The elastic object is subject to viscous damping and a friction force that obeys Amontons' law locally; however, the law undergoes breakdown as a whole. The behaviour of μM is consistent with the results of relevant experiments8,9 and it arises from the occurrence of precursor slips before bulk sliding and from the transition from quasi-static to rapid motion of the precursors. The linear stability analysis based on a 1D effective model gives the relation between μM and the critical length of the transition and it clarifies the mechanism of the transition. The transition is caused by the pressure distribution at the bottom of the object, which results from the torque induced by the shear force and by the competition between the viscous damping and the velocity-weakening friction. If the ratio of the critical length of the transition to the system length is considerably less than or approximately equal to unity, μM becomes almost constant and Amontons' law holds approximately. These situations are caused by sufficiently large or small values of pressure or system length. The qualitative features of these results do not depend on the details of the model for the case in which the pressure at the bottom of the object increases monotonically along the driving direction, the local friction coefficient decreases with velocity continuously and the system has viscous damping. According to these results, an object with greater width or an object in which the part contacting with the interface is divided into shorter portions along the driving direction can have a larger maximum static friction force under a constant loading force. The present results will provide new techniques for controlling friction.

Methods

FEM calculation

The equation of motion of the displacement vector of the elastic object u(r, t) employed in the FEM calculation is expressed as , where ρ is the mass density. The stress tensor σ is composed of an elastic part σ(el) and a dissipative part. The dissipative component is expressed as . Here denotes a component of the strain rate tensor and η1,2 denote the viscosity coefficients27. The boundary condition is given by σzz = −Pext and σxz = 0 at the top surface and σxx = 0 and σzx = 0 at x = 0 and L except for the portion in contact with the rigid rod.

In the FEM calculation, the object is divided into equal-sized rectangular cells. The number of cells is 40 × 40 or 80 × 80. The convergence of the results with respect to the FEM mesh size is verified. At the beginning of the FEM simulation, we apply a uniform pressure to the top surface causing the elastic object to relax. Subsequently, we start pushing the object at . The results shown in the paper are obtained for . This value of corresponds to the adiabatic limit except for the results shown in the inset of Fig. 1 (b) and in Fig. 1 (d).

Velocity dependence of the local friction coefficient and the real contact area density

The velocity dependence of the local friction coefficient employed in this work is obtained from the rate- and state-dependent friction law, μ = μK + (μS − μK)ϕ with , as discussed in ref. 4. Here, 0 ≤ ϕ ≤ 1 represents the state variable and τ and D denote the relaxation time and length, respectively. The above equation yields , as noted in the text for vc = D/τ, in the limit of vanishing τ, where . The magnitude of ϕ is proportional to the deviation of the local density of the real contact area from that for . Thus, we obtain the normalised instantaneous local density of the real contact area shown in Fig. 1(d).

Parameters

We introduce the normalised quantities in which the length, mass and time are normalised by , and , respectively, where E represents Young's modulus. In this paper, the normalised quantities are expressed with a tilde. We employ two parameter sets: parameter set (A) simulates a model viscoelastic material, which has Poisson's ratio ν = 0.34, μS = 0.38, μK = 0.1, and ; and (B) simulates PMMA, which has ν = 0.4, μS = 1.2, μK = 0.2, and . The present FEM calculation shows that μS and μK correspond to the maximum and minimum values of the ratio of the local shear stress to the pressure, respectively. Hence we estimate μS and μK for PMMA from the maximum value of the ratio in Fig. 4(c) and the minimum value of the ratio in Fig. 4(b) in ref. 9, respectively. The value of vc is estimated from the values of μS, μK and the linear fit of the steady-state velocity dependence of the rate- and state-dependent friction law reported in ref. 5. The value of L0 for PMMA is estimated as follows. In ref. 9, μM = 0.6 for L = 0.2 m, d = 0.5 and Pext = 1.67 × 106 Pa. The FEM calculation yields μM = 0.6 for . Consequently, we obtain L0 = 48 m. These values of the parameters for PMMA have some uncertainties. However, the essential feature of the results obtained here is, as mentioned before, not specific to these values. The local validity of Amontons' law for PMMA may require some discussions. Even if Amontons' law breaks down locally, the behaviour of the precursor dynamics and the static friction force discussed here will be still qualitatively valid because their mechanism is general. For metals, Amontons' law is expected to better hold locally and the present qualitative results will also be applicable.

1D effective model

In the 1D effective model, the effective viscosity is given by and the two elastic constants are given by and . The boundary condition is given by at and .