Introduction

Generally, crystalline sp2 carbon materials (except fullerenes) such as carbon nanotubes and graphene have much better electrical conductivity than amorphous carbon materials, but have rather limited specific surface area (SSA) in bulk states in spite of their high theoretical SSA1. This is contrary to the bulk amorphous sp2 carbon materials such as activated carbon (AC), which have much lower conductivity but higher SSA. So the question is that if there is a way to build such carbon materials with both high SSA and conductivity in the bulk state? Obviously, such materials, if prepared in a facile and cost-effective way, shall have significant implications for both academic and industry communities, for example, employed as the electrode materials for the increasing important energy storage/conversion device applications1.

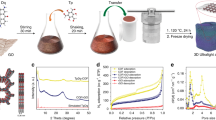
Here we introduce such a simple and green but very efficient and industrially scalable approach (Fig. 1a) using two standard industry steps including: 1) in-situ hydrothermal polymerization/carbonization of the mixture of cheap biomass or industry carbon sources with graphene oxide (GO) to firstly get the 3D hybrid precursor materials and then 2) a chemical activation step to achieve the desired SSA and conductivity. It is important to note that the carbon atom yield is almost 100% from the first step2, which is a significant and important improvement compared to the conventional direct carbonization process used in industry due to both the cost and environmental issues3. And both steps are very industrially scalable and efficient to make truly large quantity of products2,4. Various structural and morphology analyses demonstrate that these materials consist of almost entirely defected/wrinkled single layer graphene sheets in the dimensional size of a few nanometers, with ultrahigh SSA (up to 3523 m2/g) and excellent bulk conductivity (up to 303 S/m). The pore size of these materials mainly distributes in the mesopore size range, significantly different from the conventional AC materials5,6. These combined outstanding properties make them superior candidate materials for various applications, as demonstrated by their so far the best supercapacitor performance.

Figure 1
figure 1

(a) A schematic show of the simple and green process of synthesizing porous 3D graphene-based materials.(b) Low magnification and (c) high-resolution scanning electron microscopy (SEM) images of products from the mixtures of PF and GO with optimized ratios, which exhibited sponge-like morphology and porous structure. (d) Low magnification and (e) high-resolution transmission electron microscopy (TEM) images of products from the mixtures of PF and GO with optimized ratios, which also showed a dense 3D pore structure with highly curved or wrinkled surface.

Full size image

Results

Synthesis of 3D porous graphene-based materials

We firstly tested our idea using the mixture of water soluble, cheap basic industry material sucrose and GO. A series of products (Supplementary Table S1) denoted as SU8G-HA, SU16G-HA, SU24G-HA and SU32G-HA have been prepared with different ratios of sucrose/GO, where the numbers represent the feed ratio of sucrose/GO (see Supplementary Information for details). For comparison, SU-HA and G-HA were also prepared with the same process from pure sucrose and GO, respectively. Indeed, the products obtained through these two simple steps exhibit both ultrahigh SSA and good conductivity, with the best values reaching up to 3355 m2/g and 77 S/m for the optimized product SU24G-HA prepared from mixture of sucrose and only ~4 wt.% addition of GO. In the contrary, the products derived from pure sucrose or GO exhibit significantly lower SSA. The SSA of optimized product is much higher than that (1739 m2/g) of one of the most used high end industry AC products, RP207. And the conductivities of these products (~102 S/m) are not only about two orders higher than that of RP20 (~5 S/m) at the pristine state and even significantly higher than that (~47 S/m) of RP20 mixed with 10% of conductive carbon black (CB). The conductivity of our products also increases with more GO addition as expected, indicating a great role of graphene for the improvement of electrical conductivity. More detailed discussion about this will be presented below in the morphology and structural analysis. Similar products were prepared from other two commercially most available biomass materials, cellulose and lignin. With the same simple process, surprisingly, all of them gave very similar properties as those from sucrose/GO (Supplementary Table S2).

Some of the cheap industry polymer materials have also been widely studied and used to prepare AC materials2 and one of the typical polymers is phenolic resin8. So next, we used the simple mixture of phenol (P) and formaldehyde (F) as the carbon source (denoted as “PF”) and followed the same procedure as above to obtain the PF/GO products with different PF/GO ratios. The obtained products also exhibit excellent results for both SSA and conductivity (Supplementary Table S3). For example, product PF16G-HA, in which the weight ratio of PF/GO is 16, gave a SSA of 3523 m2/g and conductivity of 303 S/m, respectively. To further test the applicability of our method, another widely used and low-cost polymer polyvinyl alcohol (PVA) was tested in the similar way with different ratios of PVA/GO. The optimized product PVA20G-HA (the weight ratio of PVA/GO is 20) also exhibits similar and excellent performance with both high SSA (3192 m2/g) and conductivity (67 S/m) (Supplementary Table S4). Table 1 has summarized all the results for the products from the optimized carbon source/GO ratios, which all give similarly ultrahigh SSA and excellent conductivity. These results indicate that our approach can be applied to a wide range of biomass and polymer carbon source materials and generate bulk porous materials at industry scale with both ultrahigh SSA and excellent conductivity with the addition of only a few percent of GO.

Table 1 SSA and conductivity of all the 3D graphene-based products from the mixtures of GO and various cheap carbon sources. “PF”, “PVA”, “SU”, “CE” and “LI” are short names to represent the corresponding carbon sources of (phenol + formaldehyde), polyvinyl alcohol, sucrose, cellulose and lignin, respectively. All the experimental values presented are the averaged values and the statistical deviation is about ±5%
Full size table

Morphology and structural analysis

As mentioned above, the ratios of carbon source to GO have great impact for both the conductivity and SSA (Supplementary Table S1-S4). In all cases, when only the carbon source or GO is used, the SSA is much lower. The products prepared from carbon source/GO mixtures always have better conductivity which increase with the ratios of GO/carbon source, indicating the key role played by the addition of GO. Due to the excellent molecular-level dispersion at the very beginning9 and the nature of the two reaction steps, the added graphene sheets should have been distributed homogeneously in the whole carbon matrix and work as a conducting filler to enhance the overall conductivity. Only a small amount of the filler is needed to achieve the required percolation and high conductivity. This is similar to the composites with low percolation values where molecular level distribution of conducting fillers is achieved in the matrix10.

To achieve both high SSA and conductivity, there is an optimized ratio for the carbon source/GO, which is not always the same for different carbon sources. Why can a few percent of GO in the starting materials make so much difference? This is because the added graphene sheets from GO leads to significant structural difference of the intermediate products at the first step (Supplementary Fig. S1). When small amount of GO was added, the added graphene sheets from GO could block the stacking of the AC precursor generated from the matrix carbon sources and thus thinner and smaller AC particles are formed with more pores in the next activation step. As shown in Figs. 1b–d, the products with the optimized ratio show sponge-like morphology and porous structure, significantly different from the rather firm/solid structure derived from pure carbon source (Supplementary Fig. S2h). When more GO is added, the chance of graphene sheet stacking from the added GO increases, which in turns has negative effect on the SSA11. Due to the exceptional amount of data in this work, in the following, we will focus our discussion on the products from the optimized ratios.

With both exceptionally high SSA and excellent conductivity for these easily-made and cheap materials, the reasons behind this need to be fully understood. Moreover, so far it is still not fully understood for the structure and the origin of high SSA of bulk sp2 carbon based amorphous materials including AC. In the past, several controversial theories (such as edge and negative surface structure contributions) have been proposed for why AC or graphene materials can have larger SSA than the theoretical SSA (2675 m2/g) of graphene12,13,14. Thus, a comprehensive structure and morphology analysis have been carried out to address this issue.

The element analyses (EA) show that all our products consist of ~93–97 wt.% carbon, ~0.5–0.9 wt.% H and ~2–5 wt.% O (Supplementary Table S5), indicating very few percent of hydrogen or oxygen containing groups. X-ray photoelectron spectroscopy (XPS) analysis further indicates that most of the carbon atoms are sp2 carbons, demonstrated by the overwhelming strong peak at ~284.4 eV in the C1s XPS spectra15,16 (Supplementary Fig. S3). Further quantitative analysis about the carbon hybridization state comes from the Electron Energy Loss Spectroscopy (EELS) analysis17. Compared to graphite, the fraction of sp2 carbon atoms in the optimized products is about 94–96% (assuming graphite to be 100% sp2 carbon, with ±2% error) (Supplementary Fig. S4). This result indicates there is little other carbon hybridization state, such as sp3 or sp carbon.

Knowing that almost all the carbon atoms exist as sp2 carbons (conjugated C = C), we now need to understand how these sp2 carbon atoms or its most stable and basic unit six-membered (benzene) rings are structured and connected together. In the scanning tunneling microscope (STM) image (Supplementary Fig. S5), the basic benzene unit and the lattice structure of graphene sheets (referred as “graphene domains” below as being differentiating from the conventional “graphene” term) are clearly seen18. The next question to be answered is how these graphene domains are connected and packed to form AC.

X-ray diffraction (XRD) and Raman spectra have historically played important roles in the structural characterization of carbon materials19 and were also used to estimate the size and thickness of the graphene domains in sp2 carbon materials20,21. Firstly, compared with XRD results of graphite and products prepared from pure carbon sources, the optimized products from different carbon sources all exhibit a very weak (~1/100 intensity of graphite) and extremely broad (002) peak in the range of 15°–25° (Supplementary Fig. S6), indicating a much more disordered structure and almost no graphene domains stacking exist22. Secondly, the average layer thickness could be further estimated from the XRD lattice parameters23,24. The average domain's height (Lc) can be approximately determined to be 0.7–0.8 nm by using the Scherrer's equation25 (Supplementary Table S6), which is close to the thickness obtained from a typical atomic force microscope (AFM) image for our materials (Supplementary Fig. S7a) and also much smaller than those of products prepared from pure carbon source (~1.28 nm) or pure GO (~1.56 nm). Moreover, there have been reports using Raman to estimate the size of the graphene domains in sp2 carbon materials26,27. Thus, the integrated intensity ratio ID/IG for the D and G bands in Raman is used to roughly estimate the average size (La, in-plane size) of the graphene domains. Based on this, we found that the approximate dimensional size of the optimized products is around 4–6 nm with some changes depending on different starting materials (Supplementary Fig. S8), which is also consistent with the size of graphene domains from the AFM characterization (Supplementary Fig. S7b) and much smaller than those of products prepared from pure carbon source (~9.7 nm) or pure GO (~11.9 nm). It is well known that the thickness of individual single layer graphene sheet from mechanical exfoliation and CVD methods is ~0.4 nm28 and that for GO is the range of ~0.8–1.2 nm29,30. Considering the graphene sheets in our products should mostly exist in more seriously wrinkled and ridged and even folded states, which is supported by the HR-TEM images31,32 (Fig. 1e and Supplementary Fig. S9), we believe that all these data suggest that the basic structure units in our optimized products are small highly defected (wrinkled and/or twisted) graphene sheets in the size of a few nanometers and most of which should be single-layer graphene sheets with likely some few-layer sheets. While it is hard to see clearly how these graphene domains are connected or stacked at next level, it can be concluded that among these sheets, there is almost no long-range structure ordering or best an extremely weak long-range order (in the Z direction). In the contrast, the products prepared from pure carbon source or GO have both larger and thicker (multi-layered) graphene domains and more ordered long-range packing than the optimized products, which result in a much lower SSA as we will discuss below.

Structural modeling for their ultrahigh SSA

Next question is whether this model matches their observed properties such as ultrahigh SSA. Therefore, we carried a series of modeling for various structures using defined graphene sheets with different size and thickness (layers) as the building blocks to calculate the theoretical SSA, which were obtained using a Monte Carlo integration technique where the probe molecule is “rolled” over the framework surface33,34. The details for the modeling are described in the Supplementary Information.

First, with single layer, as shown in Fig. 2a, the calculated results show that the accessible solvent (N2) SSA of graphene domains are significantly higher than the infinite ideal graphene sheet (2675 m2/g) and increase remarkably with the decrease of graphene domain size, which means that when the graphene domains are small, significant contribution for the SSA comes from the edge part35. This is the critical factor of breaking through the theoretical upper limit of the SSA for graphene. As an extreme case for the impact of edge portion to the SSA, benzene ring gives a calculated SSA of 875 m2/g when not considering its edge part, while with the consideration of its edge, the SSA reaches up to 26000 m2/g36, indicating the overwhelming contribution of the edge when the graphene sheets get smaller. Similar results have also been found for larger aromatic systems36. Therefore, if assuming the dimensional size of graphene domains are mostly in the range of 4–6 nm and in single-layer state as indicated above, the corresponding calculated SSA are roughly in the range of 3600–3900 m2/g (Fig. 2a), with the corresponding edge/total carbon ratios in the range of 7–10%. This modeled SSA is in line with our experimental SSA data (3200–3500 m2/g, Table 1). Second, stacking of graphene sheets greatly reduces the SSA. With the same sheet size, the SSA values decrease dramatically with more layers for the graphene domains as shown in Fig. 2b. These results are consistent with earlier modeling results13. For example, for the same size of graphene domains in the range of 4–6 nm, their SSA goes down dramatically from 3600–3900 m2/g to 2081–2243 m2/g when the number of layers increases from one to two. Another possible defect structure is the existence of damaged holes on the main graphene plane in the real graphene materials. Modeling results give the same conclusion (Supplementary Fig. S10).

Figure 2
figure 2

Structure modeling and the calculated SSA.

All the graphene domain models were designed as foursquare plane including armchair and zigzag sides for convenience. The models represent graphene domains with different size and the total carbon atoms: G3: 3.2666 × 3.1980 nm2, 432 C; G4: 4.1188 × 4.1820 nm2, 700 C; G5: 4.9710 × 5.1660 nm2, 1032 C; G6: 6.2492 × 6.1500 nm2, 1530 C; G7: 7.1014 × 7.1340 nm2, 2006 C; G8: 7.9536 × 8.1180 nm2, 2546 C. (a) The accessible solvent (N2) SSA of single layer graphene domains with different dimensional size and edge carbon percent. The accessible solvent (N2) SSA of graphene domains are significantly higher than the infinite ideal/infinite graphene sheet (2675 m2/g) and increase remarkably with the decrease of graphene domain size, which means that when the graphene domains are small, significant contribution for the SSA comes from the edge part. (b) The accessible solvent (N2) SSA of graphene stacking domains with different stacking layer number. The layer spacing of graphene stacking domains was set to 0.4 nm. With the same sheet size, the SSA values decrease dramatically with more stacking layers for the graphene domains.

Full size image

In addition to the intrinsic wrinkling of the graphene sheets as has been observed in many reports37,38, the graphene domains in our products could also be expected to be curved in practice, which can be caused by the existence of pentagons and/or heptagons39 as in the Schwarzite model12 and/or mechanical folding38. The modeling results also indicate that the tortuosity caused by those graphene curvatures will actually reduce the accessible solvent SSA14 (Supplementary Fig. S11).

So one conclusion we can draw is that the ultrahigh SSA of our materials cannot be due to the pentagon and/or heptagon, neither from folded structure or negative curvature caused by (Schwarz Model) structures12,40. Rather, the observed ultrahigh SSA over limit of 2675 m2/g should mainly come from the edge (or defects) of the graphene sheets which also should have the dimensional size of a few nanometers. Overall, in order to prepare sp2 carbon materials with ultrahigh SSA, the graphene domain size must be small (in a single digit of nanometers) and more importantly exists mostly as single-layer state. We believe this should be also applicable to other sp2 carbon materials with high SSA13.

Thus, from these analyses and modeling, the graphene domains in our products should be mostly as single-layered graphene domains in the size of several nanometers and the ratio of edge carbon/total carbon is ~7–10%. The total number of the carbon atoms in each of such graphene domains is in the range of high hundreds to low thousands. It should be noted that such large polyaromatic molecules (or graphene domains) are quite stable even with some defect sites41. Obviously, in terms of chemical bonding, all the geometric edge carbon atoms (whether at the perimeter of each flake or at holes inside the graphene 2D plane; see models in Supplementary Figs. S10a and S10c) must exist as one of the following four terminated states with37: 1) H atoms; 2) dangling bond but without unpaired electron (armchair); 3) dangling bond but with unpaired electrons (zig-zag); 4) O (assume no any other elements exist as practically it is the case). From the EA above, we know that the atom ratio of H/O is roughly 4–6 (Supplementary Table S5). So for a rough and easier estimation, let's ignore O or any other atoms. For the states with unpaired electrons, there have been many reports for both qualitative and quantitative analysis using electron paramagnetic resonance (EPR)42. The carbon terminated with H could be calculated with H wt.% from the EA. Therefore, although we could not know the exact distribution among these four types of edged carbons, which will probably vary for different products, there should be a relationship between the SSA with the hydrogen weight percent and EPR intensity (corresponding to the unpaired electron density). Supplementary Figs. S12 and S13 indeed show that such a strong relationship exists, where the measured SSA increases when the product exhibits higher hydrogen weight percent (H wt.%) and/or more intense EPR signal.

To summarize briefly all the above structural results, we can see that the results from XRD (Supplementary Table S6 and Fig. S6), AFM (Supplementary Fig. S7a) and HRTEM (Supplementary Fig. S9) indicate that most of graphene sheets in our products should probably be highly wrinkled and ridged single-layer graphene sheets with likely some few-layer sheets. The results from Raman (Supplementary Fig. S8) and AFM (Supplementary Fig. S7b) both indicate that the single-layer graphene sheets in our products are mainly in the dimensional size of 4–6 nm. And the results from EELS (Supplementary Fig. S4) and the good electrical conductivity suggest primarily sp2-bonded carbon in our products. Thus, a possible 3D structure model of single-layer graphene sheets at the bulk state is proposed and shown in Fig. 3 to rationalize the structural analysis results, where the units are sp2 graphene domains selected with 4–6 nm of dimensional size. This structure was first optimized using molecular mechanics method and then its SSA was calculated to be 3536 m2/g36. These results are consistent with both the experimental and the modeling SSA results above for our products. Note such a model can give agreeable SSA data and support the analysis results presented above such as XRD, EELS, EPR, Raman and etc. Other possible models should also be pursued and studied.

Figure 3
figure 3

The proposed 3D structure model of the porous 3D graphene-based products.

The 3D model of the proposed structure of our porous graphene-based material was established in Materials Studio Modeling (version 4.4, Accelrys), where the units are sp2 graphene domains with dimensional size of 4–6 nm and curved and lapped irregularly. This model was first optimized using molecular mechanics method and its accessible solvent SSA was calculated to be 3536 m2/g using a simple Monte Carlo integration technique where the probe molecule is “rolled” over the framework surface as mentioned above. These results again are consistent with both the experimental and the modeling SSA results above for our products, thus this model could be used as a 3D representative model for our products.

Full size image

Pore size distribution of the ultrahigh SSA

Next, we analyzed the pore size distribution (PSD) of these materials, as it is another key to decide their performance for many applications such as for absorption and supercapacitor materials utilizing their ultrahigh SSA, since if the pore size is too small, the guest molecules or electrolyte ions will not be able to access them43. Based on experimental nitrogen adsorption data, the PSD of our materials were analyzed using a non-local density functional theory (NL-DFT) method with a slit pore model44. As shown in Fig. 4a, our porous 3D graphene-based materials are made of most with pores > 1 nm but < 10 nm and there is significantly less contribution for the micropores with size < 1 nm. This is significantly different from the PSD of the commercial RP20 and other high SSA materials in literatures5,6,45, where the micropores make up most of the total pores (Supplementary Table S7). This larger-size-side shifted PSD indicates these materials should provide better accessibility and more effective SSA (E-SSA) for guest molecules or ions46. Detailed values of E-SSA are shown in Fig. 4b, which were calculated based on the positive ion EMIM+ with size of ~0.76 nm47 when EMIMBF4 was used as electrolyte for supercapacitor48. Thus, our materials not only have ultrahigh overall SSA, but also have much higher E-SSA for guest ion or molecule access compared with the conventional AC and other materials46.

Figure 4
figure 4

PSD and E-SSA of all optimized materials, with G-HA and RP20 for comparison.

(a) PSD of RP20, G-HA and all the optimized materials, which are based on a slit NL-DFT model from the experimental nitrogen adsorption data. (b) E-SSA of these materials when using EMIMBF4 as electrolyte for supercapacitor. Based on these experimental PSD and DFT-SSA data from the NL-DFT method, E-SSA is defined as the part of total DFT-SSA above the size of guest molecules or ions. Positive ion EMIM+ with size of ~0.76 nm which is larger than the negative balancing ion BF4− is considered here. As one example, product PF16G-HA could provide large E-SSA (1710 m2/g), 76% from the total DFT-SSA (2250 m2/g) for the supercapacitor application when EMIMBF4 electrolyte is used. This is contrary to the much lower E-SSA (739 m2/g), 59% of the total DFT SSA (1255 m2/g) for RP20. Our materials not only have ultrahigh overall SSA, but also have much higher E-SSA for guest ion or molecule access compared with the conventional AC and other materials.

Full size image

Discussion

As one example of the applications taking all those advantages of these materials, we studied their applications for supercapacitors, as two of the most important requirements of the current electrode materials used in the state-of-the-art supercapacitors are to have both high E-SSA and good conductivity to achieve both high energy density and power density1,49.

Before we discuss the capacitance performance of our materials, we want to point out that recently, there are strong calls for reporting the supercapacitor performance data following the “clear rules for reporting the performance of new materials”50,51 as many claimed data in recent literatures were not obtained following the reliable measurement method/practice and losing comparison capability and reliability. We want to emphasize that our performance data are based on the practical industry devices (Supplementary Fig. S14) and calculated using the most recommended reliable method (details shown in the Supplementary Information) rather than the three-electrode CV method.

Using these best recommended industry practice and method, we have fabricated and tested supercapacitors using these materials as the electrode materials without any addition of CB due to their both ultrahigh SSA and excellent conductivity. Both the most popular organic electrolyte of 1 M TEABF4/AN and ionic liquid (IL) EMIMBF4 were used as the electrolyte systems. Supercapacitor performance data of these porous 3D graphene-based materials prepared with the optimized ratios of carbon source/GO are listed in Table 2 and Supplementary Table S8. All the products give similar but excellent supercapacitor performance, with the best results coming from the product PF16G-HA which gives a specific capacitance of 202 F/g in 1 M TEABF4/AN and 231 F/g in neat EMIMBF4 electrolyte systems, respectively, at the current density of 1 A/g. The corresponding volumetric capacitance is 80 F/cm3 and 92 F/cm3, based on the volume of electrode films. These are significantly higher than those of commercial RP20 and G-HA and are the best results so far for bulk carbon materials2,8. The detailed galvanostatic charge/discharge curves of the supercapacitors based on these materials in 1 M TEABF4/AN and IL electrolyte systems are shown in Supplementary Figs. S15 and S16. These materials also have superior supercapacitor performance for other electrolyte systems, as shown in Supplementary Table S9 and Fig. S17.

Table 2 Representative supercapacitor performances of porous 3D graphene-based materials. The electrochemical performances were measured using the industry standard two-electrode devices in 1 M TEABF4/AN and neat EMIMBF4 at a constant current density of 1 A/g. The electrode thickness is ~100–120 μm. The performance data of G-HA from pure GO and RP20 under same conditions are listed for comparison. All the experimental values presented are the averaged values and the statistical deviation is about ±5%
Full size table

For the devices based on product PF16G-HA, the corresponding gravimetric energy densities are as high as 51 Wh/kg in 1 M TEABF4/AN and 98 Wh/kg for neat EMIMBF4 electrolyte, based on the active material total weight. For a practical packaged supercapacitor device, the energy density could be estimated to be ~1/3 for the electrode material51, thus this material can exhibit up to ~17 Wh/kg and 33 Wh/kg for a practice industry device in 1 M TEABF4/AN and neat EMIMBF4 electrolytes, respectively. These are much higher than that of the current state-of-the-art commercial supercapacitors52 and comparable with that of lead acid and nickel-metal hydride batteries53, so far the best capacitance performance for all bulk carbon-only materials1,37,54,55.

The devices based on these materials also have excellent rate performance under high current densities in both 1 M TEABF4/AN (Fig. 5a) and neat EMIMBF4 electrolytes (Fig. 5b). For example, even under a high current density of 10 A/g, PF16G-HA based supercapacitors still show a very high specific capacitance of 174 F/g in 1 M TEABF4/AN (Fig. 5c) and 210 F/g in neat EMIMBF4 (Fig. 5d), indicating excellent capacitance retention and rapid ion transport characteristics56. The CV testing of supercapacitors based on our materials in 1 M TEABF4/AN and in neat EMIMBF4 electrolyte exhibit nearly rectangular curves over a wide range of voltage scan rates (50–200 mV/s), also indicating an excellent rate performance (Figs. 5e and 5f, Supplementary Figs. S18 and S19)57.

Figure 5
figure 5

Rate performance of porous 3D graphene-based materials.

Galvanostatic charge/discharge test results of supercapacitors based on the optimized porous 3D graphene-based materials in (a) 1 M TEABF4/AN and (b) neat EMIMBF4 electrolytes under different current densities. Galvanostatic charge/discharge curves of PF16G-HA based supercapacitor under different constant currents in (c) 1 M TEABF4/AN and (d) neat EMIMBF4 electrolyte. Even under a high current density of 10 A/g, PF16G-HA based supercapacitors still show a very high specific capacitance of 174 F/g in 1 M TEABF4/AN and 210 F/g in neat EMIMBF4, indicating excellent capacitance retention and rapid ion transport characteristics; CV curves of PF16G-HA based supercapacitor under different scan rates in (e) 1 M TEABF4/AN and (f) neat EMIMBF4 electrolyte. The CV testing of supercapacitors based on our materials in 1 M TEABF4/AN and in neat EMIMBF4 electrolyte exhibit nearly rectangular curves over a wide range of voltage scan rates (50-200 mV/s), also indicating an excellent rate performance.

Full size image

Further understanding for the high supercapacitor performance of these materials comes from the studies of the powerful electrical impedance spectroscopy (EIS)58. The Nyquist plots for product PF16G-HA in EMIMBF4 systems are shown in Fig. 6a, together with several corresponding samples of PF-HA (from PF only), G-HA and RP-20 for comparison. At high frequency (close to 100 kHz), the corresponding value of the intercept on the X axis represents the intrinsic ohmic resistance of the internal resistance or equivalent series resistance (ESR) of the electrode material and electrolyte59. As shown in Fig. 6a, PF16G-HA based device shows a quite low value (~0.26 Ω) in neat EMIMBF4 electrolyte even with no CB, which is also much lower than the control materials (~0.40 Ω, 1.59 Ω and 1.61 Ω for G-HA, PF-HA and RP20 respectively). Also, the much more inconspicuous loop in the high- to mid-frequency region with a rather lower interfacial charge transfer resistance Rct (~0.5 Ω) for PF16G-HA than the control materials (~0.8 Ω, 0.6 Ω and 1.6 Ω for G-HA, PF-HA and RP20 respectively) indicate a well-connected interface nature of electrolyte ions and electrode56, probably because PF16G-HA has the unique graphene based 3D networks and ultrahigh SSA. Compared with other corresponding samples, product PF16G-HA also demonstrates both the shortest Warburg region portion (inset in Fig. 6a) for an excellent ion diffusion efficiency60 and most vertical curve at the low frequency range for an ideal supercapacitor61. As shown in the expanded view provided in the inset of Fig. 6a, such a closely ideal supercapacitor behavior is even observed at the frequency of ~2 Hz for PF16G-HA based device. This indicates the capacitance could be reached fully at very fast recharging (~0.5 s vs. 2 Hz), which is also consistence with results of frequency response (Fig. 6b)62. Similar EIS and frequency response studies of PF16G-HA obtained in 1 M TEABF4/AN electrolyte are shown in Supplementary Fig. S20, which also demonstrates an ideal supercapacitor behavior with even a smaller internal resistance due to the better conductivity of AN electrolyte system63. Furthermore, all other optimized products such as SU24G-HA, LI24G-HT, CE24G-HA and PVA20G-HA demonstrate a similar and excellent rate and frequency response in both organic and IL systems (Supplementary Figs. S21 and S22, Table S10).

Figure 6
figure 6

EIS for frequency response performance and cycle stability of the supercapacitors.

(a) Nyquist plots of PF16G-HA, PF-HA, G-HA and RP20 with the imaginary part (Y axis) vs the real part (X axis) of impedance from EIS studies measured in the frequency range of 100 kHz to 10 mHz at an AC amplitude of 10 mV in neat EMIMBF4 electrolyte. The inset shows an expanded view for the high frequency range; (b) Frequency response of PF16G-HA, PF-HA, G-HA and RP20 in neat EMIMBF4 electrolyte. (c) Cycle stability of supercapacitors based on PF16G-HA in different electrolytes at a current density of 1 A/g. No obvious decay of capacitance was observed after 5000 constant current charge/discharge cycles in all the electrolytes. For instance, the devices still keep > 99% capacitance in 1 M TEABF4/AN system and 94% in EMIMBF4 system after 5000 cycles.

Full size image

For practical applications, the cycling/life stability of these materials are studied, which show the industry-level supercapacitor devices from these materials all have excellent cycling stability in various electrolyte systems. Fig. 6c shows the cycling performance data for the PF16G-HA. No obvious decay of capacitance was observed after 5000 constant current charge/discharge cycles in all the tested electrolytes at a current density of 1 A/g. For instance, after 5000 times of charging/recharging, the devices still keep > 99% capacitance in 1 M TEABF4/AN system and 94% in EMIMBF4 system. Similarly, other products all show excellent regarding to the life test as shown in Supplementary Fig. S23.

In summary, highly porous 3D graphene-based bulk materials, prepared from various carbon sources including various biomass and cheap polymers with a few percent of GO by a simple and green process, exhibit ultrahigh SSA and good conductivity. The addition of small amount of GO change the product morphology dramatically and offer a truly 3D and porous structure. Various structural and morphology analyses conclude that the materials consist of mainly single-layered curved and defected graphene sheets in the size of a few of nanometers. The ultrahigh SSA is mainly due to the edge carbons. The PSD also shifts to the mesopore side compared to the conventional AC which generally has more micropores. These conclusions should have important implications for the development of sp2 carbon materials with even better properties. The combined superior properties make these materials exhibit excellent performance for supercapacitor in various electrolyte systems without using any conducting filler, which achieve so far the best capacitance and energy density for all bulk sp2 carbon materials in the criteria of the best recommended industry and practical device and evaluation methods. These results, together with the cheap and green and easily-scaled-up method to make these materials, should have significant implications for both academic and industry communities.

Methods

Materials

Graphite (average particle diameter of 44 μm, 99.95% purity, Qingdao Huarun Graphite Co., Ltd.), sucrose, lignin, cellulose (Tianjin Guangfu Chemical Co., Ltd.), PVA (Alfa Aesar), phenol (>99% purity, Tianjin Guangfu Co., Ltd.), formaldehyde aqueous solution (37 wt.%, Tianjin Guangfu Co., Ltd.) and potassium hydroxide (KOH, Wuhan Chujiang Chemical Co., Ltd.) were used as raw materials. 2,2,6,6-Tetramethyl-4-hydroxypiperidin-1-oxyl (TEMPOL, >98% purity, Alfa Aesar), Poly (tetrafluoroethylene) (PTFE, solid powder, Dupont), commercial activated carbon RP20 (Kuraray Chemicals) and electrolytes including 1.0 M tetraethylammonium tetrafluoroborate in AN (TEABF4/AN, Novolyte), 1-Ethyl-3-methylimidazolium tetrafluoroborate (EMIMBF4, Novolyte), 1-Ethyl-3-methylimidazolium bis (trifluoromethylsulfonyl)imide (EMIMTFSI, Novolyte) and 1-Butyl-3-methylimidazolium tetrafluoroborate (BMIMBF4, Novolyte) were all used as purchased. The cellulose film (TF4840, NKK) were used as separator for supercapacitor. Conductive carbon black named Super P (TIMCAL) was used as conducting additives for supercapacitors if necessary. Graphite oxide was prepared using modified Hummers method from flake graphite64,65,66,67.

Preparation of 3D graphene-based materials

The preparation of all the porous 3D graphene-based materials from different carbon sources include a hydrothermal process followed by an industry KOH activation step, as shown in details in Supplementary Information. As a typical example, the preparation of the 3D graphene-based materials from sucrose and GO are described as following. Briefly, according to different weight ratios of sucrose to GO, different volume of sucrose aqueous solution (250 mg/mL) and GO aqueous solution (5 mg/mL) was homogeneously mixed together and transferred to a 100 mL Teflon-lined autoclave and heated to 180°C, then kept for 12 h. After the autoclave was cooled to room temperature, the solid product was washed with distilled water and dried in vacuum at 120°C for 24 h to get the intermediate product. Then, this intermediate product (1 g) was mixed with KOH (4 g) and placed in a horizontal tube furnace, heated to 800°C at 5°C/min and kept for 1 h under Ar. After cooling down to the room temperature, the obtained product was thoroughly washed with 0.1 M HCl and distilled water until the pH value reached 7. The final product was obtained after dried in vacuum at 120°C for 24 h.

Characterization

The morphology of all porous 3D graphene-based materials was analyzed by Scanning Electron Microscopy (SEM) using LEO 1530 VP field emission scanning electron microscope with acceleration voltage of 10 kV. Transmission electron microscopy (TEM) and Electron energy loss spectroscopy (EELS, Gatan) were carried on a JEOL TEM-2100 electron microscope at acceleration voltage of 200 kV. Typical tapping-mode atomic force microscopy (AFM) and scanning tunneling microscope (STM) measurements were taken using Multimode SPM from Digital Instruments with a Nanoscope IIIa Controller. X-ray diffraction (XRD) measurements were performed on a Rigaku D/Max-2500 diffractometer with Cu Kα radiation. Raman spectra were examined with a LabRAM HR Raman spectrometer using laser excitation at 514.5 nm. X-ray photoelectron spectroscopy (XPS) was carried out using AXIS HIS 165 spectrometer (Kratos Analytical) with a monochromatized Al Kα X-ray source (1486.71 eV photons) to analyze the chemical composition of the products. Combustion elemental analysis was also done at Vario Micro cube, (Elementar, Germany) for determination of the C, H, O and N content. Electron paramagnetic resonance (EPR) measurements were done with a Bruker EMX-6/1 with TEMPOL as a standard and the samples were measured in 4 mm tubes under the same number of scans. The nitrogen adsorption/desorption analysis was done at 77 K on a Micromeritics ASAP 2020 apparatus.

Fabrication of working electrode and supercapacitor

Briefly, 90 wt.% products and 10 wt.% PTFE were homogeneously mixed in the agate mortar. Then the mixture was rolled into 100–120 μm thickness sheets and punched into 16 mm diameter electrodes. After dried at 120°C for 6 h under vacuum, the electrodes were weighted and hot pressed onto the current collectors (aluminum foils with conducting carbon coating) and then dried at 180°C for 6 h under high vacuum to completely remove water. The dry electrodes/collectors were transferred into a glove box filled with Ar to construct two-electrode symmetrical supercapacitors, which consisted of two current collectors, two electrodes with identical weight and a porous cellulose separator sandwiched in a test fixture consisting of two stainless steel plates. 30 wt.% KOH aqueous solution, 1.0 M TEABF4/AN, EMIMBF4, EMIMTFSI and BMIMBF4 were used as electrolytes, respectively.

Electrochemical measurements for supercapacitor performances

All the electrochemical tests were carried out at room temperature. Galvanostatic charge-discharge cycle tests were measured using an Arbin testing system (Arbin MSTAT, America). Cyclic voltammetry (CV) and electrical impedance spectroscopy (EIS) studies were performed using Autolab (Metrohm).

Details of the experimental process, including the preparation procedures/conditions, various characterization and measurement, are described in the Supplementary Information.