Abstract
Fabrication and synthesis of plasmonic structures is rapidly moving towards sub-nanometer accuracy in control over shape and inter-particle distance. This holds the promise for developing device components based on novel, non-classical electro-optical effects. Monochromated electron energy-loss spectroscopy (EELS) has in recent years demonstrated its value as a qualitative experimental technique in nano-optics and plasmonic due to its unprecedented spatial resolution. Here, we demonstrate that EELS can also be used quantitatively, to probe surface plasmon kinetics and damping in single nanostructures. Using this approach, we present from a large (>50) series of individual gold nanoparticles the plasmon Quality factors and the plasmon Dephasing times, as a function of energy/frequency. It is shown that the measured general trend applies to regular particle shapes (rods, spheres) as well as irregular shapes (dendritic, branched morphologies). The combination of direct sub-nanometer imaging with EELS-based plasmon damping analysis launches quantitative nanoplasmonics research into the sub-nanometer realm.
Similar content being viewed by others
Introduction
By their very nature, localized surface plasmon resonances are challenging phenomena for near-field experimental scrutiny. On the one hand, the spatial confinement of their electric fields necessitates sub-wavelength precision for the analysis of individual plasmon modes. On the other hand, the Terahertz oscillation frequencies of plasmon resonances in noble metals demand probing with femtosecond accuracy. Despite ongoing instrumental developments1, real-space, femtosecond characterization of plasmon modes in individual particles, or at various locations within single particles with nanometer spatial accuracy has so far not been demonstrated yet.
Here, we propose an approach that overcomes these limitations, accomplishing the quantitative characterization of plasmon kinetics and damping with nanometer spatial precision. Experimental results using this method were obtained with nanoprobe electron spectroscopy having an equivalent temporal resolution down to 2 fs (60 meV spectral resolution achievable at 2 eV). We believe that this experimental capability will find direct applications throughout the plasmonics community2, as the plasmon kinetics can now be measured from user-selected modes in individual structures from which the size, shape and inter-particle distance can be simultaneously resolved with sub-nanometer or even atomic resolution.
Surface plasmon resonances can be described as damped harmonic oscillators3, driven—for example—by the electric component of light. The motion of an underdamped harmonic oscillator is described by4

where the exponential term defines the damping of the oscillations and φ the phase shift. The damping parameter γ and resonance angular frequency ωp determine  and the parameter A is determined by the boundary conditions. The Fourier transform
and the parameter A is determined by the boundary conditions. The Fourier transform  shows that in the frequency domain, the damped harmonic oscillator takes the form of a Cauchy-Lorentz distribution:
shows that in the frequency domain, the damped harmonic oscillator takes the form of a Cauchy-Lorentz distribution:

The parameter γ defines the half-width of the peak amplitude, at half the maximum amplitude. The shape of the peaks in the frequency spectrum therefore directly reveals the damping characteristics: large damping is manifested as a broad Lorentzian peak, while an idealized undamped resonance would appear as a delta function. Exact information on plasmon damping can therefore be obtained if it were possible to accurately extract the peak widths from experimental, frequency-domain spectra. This routine is indeed broadly used for mechanical, electrical and optical systems. However, this practice has not yet been applied accurately to electron beam spectroscopy, mainly due to the non-monochromaticity of electron sources, which introduces unwanted instrumental peak broadening. This work introduces a technique to accurately remove broadening effects in monochromated electron energy-loss spectroscopy (EELS). The measured plasmon peaks can then be quantitatively interpreted, allowing a full-modal, quantitative plasmon analysis of individual nanostructures.
It was anticipated earlier5,6 that EELS would be promising as a nanoscale probing technique for plasmon damping. Only very recently have EELS measurements been reported7 that combine high energy resolution with excellent signal-to-noise ratios, both required for accurate damping analysis. Here, we use these monochromatic EELS acquisition routines in a scanning transmission electron microscope (STEM) and apply them to a series of chemically-synthesized gold nanorods and –crosses that serve as plasmon resonators.
Accurate measurements of surface plasmon damping in nanoparticles require the fulfillment of the following two requirements. Firstly, the experimental energy resolution has to better than the natural widths of the resonant plasmon peaks, which for monocrystalline gold particles can be as narrow as 100 meV. EELS measurements with the required high monochromaticity have only recently become feasible with the introduction of electron monochromators in (S)TEMs8,9. Secondly, the signal-to-noise ratios of the measured spectra have to be high enough to accurately determine the widths of the plasmon peaks. Here we apply a recently introduced experimental acquisition routine called binned gain averaging10, an EELS-based technique that can combine an energy resolution of around 60 meV with signal-to-noise ratios >105, enabling accurate damping analysis of individual plasmon resonances in single nanoparticles. Details of this routine can be found in the Methods section.
The quality factor, or Q-factor, is a widely applied parameter to describe the damping behavior of resonators. Large damping results in a low Q-factor and only a few cycles will be completed before the oscillations die out, while the opposite is true for small damping. The quality factor is defined as the energy E stored in an oscillator, divided by the energy dissipated per radian. As shown in more detail in the Supporting Information, it then follows from equation (1) that the Q-factor can be described as

with Ep representing the plasmon peak energy and Γ the full-width of the plasmon peak at half its maximum amplitude. Equation (3) therefore allows the direct calculation of the quality factor from EELS spectra, as will be shown below. At a fixed plasmon resonance energy, a lower Q-factor will therefore result in a broader plasmon peak; this increased bandwidth indicates the relatively large range of frequencies that can excite highly damped plasmons. A dephasing time T2 can now be defined as 1/γ; this parameter includes the inelastic lifetime (T1, in which photons or electron-hole pairs are formed) and pure dephasing (T2*, the time in which coherence is lost). In other words, all dephasing effects are included in parameter T2, dephasing from changes in both momentum and energy11. Equations (1) and (2) show that in this definition, T2 will represent the period in which the plasmon amplitude has decayed to 1/e times (36.8% of) its maximum value. From equation (3), it then follows that the dephasing time is directly related to the measured full width of the plasmon peaks:

The measurement of this important parameter has motivated several investigations using different frequency or time-resolved optical techniques: time-resolved second12 and third harmonic generation13 autocorrelation measurements, light scattering spectroscopy14, spectral hole burning15, SNOM spectroscopy16, multiphoton photoemission17,18 and interferometric Frequency Resolved Optical Gating19. The use of electron spectroscopy for determining T2, however, is new and complementary to the other techniques because the high spatial resolution of monochromated EELS allows the study of the electron kinetics of single plasmon modes, in individual nanoparticles.
In contrast to optical techniques where metal particles are illuminated by narrow-band laser light, there is considerable instrumental peak broadening in EELS measurements; despite the relatively high monochromaticity, there is an obvious non-zero instrument function. By their nature as damped harmonic oscillators, the plasmon peaks have a Lorentzian resonance profile, but EELS measures the convolution of this Lorentizain line shape with the instrument function. In Wien-type monochromators, as used in this work, the energy spread of the electron beam approximately follows a Gaussian distribution20; the resulting convolution is therefore a Voigt profile. This introduces a challenge in extracting the plasmon line width, since the convolution integral that defines the Voigt profile cannot be evaluated in closed form—it has to be computed numerically. Here, we propose the use of Olivero and Longbothum's accurate empirical approach21 to calculate the Lorentzian plasmon resonance profile from monochromated EELS spectra:

with ΓL, ΓV and ΓG, the widths of the Lorentzian, Voigt and Gaussian profiles, respectively; the constants 0.5346 and 0.2166 in the equation result from empirical fits to the Voigt line width, with an accuracy of 0.02%. Applied to EELS spectra, the Voigt profile ΓV is the measured plasmon peak and the width of the zero-loss peak is approximated by ΓG. Each experimental EELS spectrum contains all plasmon peaks, as well as the full zero-loss peak. It is therefore possible to determine the values of ΓV and ΓG from each spectrum individually, from which ΓL can be calculated. This scheme then allows the quantitative interpretation of the plasmon peak widths in monochromated EELS spectra.
Results
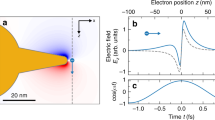
Figure 1 gives an overview of the approach that is used in this work, with experimental results from a single, 210 nm long gold rod. A beam of electrons with a diameter ~1 nm is placed 1–2 nm away from the end of a gold nanoparticle (Fig. 1(a)), exciting damped harmonic plasmon oscillations, Fig. 1(b). Each plasmon resonance mode will then lead to a loss-peak in the frequency-domain EELS spectrum, with a well-defined energy value and width. Fig. 1(c) shows the experimentally obtained EELS spectrum from the gold nanorod and the four main harmonic plasmon modes are indicated. The spectral parameters for each mode were used as input to equation 5, allowing the calculation of the corresponding time-domain spectra of Fig. 1(b). Fig. 1(d) gives an example where the spatial distribution of the various plasmon modes is mapped by applying a recently introduced plot routine22 to our STEM-EELS data.
Surface plasmons in the time- and frequency domains.
(a) A fast electron traverses a gold particle, exciting localized surface plasmons. (b) In the time domain, the various harmonic plasmon modes in this 210 nm long gold nanorod are represented as damped harmonic oscillations. These were calculated from the plasmon energy and peak width measured with EELS (using equation (5)) and were normalized according to their amplitude. (c) The experimental frequency-domain EELS spectrum of the whole particle is plotted here, showing four distinct harmonic plasmon modes. (d) Each plasmon mode has a well-defined spatial distribution of anti-nodes plotted here as a function of distance along the gold rod, corresponding to the aligned TEM image.
Plasmonic effects are often understood in relation to their far-field optical response and it is worth comparing EELS with the more familiar far-field optical methods. The excitation of surface plasmons with fast electrons has been recently reviewed23 and several approaches have been developed to successfully simulate the particle's plasmon response24. Here we use the discrete dipole approximation (DDA) and Green Dyadic Method (GDM) for the efficiency and freedom they offer in defining the volume of the plasmon resonator; details on the used procedures can be found in the Methods section.
Moving beyond single rods, at this point we generalize our approach to include the study of branched and irregularly shaped particles to show that the main plasmon modes of these structures can equally well be analyzed quantitatively with EELS. Figure 2 shows a branched gold nanoparticle, a so-called nanocross25, that was characterized experimentally with EELS and simulated with the DDA and GDM. The figure shows that the resonant plasmon peaks in the EELS spectra are successfully reproduced by the GDM simulations. Experiment and simulations also agree that one or several arms of the gold nanocross can be involved in a single resonance mode. Each arm with its own distinct size and shape has its own spectral response with specific ratios of the main plasmon peaks. The optical response of a suspension of these nanocrosses was also measured and compared to individual EELS spectra from the same suspension. Figure S2 in the Supplementary Information demonstrates that the optical absorption is closely related to the aggregate of all individual bright plasmon modes in the particle suspension.
EELS experiment and DDA/GDM simulations on a gold nanocross.
(a) GDM-simulated spectra (thin dotted lines) and experimental EELS spectra (thick lines), vertically shifted for clarity, including the ‘zero-loss peak’ background signal. The spectra were acquired 1–2 nm off the tip of the four arms at locations I–IV. Bottom: DDA-simulated excitation spectra upon illumination with polarized light, showing the two bright plasmon modes. (b) Top: TEM image of the gold nanocross, with locations I–IV indicated. The schematic at the bottom shows the model that was used for the DDA and GDM simulations. (c) Energy-filtered plasmon maps, showing the spatial distribution of EELS losses in 0.2 eV wide energy windows at the three main plasmon resonances for this nanocross, at 1.1, 1.6 and 1.9 eV. The experimental results (top) have the same colour table as the simulations (bottom), mapping the local EELS amplitude.
More detail from an individual particle is given by the DDA simulation where the same geometry from Fig. 2 is illuminated by linearly- or circularly polarized light, confirming the retardation-induced energy shift in the plasmon modes between far-field and near-field26,27. Another important difference between far-field optics and near-field techniques such as EELS, is that more resonant plasmon modes can be excited by the latter. This includes the bright plasmon modes that are also observed with far-field techniques, as well as the so-called dark modes28 that due to their non-uniform field vector are only accessible with near-field techniques. The experimental and simulated EELS spectra and maps in Figure 2 show a resonant plasmon mode around 1.9 eV, while the far-field optical DDA simulations do not show this dark mode. The accessibility of dark modes with EELS makes it a powerful technique for full-modal characterization of surface plasmons.
Figure 3 presents results from EELS measurements performed on >50 individual gold particles with different aspect ratios, diameters and geometries, i.e. nanorods and -crosses. The overall trends agree with earlier simulations29,30,31 and optical experiments14. In the near-infrared energy range below 1.6 eV where the aspect ratios of the particles are large, radiation damping is dominant. For very low energies, the electrons oscillate more out of phase with photons and these retardation effects reduce Q relatively gently26. Above a material-specific threshold energy, plasmons can decay into ‘hot’ electron-hole pairs. For gold, the energy difference between the 5d-band and the conduction band is around 1.8 eV, resulting in the abrupt decrease of Q and T2 above this resonance energy14,32,33. It has been shown that these electron-hole pairs could even be harvested by an adjacent semiconductor, resulting in a plasmon-assisted photocurrent34.
Quality factors and Dephasing times for gold particles with varying diameters.
(a) The Q-factor and (b) T2, as a function of plasmon energy for gold nanorods (blue filled symbols) and nanocrosses (red open symbols); error bars indicate the standard deviation. The STEM annular dark field images in the legend show a few examples of studied particles, all scaled to be mutually comparable in size. Simulations are for 25, 30 and 35 nm wide gold rods (grey dotted lines), calculated from earlier published Boundary Element Method results24.
Figure 3 also includes information on the geometry of the particles. The particle diameters from the measured gold nanorods (blue filled symbols) and gold nanocrosses (red open symbols) ranged from 18 to 40 nm. The legend of Fig. 3 shows STEM images with some examples from the more than 50 particles that were included in the analysis. The diameter of the particles was determined by taking the average diameter of the whole rod, or of the arm of the nanocross where the spectrum was measured. Nanocrosses are a novel family of dendritic gold nanostructures25,35,36 that can have arms of different lengths and orientation. The nanorods studied here were monocrystalline, but the nanocrosses had up to five large crystal grains, resulting from fivefold twinning. EELS measurements were always performed by placing the STEM probe 1–2 nm off the tip of an arm, while acquiring a spectrum (as indicated by the symbols I-IV in Fig. 2 for example). Numerical simulations based on the Boundary Element Method37 published by Myroshnychenko et al.24 are indicated by the grey dotted lines, showing Q and T2 for gold rods with diameters of 25, 30 and 35 nm. Despite that fact that no data are available below 1.4 eV for these simulations in the literature, they do indicate that the highest Q and T2 values are expected for the thinnest particles in our series, as confirmed by the experiments.
Once the resonance energy is established by the shape of the particle—a rod, a cross or otherwise—a general, frequency-dependent trend is obtained for the plasmon damping parameters, shown by the overlap between the data from the rods and from the crosses in Fig. 3. It should be noted that proximity- and confinement effects could cause divergences from the trend, but these effects are not affecting the current results as we studied relatively large particles, well-separated in space from one another and with relatively large gaps between the nanocross arms. Other reasons that could cause a shift in the damping plots are for example the introduction of polycrystallinity, a change in the dielectric constant of the material or environment, or variations in the particle radii26. An example of this is indicated in Fig. 3 by the vertical shift due to the variation in the particle diameter.
The accuracy of the measurements needs some discussion. The variance in the widths of the plasmon peaks was determined case-by-case; a spectrum with a single well-resolved plasmon peak allowed more accurate determination of Γ than a spectrum with two overlapping peaks. The standard deviation that is indicated by the error bars was estimated by repeated fitting of Lorentzians to the plasmon peaks and minimizing the residual. Due to the high monochromaticity of the experiments, the Voigt lineshape of the plasmon peaks was very close to that of a Lorentzian, examples of which will be shown in Fig. 4, confirming the nature of plasmons as damped harmonic oscillators.
Quantitative mapping of the Quality factors and Dephasing times of individual plasmon modes in a single gold particle.
(a) Experimental EELS spectra from locations I–IV, showing three dominant plasmon modes in an irregularly-shaped gold cross. Before subtracting the background, the zero-loss peak (ZLP) maxima of the spectra were normalized. (b) The EELS spectrum from location III, showing an example of the fitting of three Lorentzians. The sum of the three Lorentzians and the EELS data are shifted vertically for clarity and their peak widths are shown. (c) Overlaid, colour-coded EELS maps from the three dominant plasmon modes, with in the legend their Q and T2 values. On the EELS maps, the STEM annular dark field image of the nanocross is projected in grayscale40. Locations I–IV are indicated on the map, 1–2 nm off the tip of the arms.
The results presented in Fig. 3 were from EELS measurements each obtained in only one location, i.e. 1–2 nm off the particle. However, it is also possible to raster-scan the electron probe in the whole area around the particle, which allows the spatial mapping of surface plasmon modes6,22,38,39, and—as will be demonstrated here—of the damping parameters.
Figure 4 shows an example from a gold nanocross that carries three main plasmon modes. Using the experimental and data processing routines described in the Methods section, EELS plasmon maps are extracted, colour-coded and assigned the Q and T2 values that result from the spectral analysis shown in Fig. 4(a) and (b), followed by the application of equations 3–5. The variances for Q and T2 were calculated from the sample standard deviation propagating from the Lorentzian fitting to the four spectra from locations I–IV. The combination of the EELS maps and the STEM dark-field image directly relates the local plasmon modes to the particle geometry.
Discussion
The presented approach to quantitatively analyze and map Q and T2 are generally applicable to plasmon-active structures and nanoparticles of any shape, size and material. The accuracy depends firstly on the spectral overlap of the various plasmon modes, which are determined by the local geometry and secondly on the quality of the spectra, which is determined by the used hardware, alignments and acquisition routines. Current state-of-the-art experimental methods make it possible to obtain high spectral accuracy throughout the ultraviolet and visible. The background signal increases at low energies, resulting in relatively high variances for Q and T2 into the mid-infrared, hampering accurate quantification at energies below 0.4 eV, while STEM-EELS analysis in the far-infrared below 0.1 eV is currently out of experimental reach. The calculation of Q and T2 does not require information about the geometry of the particles, which further broadens the scope of this technique. Their values can also be extracted from short or irregularly-shaped structures, as is the case for example for the red-coded plasmon around location IV in Fig. 4(c), for which the diameter cannot be measured with any accuracy.
In summary, an approach was presented for measuring the quality factor and the dephasing time of surface plasmon resonances, using monochromated STEM-EELS. This technique makes it possible to quantitatively map the values of Q and T2 of individual plasmon modes in single nanostructures with (sub-)nanometer spatial accuracy. Using this approach, a large series of gold nanorods and -crosses was measured and it was shown that the damping parameters follow a general trend, largely independent of the particle shape. The broad spectral range that is covered includes the near-infrared, visible and ultraviolet, giving access to a much broader range of frequencies than is possible with all-optical experiments. The very high spatial resolution, broad spectral sensitivity and general applicability of the presented approach makes it uniquely positioned for the study of electron kinetics and plasmon damping at nanometer length scales. Applications of the presented method are broad and include assessing the effect of polycrystallinity on plasmon damping, sub-nanometer probing of plasmon-assisted electron tunnelling41 and due to the ease with which an electron beam excites plasmons, it can serve as a common platform to mutually compare the performance of novel plasmonic materials and devices.
Methods
Synthesis of gold nanocrosses
In a typical synthesis of gold nanocrosses, 2.0-mmol copper(I) chloride (CuCl, 99%) was first dissolved in 5-ml oleylamine (70%) and heated at 200°C for 10 minutes. After cooling to 50°C, a solution of 0.3 mmol gold(III) chloride (AuCl3, ≥99.99%) in 5-ml oleylamine was injected and maintained at this temperature for one hour. After centrifugation, the supernatant was heated to 100°C and reacted for 30 minutes. The obtained gold nanocrosses were purified three times by precipitation/re-dispersion using the solvent mixture of ethanol (99%)/hexane (85%) and dispersed in hexane for further use. Optical absorption spectra (see for example figure S1 in the Supplement) were done with a Shimadzu UV-Vis-NIR spectrometer (UV3150), after dispersing the gold nanocrosses in tetrachloroethylene.
Synthesis of gold nanorods
We followed the three-step seed-mediated method that introduced by Jana et al.42 In brief, 20 ml gold seeds aqueous solution containing HAuCl4·3H2O (≥99.9%, 2.5·10−4 M) and tri-sodium citrate dihydrate (≥99.9%, 2.5·10−4 M) was prepared in a 22 ml glass vial. Then, 0.6 ml of an aqueous ice-cold NaBH4 (CTAB, ≥99.9%, 0.1 M) was added at once into the growth solution. The solution was allowed to stir for 2 hours before proceeding to the next step. A 30 ml growth solution containing CTAB (0.1 M) and HAuCl4·3H2O (2.5·10−4 M) was prepared. This growth solution was distributed into three polypropylene tubes (labeled A, B and C) with 9 ml each. Next, 0.05 ml of L-ascorbic acid (Biotra, ≥99.9%, 0.1 M) was added into each tube followed by gentle inversion mixing. Then, 1.0 ml of the gold seeds solution was added into tube A. After 15 s, 1.0 ml from tube A was transferred into tube B. After another 15 s, 1.0 ml from tube B was transferred from tube B into tube C. The solution in tube C which contained gold nanorods, spheres and plates, was subjected to centrifugation for shape separation. Typically, 1.5 ml of the particle solution was centrifuged at 2000 rpm for 6 minutes for several times. The supernatant was poured off and the solid part containing nanorods and plates was re-dispersed in about 0.1 ml of ultra-pure deionized water.
DDA simulations
The far-field extinction spectra of the model nanocross have been simulated using the discrete dipole approximation (DDA) implemented in DDSCAT software43,44. The optical index and extinction coefficient of gold were taken from Johnson and Christy45. The gold nanocross was modeled using nearly sixty thousand dipoles that reproduce the actual shape, size and arrangement of the nanocross branches shown in Figure 2. The excitation of surface plasmons by the monochromatic electron beam has been simulated using the Green dyadic method (GDM)46,47,48, which is particularly adapted to the analysis of the EELS signal generated by fast electrons impinging a metal particle46. The Green dyadic tensor  is computed by meshing the model nanocross with 8850 cubic cells and solving numerically Dyson's equation46,47. The EELS signal is proportional to the local density of states (LDOS) which, for a given loss energy E reads
is computed by meshing the model nanocross with 8850 cubic cells and solving numerically Dyson's equation46,47. The EELS signal is proportional to the local density of states (LDOS) which, for a given loss energy E reads  , where the imaginary part and the trace of the tensor S are used. The LDOS spectra were computed at the sites I-IV, located in the plane of the nanocross as shown in Fig. 2.
, where the imaginary part and the trace of the tensor S are used. The LDOS spectra were computed at the sites I-IV, located in the plane of the nanocross as shown in Fig. 2.
Nanobeam spectroscopy
Gold particles were dispersed on a ~10 nm thick SiO2 support film (TEMwindows) and cleaned for 40 s in an Argon(75%)-Oxygen(25%) plasma, to remove organic surfactants. EELS was performed in STEM mode using an FEI Titan TEM with Schottky electron source, operated at 80 kV, using a convergence semiangle of 13 mrad. A Wien-type monochromator dispersed the electron beam in energy and a narrow energy-selecting slit formed a monochrome electron beam with typical full-width at half-maximum values of 50–70 meV and full width at 1/1000 of maximum values around 0.7 eV. The electron beam was focused to a probe with a diameter less than 1 nm. Attached to the TEM was a Gatan Tridiem ER EELS detector used for EELS mapping and spectroscopy, applying a 7 mrad collection semiangle. EELS was acquired with a modified binned gain averaging routine10: individual spectra were acquired in 40 ms, using 16 times on-chip binning. The detector channel-to-channel gain variation was averaged out by constantly changing the readout location and correcting for these shifts after completing the EELS acquisition. Subtraction of the quasi-elastic EELS background signal was performed by fitting a pre-measured zero-loss peak spectrum to the data. Examples of this background profile can be seen in Fig. 2(a), at the low-energy side of the experimental spectra it shows as a decreasing slope. This profile was obtained from a sample area far from the presence of particles, fitted to the data and subtracted. A high-quality dark reference was acquired separately and used for post-acquisition dark signal correction. Spectra were normalized by giving the maximum of the spectra (the top of the zero-loss peak) unit value. All spectra were acquired 1–2 nm off the metal surfaces. Typical signal-to-noise ratios of 105 for individual spectra were obtained.
EELS mapping
Two methods were used to obtain EELS maps: (1) Energy-filtered mapping and (2) Spectrum Imaging. Energy-filtered mapping was done by applying the same narrow energy-selecting slit as used for spectroscopy, but now the electron beam is set to converge only a few mrad, much less than in STEM mode. The EELS detector then imaged the particle using electrons in 0.2 eV energy windows around selected plasmon peaks. The relatively high non-isochromaticity of the EELS detector required the use of only the central ~30% of the detector CCD, where the non-isochromaticity was measured to be smaller than 0.1 eV. In this way, energy-filtered plasmon maps were obtained at the main plasmon energies.
Spectrum imaging was done by scanning a small electron probe with an approximate diameter of 1 nm in a rectangular raster of pixels, while at each pixel an EELS spectrum is collected and stored. After data processing as described above, 0.1 eV energy windows around the plasmon peaks of interest were used to image the EELS intensity in each pixel in linear scale. The EELS intensity maps were colour-coded and overlaid with the STEM annular dark field image of the same particle.
References
Zewail, A. H. 4D ultrafast electron diffraction, crystallography and microscopy. Annu. Rev. Phys. Chem. 57, 65–103 (2006).
Stockman, M. I. Nanoplasmonics: past, present and glimpse into future. Opt. Express 19, 22029–22106 (2011).
Zuloaga, J. & Nordlander, P. On the energy shift between near-field and far-field peak intensities in localized plasmon systems. Nano Lett 11, 1280–1283 (2011).
Feynman, R. P., Leighton, R. B. & Sands, M. The Feynman Lectures on Physics. Vol. 1, Chapter 24, Addison-Wesley, Reading MA, (1963).
Batson, P. E. Damping of bulk plasmons in small aluminum spheres. Solid State Comm. 34, 477–480 (1980).
Bosman, M., Keast, V. J., Watanabe, M., Maaroof, A. I. & Cortie, M. B. Mapping surface plasmons at the nanometre scale with an electron beam. Nanotechnology 18, 165505 (2007).
Duan, H., Fernández-Domínguez, A. I., Bosman, M., Maier, S. A. & Yang, J. K. W. Nanoplasmonics: classical down to the nanometer scale. Nano Lett. 12, 1683–1689 (2012).
Mook, H. W. & Kruit, P. Construction and characterization of the fringe field monochromator for a field emission gun. Ultramicroscopy 81, 129–139 (2000).
Koch, C. T., Sigle, W., Höschen, R., Rühle, M., Essers, E., Benner, G. & Matijevic, M. SESAM: exploring the frontiers of electron microscopy. Microscopy and Microanalysis 12, 506–514 (2006).
Bosman, M. & Keast, V. J. Optimizing EELS acquisition. Ultramicroscopy 108, 837–846 (2008).
Luk'yanchuk, B. S., Tribelsky, M. I., Ternovsky, V., Wang, Z. B., Hong, M. H., Shi, L. P. & Chong, T. C. Peculiarities of light scattering by nanoparticles and nanowires near plasmon resonance frequencies in weakly dissipating materials. J. Opt. A: Pure Appl. Opt. 9, S294–S300 (2007).
Lamprecht, B., Leitner, A. & Aussenegg, F. SHG studies of plasmon dephasing in nanoparticles. Appl. Phys. B: Lasers and Optics 68, 419–423 (1999).
Lamprecht, B., Krenn, J. R., Leitner, A. & Aussenegg, F. R. Resonant and off-resonant light-driven plasmons in metal nanoparticles studied by femtosecond-resolution third-harmonic generation. Phys. Rev. Lett. 83, 4421–4424 (1999).
Sönnichsen, C., Franzl, T., Wilk, T., von Plessen, G. & Feldmann, J. Drastic reduction of plasmon damping in gold nanorods. Phys. Rev. Let. 88, 077402 (2002).
Bosbach, J., Hendrich, C., Stietz, F., Vartanyan, T. & Träger, F. Ultrafast dephasing of surface plasmon excitation in silver nanoparticles: influence of particle size, shape and chemical surrounding. Phys. Rev. Lett. 89, 257404 (2002).
Klar, T., Perner, M., Grosse, S., von Plessen, G., Spirkl, W. & Feldmann, J. surface-plasmon resonances in single metallic nanoparticles. Phys. Rev. Lett. 80, 4249 (1989).
Lehmann, J., Merschdorf, M., Pfeiffer, W., Thon, A., Voll, S. & Gerber, G. Surface plasmon dynamics in silver nanoparticles studied by femtosecond time-resolved photoemission. Phys. Rev. Lett. 85, 2921–2924 (2000).
Scharte, M., Porath, R., Ohms, T., Aeschlimann, M., Krenn, J., Ditlbacher, H., Aussenegg, F. & Liebsch, A. Do Mie plasmons have a longer lifetime on resonance than off resonance? Appl. Phys. B: Lasers and Optics 73, 305–310 (2001).
Anderson, A., Deryckx, K. S., Xu, X. G., Steinmeyer, G. & Raschke, M. B. Few-femtosecond plasmon dephasing of a single metallic nanostructure from optical response function reconstruction by interferometric frequency resolved optical gating. Nano Lett. 10, 2519–2524 (2010).
Tiemeijer, P. C., Bischoff, M., Freitag, B. & Kisielowski, C. Using a monochromator to improve the resolution in TEM to below 0.5 Å. Part I: Creating highly coherent monochromatd illumination. Ultramicroscopy 114, 72–81 (2012).
Olivero, J. J. & Longbothum, R. L. Empirical fits to the Voigt line width: a brief review. J. Quant. Spectrosc. Radiat. Transfer 17, 233–236 (1977).
Rossouw, D., Couillard, M., Vickery, J., Kumacheva, E. & Botton, G. A. Multipolar plasmonic resonances in silver nanowire antennas imaged with a subnanometer electron probe. Nano Lett. 11, 1499–1504 (2011).
García de Abajo, F. J. Optical excitations in electron microscopy. Rev. Mod. Phys. 82, 209–275 (2010).
Myroshnychenko, V., Rodríguez-Fernández, J., Pastoriza-Santos, I., Funston, A. M., Novo, C., Mulvaney, P., Liz-Marzán, L. M. & García de Abajo, F. J. Modelling the optical response of gold nanoparticles. Chem. Soc. Rev. 37, 1792–1805 (2008).
Ye, E., Win, K. Y., Tan, H. R., Lin, M., Teng, C. P., Mlayah, A. & Han, M.-Y. Plasmonic gold nanocrosses with multidirectional excitation and strong photothermal effect. J. Am. Chem. Soc. 133, 8506–8509 (2011).
Bryant, G. W., García de Abajo, F. J. & Aizpurua, J. Mapping the plasmon resonances of metallic nanoantennas. Nano Lett. 8, 631–636 (2008).
Zuloaga, J. & Nordlander, P. On the energy shift between near-field and far-field peak intensities in localized plasmon systems. Nano Lett. 11, 1280–1283 (2011).
Stockman, M. I., Faleev, S. V. & Bergman, D. J. Localization versus delocalization of surface plasmons in nanosystems: can one state have both characteristics? Phys. Rev. Lett. 87, 167401 (2001).
Della Valle, G., Søndergaard, T. & Bozhevolnyi, S. I. High-Q plasmonic resonators based on metal split nanocylinders. Phys. Rev. B 80, 235405 (2009).
Khurgin, J. B. & Sun, G. Scaling of losses with size and wavelength in nanoplasmonics and metamaterials. Appl. Phys. Lett. 99, 211106 (2011).
Biagioni, P., Huang, J.-S. & Hecht, B. Nanoantennas for visible and infrared radiation. Rep. Prog. Phys. 75, 024402 (2012).
Hu, M., Novo, C., Funston, A., Wang, H., Staleva, H., Zou, S., Mulvaney, P., Xia, Y. & Hartland, G. V. Dark-field microscopy studies of single metal nanoparticles: understanding the factors that influence the linewidth of the localized surface plasmon resonance. J. Mater. Sci. 18, 1949–1960 (2008).
Zorić, I., Zäch, M., Kasemo, B. & Langhammer, C. Gold, platinum and aluminum nanodisk plasmons: material independence, subradiance and damping mechanisms. ACS Nano 5, 2535–2546 (2011).
Knight, M. W., Sobhani, H., Nordlander, P. & Halas, N. J. Photodetection with active optical antennas. Science 332, 702–704 (2011).
Mazzucco, S., Stéphan, O., Colliex, C., Pastoriza-Santos, I., Liz-Marzan, L. M., Garcia de Abajo, F. J. & Kociak, M. Spatially resolved measurements of plasmonic eigenstates in complex-shaped, asymmetric nanoparticles: gold nanostars. Eur. Phys. J. Appl. Phys. 54, 33512 (2011).
Mayoral, A., Magen, C. & Jose-yacaman, M. Nanoscale mapping of plasmon resonances of functional multibranched gold nanoparticles. Chem. Commum. 48, 8667–8669 (2012).
García de Abajo, F. J. & Howie, A. Retarded field calculation of electron energy loss in inhomogeneous dielectrics. Phys. Rev. B 65, 115418 (2002).
Nelayah, J., Kociak, M., Stéphan, O., García de Abajo, F. J., Tencé, M., Henrard, L., Taverna, D., Pastoriza-Santos, I., Liz-Marzán, L. M. & Colliex, C. Mapping surface plasmons on a single metallic nanoparticle. Nat. Phys. 3, 348–353 (2007).
Schaffer, B., Grogger, W., Kothleitner, G. & Hofer, F. Comparison of EFTEM and STEM EELS plasmon imaging of gold nanoparticles in a monochromated TEM. Ultramicroscopy 110, 1087–1093 (2010).
Bosman, M., Anstis, G. R., Keast, V. J., Clarke, J. D. & Cortie, M. B. Light splitting in nanoporous gold and silver. ACS Nano 6, 319–326 (2012).
Wu, L., Duan, H., Bai, P., Bosman, M., Yang, J. K. W. & Li, E. P. Fowler-Nordheim tunneling induced charge transfer plasmons between nearly-touching nanoparticles. ACS Nano 7, 707–716 (2013).
Jana, N. R., Gearheart, L. & Murphy, C. J. Wet chemical synthesis of high aspect ratio cylindrical gold nanorods. J. Phys. Chem. B 105, 4065–4067 (2001).
Draine, B. T. & Flatau, P. J. User guide to the discrete dipole approximation code DDSCAT 7.0, arXiv:0809.0337v5. (2008).
Draine, B. T. & Flatau, P. J. Discrete-dipole approximation for periodic targets: theory and tests. J. Opt. Soc. Am. A. 25, 2593 (2008).
Johnson, P. B. & Christy, R. W. Optical constants of the noble metals. Phys. Rev. B. 6, 4370–4379 (1972).
Colas des Francs, G., Girard, C., Weeber, J.-C., Chicanne, C., David, T., Dereux, A. & Peyrade, D. Optical analogy to electronic quantum corrals. Phys. Rev. Lett. 86, 4950 (2001).
García de Abajo, F. J. & Kociak, M. Probing the photonic local density of states with electron energy loss spectroscopy. Phys. Rev. Lett. 100, 106804–4 (2008).
Girard, C. Near–field in nanostructures. Rep. Prog. Phys. 63, 1883–1933 (2005).
Acknowledgements
The authors acknowledge Paul Thomas (Gatan, UK), Timothy Petersen (Monash University, Melbourne, Australia) and Markus Heidelmann (F.Z. Jülich and RWTH Aachen, Germany) for EELS data processing scripts. This work was supported by the computing facility center CALMIP at Paul Sabatier Toulouse University. The National Research Foundation (NRF) is kindly acknowledged for supporting this research under the CRP program (award No. NRF-CRP 8-2011-07 to C.A.N, M.B. and J.K.W.Y.)
Author information
Authors and Affiliations
Contributions
E.Y synthesized the gold nanocrosses and performed optical spectroscopy; S.F.T. and C.A.N synthesized the gold rods. M.B., J.K.W.Y and M.-Y.H. developed the analysis routines, while A.M., A.A. and R.M., C.G. performed DDA and Green dyadic simulations. M.B designed and performed the EELS experiments, processed the data and wrote the manuscript, with input from all authors.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information Surface Plasmon Damping Quantified with an Electron Nanoprobe
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Bosman, M., Ye, E., Tan, S. et al. Surface Plasmon Damping Quantified with an Electron Nanoprobe. Sci Rep 3, 1312 (2013). https://doi.org/10.1038/srep01312
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01312
This article is cited by
-
Alignment-invariant signal reality reconstruction in hyperspectral imaging using a deep convolutional neural network architecture
Scientific Reports (2022)
-
Plasmonic Applications of Gold-Copper Bimetallic Alloy Nanoparticles
Plasmonics (2022)
-
Spontaneous and stimulated electron–photon interactions in nanoscale plasmonic near fields
Light: Science & Applications (2021)
-
Near field excited state imaging via stimulated electron energy gain spectroscopy of localized surface plasmon resonances in plasmonic nanorod antennas
Scientific Reports (2020)
-
Controlling free electrons with optical whispering-gallery modes
Nature (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.