Introduction

A common trait of most sensory neurons in vertebrates is their capacity to adapt to changes of the input signal being monitored. Adaptation in this context is intended as the ability of the sensory cell to shift the window of amplitudes in which the signal is accurately detected without incurring in saturation-induced distortions. Physiological recordings have identified the phenomenon in olfactory receptors1, retinal photoreceptors2, auditory3 and somatosensory neurons4. In this paper we will focus on the first two such sensory systems, olfactory transduction and phototransduction. If it is commonly accepted that the mechanisms inducing adaptation in sensory receptor cells are those involved in the homeostatic regulation of the signaling pathways5,2, there is still no commonly accepted explanation of how this function is performed. In spite of a wealth of knowledge available at the level of molecular components and of reaction mechanisms for the signaling cascades involved and for their regulation (see e.g. Refs. 6,7,8,9 for comprehensive surveys of olfactory transduction and phototransduction), what is still missing (and difficult to obtain) is a complete understanding of how the various steps are orchestrated into a coherent behavior at system-level. Our aim in this paper is to combine mathematical modeling and single cell electrophysiological experiments, in particular input-output (i.e., stimulus-response) time series, to thoroughly understand a number of dynamical features which can be associated with sensory adaptation, thereby helping understanding how this phenomenon happens.

The ability of a biological system to adjust the sensitivity in a wide range of input amplitudes, has been extensively studied in the literature10,11,12,13, especially in recent years14,15,16,17,18,19,20,21,22,23,24. The phenomenon occurs in different contexts, like chemotaxis in bacteria14,24 and amoeba19, osmotic regulation in yeast25, tryptophan regulation in E.coli26 and sensory systems17,12,13. Most, if not all, of these studies evaluate adaptation through the steady state values reached in response to different constant stimuli. When one is concerned only with steady states and their variations, then the only form of adaptation which can be studied is what we call step adaptation. This dynamical behavior is also known as desensitization in the literature12 and corresponds to a response that terminates or attenuates in spite of a persistent stimulation. Following the literature, step adaptation is called perfect (“absolute” Koshland et al.11) in the first case and partial in the second, see Figure 1B for a sketch of the two cases. From a modeling perspective, the perfect adaptation case is of particular interest, because it entails the presence of a particular form of regulation known in control theory as integral feedback24. Perfect step adaptation means that, regardless of the amplitude of the input step being applied, the system is able to recover exactly the nominal value it had before the stimulus.

Figure 1
figure 1

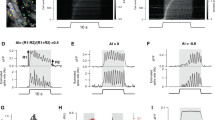
Step and multipulse adaptation.

(A) The basic model (1) consists of the two variables y and x linked by a negative feedback loop (of gains k1 and k2), an external input u and two first order degradation terms (of rates δx and δy). (B) Various levels of adaptation for the model (1), according to the ratio δx/δy. The upper and lower parts of the panel show the response to the two main input protocols described in the text, steps and multiple pulse pairs (here a series of 4 pulse pairs in which the second pulse is progressively delayed with respect the first; the 4 double pulse responses are shown all simultaneously and the 4 first pulses of each pair are all identical and overlapping). Notice that the step responses resembles those of Figure 5 of Koshland et al.11. The ratio δx/δy determines the amount of the two forms of adaptation mentioned in the text, step adaptation and multipulse adaptation. In particular perfect step adaptation requires exact integral feedback (i.e., δx = 0) and corresponds to no recovery in multipulse adaptation (leftmost plots). Moving from left to right of the panel as we increase the ratio δx/δy, step adaptation decreases and the recovery in multipulse adaptation becomes faster. See Supplementary Figure S1 for blown-up plots of the various cases.

Full size image

If, as in our sensory systems, we are able to apply a richer class of input profiles than just steps, then more features than simply steady state responses can be studied. From a dynamical perspective, in fact, the stimulation with time-varying input protocols provides information which is nonredundant with the steady state responses. Combining this with the possibility of monitoring precisely the entire time history of a response, then more fine-graded hypotheses on the regulatory mechanisms encoded in the pathways can be formulated theoretically and validated (or falsified) experimentally. For instance, if in a system with integral feedback instead of steps we apply a pair of nonoverlapping pulses, no difference should emerge in the elicited responses as we progressively increase the delay of the second pulse with respect to the first. This is not what happens in sensory systems: if for short delays between the pulses adaptation manifests itself in a reduced amplitude of the transient response to the second pulse, increasing the lag time adaptation progressively reduces, until the system recovers completely, i.e., the two pulses elicit identical responses. This effect, which we call multipulse adaptation, translates into an integral feedback which cannot be perfect, but which has to “forget” the past with a certain time constant. Exact integral feedback (which corresponds to an infinite time constant) cannot achieve this, but a dynamical feedback with a suitable memory decay can accomplish the task. However, replacing an exact integral feedback with a dynamical feedback having a memory decay implies that perfect step adaptation is no longer possible. Also this prediction is coherent with the experiments. In both sensory systems, in fact, the step responses reset themselves only partially, never completely. While the gap is minimal in the olfactory neurons, it is consistent in phototransduction, see Figure 2A and Figure 3A.

Figure 2
figure 2

Olfactory transduction.

(A) In red, an example of a normalized response to a stimulus of IBMX sustained for 24 s, applied to a salamader olfactory sensory neuron. In blue the fit with the dynamical model (S9) described in the Supplementary Information. (B) Examples of normalized responses to two identical pulses of IBMX of duration 20 ms, applied with a time interval Δt of 6, 10 and 15 s respectively (red traces). In blue the corresponding fits with the dynamical model (S9). Experiments were performed on two isolated olfatory neurons from Ambystoma Tigrinum salamander (one for panel A and one for panel B).

Full size image
Figure 3
figure 3

Phototransduction.

(A) The red traces show an example of normalized response to a step sustained for 20 s in non saturating light conditions. The blue traces show the response of the dynamical model (S11) described in the Supplementary Information. (B) Example of normalized response from two identical non saturating light pulses with a duration of 5 ms applied with a time interval Δt of 2, 3, 4 and 5 s respectively (red traces). In blue the fit of the dynamical model (S11) is shown. Experiments were performed with light at wavelength 491 nm and with suction-electrode recording method from two isolated and intact Xenopus laevis rods (one for panel A and one for panel B) in dark-adapted conditions.

Full size image

In Ref. 17 we have observed that the two forms of adaptation mentioned so far, step adaptation and multipulse adaptation, appear to be in a dynamical trade-off: the more step adaptation gets closer to perfect, the slower is the recovery in multipulse adaptation and viceversa. The limiting case of perfect step adaptation corresponds to no recovery at all in multipulse adaptation. In the present paper this trade-off is investigated more in detail from both a theoretical and an experimental perspective. In particular, we observe that both our sensory systems obey to the rules imposed by this trade-off and the fact can be neatly observed in the transient profiles of the electrophysiological recordings. We show that the trade-off is naturally present also in basic regulatory circuits and that the time constant of the dynamical feedback can be used to decide the relative amount of the two forms of adaptation. These elementary circuits help us understanding the key ingredients needed to have both forms of adaptation and confuting potential alternative models. For example, while it is in principle possible to realize some form of recovery in multipulse adaptation also in presence of exact integral feedback, we show that this requires necessarily a transient response that undershoots its baseline level during the deactivation phase, something that is not observed experimentally in neither sensor. However, if we manage to artificially shift the baseline level (for example performing phototransduction experiments in dim background light rather than in dark) then our simplified model predicts that nonnegligible undershoots in the deactivation phase should emerge. We have indeed verified their presence in experiments.

Results

Stimulus-response behavior for various input protocols

Several input protocols, i.e., classes of time courses given to the stimulus are used in the paper for our two sensory systems:

  1. 1

    steps;

  2. 2

    repeated pulses at different lag times;

  3. 3

    double (nested) steps.

We have applied the first two protocols to olfactory neurons and photoreceptors, obtaining electrical recordings like those shown in Figures 2–3. The double step is instead used only for phototransduction (shown in Figure 4).

Figure 4
figure 4

Double step responses.

(A) Double step protocol applied to the model (1). While the step response never exhibits deactivation undershooting (i.e., upon termination of the step the output returns to its baseline without crossing it over), in a stimulation with a double step, the deactivation of the inner step shows a drop in the output that undershoots the shifted baseline. (B) Example of normalized response (red traces) to a double step of non saturating light for Xenopus laevis rod (a different rod cell than Figure 3 has been used); the two nested steps have a duration of 60 and 20 s. The deactivation transients of the inner step overshoots the steady state corresponding to the outer step. The fitting for the model (S11) is shown in blue.

Full size image

The responses to these input protocols for the two systems exhibit several common features which are highlighted below:

  1. 1

    step response: we observe a transient excursion followed by a decline of the output signal, which tends to return towards its basal, pre-stimulus level (more in olfactory transduction than in phototransduction);

  2. 2

    multipulse response: if for short delays between the two pulses the response to the second pulse is attenuated with respect to the first one, as the lag time between the two pulses increases, a progressive growth of the amplitude of the second response is observed, up to a complete recovery;

  3. 3

    double step response (in phototransduction): unlike for a single step, the deactivation phase of the inner step exhibits an overshoot with respect to the steady state value corresponding to the outer step. No significant overshoot is observable for deactivation of the outer step.

It is remarkable that both sensors exhibit input-output responses which are qualitatively similar for what concerns both the types of adaptation mentioned in the introduction.

A minimal regulatory model for input response

Detailed dynamical models for the two sensory systems can be found in Refs. 27,28,17 for olfactory transduction and in e.g. Refs. 29,30,31 for phototransduction. The approach followed in this paper is different: rather that including into our models all the kinetic details available for the two signaling pathways, we would like to introduce an elementary model which, in spite of its extreme simplicity, is nevertheless able to qualitatively capture the salient features of the various responses listed in the previous section. This basic model is presented now in general terms. Later on an interpretation in terms of the specific signaling mechanisms of the two pathways is provided. More specific models tailored to the two transduction processes are discussed in the Supplementary Information.

Consider the 2-variable prototype regulatory system depicted in Figure 1A. It represents a system in which two molecular species y and x are linked by a negative feedback loop. The following minimal mathematical model describes the reactions in the scheme of Figure 1A:

where k1 and k2 are gains and the two parameters δx, δy represent first order degradation rates in y and x. The external stimulus u favors the production of y, which is instead inhibited by the negative feedback from x. In turn, the synthesis of x is enhanced by y. By construction 0 ≤ y ≤ 1 and x ≥ 0, meaning that the model is biologically consistent. The model (1) is the simplest elementary dynamical system having an input-output behavior resembling that of olfactory transduction.

Consider the change of variable z = 1 – y, 0 ≤ z ≤ 1. A straightforward algebraic manipulation allows to rewrite the system (1) in terms of z. In this case the regulatory actions have the opposite sign: u decreases z while the feedback from x promotes the formation of z.

This is the minimal model which will serve as reference for the input-output behavior of phototransduction. By construction, the models (1) and (2) exhibit the same dynamical behavior up to a flipping symmetry in the y and z variables. An exegesis of these models, explaining the role of each of the terms and including other technical details such as shifted baseline levels, is presented in the Supplementary Information. In particular, possible alternative minimal models are formulated and their responses investigated in Supplementary Figure S2 and S3.

Perfect adaptation fails to reproduce multipulse adaptation

While several models exist able to capture perfect step adaptation14,15,20,12,23,24, there is one general principle to which most proposals are equivalent, namely that perfect step adaptation in order to be robust to parametric variations must be obtained by means of a negative regulation and that this regulation achieving perfect step adaptation must be of integral feedback type, see Refs. 24,20. In our minimal models (1) and (2), an integral feedback is obtained when the degradation rate constant for x vanishes i.e., δx = 0. This corresponds to the second differential equation of (1) being formally solvable as the time-varying integral

and analogously for (2). Since y(t) ≥ 0, the integral (3) is monotonically growing in this case, hence the feedback variable keeps growing and stabilizes only when y(t) → 0. Such a behavior occurs regardless of the amplitude of the input step u (note that, when a nonzero baseline level yo is considered in (1), then (3) becomes ; the monotonicity property is preserved for the variation with respect to yo and the steady state imposed by perfect adaptation is y(t) → yo, see Supplementary Information for details). In the engineering analogy of an integrator being a capacitor, y(t) ≥ 0 implies that x(t) gets charged and never discharges. In a double pulse protocol, this implies that after the first pulse x(t) > 0 and when the second pulse arrives the response of the feedback is more prompt because x(t) is already charged. Hence the second pulse response is attenuated with respect to the first. However, lack of degradation of x(t) implies that the behavior occurs regardless of the lag time between the two pulses, which contradicts the experimental results shown in Figure 2B and Figure 3B. Hence a perfect adaptation model is inadequate for our sensory transduction pathways, because i) it fails to reproduce the non-exact return to the prestimulus level observed in the step responses of Figure 2A and Figure 3A and ii) it completely misses the recovery in the multipulse adaptation observed in Figure 2B and Figure 3B.

Reproducing both types of adaptation: a trade-off of time constants

In a model like (1) or (2), both types of adaptation are determined by the ratio between the characteristic time constants of the two kinetics, which are captured with good approximation by the first order kinetic terms (i.e., by δy and δx). The ratio δx/δy modulates the amount of adaptation in opposite ways in the two types of input protocols. If δx = 0 represents perfect step adaptation but recovery from multipulse adaptation is absent, when δx/δy ≪ 1 (i.e., the characteristic time constant of x is much longer than that of y), then step adaptation is almost perfect while multipulse adaptation recovers very slowly. This behavior is similar to what happens in our experiments with the olfactory transduction system shown in Figure 2. When instead δx/δy < 1 but not too far from a ratio of 1, then step adaptation is partial but multipulse adaptation recovers quickly, see again Figure 1. This situation resembles our experiments with phototransduction shown in Figure 3. When instead δx/δy > 1 neither of the two forms of adaptation is visible.

Deactivation and (lack of) undershooting

Upon termination of a step, a response deactivates, meaning in our model (1) that the observable variable y returns to its pre-stimulus level yo (which for simplicity and without loss of generality we are assuming equal to 0). The way it does so is informative of the dynamics of the system. In a system with exact integral feedback, if the activation profile overshoots the baseline and then approaches it again, then the deactivation time course must follow a pattern which is qualitatively similar but flipped with respect to the baseline, i.e., it must undershoot the baseline during the transient, see Model 3 of the Supplementary Information, described in (S3) and Supplementary Figure S2. In models with a high degree of symmetry, like for example in presence of input scale invariance (“fold change detection” of Shoval et al.32), the responses could even have a mirror symmetry around the baseline yo.

The undershooting in the deactivation phase should however be observable experimentally, i.e., it should produce an output current which becomes less than basal in olfactory transduction or higher than basal in phototransduction. No experiment with the olfactory system shows undershooting of the basal current. Also in phototransduction experiments, for both pulse and step responses in dark, no overshooting above the noise level can be observed in the deactivation phase. For both sensors, this behavior is confirmed by many more experiments available in the literature33,34,35,7,29,9.

As discussed more thoroughly in the Supplementary Information, the lack of deactivation undershooting is another element that can be used to rule out the presence of exact integral feedback regulation in our systems.

A double step may instead exhibit undershooting

By construction, the model (1) can never undershoot the baseline since all negative terms in (1a) vanish when y → 0 (the argument is similar for a baseline yo ≠ 0, see (S8)). This is coherent with the step deactivation recordings shown in Figs. 2–3. Assume now that the input protocol consists of a double step as in Figure 4. If y1 is the steady state reached in correspondence of a single step, then necessarily y1 > 0 in our non-perfectly adapting systems. However, even when this single step stimulation is present, the negative feedback in (1a) still maintains the original baseline yo = 0 as reference. It means that when a second step input is superimposed to the first as in Figure 4, it is in principle possible that in the deactivation phase of this second step a transient significantly undershooting the “fictitious” baseline y1 may now appear. This is indeed what happens for the model (1), see Figure 4A. Clearly under perfect adaptation y1 = yo = 0, hence exact integral feedback predicts no difference between the single step and the double step deactivation.

Given the very strong adaptation in olfactory sensory neurons, the double step experiment has been performed only in photoreceptors: indeed the combination of near zero baseline and almost perfect adaptation implies that in olfactory sensory neurons the presence of an overshoot will be hardly detectable. In photoreceptors, instead, the double step deactivation behavior of (1) is faithfully reproduced. In the input protocol, the broader step of smaller amplitude corresponds to a constant dim light on top of which a more intense light step is applied. The current recording shown in Figure 4B indeed exhibits a consistent deactivation overshooting not observed in dark.

Apart from providing a validation of the reliability of the simple model (1), a direct interpretation of this transient is that indeed the system keeps a memory of the basal level “anchored” at yo even when constant stimuli are applied to the system.

Interpretation of the elementary model in the context of olfactory and phototransduction pathways

In this paper we will not attempt to present comprehensive mathematical models of the two sensory pathways containing all the biochemical reactions known to be involved in the signaling transduction of the stimuli, but will limit ourselves to consider the section of the pathways involving the Cyclic Nucleotide-Gated (CNG) channels and a primary calcium-induced feedback regulation. For the olfactory system, the pathway is depicted in Supplementary Figure S4A and the corresponding model in (S9). In our minimalistic approach, in the olfactory system the variable y can be associated to the fraction of open CNG channels on the ciliary membrane. In absence of stimulation, the channels are almost completely closed. Upon arrival of a stimulation, the CNG channels open and the inflow of calcium ions triggers the negative feedback regulation which closes the CNG channels. In a model like (1), the feedback variable x plays the role of the concentration of the calcium-activated protein complexes responsible for the gating of the channels. More details on the reactions considered (and on those omitted), on the set of differential equations used for these reactions and on the fitting of the kinetic parameters are available on the Supplementary Information. The fit resulting from this kinetic model is shown in blue in Figure 2, see also Supplementary Figure S4. Its dynamical behavior is very similar to that of (1), shown in Figure 1B.

Unlike for the olfactory system, in phototransduction the CNG channels are (partially) open in absence of stimulation and they further close when the photoreceptors are hit by an input of light. If we think of z as the fraction of open CNG channels, then the mechanism (2) can be used in phototransduction to describe qualitatively the core action of the primary feedback loop (due to guanylate cyclase). In the response to light, in fact, its effect is to reactivate z. Also for this system a thorough description of the dynamical model and of its kinetic details is provided in the Supplementary Information. The resulting fit for the phototransduction experiments is the blue traces of Figures 3 and 4B. Other details are in Supplementary Figure S5. Also in this case the core dynamical behavior of the pathway-specific model (S11) and that of the elementary model (2) resemble considerably. For phototransduction, more complex input protocols than those discussed here are possible and are sometimes discussed in the literature36. As an example, the response of both models (S9) and (S11) to a train of identical equispaced pulses is commented in the Supplementary Information and in Figure S6.

Discussion

To date, the vast majority of papers dealing with models for sensory adaptation has focused on the perfect step adaptation case11,12,14,15,18,19,20,21,22,23,32. While in some examples of sensory response, like in E.coli chemotaxis, perfect step adaptation may reasonably well describe the motility response of the bacterium, in many other case studies (notably in sensory systems of higher organisms) the classification as perfect adapters holds only as long as the sensor “as a whole” is considered. These sensorial responses are however much more complex cognitive processes than the single cell signaling transductions considered in this paper and have little to do with the models (and data) discussed in the paper. For example, the visual system can adapt over light variations of several orders of magnitude. However, when looking at single photoreceptors, if cones virtually never saturate in response to steady illumination2,37, the capacity of rods (the receptors studied in this paper) to adapt is much more modest and this can already be seen in the partial step adaptation of Figure 3A. When it comes to modeling adaptation, an emblematic example of the difference between an omnicomprehensive sensory system and the single cell level of interest here is given by a “sniffer”, i.e., a basic circuit (an incoherent feedforward loop) often considered as a model for perfect adaptation and sometimes taken as paradigm for the functioning of the sense of smell “as a whole” on a purely phenomenological basis23,22,32. This model not only can adapt perfectly, but it can do so without any feedback loop. If experiments such as those of Figure 2 show that at the level of single receptor step adaptation is not exact, other experiments in low-calcium show that when the (calcium-induced) feedback regulation is impaired, adaptation basically disappears and even a single pulse response terminates very slowly (see e.g. Refs. 33 and Supplementary Figure 8 of De Palo et al.17). This implies that feedback regulation is crucial for adaptation in our olfactory neurons. As similar arguments hold also for phototransduction, in this paper incoherent feedforward mechanisms are never considered as potential models for adaptation (perfect or less).

Even though the distinction between perfect and partial step adaptation has been known for a while11, the dynamical implications of the different models for other input protocols has in our knowledge never been investigated in detail. In this paper we show that not only this difference is observable in several experimental features of the responses, but also that it has important conceptual consequences. One of these consequences is that in a system with a perfectly adapting mechanism modeled with an exact integral feedback the basal working value of the state is “internal” and uncorrelated with the environment. While this allows the system to climb exactly any step of input (all steps have the same steady state yo), it implies that the transient responses during stimulus activation and termination should have similar (but specular with respect to a baseline level) profiles as in Model 3 of Supplementary Figure S2. On the contrary, in a sensor with a partial step adaptation mechanism, the steady states reached in the step responses depend on the amplitude of the step, while instead the feedback remains “anchored” around the basal level yo, itself uniquely associated to an input amplitude (which could be u = 0 in the simplest case). This implies that while weberian-type graded responses for the peaks of the transients are still possible2, properties involving the whole profile of the response such as the input scale invariance of Refs. 32 are no longer possible, not even approximately. Our double step experiment with its asymmetry in the two deactivation phases clearly shows that such an input invariance cannot hold not even qualitatively for our sensors. Furthermore, anchoring the state around a nominal input value helps shifting the dynamical range back to that value when the stimulus terminates, resetting the sensor to the most plausible value of the environment without incurring into unrealistic deactivation transients.

Another important difference between the dynamical models of perfect and partial adaptation concerns the effect on internal, nonobservable variables like our x in (1). Exact integral implies an infinite time constant for x (or, in practice, longer that the time scales of interest for the observable kinetics). Partial step adaptation, instead, is associated to changes in x which are still slower than those observed on the output of the system, but not by orders of magnitude. How much slower these changes are influences how much adaptation we observe in the step responses. Experiments with time-varying input protocols, namely with double pulse sequences, allow to have a rough estimate of the slower time constant. In olfactory transduction, this time constant is normally associated to the shift in dose-response plots (which is an alternative, compatible, way to describe the multipulse adaptation effect, see Supplementary Figure 6 of De Palo et al.17). What is predicted by theoretical models and confirmed by experiments is that the speed of the recovery in multipulse adaptation is inversely correlated to the amount of step adaptation. In particular, for the two sensors investigated in this work the relative amount of the two forms of adaptation are different.

From a physiological perspective, this difference can be interpreted in terms of the different dynamical ranges in which the two sensors are required to operate. The visual system of vertebrates operates over a range of light intensities spanning 6–10 orders of magnitudes thanks to the presence of two kinds of photoreceptors, rods and cones and to their adaptation properties7,8,2. The olfactory system is capable of detecting very low concentrations of odorants, but has a less broad dynamical range38,39. A faint olfactory stimulation is properly detected, but very often its perception rapidly fades away and is not perceived any more, while a visual stimulation with a faint contrast is perceived and its perception remains. These basic properties of vision and olfaction are the result of a complex and sophisticated signal processing occurring in the visual and olfactory systems but are also in part determined by what occurs at the receptor level.

Vertebrate photoreceptors respond to light with a membrane hyperpolarization and this hyperpolarization is transformed in the retina into a train of spikes sent to higher visual centers40. In order to operate properly over an extended range of light intensities, photoreceptors must have only a partial adaptation. Olfactory sensory neurons, in contrast, respond to odors by a membrane depolarization evoking trains of spikes5 and, in order to respond to faint odors only transiently, they must have an almost perfect step adaptation.

Photoreceptors and olfactory sensory neurons differ also in another important aspect: in the absence of sensory stimulation the membrane resistance of olfactory sensory neurons is very high (in the order of GΩ) and decreases in the presence of the appropriate odorants. Indeed, olfactory sensory neurons can fire an action potential as the consequence of the opening of a single channel41. Therefore it is more convenient for olfactory sensory neurons to have an almost perfect adaptation. Photoreceptors, in contrast, have a high membrane conductance in darkness which decreases with the illumination42 and do not need a perfect adaptation to extend their dynamic range.

It is worth remarking that for both sensors the steady state values for partial step adaptation and the time constants for recovery in multipulse adaptation that we deduce from the experiments are coherent with the trade-off proposed in the paper. The main prerequisite for this trade-off to be well-posed, namely that the system in the deactivation phase obeys approximately a linear decay law, is the same mechanism that enables the reset of the output to the pre-stimulus baseline without undershooting this nominal value. This property of the model is confirmed in the experiments. Also the more fine-graded prediction that, upon perturbation of the natural decay law by means of an altered baseline level, the deactivation transient can become less regular (and undershooting can appear) is validated by our double pulse experiments.

Methods

Olfactory transduction

Olfactory sensory neurons have been dissociated from the Ambystoma Tigrinum salamander as previously reported43,17. Only neurons with clearly visible cilia were selected for the experiments. The currents were elicited by the application of 0.1 mM IBMX (3-isobutil-1-methylxanthine, a phosphodiesterase inhibitor permeable to the cellular membrane), previously dissolved in DMSO at 100 mM and then diluted in a Ringer solution in order to obtain the final concentration value. The release of IBMX to the neurons was performed through a glass micropipette by pressure ejection (Picospritzer, Intracel, United Kingdom). All experiments were performed at room temperature (22–24°C). Transduction currents on the surface of the dissociated neurons were measured through whole-cell voltage clamp recordings (as described in Refs.1,43,44) where the holding potential corresponds to −50 mV. All experiments were carried out in accordance with the Italian Guidelines for the Use of Laboratory Animals (Decreto Legislativo 27/01/1992, no. 116).

Phototransduction

Isolated photoreceptors from retina: dissociated rods were obtained using adult male Xenopus laevis frogs as previously reported45,46,47. All experiments carried out have been approved by the SISSA's Ethics Committee according to the Italian and European guidelines for animal care (d.l. 116/92; 86/609/C.E.). The frogs were dark-adapted and the eyes were enucleated and emisected under a dissecting microscope with infrared illumination (wavelength 820 nm); isolated and intact rods were obtained by repeatedly dipping small pieces of retina into a Sylgard Petri dish with a Ringer solution containing the following (in mM): 110 NaCl, 2.5. KCl, 1 CaCl2, 1.6 MgCl2 and 3 HEPES-NaOH, 0.01 EDTA and 10 Glucose (pH 7.7–7.8 buffered with NaOH). After dissociation the sample was transferred into a silanized recording chamber containing the Ringer solution. All experiments were performed at room temperature (22–24°C).

Electrophysiological recordings: after the mechanical isolation, the external (or the internal) segment of an isolated and intact rod was drawn into a silane-coated borosilicate glass electrode (internal diameter of 6–8 μm) filled with Ringer solution. The cell was viewed under infrared light (wavelength 900 nm) and stimulated with 491 nm diffuse light (Rapp OptoElectronic, Hamburg, Germany). The photocurrents obtained after the stimulus where recorded using the suction-electrode recordings, as previously described45,29, in voltage-clamp conditions and achieved with an Axopatch 200A (Molecular Devices). The functionality of the cell was confirmed by the observation of the amplitude of the cell response (typically 15–20 pA) to brief light flashes (1 ms) of saturation intensity. Different light stimuli protocols were used for different recordings (see figure legends).