Abstract
Collective animal behaviour occurs at nearly every biological size scale, from single-celled organisms to the largest animals on earth. It has long been known that models with simple interaction rules can reproduce qualitative features of this complex behaviour. But determining whether these models accurately capture the biology requires data from real animals, which has historically been difficult to obtain. Here, we report three-dimensional, time-resolved measurements of the positions, velocities and accelerations of individual insects in laboratory swarms of the midge Chironomus riparius. Even though the swarms do not show an overall polarisation, we find statistical evidence for local clusters of correlated motion. We also show that the swarms display an effective large-scale potential that keeps individuals bound together and we characterize the shape of this potential. Our results provide quantitative data against which the emergent characteristics of animal aggregation models can be benchmarked.
Similar content being viewed by others
Introduction
Spontaneous, collective biological activity—in swarms, flocks, schools, herds, or crowds—has evolved independently across the entire biological size spectrum, from single cells1,2,3 to insects4, birds5,6, or fish7,8,9. Nature has found such self-organized behaviour to be a robust, simple solution to a broad range of biological problems.
The ubiquity of emergent collective behaviour suggests that it may arise from relatively simple interactions between individuals—and indeed, a vast literature on modelling animal aggregations has developed over the past few decades. Models with simple rules have been shown to reproduce, at least qualitatively, patterns and behaviours observed in the wild, including bulk alignment or polarisation10, milling11, swarming12, aggregation13 and predator avoidance14. Both continuum15 and discrete16 models can produce results that resemble observational data.
But qualitatively matching the large-scale emergent behaviour does not demonstrate that a model correctly captures the biology17,18; instead, detailed, quantitative comparisons with actual data are required. In recent years, such data have begun to become available, particularly for animals that move only in two dimensions4,19,20 or three-dimensional groups of a few individuals7,21,22,23,24,25,26. A recent landmark study from the STARFLAG group imaged and tracked wild flocks of starlings numbering in the thousands5,6,27,28,29, by far the largest groups of collectively moving animals measured to date. Due to the difficulties inherent to fieldwork, however, the temporal range and resolution of this work was limited; thus, the STARFLAG group focused on flock shape measurements and single-time velocity statistics27,29. Making more progress on understanding and modelling collective animal behaviour requires measurements of animal aggregations that simultaneously resolve the dynamics of the entire group (typically over large length scales and slow time scales) as well as the kinematics and history of motion of each individual in the group (typically over short length scales and fast time scales).
Recent developments in high-speed imaging for fluid dynamics and turbulence, where the challenge of accurately measuring dynamics over wide ranges of length and time scales is likewise unavoidable30, have now made such measurements possible. Here, using experimental tools originally developed to study turbulent flows, we report three-dimensional, high-speed measurements of the positions, velocities and accelerations of all the individual members of laboratory swarms of Chironomus riparius midges. We find, as expected, that the group dynamics of our swarms are qualitatively different from bird flocks and fish schools, as characterized by the overall group shape, isotropy of acceleration and bulk polarisation. But we also find evidence that local clusters of correlated motion may exist, as suggested by the presence of long tails in the speed distribution and by measurements of the spatial statistics of the midges. At large scales, we show that the swarms display an effective potential well that keeps the individual insects bound to it; the shape of this well, however, depends on how it is measured. Our results provide data that can be used to benchmark swarm models quantitatively and that advance our fundamental understanding of collective animal behaviour.
Results
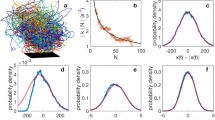
We established a self-sustaining laboratory colony of C. riparius midges using egg masses purchased from Environmental Consulting and Testing, Inc. C. riparius is an attractive organism for this work because it is available commercially, is relatively straightforward to maintain31,32,33 (our husbandry procedures are described in the methods section) and has been observed to swarm in captivity much as it does in the wild34,35. We image the mating swarms (also known as leks) using three synchronized high-speed cameras, as sketched in Fig. 1. By exploiting the redundant information recorded by the cameras36, we extract the three-dimensional positions of each individual in the swarm. We measure locations in a Cartesian coordinate system (x, y, z), where the z direction points upward and the origin is at the swarm's centre of mass. Using a predictive particle tracking algorithm developed to study intense turbulence36 (described briefly in the methods section), we then record the motion of individual midges through time. Figure 1 shows both a snapshot of a swarm and the prior history of each individual.
Snapshot of a swarm and experimental arrangement.
(a–c) Snapshots from each of the three synchronized cameras (left, center and right, respectively) focused on a common volume near the center of the swarm. Regions identified as midges are coloured red. (d) The experimental arrangement, seen from above and drawn to scale. Swarming midges remain far from container boundaries. (e) The corresponding three-dimensional snapshot. An arrow indicates the location of each tracked midge; the arrow lengths are proportional to speed and their orientations indicate flight direction. (f) The same snapshot, with each individual's current position indicated by a dot and past flight path indicated by a curve.
Swarm spatial structure
Since we track each individual midge, we can quantify the three-dimensional spatial structure of their collective motion. Figure 2a shows the distributions of the distance from each individual to the swarm centre, defined as r = (x2 + y2 + z2)1/2, measured for ten different swarms. By normalising by the mean swarm radius Rs = 〈r〉, we find that the shape of the distribution is similar for all ten swarms, even though their sizes vary. As shown in Fig. 2b, Rs itself scales as Rs ∝ 〈N〉1/3, where 〈N〉 is the average number of individuals in the swarm, suggesting that the number density of midges in the swarm is approximately fixed. We note that this result is different from what has been observed for bird flocks, where the number density can fluctuate enormously from flock to flock27.
Swarm shape statistics.
(a) Distribution of the distances r of each individual from the swarm centre, normalised by the swarm size Rs. Each curve shows data for one swarm and these volumetric probabilities P satisfy  . (b) Swarm size as a function of mean swarm population. Each data point is computed as the average over the entire time of observation and the ellipses show the standard deviation. Note that the number of individuals in each swarm is not fixed, since midges may enter or leave the swarm during the measurement period. Marker colours correspond to curve colours in (a). The dashed curve is a Rs ∝ 〈N〉1/3 fit, as would be expected if the number density were independent of the swarm size. For the largest swarms, some of the midges flew outside the region imaged by the cameras; in these cases, the markers are outlined in grey. (c) Swarm aspect ratio as a function of swarm size. (d) Bulk swarm orientation. One axis of each swarm nearly aligns with gravity; for large swarms, it is the axis along which the swarm is longest, e1. (e) Spatial variation of swarm density. Slices through the three-dimensional probability density function of midge position are shown in colour on a logarithmic scale for the swarm marked with a black arrow in (b).
. (b) Swarm size as a function of mean swarm population. Each data point is computed as the average over the entire time of observation and the ellipses show the standard deviation. Note that the number of individuals in each swarm is not fixed, since midges may enter or leave the swarm during the measurement period. Marker colours correspond to curve colours in (a). The dashed curve is a Rs ∝ 〈N〉1/3 fit, as would be expected if the number density were independent of the swarm size. For the largest swarms, some of the midges flew outside the region imaged by the cameras; in these cases, the markers are outlined in grey. (c) Swarm aspect ratio as a function of swarm size. (d) Bulk swarm orientation. One axis of each swarm nearly aligns with gravity; for large swarms, it is the axis along which the swarm is longest, e1. (e) Spatial variation of swarm density. Slices through the three-dimensional probability density function of midge position are shown in colour on a logarithmic scale for the swarm marked with a black arrow in (b).
To characterize the swarm shape in more detail, we calculated the inertia tensor for each swarm. The eigenvectors e1, e2 and e3 specify the intrinsic orientation of the swarm and the standard deviations I1, I2 and I3 (labelled in decreasing order) of individual midge positions along these eigenvectors give a measure of the swarm size in each direction. In Fig. 2c, we show the aspect ratios I1/I2 and I1/I3 for our measured swarms. Our swarms tend to have one dimension that is somewhat shorter than the other two, which are comparable; but unlike, for example, bird flocks27, all three dimensions are fairly similar. Our swarms are thus weakly axisymmetric. To quantify the overall swarm orientation, we measured the angles θ1, θ2 and θ3 between the direction of gravity and each eigenvector. As shown in Fig. 2d, all of our swarms have one eigenvector that is nearly vertical; note that we plot cosθi rather than θi itself, since cosθi is uniformly distributed for random angles37. This vertical eigenvector corresponds to the longest dimension of the swarm for large swarms, but surprisingly to the intermediate dimension for smaller swarms. The origin of this effect is unclear; it may be that individuals join the swarm by flying above it, thereby extending large swarms in the vertical direction. More details of swarm shape are revealed by plotting slices through the full three-dimensional probability density function (PDF) of midge position, as shown in Fig 2e for a single swarm; midges are found most often in red regions and least often in blue ones. Consistent with our observations of aspect ratios, the long axis of this swarm is nearly vertical. Finally, let us note that our swarms do not fill the entire laboratory enclosure; the midges remain far from the walls and the shape of the swarm is an emergent property.
Velocity statistics
Since we track individual midges over long times, we can measure the individual, instantaneous three-dimensional velocity v and acceleration a of each. We find that the swarms are roughly fixed in space and so the mean velocity is nearly zero; the fluctuations, however, are not. Figure 3a shows the standard deviation of the vertical velocity component (σvz) and one horizontal velocity component (σvx); the other horizontal component is statistically the same, as expected given that the horizontal orientation of our coordinate system is arbitrary. Individual midges tend to fly faster horizontally than vertically, since σvx exceeds σvz by about 50% in all cases. It has been argued on aerodynamic grounds that near-horizontal flight should be most efficient for birds38 and observations of starling flocks confirm this behaviour27. Our observations of the flight paths of individual midges (see, for example, Fig. 1c) show a similar preference, even though the Reynolds number for the flying midges and therefore the aerodynamic regime, is quite different. But despite this similar tendency of individual midges to fly horizontally, our swarms do not show an overall polarisation, as shown in Fig. 3b. Here polarisation is defined12 as  , where N is the number of individuals, vi is the velocity of an individual and 0 ≤ p ≤ 1. Our swarms have p ≤ 0.09 in all cases, whereas bird flocks, for example, have been found to have p near unity29. On the average, unlike bird flocks and fish schools, midges have little tendency to align with their neighbours.
, where N is the number of individuals, vi is the velocity of an individual and 0 ≤ p ≤ 1. Our swarms have p ≤ 0.09 in all cases, whereas bird flocks, for example, have been found to have p near unity29. On the average, unlike bird flocks and fish schools, midges have little tendency to align with their neighbours.
Statistics of individual midge velocities.
(a) Standard deviations of swarm velocity components; note that the mean velocity in all directions is nearly zero. Typical horizontal velocities, as measured by these standard deviations, exceed vertical velocities, perhaps improving flight efficiency. (b) Polarisation p is near zero for all swarms observed, distinguishing swarming behaviour from flocking and schooling. (c, d) Standardised velocity distributions along (c) the vertical direction and (d) one horizontal direction. The distributions are nearly Gaussian (a reference Gaussian curve is shown in grey), with slight deviations in the tails. (e) Standardised speed distributions, with the standardised Maxwell–Boltzmann distribution shown in grey for comparison. A heavy, nearly exponential tail develops for large swarms, which may indicate the formation of clusters.
In addition to the statistical moments of the velocity, we can also measure its full PDF; velocity PDFs for all ten swarms measured are shown in Fig. 3c–e. In all cases, we plot the PDFs of the standardised velocities  , where vi is the ith component of the velocity. We note that the mean velocities 〈vi〉 are all nearly zero. The standardised PDFs of both the horizontal and vertical velocities have similar, nearly Gaussian shapes near their cores, with tails that deviate slightly from Gaussian values. This trend is more clear when we plot the PDF of the standardised speed
, where vi is the ith component of the velocity. We note that the mean velocities 〈vi〉 are all nearly zero. The standardised PDFs of both the horizontal and vertical velocities have similar, nearly Gaussian shapes near their cores, with tails that deviate slightly from Gaussian values. This trend is more clear when we plot the PDF of the standardised speed  , as shown in Fig. 3e. There, we compare the swarm data with the Maxwell-Boltzmann distribution for the speeds of a hard-sphere gas in thermal equilibrium, since a previous, pioneering study of midge swarming found results consistent with Maxwell-Boltzmann statistics for small swarms21. Our smallest swarms agree well with Maxwell-Boltzmann statistics; for our larger swarms, however, the speed distributions show a long, nearly exponential tail that grows monotonically with swarm size.
, as shown in Fig. 3e. There, we compare the swarm data with the Maxwell-Boltzmann distribution for the speeds of a hard-sphere gas in thermal equilibrium, since a previous, pioneering study of midge swarming found results consistent with Maxwell-Boltzmann statistics for small swarms21. Our smallest swarms agree well with Maxwell-Boltzmann statistics; for our larger swarms, however, the speed distributions show a long, nearly exponential tail that grows monotonically with swarm size.
One possible origin for the long tails we observe in the speed distributions is clustering; that is, a highly non-uniform distribution of the individual midges in space. This effect and the corresponding long tails, have been observed, for example, in hard-sphere granular gases39. To look for evidence of statistical clustering in our swarms, we calculated the distance dnn from each individual to its nearest neighbour. The root-mean-square nearest-neighbour distance  is shown for each swarm in Fig. 4a and tends to decrease as swarms grow more populous. For a given number density,
is shown for each swarm in Fig. 4a and tends to decrease as swarms grow more populous. For a given number density,  is largest when individuals arrange themselves uniformly in space;
is largest when individuals arrange themselves uniformly in space;  shrinks as individuals cluster more and more. The corresponding standardised PDFs are shown in Fig. 4b and the statistical signature of clustering should be deviations of these data from similar calculations for uniformly distributed particles. Thus, we also computed nearest-neighbour distances for simulated data where we fixed the number of particles N and overall size of the domain Rs to be the same as those measured for the swarms but distributed the particles randomly in space. The resulting data are included in Fig. 4. Comparing, we find that the distributions for the swarms are wider than for the simulated data, implying that nearest-neighbour distance fluctuates more strongly in the swarms. The peaks of the distributions, however, lie at somewhat smaller distances for the swarms than for the random particles, so that the midges in our swarms are typically slightly closer to their neighbours than the randomly placed particles are.
shrinks as individuals cluster more and more. The corresponding standardised PDFs are shown in Fig. 4b and the statistical signature of clustering should be deviations of these data from similar calculations for uniformly distributed particles. Thus, we also computed nearest-neighbour distances for simulated data where we fixed the number of particles N and overall size of the domain Rs to be the same as those measured for the swarms but distributed the particles randomly in space. The resulting data are included in Fig. 4. Comparing, we find that the distributions for the swarms are wider than for the simulated data, implying that nearest-neighbour distance fluctuates more strongly in the swarms. The peaks of the distributions, however, lie at somewhat smaller distances for the swarms than for the random particles, so that the midges in our swarms are typically slightly closer to their neighbours than the randomly placed particles are.
Distance to nearest neighbours.
(a) Root-mean-square nearest-neighbour distance  for midge swarms and randomly distributed particles, shown as circles and squares, respectively. The data follow the same trend for each data set, but
for midge swarms and randomly distributed particles, shown as circles and squares, respectively. The data follow the same trend for each data set, but  is always larger for real swarms. (b) Standardised PDFs of dnn for measured swarms (upper) and randomly positioned particles (lower); note that the lower curves have been vertically offset for clarity. Each curve shows data for one swarm. The most probable dnn is smaller for the swarms than for the random particles, (see also (c), which shows the same plots on linear axes), but the swarms also show a much longer tail, indicating larger voids.
is always larger for real swarms. (b) Standardised PDFs of dnn for measured swarms (upper) and randomly positioned particles (lower); note that the lower curves have been vertically offset for clarity. Each curve shows data for one swarm. The most probable dnn is smaller for the swarms than for the random particles, (see also (c), which shows the same plots on linear axes), but the swarms also show a much longer tail, indicating larger voids.
Acceleration statistics
In addition to measuring position and velocity, we image the midges in the swarm rapidly enough that we can measure their instantaneous accelerations. Since the acceleration of an individual midge is directly proportional to the net force acting on it, acceleration measurements provide a useful way to begin to relate kinematics to dynamics; that is, we can consider the measured accelerations to be effective net forces on the midges. In Fig. 5a, we plot the standard deviations σaz and σax of the accelerations in the vertical and horizontal directions, respectively; we show only one horizontal component since the swarm statistics are empirically axisymmetric. These two standard deviations are nearly equal, showing no signs of any anisotropy due to gravity. In Fig. 5b,c, we show the full standardised PDFs of these acceleration components. The PDFs in both directions show very heavy tails compared with Gaussian distributions, as is commonly observed in strongly correlated fluid flows40,41. The shape of the PDFs in the two directions is similar, although the tails are somewhat heavier in the horizontal plane.
Statistics of individual midge accelerations.
(a) Standard deviations of acceleration components as a function of swarm size. Horizontal and vertical accelerations are nearly identical in magnitude for all the observed swarms. (b,c) Standardised acceleration PDFs, for (b) the vertical and (c) horizontal directions. (d) Standard deviations of acceleration parallel and perpendicular to the instantaneous direction of flight. The two components are again nearly identical. (e,f) Standardised PDFs of acceleration parallel (e) and perpendicular (f) to the direction of flight.
Given that acceleration statistics are nearly isotropic in the laboratory frame, one might ask whether that isotropy extends to the animals' own frames of reference. We therefore studied the statistics of acceleration in a coordinate system fixed to each individual midge, measuring the acceleration parallel to the direction of flight (that is, along the velocity vector) and perpendicular to it. In Fig. 5d, we plot the standard deviations of these two acceleration components. We see no appreciable difference between the two, again suggesting that the fluctuations in acceleration are isotropic and independent of reference frame. In particular, this result shows that (statistically) the midges show no preference for turning (which requires accelerating normal to the velocity vector) over speeding up or slowing down, or vice versa. This observation is borne out by measurements of the full PDFs of parallel and perpendicular acceleration, shown in Fig. 5e,f. This measured isotropy contrasts with observations for directed groups of birds or fish, where acceleration depends strongly on the direction of motion42. This result is surely partially due to the smaller size and inertia and therefore enhanced manoeuverability, of midges as compared with birds or fish, but is also likely indicative of the different group dynamics.
Spatial structure of acceleration
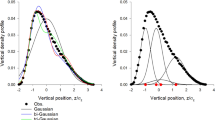
Since we resolve the trajectories of each midge individually, we can probe the swarm dynamics with more detail by studying how the acceleration of the midges depends on their location inside the swarm. In Fig. 6a, we show the mean vertical acceleration conditioned on vertical position; similarly, Fig. 6b shows the mean horizontal acceleration conditioned on horizontal position. For both directions, the accelerations vary systematically with position in the swarm. On the average, midges above the centre of the swarm accelerate downwards, while midges below the centre accelerate upwards. A similar trend of acceleration towards the swarm centre is clear—and stronger— in the horizontal direction. Functionally, acceleration toward the centre keeps the swarm intact: midges tend to adjust their flight direction to point back towards the swarm. Moreover, the conditional acceleration increases linearly as the distance from the swarm centre increases. Taking this conditional acceleration as an effective force24, the individuals in the swarm behave on the average as if they are trapped in an elastic potential well (since the effective force is linear in position) that keeps them bound to the swarm. This result is consistent with earlier, less well resolved observations22.
Mean acceleration as a function of position.
(a,b) Mean acceleration conditioned on position in (a) the vertical direction and (b) one horizontal direction. The conditional acceleration varies linearly with a negative slope as a function of position. (c,d) Effective “spring constants” extracted from linear fits to the data in (a) and (b). The effective elastic potentials are stiffer in both directions for smaller swarms. (e) Mean-squared displacement as a function of time averaged over all midges. The dashed line indicates a t2 power law and the data (solid) follow that trend, implying ballistic flight. This power law breaks down only at the swarm edges.
To characterize the effective forces we observed, we fit the data in Fig. 6a,b with straight lines and extracted their slopes. We plot these “spring constants” k as a function of swarm size in Fig. 6c,d for the vertical and horizontal directions. In both cases, the stiffness of the effective elastic potential decreases linearly as the swarms become larger; we also find that the swarms are significantly stiffer in the horizontal direction than in the vertical direction. Midges behave as if they are more weakly bound for larger swarms.
These conditional acceleration measurements suggest that the effective potential binding the swarm together is quadratic, since the effective force is linear in distance from the swarm centre. But acceleration measurements are not the only way to estimate the largescale binding forces. We also studied the transport statistics of individual midges, since we have records of their time-resolved trajectories. In Fig. 6e, we plot the mean-squared displacement 〈d2〉 of midges from their (arbitrary) initial position to their final position; the average is taken over all the midge trajectories we measure in a given swarm. We find that 〈d2〉 grows like a power law in time for more than an order of magnitude, until t ≈ 0.5 s; in fact, 〈d2〉 ~ t2, indicative of ballistic motion where distance scales like time. This ballistic t2 growth saturates when  ; that is, when the average midge has reached the edge of the swarm. Thus, these transport measurements suggest that the individuals in the swarm behave like particles in a square-well potential: they are free until they hit the wall. These measurements differ on the whole from random-walk models43, though such models would apply in the transition away from ballistic motion at the swarm edge. Taken together with our conditional acceleration measurements, our results suggest the emergence of an effective potential well that binds individuals to the swarm. Inside the swarm, however, interactions appear to be statistically rare, so that the individual midges behave to lowest order as if they are freely moving particles. Statistical signatures of their interactions may appear in higher-order transport statistics, but significantly more data will be required to see them. Nevertheless, these results give quantitative observations that can be compared with the output of swarming models.
; that is, when the average midge has reached the edge of the swarm. Thus, these transport measurements suggest that the individuals in the swarm behave like particles in a square-well potential: they are free until they hit the wall. These measurements differ on the whole from random-walk models43, though such models would apply in the transition away from ballistic motion at the swarm edge. Taken together with our conditional acceleration measurements, our results suggest the emergence of an effective potential well that binds individuals to the swarm. Inside the swarm, however, interactions appear to be statistically rare, so that the individual midges behave to lowest order as if they are freely moving particles. Statistical signatures of their interactions may appear in higher-order transport statistics, but significantly more data will be required to see them. Nevertheless, these results give quantitative observations that can be compared with the output of swarming models.
Discussion
In order to gain quantitative insight into the kinematics and dynamics of collective animal behaviour, we measured the individual three-dimensional positions, velocities and accelerations of swarming C. riparius midges. Since our midge colony is maintained in the laboratory, we were able to acquire large amounts of data for many swarming events of different sizes.
As expected, simple position and velocity measures such as polarisation and overall swarm aspect ratio confirmed that swarms are qualitatively different from directed animal groups like bird flocks or fish schools. But our measurement tools also allowed us to perform a more detailed analysis. We observed heavy tails in the speed distributions, suggesting the formation of local, more correlated clusters of midges, particularly for larger swarms. Further evidence for clusters was found by comparing the statistics of the spatial arrangement of midges with randomly positioned particles. Though they are only statistical, these observations suggest that swarms may be more dynamically complex than directed animal groups, which show a strong overall polarisation. For flocks or schools, essentially two length scales are relevant: the inter-individual distance, which controls the local interactions and the overall size of the aggregation, which is an emergent property. This characterization is consistent with, for example, the observation of scale-free velocity correlations in starling flocks29. But clusters in midge swarms would suggest a broader range of important length scales: in addition to the local interaction scale and the overall swarm size, intermediate length scales characterizing these dynamical clusters may also emerge. We anticipate that these “sub-swarms” will be a fruitful topic for further study and are working toward an objective way to define them, so they can be studied individually as well as statistically.
Finally, our measurements of conditional acceleration and of midge displacement suggest the emergence of an overall, large-scale potential that keeps individuals bound to the swarm. Although both of these measures give evidence for an effective potential well, they give different characterizations of the shape of this well. Further study is needed to reconcile these two apparently different results. But, in the short term, these observations give a quantitative characterization of the emergent dynamics of insect swarms that can be used to benchmark swarming models. And, more fundamentally, our data and results add to the growing understanding of collective biological behaviour in nature.
Methods
Insect husbandry
We maintain our colony of C. riparius midges in a transparent 91-cm cubical enclosure kept at 23°C by the laboratory climate control system. The midge enclosure is illuminated on a timed circadian cycle with 16 hours of light and 8 hours of darkness per day. The C. riparius larvae develop in 9 tanks, sketched in grey in Fig. 1a, filled with dechlorinated tap water and outfitted with bubbling air supplies to ensure that the water is sufficiently oxygenated. We provide a cellulose substrate into which the larvae can burrow. The water is cleaned twice a week; after cleaning, the midge larvae are fed crushed, commercially purchased rabbit food. In the last few days of their life cycle, larvae emerge out of the water and become flying adults.
Imaging
Male C. riparius midges swarm spontaneously at dusk as part of their mating ritual. In order to position the swarms in the field of view of our cameras, we use a black plastic “swarm marker” that simulates the river edges where these midges live in the wild35; swarms form above this marker. We film the swarms with three hardware-synchronized 1-megapixel cameras (Photron Fastcam-SA5) at 125 frames per second. The midges are illuminated in the near infrared using 20 LED lamps that draw roughly 3 W of power each; infrared light is invisible to the midges and so will not disturb their natural behaviour, but is detectable by our cameras. The swarms reported here are substantially smaller (typically 20–30 cm on edge; see Fig. 1d–f) than the 91-cm cubical enclosure, to avoid boundary effects.
The cameras are arranged in a horizontal plane on three tripods, as sketched in Fig. 1, with angular separations of 30° and 70°. To calibrate the imaging system, we assume a standard pinhole camera model44. The camera parameters are determined by fits to images of a calibration target consisting of a regular dot pattern45. The calibration target is removed before swarming begins. Roughly 5400 frames of data were recorded for each swarming event.
Tracking individual midges
To track the motion of individuals in the swarm, we first located the midges on each 2D camera frame by finding the centroids of regions that had sufficient contrast with the background and were larger than an appropriate threshold size46. After identification, the 2D locations determined from each camera were stereomatched together by projecting their coordinates along a line in 3D space using the calibrated camera models and looking for (near) intersections36. For the results presented here, we have conservatively only considered midges that were seen unambiguously by all three cameras. Although in principle two views are sufficient for stereoimaging, in practice at least three cameras are typically required to resolve ambiguities and avoid false identifications36. Arranging all three cameras in a plane, as we have done here, can still leave some residual ambiguity; this situation, however, occurs extremely infrequently and is more than compensated for by the simpler and superior camera calibration that can be obtained when all the cameras are positioned orthogonally to the walls of the midge enclosure.
Once the 3D positions of the midges have been determined at every time step, they are linked in time to generate trajectories using a three-frame predictive particle tracking algorithm that has been shown to perform well even in intensely turbulent fluid flow. The tracking algorithm has been described in detail elsewhere36,47 and sample code for a two-dimensional version is available online46. Briefly, at every time step, the expected position of the midge is estimated using the prior history of its motion; located midges at subsequent times that are near these estimates are taken to be good candidates for extending the trajectories. We note that since our swarms are dilute, tracking is relatively easy for these data sets; on average, 97.2% to 99.6% of the trajectories were extended at each time step, depending on the swarm. The total number of midges identified per frame varies from 12 to 111, giving us data sets that range from 6.5 × 104 to 6.0 × 105 total samples. Finally, we compute velocities and accelerations from the midge trajectories by convolving them with a differentiated Gaussian kernel that both smooths the data and differentiates it48. We use several data points to compute each velocity and acceleration, so that our results are more accurate than simple low-order finite differences49. These methods have been proved robust for the much harder problem of measuring the statistics of particles advected by highly turbulent flows and are certainly sufficient for measuring the midge velocities and accelerations. Sample midge trajectories along with traces of the velocity and acceleration are shown for reference as Supplementary Fig. S1 online.
References
Angelini, T. E., Hannezo, E., Trepat, X., Marquez, M., Fredberg, J. J. & Weitz, D. A. Glass-like dynamics of collective cell migration. Proc. Natl. Acad. Sci. USA 108(12), 4714–4719 (2011).
Cisneros, L. H., Kessler, J. O., Ganguly, S. & Goldstein, R. E. Dynamics of swimming bacteria: Transition to directional order at high concentration. Phys. Rev. E 83(6), 061907 (2011).
Chen, X., Dong, X., Be'er, A., Swinney, H. L. & Zhang, H. P. Scale-invariant correlations in dynamic bacterial clusters. Phys. Rev. Lett. 108, 148101 (2012).
Buhl, J., Sumpter, D. J. T., Couzin, I. D., Hale, J. J., Despland, E., Miller, E. R. & Simpson, S. J. From disorder to order in marching locusts. Science 312, 1402–1406 (2006).
Cavagna, A., Giardina, I., Orlandi, A., Parisi, G., Procaccini, A., Viale, M. & Zdravkovic, V. The STARFLAG handbook on collective animal behaviour: 1. Empirical methods. Anim. Behav. 76, 217–236 (2008).
Bialek, W., Cavagna, A., Giardina, I., Mora, T., Silvestri, E., Viale, M. & Walczak, A. M. Statistical mechanics for natural flocks of birds. Proc. Natl. Acad. Sci. USA 109, 4786–4791 (2012).
Becco, Ch., Vandewalle, N., Delcourt, J. & Poncin, P. Experimental evidences of a structural and dynamical transition in fish school. Physica A, 367, 487–493 (2006).
Couzin, I. D., Ioannou, C. C., Demirel, G., Gross, T., Torney, C. J., Hartnett, A., Conradt, L., Levin, S. A. & Leonard, N. E. Uninformed individuals promote democratic consensus in animal groups. Science 334, 1578–1580 (2011).
Killen, S. S. Marras, S. Steffensen, J. F. & McKenzie, D. J. Aerobic capacity influences the spatial position of individuals within fish schools. Proc. R. Soc. London B, 2011.
Vicsek, T., Czirók, A., Ben-Jacob, E., Cohen, I. & Shochet, O. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 75, 1226–1229 (1995).
D'Orsogna, M. R., Chuang, Y. L., Bertozzi, A. L. & Chayes, L. S. Self-propelled particles with soft-core interactions: Patterns, stability and collapse. Phys. Rev. Lett. 96, 104302 (2006).
Couzin, I. D., Krause, J., James, R., Ruxton, G. D. & Franks, N. R. Collective memory and spatial sorting in animal groups. J. of Theor. Biol. 218, 1–11 (2002).
Topaz, C., Bertozzi, A. & Lewis, M. A nonlocal continuum model for biological aggregation. B. Math. Biol. 68, 1601–1623 (2006).
Mecholsky, N. A., Ott, E. & Antonsen, T. M. Obstacle and predator avoidance in a model for flocking. Physica D 239, 988–996 (2010).
Edelstein-Keshet, L., Watmough, J. & Grünbaum, D. Do travelling band solutions describe cohesive swarms? An investigation for migratory locusts. J. Math. Biol. 36, 515–549 (1998).
Grégoire, G., Chaté, H. & Yuhai, T. Moving and staying together without a leader. Physica D 181, 157–170 (2003).
Parrish, J. K. & Edelstein-Keshet, L. Complexity, pattern and evolutionary trade-offs in animal aggregation. Science 284, 99–101 (1999).
Sumpter, D. J. T. The principles of collective animal behaviour. Phil. Trans. R. Soc. London B 361, 5–22 (2006).
Sinclair, A. R. E. The African buffalo: A case study of resource limitation of populations. University of Chicago Press, Chicago, (1977).
Lukeman, R., Li, Y.-X. & Edelstein-Keshet, L. Inferring individual rules from collective behavior. Proc. Natl. Acad. Sci. USA 107, 12576–12580 (2010).
Okubo, A. & Chiang, H. C. An analysis of the kinematics of swarming of Anarete pritchardi kim (Diptera: Cecidomyiidae). Res. Popul. Ecol. 16, 1–42 (1974).
Okubo, A., Chiang, H. C. & Ebbesmeyer, C. C. Acceleration field of individual midges, Anarete pritchardi (Diptera: Cecidomyiidae), within a swarm. Can. Entomol. 109, 149–156 (1977).
Nagy, M., Akos, Z., Biro, D. & Vicsek, T. Hierarchical group dynamics in pigeon flocks. Nature 464, 890–893 (2010).
Katz, Y., Tunstrøm, K., Ioannou, C. C., Huepe, C. & Couzin, I. D. Inferring the structure and dynamics of interactions in schooling fish. Proc. Natl. Acad. Sci. USA 108, 18720–18725 (2011).
Herbert-Read, J. E., Perna, A., Mann, R. P., Schaerf, T. M., Sumpter, D. J. T. & Ward, A. J. W. Inferring the rules of interaction of shoaling fish. Proc. Natl. Acad. Sci. USA 108, 18726–18731 (2011).
Butail, S., Manoukis, N., Diallo, M., Ribeiro, J. M., Lehmann, T. & Paley, D. A. Reconstructing the flight kinematics of swarming and mating in wild mosquitoes. J. R. Soc. Interface 9(75), 2624–2638 (2012).
Ballerini, M., Cabibbo, N., Candelier, R., Cavagna, A., Cisbani, E., Giardina, I., Orlandi, A., Parisi, G., Procaccini, A., Viale, M. & Zdravkovic, V. Empirical investigation of starling flocks: a benchmark study in collective animal behaviour. Anim. Behav. 76, 201–215 (2008).
Ballerini, M., Cabibbo, N., Candelier, R., Cavagna, A., Cisbani, E., Giardina, I., Lecomte, V., Orlandi, A., Parisi, G., Procaccini, A., Viale, M. & Zdravkovic, V. Interaction ruling animal collective behavior depends on topological rather than metric distance: Evidence from a field study. Proc. Natl. Acad. Sci. USA 105, 1232–1237 (2008).
Cavagna, A., Cimarelli, A., Giardina, I., Parisi, G., Santagati, R., Stefanini, F. & Viale, M. Scale-free correlations in starling flocks. Proc. Natl. Acad. Sci. USA 107, 11865–11870 (2010).
Toschi, F. & Bodenschatz, E. Lagrangian properties of particles in turbulence. Annu. Rev. Fluid Mech. 41, 375–404 (2009).
Credland, P. F. A new method for establishing a permanent laboratory culture of Chironomus riparius Meigen (Diptera: Chironomidae). Freshwater Biol. 3, 45–51 (1973).
McCahon, C. P. & Pascoe, D. Culture techniques for three freshwater macroinvertebrate species and their use in toxicity tests. Chemosphere 17, 2471–2480 (1988).
Péry, A. R. R., Mons, R. & Garric, J. Chironomus riparius solid-phase assay. In Blaise C. and Férard J.-F., editors, Small-scale freshwater toxicity investigations volume 1, chapter 8, pages 437–451. Springer, Dordrecht, The Netherlands (2005).
Caspary, V. G. & Downe, A. E. R. Swarming and mating of Chironomus riparius (Diptera: Chironomidae). Can. Entomol. 103, 444–448 (1971).
Downe, A. E. R. & Caspary, V. G. The swarming behaviour of Chironomus riparius (Diptera: Chironomidae) in the laboratory. Can. Entomol. 105, 165–171 (1973).
Ouellette, N. T., Xu, H. & Bodenschatz, E. A quantitative study of three-dimensional Lagrangian particle tracking algorithms. Exp. Fluids 40, 301–313 (2006).
Cavagna, A., Giardina, I., Orlandi, A., Parisi, G. & Procaccini, A. The STARFLAG handbook on collective animal behaviour: 2. Three-dimensional analysis. Anim. Behav. 76, 237–248 (2008).
Rayner, J. M. V., Viscardi, P. W., Ward, S. & Speakman, J. R. Aerodynamics and energetics of intermittent flight in birds. Am. Zool. 41, 188–204 (2001).
Olafsen, J. S. & Urbach, J. S. Velocity distributions and density fluctuations in a granular gas. Phys. Rev. E 60, R2468–R2471 (1999).
La Porta, A., Voth, G. A., Crawford, A. M., Alexander, J. & Bodenschatz, E. Fluid particle accelerations in fully developed turbulence. Nature 409, 1017–1019 (2001).
Ouellette, N. T., O'Malley, P. J. J. & Gollub, J. P. Transport of finite-sized particles in chaotic flow. Phys. Rev. Lett. 101(17), 174504 (2008).
Grünbaum, D., Viscido, S. & Parrish, J. Extracting interactive control algorithms from group dynamics of schooling fish. In Kumar V., Leonard N. and Morse A., editors, Cooperative Control, volume 309 of Lecture Notes in Control and Information Sciences, pages 447–450. Springer Berlin/Heidelberg (2005).
Nouvellet, P., Bacon, J. P. & Waxman, D. Fundamental insights into the random movement of animals from a single distance-related statistic. Am. Nat. 174(4), 506–514 (2009).
Tsai, R. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses. IEEE J. Robot. Autom. 3, 323–344 (1987).
Ouellette, N. T., Xu, H., Bourgoin, M. & Bodenschatz, E. An experimental study of turbulent relative dispersion models. New J. Phys. 8, 109 (2006).
Kelley, D. H. & Ouellette, N. T. Using particle tracking to measure flow instabilities in an undergraduate laboratory experiment. Am. J. Phys. 79, 267–273 (2011).
Ouellette, N. T. & Gollub, J. P. Curvature fields, topology and the dynamics of spatiotemporal chaos. Phys. Rev. Lett. 99(19), 194502 (2007).
Mordant, N., Crawford, A. M. & Bodenschatz, E. Experimental Lagrangian acceleration probability density function measurement. Physica D 193, 245–251 (2004).
Ouellette, N. T., Xu, H. & Bodenschatz, E. Measuring Lagrangian statistics in intense turbulence. In Tropea C., Yarin A. L. and Foss J. F., editors, Springer Handbook of Experimental Fluid Mechanics. Springer-Verlag, Berlin (2007).
Acknowledgements
We are grateful for fruitful discussions with J. E. Brown, K. Burke, A. de Chaumont Quitry, E. R. Dufresne, N. Khurana, L. Odhner, P. Poirier, B. L. Weiss and E. L. Westerman. This work was partially supported by the Army Research Office under grant no. W911Nf-12-1-0517.
Author information
Authors and Affiliations
Contributions
N.T.O. conceived the project. D.H.K. established the midge colony and gathered and analysed the data. Both authors discussed methods, results and analysis and both authors wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Sample tracks
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Kelley, D., Ouellette, N. Emergent dynamics of laboratory insect swarms. Sci Rep 3, 1073 (2013). https://doi.org/10.1038/srep01073
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01073
This article is cited by
-
Flow interactions lead to self-organized flight formations disrupted by self-amplifying waves
Nature Communications (2024)
-
Characterization of lab-based swarms of Anopheles gambiae mosquitoes using 3D-video tracking
Scientific Reports (2023)
-
An equation of state for insect swarms
Scientific Reports (2021)
-
SOUL: data sharing for robot swarms
Autonomous Robots (2020)
-
Three-dimensional time-resolved trajectories from laboratory insect swarms
Scientific Data (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.