Fast and accurate low-dimensional reduction of biophysically detailed neuron models

Abstract

Realistic modeling of neurons are quite successful in complementing traditional experimental techniques. However, their networks require a computational power beyond the capabilities of current supercomputers and the methods used so far to reduce their complexity do not take into account the key features of the cells nor critical physiological properties. Here we introduce a new, automatic and fast method to map realistic neurons into equivalent reduced models running up to > 40 times faster while maintaining a very high accuracy of the membrane potential dynamics during synaptic inputs and a direct link with experimental observables. The mapping of arbitrary sets of synaptic inputs, without additional fine tuning, would also allow the convenient and efficient implementation of a new generation of large-scale simulations of brain regions reproducing the biological variability observed in real neurons, with unprecedented advances to understand higher brain functions.

Introduction

It is becoming more and more evident that a much better understanding of the mechanisms underlying higher brain functions and dysfunctions can be obtained by complementing traditional experimental techniques with modeling methods using realistic, biophysically accurate implementations of neurons and networks as in the Blue Brain Project¹. This approach has been shown to be quite successful in supporting and explaining several experimental findings on, for example, the functional connectivity of neocortical circuits² or the network mechanisms underlying epileptic conditions³. However, the amount of processing power needed to use it in a network able to capture and reproduce the essential aspects of brain functions is beyond the capabilities of current supercomputer systems. Alternatively, quite debated⁴ approaches using extremely simplified phenomenological neurons appear to be too divorced from the real systems, as many fundamental cell properties (such as non uniform distribution of active ion channels) and mechanisms (such as dendritic signal processing) are simply ignored or assumed. For these reasons, the reduction of morphologically accurate neuron models into more tractable units, without loosing important features of their complex dynamics, is quickly becoming a major problem in Computational Neuroscience.

Recently, there have been several attempts to implement a suitable reduction method for conductance-based neurons⁵ to allow neuronal systems to run with reasonable computing requirements while maintaining a direct connection with experimental findings at all integration levels. To reach this goal, several reduction methods have been proposed; for example maintaining the electrotonic properties of the full model by preserving the axial resistance^6,7, the total surface area and somatic input resistance^8,9,10, or the original path resistance between the soma and a single spine¹¹. These kind of methods do not explicitly take into account key features of a neuron, such as synaptic inputs or non uniform distribution of ionic conductances. Furthermore, it has been shown¹² that for branched neurons in the presence of dendritic synaptic inputs these methods do not provide significant accuracy or reduction in the number of compartments and hence in computing time. On the other hand, more general reduction methods using the iterative rational Krylov algorithm^13,14 or a Direct Empirical Interpolation Method¹⁵, have been proposed. While some of these methods are able to take into account the spatial distribution of synaptic inputs and active currents and seem to give accurate results, the reduction procedures do not preserve any direct neurophysiologic interpretation, thus severely limiting their utility. Most importantly, however, all of these methods require fitting parameters that must be obtained for each cell through optimization techniques and fine tuning procedures that are usually computationally exhaustive.

In this paper, we introduce a new, automatic and fast method to simplify models of complex neurons with an arbitrary distribution of active properties, synaptic inputs and dendritic trees. Using suitable key properties of a homogeneous population of neurons to set up the reduction algorithm, the method is able to transform any morphologically and biophysically accurate neuron into an equivalently reduced model that can run up to > 40 times faster. Furthermore, by mapping arbitrary sets of synaptic inputs without additional fine tuning, the method would also allow a convenient and efficient implementation of large-scale networks reproducing the biological variability observed in real neurons.

Results

The method is schematically illustrated in Fig. 1a and described in details in the Methods section. To implement and test it, we used 17 realistic models of hippocampal CA1 pyramidal neurons (from ref. 16), based on 3D reconstructions available on the public http://neuromorpho.org database. A typical neuron including a random group of excitatory synapses is shown in Fig. 1a (left). As a preliminary step, we noted that the morphology and distribution of active properties for these cells¹⁷ allowed us to define nine functional regions (clusters) composed by a variable number of dendritic compartments, indicated with different colors in Fig. 1a . The first step in the reduction algorithm ( Fig. 1a , middle) is to map each cluster into an equivalent single compartment. This is carried out by using merging rules based only on the passive, active and morphological properties of the full neuron without any fitting or tuning procedure. The synaptic and ion channels peak conductances are then rescaled and synapses are mapped to appropriate locations in the equivalent model. The scaling of the peak conductances is the only step in which an explicit set of simulations must be preliminarily carried out with the full model to find the critical input strength (the max Stim parameter, see Methods) for which a particular neuron reaches a depolarization block state¹⁸. It should be stressed, however, that this is a peculiar condition of this cell population with enough functional importance to be included into the reduced model¹⁸. Typical results are shown in Fig. 1b , where we compare the somatic membrane potential of the full model and its reduced version in response to an identical train of 140 or 420 synaptic inputs with random peak conductance, spatial distribution and activation (see Methods). The good agreement between the two models is demonstrated by the average results reported in Fig. 1c , as a function of the number of synaptic inputs, in terms of the number of action potentials (APs) and the interspike distribution (ISI) obtained from 10 simulations using random redistributions of peak conductance, spatial location and activation frequency of all synapses without any parameters tuning. These results show that the method is able to map a detailed realistic neuron into a reduced version that quantitatively reproduces the firing properties of the full model.

Figure 1

A method to reduce the computational complexity of realistic models of neurons.

(a) (left) typical 3D reconstruction of a realistic hippocampal CA1 pyramidal neuron (cell c70863 from the neuromorpho.org public archive), composed by 843 membrane segments; red circles indicate synapses location; different colors for dendrites highlight the different clusters used for this kind of cell population; (middle) Flow-chart illustrating the main steps to reduce a morphologically and biophysically detailed neuron model into a reduced, but functionally equivalent, version; (right) schematic representation of the equivalent model (27 membrane segments) obtained after application of the reduction method. (b) Somatic membrane potential of the full (black traces) and the reduced (red traces) model during a simulation activating 140 (left) or 420 (right) synapses. (c) (left) Average (n = 10, ±sd) number of APs elicited in 500 ms long simulations as a function of the number of synaptic inputs activated in the original (black) or in the reduced (red) model; the two curves are statistically indistinguishable (Wilcoxon Signed Rank test, p = 0.879); (right) normalized InterSpike Interval (ISI) distribution, from 10 simulations of the original (black) or the reduced (red) model during a simulation activating 140 synapses; the two curves are statistically indistinguishable (Wilcoxon Signed Rank Sum test, p = 0.626).

To evaluate the firing behavior of the reduced models, for all neurons used in this work we compared the somatic APs and ISIs obtained during all simulations with those obtained in the full models under the same conditions. It should be noted that, given the high variability observed in experimental recordings from the same neuron in response to multiple instances of the same stimulus¹⁹, the main aim of the method was not to obtain identical traces but to build a reduced model able to reproduce the same average I/O properties, i.e., APs and ISIs, generated by a number of synaptic inputs randomly located on a specific neuron. Thus, a rigorous comparison of the somatic voltage trajectories was not appropriate. However, we tested and confirmed that the average number of APs and ISI values obtained in the group of accurate neurons within the physiological range of input (i.e., below the depolarization block state for most neurons, up to 200 synapses in our case) were statistically indistinguishable from those obtained in the reduced models (Wilcoxon Signed Rank test, p = 0.553 for APs and p = 0.232 for ISIs). Above this range, the statistics was biased by the large variability (in both the full and reduced model) caused by the complex spiking dynamics of these neurons when they are close to the depolarization block state¹⁸.

For a more appropriate evaluation of the differences over the entire range, we tested whether the reduced neuron was able to correctly identify the presence (or absence) of a spike within a given time interval (see Fig. 2a and Methods). An accuracy factor was calculated as:

where TP (True Positives), is the number of spikes from the morphological neuron that are also found in the reduced model; TN (True Negatives) is the number of intervals in which the neuron does not fire a spike in both the morphological and the reduced model; FP (False Positives) is the number of mismatched spikes in the reduced model; FN (False Negatives) is the number of spikes in the morphological neuron that are not matched in the reduced model. An accuracy value of 1 represents the ideal case of a perfect correspondence of spikes and silent periods between the full and the reduced model. In Fig. 2b we plot the average accuracy (from 10 simulations) for cell c70863 as a function of the number of synaptic inputs ( Fig. 2b , black). As can be seen, it is quite high over the entire input range tested. However, physiological processes can result in some variability in the ion channels peak conductance and excitability properties for individual neurons, even if they belong to the same cell population. To test the robustness of the method, we thus ran additional simulations ( Fig. 2b , red and blue) with random perturbations of the peak channel conductances and the critical input (max Stim) used to implement the reduced model. We stress that all simulations were carried out automatically, using only the input data without any tuning or fitting procedure. The results demonstrate that the method is quite robust and able to maintain very good accuracy even in those cases where model parameters are not precisely defined.

Figure 2

The method is accurate and robust to fluctuations of model parameters.

(a) Schematic representation of accuracy calculation in a typical case (cell cd1152); somatic traces obtained from simulations of the full (black) and reduced (red) model were scanned to test for mismatch of spikes or silent periods occurring within a variable time window (see Methods); light green: True Positive; dark green: True Negative; light pink: False Positive; dark pink: False Negative; Accuracy = 0.9; (b) accuracy of the reduced model for cell c70863 as a function of the number of active synaptic inputs using the original set of the full model parameters (black) and average accuracy (n = 10) for ±25% or ±20% random fluctuations in peak channels conductance (red) or in the critical input max Stim (blue), respectively.

We next tested the overall accuracy obtained for all the 17 morphologies used in this work and its robustness against changes in the parameters used to calculate it, i.e., α and τ (see Methods). The results presented in Fig. 3a and in Fig. 3b for each cell, demonstrate a very good average accuracy over the entire input range, with a relatively large variability around the critical input region, where there is a drastic change of the firing regime caused by the depolarization block¹⁸.

Figure 3

The method is accurate for different morphologies.

(a) Average accuracy (n = 17, ±sd) obtained for the reduced models of all morphologies as a function of the number of active synaptic inputs; (b) average accuracy for the reduced model of each morphology, from 260 simulations using a different number of synaptic inputs with random spatial redistribution, activation times and peak conductance; (c) average accuracy for 10, 140 and 340 synaptic inputs as a function of the simulation length; in all cases, α = 0.35 and τ = 10 ms; (d) average accuracy (n = 170) obtained for the reduced models of all morphologies from 500 ms long simulations with 10, 140 and 340 synaptic inputs as a function of τ (black plots, α = 0.35) and as a function of α (gray plots, τ = 10 ms).

Since the accuracy is a probability measure within a given time interval, its value may depend on the number of events occurring during simulations of different length. For all calculations we used 500 ms long simulations. To test if this was enough to avoid systematic errors, we calculated the accuracy as a function of the simulation length for three representative cases:

• 1 10 synapses, to test conditions close to subthreshold activity,

• 2 140 synapses, well within the regularly firing regime for all neurons and

• 3 340 synapses, a condition for which all neurons will reach a depolarization block state.

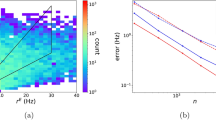
The results, presented in Fig. 3c , demonstrate that the average accuracy values obtained from simulations of different length (180–500 ms) are quite robust over the entire input range. The α and τ parameters set the width of the time window used to calculate the accuracy (see Methods). They thus determine the relative precision needed to define an event as True Positive/Negative or False Positive/Negative in comparing the somatic traces obtained using the full and the reduced model. In general, large values may result in the accuracy being biased toward very high or very low values, whereas very small values will require a perfect match between the traces. As discussed before, here we were not interested in a perfect match of voltage trajectories. In all cases we used α = 0.35 and τ = 10 ms (i.e., a maximum time window of 7 ms, see Methods). To test if this choice was appropriate we repeated the accuracy calculations for 10, 140 and 340 synapses, using different combinations of α and τ around these values. As shown in Fig. 3d the accuracy was quite robust to significant changes in either parameter. The only exception was the low accuracy obtained for α = 0.2 and a strong stimulation (140 synapses, Fig. 3d , gray triangles). This result can be explained by considering that, under these conditions, the largest time window was only ≈ 1.4 ms. The run times for the reduced models were, 13–50 times faster (at a confidence level of 95%) than the corresponding full models ( Fig. 4 , gray), with setup times (i.e., the time required to map an accurate morphology and its synaptic inputs into a reduced version ready to run) of 0.2–0.3 s, less than ≈ 0.5% of the average runtime of the full model and orders of magnitude faster than the current optimization procedures. Taken together, these results demonstrate that our method is fast to apply and able to map a biophysically detailed neuron into a very accurate reduced version running much faster than the original model.

Figure 4

The method greatly reduces the run time.

(black) Average runtime for a 500 ms simulation, as a function of the number of active synaptic inputs (α = 0.35, τ = 10 ms), for the original models (circles) and their reduced version (triangles). (gray) Average run time reduction (error bars represent 95% confidence interval).

Discussion

The reduction of a neuron model's complexity, without losing the fundamental properties of a biophysically accurate implementation, especially synaptic inputs, is a major obstacle to understand the cellular mechanisms of higher brain functions and dysfunctions through large-scale network models closely related to experimental data. The modeling of neurons properties starts with the fundamental works by Rall^20,21 and continued with several reduced models proposed to represent the intrinsic electrophysiological properties of a neuron population. A few of the most representative examples in this field are those for hippocampal CA3 pyramidal neurons, implemented with models of two²² or nineteen compartments²³. Along the same line were the models of neurons in the olfactory bulb²⁴ and in the Dentate Gyrus²⁵. The main aim in these cases was to implement a physiologically reasonable subset of properties for neurons belonging to a given population, without any reference to specific cells. This is different from the main aim of this work, which focuses on individual cells. We were interested in reducing the complexity of an existing biophysically accurate model of individual cells. The rationale for this approach is that the intrinsic properties of each neuron are the result of cell-specific activity dependent changes²⁶. These changes may represent a unique synaptic input history and form the basis for the immense computational power of single neurons²⁶. It is thus important to preserve these properties in implementing reduced models of individual cells to be used in large networks. None of the previously published reduction methods is able to take into account this aspect in a fast and accurate way, since they are either not designed to include synaptic inputs or active dendritic conductances, or require prohibitively long and rather specialized optimization and fine tuning procedures for each cell. With our method, an arbitrary number of neurons of a given population can be efficiently and accurately mapped, in a negligible time, into much smaller equivalent units that maintain all critical cellular and synaptic properties, allowing a direct comparison with experimental findings. In particular, it is the mapping of arbitrary synaptic inputs without any additional tuning that makes our method to stand out from all previously published reduction methods. This will allow the convenient and efficient implementation of a new generation of large-scale simulations of brain regions reproducing the biological variability observed in real neurons, with unprecedented advances to understand higher brain functions.

Methods

Computational details

All simulations were implemented using v7.0 of the NEURON simulation environment²⁷. The model and simulation files are available for public download under the ModelDB section (acc.n. 146376) of the Senselab database (http://senselab.med.yale.edu). To ensure a representative range of morphological properties, we used 17 3D reconstructions of CA1 neurons from young (about 6 wk old) rats available on the public archive www.neuromorpho.org. One of the morphologies was used to setup the method, 16 to test its accuracy. The set of passive properties, voltage-dependent ionic channels, kinetic and distribution were identical to those in ref. 16 (ModelDB acc.n. 55035). In this model, already validated against a number of different experimental findings on electrophysiological and synaptic integration properties of CA1 neurons^28,29, sodium and DR-type potassium conductances were uniformly distributed throughout the dendrites, whereas A-type Potassium and I_h conductances were linearly increasing with distance from soma.

To simulate a generic background excitatory synaptic activity, a variable number of excitatory synapses were modeled as a double exponential conductance change with 0.4 and 0.6 ms for rise and decay time, respectively, consistent with single EPSC currents at physiological temperature³⁰. They were randomly distributed in the apical dendrites 10–500 µm from the soma, with peak conductance drawn from a Gaussian distribution of 2 ± 1 nS. Each synapse was independently and randomly (Poisson) activated at a frequency in the gamma range (40–80 Hz), which is an ubiquitous rhythm of neuronal population³¹ and involved in memory encoding and retrieval processes³².

Merging rules and scaling of ionic and synaptic conductances

As preliminary step, we considered experimental findings on the morphology and the electrophysiological properties of the neuron population that we were interested to study (i.e., CA1 pyramidal neurons, reviewed in ref. 17) and the specific biophysically accurate model that we used as reference¹⁶. They suggest that these neurons have different functional regions, that we empirically identified in the following finite set of clusters:

cluster 0: soma;

cluster 1: axon;

cluster 2: apical trunk at distance d ≤ 100 µm from soma;

cluster 3: apical trunk at distance d > 100 µm from soma;

cluster 4: apical dendrites (oblique) at distance d ≤ 100 µm from soma;

cluster 5: apical dendrites (oblique) at distance d : 100 µm < d ≤ 300 µm from soma;

cluster 6: apical dendrites (distal) at distance d > 300 µm from soma;

cluster 7: basal dendrites (proximal) at distance d ≤ 100 µm from soma;

cluster 8: basal dendrites (distal) at distance d > 100 µm from soma.

The second step is to map each functional region into a single compartment in the reduced model and calculate its morphological and passive properties. Following Destexhe et al. (1998)⁹ and Bush & Sejnowski (1993)⁷, the length of the compartment equivalent to a given cluster is chosen as the sum of the dendrites' length if the dendrites are sequential (seq) or as the average length weighted by their respective areas if the dendrites are branched (br), i.e.,

where L_i and S_i are the lengths and the areas of the i–th dendrite, respectively. Then, we obtain

The diameter of the equivalent compartment is chosen taking into account the axial resistance of the ensemble of dendritic segments it represents

where

and R_a is the specific axial resistance of each dendrite in the cluster and r_a,i is the axial resistance of the i–th dendrite.

Moreover, in our method we set

where H is the total number of the dendrites in the cluster and is the specific axial resistance in the equivalent compartment.

In the above merging rules, the membrane area and the axial resistance of the neuron are not conserved and this modifies the electrotonic properties of the equivalent neuron. To account for these differences, a set of scaling factors is usually applied to ionic and synaptic conductances and passive properties. Current reduction methods find an appropriate set of scaling factor through a fine tuning procedure for the passive and active models using a somatic current injection^7,9,11 and they do not thus take into account the input-output properties of the detailed model in response to synaptic stimulations.

In our method, for each cluster we determine a scaling factor, , which depends on the presence of synaptic inputs as follows:

where S^eq is the surface area of the equivalent compartment and w_i = 1 if in the i–th dendrite there is at least one synapse and 0 otherwise. This factor, which thus depends on the spatial distribution of synapses, is used to calculate the scaled values for the specific membrane capacitance, the specific membrane resistance and ion channels peak conductance

The reduced model will thus follow any specific spatial distribution of the peak conductances of the full neuron.

It should be stressed that the above parameters are calculated directly from the full model properties without any fitting or parameter tuning procedure.

Mapping synaptic inputs location

The most challenging aim of our paper was to build an accurate reduction technique taking into account the effect of synaptic inputs. This is the primary and the most difficult mechanism to preserve for an accurate reduction procedure. In this work, we hypothesized that this problem could be solved by rescaling (and repositioning) the synaptic conductances in such a way to maintain the same signal propagation as in the full model. We found that a good way to achieve this goal was to take into account the axial path resistance. To this purpose, synapses were repositioned in the equivalent model according to the following procedure. Let's consider synapse i on cluster C of the full model. We define the axial path resistance, r_i,PATH, as

where r_a,h is the axial resistance of the h–th segment of the path consisting of the unique sequence of j segments leading from the soma to the dendrite on which the synapse is positioned.

Let r_max and r_min be the maximum and the minimum axial path resistance of cluster C, i.e.,

where r_PATH indicates the axial path resistance of a given dendrite belonging to cluster C.

Each cluster C of the full model is modeled with a single compartment (C′) in the reduced model. To define the number of membrane segments, n′, composing each cluster C′ we used³³

where

d_λ = 0.1 and f can be used as a parameter to adjust the number of C′ membrane segments. Owing to Eq.(6), the number of segments, n′, of the equivalent compartment C′ is a function of the number and spatial distribution of the synapses, through .

We found that f = 3 gave the best compromise between a high reduction factor in the total number of segments (which reduces computing time) and a better signal propagation (which increases the accuracy). The average reduction factor, i.e., the ratio between the total number of segments in the morphological and reduced models and accuracy for a few values of f are reported in Supplementary Fig. 1 .

The next aim is to find the most appropriate segment of C′ to place the i–th synapse. To this purpose, we define

where k represents the number of segments from the soma to compartment C′ and the axial resistance of the h–th segment of C′.

The C′ segment where the i–th synapse will be placed is defined by its axial path resistance in such a way to fulfill the relation

In other words, equation (7) identifies the segment s_i of C′ in such a way that

Finally, the peak synaptic conductance is scaled as

where g_i,max is the original peak conductance of the i–th synapse of the full neuron and is a scaling factor defined as

where N_syn is the total number of synapses, the 0.75 and 0.6 exponents depend on the type of neuron population to model and max Stim represents the number of synapses above which the neuron reaches the depolarization block state¹⁸. This is the only place where a preliminary set of simulations with an increasing number of activated synapses is needed to better characterize a specific feature of these cells. In Table 1 we report the max Stim value for all the morphologies used in this work. The computing time per cell to find this value was approximately 15 min, on the same system used for all simulations (Intel Xeon 2.93GHz, 4 core).

Table 1

Accuracy calculation

For any given morphology, the overall quality of the reduction was calculated by comparing 260 simulations (26 sets of increasing number of synapses, each repeated 10 times with random spatial distribution, activation times and peak conductance). The accuracy factor was calculated as:

where TP (True Positives), is the number of spikes from the morphological neuron that are also found in the reduced model; TN (True Negatives) is the number of intervals in which the neuron does not fire a spike in both the morphological and the reduced model; FP (False Positives) is the number of mismatched spikes in the reduced model; FN (False Negatives) is the number of spikes from the morphological neuron that are not matched in the reduced model.

For any spike in the full model at time t_i, TP, FP and FN are calculated by exploring the behavior of the reduced model in the interval

in such a way that

Unless noted of otherwise in all simulations we used α = 0.35 and the maximum semiamplitude of any interval Δt_i was set as

Finally, TN is calculated in the interval (no activity in the full model) in such a way that TN is equal to the number of subintervals of , of amplitude τ = 10 ms, without any spike in the reduced model.